黏弹性三参数地基梁横向自由振动

彭 丽， 丁 虎， 陈立群,3

(1. 上海大学 上海市应用数学和力学研究所，上海 200072；2. 上海师范大学 建筑工程学院，上海 201418；3. 上海大学 力学系，上海 200444)

弹性地基梁作为很多工程元件的模型，如公路、跑道、铁路、输油管道等，其振动特性一直是科学以及工程应用中广受关注的问题[1-3]。

Wang等[4]通过分离变量方法研究了多种经典边界下的横向振动固有频率，研究发现，计入了剪切模量影响的Pasternak型基础梁的频率要大于Winkler基础梁的频率。Tsiatas[5]通过线性加立方非线性刚度的地基梁响应，比较了Pasternak地基梁模型和Winkler地基梁模型，研究发现，梁的响应对Pasternak地基参数非常敏感。上述研究均基于弹性基础梁并未考虑工程实际中的阻尼因素的影响。ÇalIm[6]通过无限长黏弹性Pasternak地基梁模型，研究了集中脉冲激励下基础梁的动力学响应，发现地基中的黏性影响显著。截至目前，对于有限长黏弹性Pasternak地基梁模型的研究工作还很少，且已有的研究方法主要局限于采用假设模态的Galerkin截断或者有限元仿真等数值方法分析，缺少解析或者近似解析的研究工作。复模态解析方法可有效解决黏弹性系统的振动问题，在有阻尼离散系统和连续系统振动问题中应用已较广泛[7-9]。本文将该解析方法推广至地基梁的研究，分析不同边界条件的黏弹性Pasternak地基梁的横向自由振动特性。

本文将复模态方法推广至地基梁系统的振动分析中。运用复模态方法近似分析黏弹性Pasternak地基梁在不同边界条件下的振动特性。通过具体算例，分析了刚度、黏性系数等对固有频率和模态函数的影响。但复模态方法得到的频率方程是以超越方程形式表达的，需要通过数值方法求解，其精度也需要进一步验证。微分求积法作为一种数值求解方法，已成功应用于连续梁的振动特性数值分析，计算结果表明，这种方法具有明显的高精度和低耗时[10-11]。本文用微分求积法得到的数值解验证了复模态的近似解析解。

1 振动控制方程

黏弹性Pasternak地基梁的物理模型如图1所示。

其振动控制方程为：

(1)

式中：ρA为单位长度梁的质量，EI为梁的刚度，k1为弹性模量，k2为剪切模量，c为地基黏性系数。

图1 黏弹性Pasternak地基梁模型

取无量纲化变量和参数

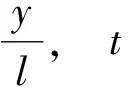
(2)

式中:l和ρ分别表示地基梁的长度和密度，x和t分别表示空间和时间坐标。kf、k1、k2和c分别为无量纲后对应的刚度系数,弹性系数，剪切系数和黏性系数。

无量纲化后的振动控制方程为

(3)

2 复模态近似分析

对于黏弹性Pasternak地基梁，设

(4)

其中,λn=-δn+iωn，(n=1,2,3,…)，δn是衰减系数，ωn是振动频率。将(4)式代入控制方程(3)，得到:

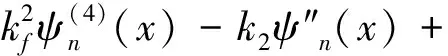
(5)

利用指数形式特解

ψn(x)=eγnx

(6)

代入方程(5)后，导出本征方程

(7)

4个本征值为

(8)

因此，方程(5)的通解可写作

ψn(x)=C1neγ1nx+C2neγ2nx+C3neγ3nx+C4neγ4nx

(9)

2.1 简固支边界条件下的固有频率和模态函数

考虑梁的一端简支一端固支的边界条件

y(0,t)=y(1,t)=0,
y″(0,t)=y′(1,t)=0

(10)

代入式(4)后，得:

(11)

将式(9)代入式(11)得到:

(12)

根据有非零解的要求，得到的频率方程为超越方程

(13)

式(13)无法得到精确解，必须通过数值方法求解。

由式(12)可得到用C1n表示的Cjn(j=2, 3, 4)，代入(9)式后得到模态函数表达式:

(14)

2.2 固支边界条件下的固有频率和模态函数

考虑两端固支的边界条件：

y(0,t)=y(1,t)=0,y′(0,t)=y′(1,t)=0

(15)

代入式(4)后，得：

(16)

与简固支边界相似，得到频率方程：

(eγ2n-eγ3n)(eγ1n-eγ4n)(-γ2nγ3n-γ1nγ4n)+(eγ1n-eγ3n)(eγ2n-eγ4n)(γ1nγ3n+γ2nγ4n)+

(eγ1n-eγ2n)(eγ3n-eγ4n)(-γ1nγ2n-γ3nγ4n)=0(17)

继而得到模态函数表达式：

(18)

2.3 自由边界条件下的固有频率和模态函数

考虑两端自由的边界条件

y″(0,t)=y″(1,t)=0
y′″(0,t)=y″′(1,t)=0

(19)

代入(4)式后，得

(20)

与前两种边界相似，得到频率方程

(eγ1n-eγ2n)(eγ3n-eγ4n)(-γ1nγ2n-γ3nγ4n)]=0(21)

ω1=0满足方程，因此，自由边界条件下的一阶频率为零。除去一阶频率外，用数值方法求解时，自由和固支两种边界条件下，地基梁有相同的一组频率值，但同一数值，两种边界对应的阶数不同。

与固支边界不同的是，自由边界条件下的模态函数表达式为:

(22)

3 具体算例

对于振动控制方程(2)式，文献[8]中数值无量纲化后，取kf=0.003 5，k1=0.72，k2=0.367，c=0.10，代入频率方程。通过数值方法计算得到前八阶固有频率，如表1中原始参数对应的一组数据所示。自由边界条件下，一阶频率为零，第n阶频率同固支边界的第(n-1)阶频率值。简固边界条件下得到的频率值比固支边界略小，且随着阶数的升高，差值相应略有增加。其他参数不变情况下，黏性系数增大5倍后(c=0.5)对应的频率值，比原始参数对应的频率值略小。说明随着黏性系数的增大，地基梁的频率减小。刚度系数增大5倍后(kf=0.017 5)得到的频率值，比原始参数对应的频率值增大。尤其是第四阶之后，随着阶数的增加，频率值增大的幅度更为明显。说明随着刚度系数的增大，地基梁的频率增大，尤其是高阶频率值增长明显。

不同边界的前四阶模态函数图，分别见图2、图3和图4。由图可见，高阶模态函数的幅值较低阶模态函数幅值小，且实部和虚部关于x轴对称。也证明本文的数值计算误差有限。简固和固支两种边界的模态函数实部和虚部图非常相似。自由边界条件下，一阶频率为零，模态函数表达式的值也为零，故一阶模态图形对应为x轴所在的一条直线。

表1 不同边界条件下，前八阶固有频率

4 微分求积验证

微分求积法(DQ法)是Bellman等根据数值积分思想提出的一种求解偏微分方程的数值方法。其本质是把函数在给定离散点上的各阶导数值，近似地用全域上所有网点处的函数值的加权和来表示。

黏弹性Pasternak地基梁的计算区域为0≤x≤1。x方向的网点数为N。离散点的分布采用非均匀离散点布置，其分布形式为：

(23)

应用微分求积规则，每个网点处对应的函数导数为

(24)

其中权系数的定义为:

(25)

这里，xn(n=i，k，μ)为节点坐标，N为节点总数。

当r= 2，3，…，N-1时，有

(26)

将式(26)代入控制方程式(3)与简固及固支边界条件，得到相应网点的微分求积近似离散:

(27)

其中

yi(t)=y(xi,t)

(28)

简固边界条件下

(29)

固支边界条件下

(30)

通过(27)式，微分求积方法数值计算固有频率可归结为广义本征值问题。选取离散抽样点数N=19。图5、图6给出了不同方法下，具体算例的比较。实线代表复模态分析方法的近似解析结果；黑点线代表微分求积法的数值结果。定量上，微分求积数值解与复模态分析的近似解析解非常接近；在定性上，使用微分求积法和复模态分析得到的固有频率曲线具有相同趋势。由图5可见，不同边界条件下，两种方法所得自由振动固有频率结果吻合的很好。

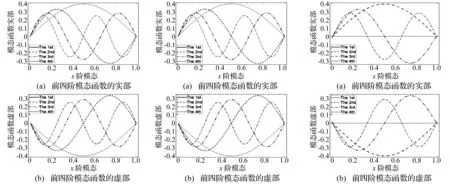
图2 简固边界条件下地基梁的模态函数

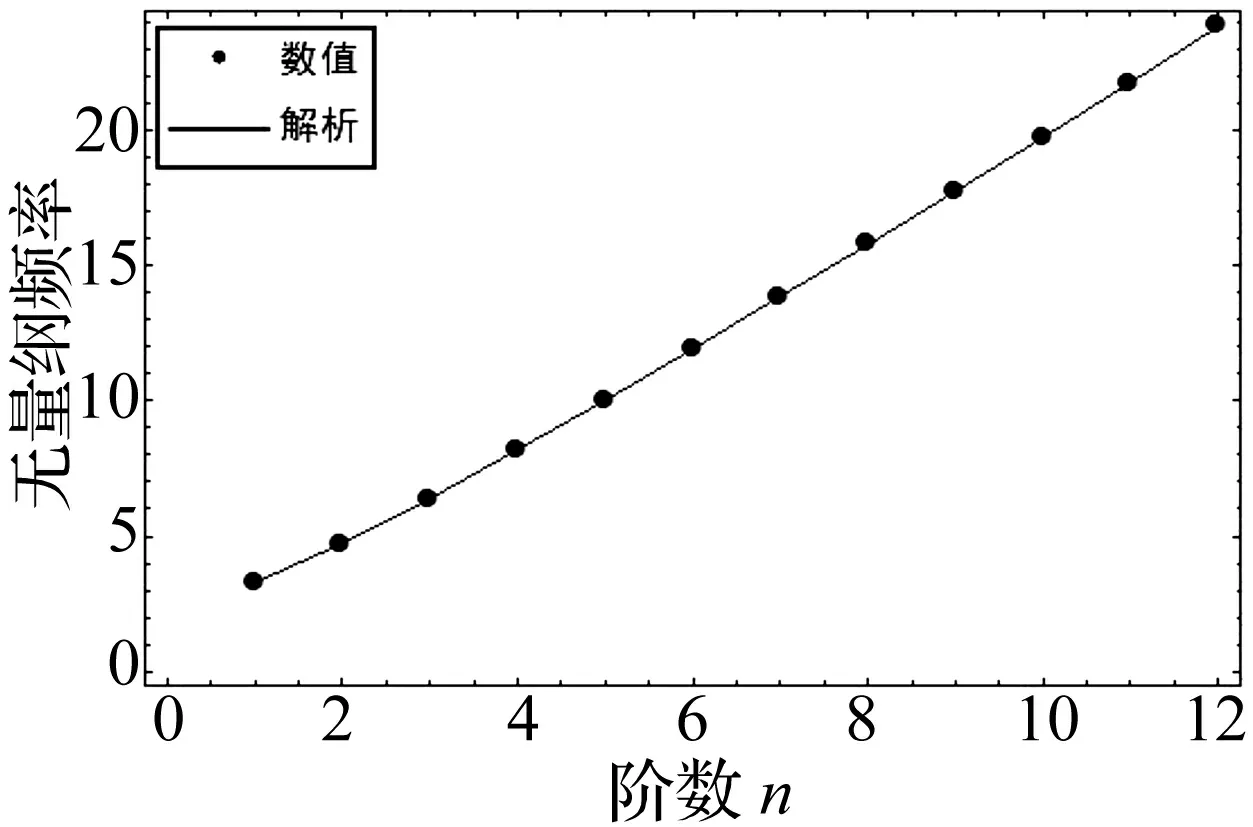
图5 固支边界下数值和解析的比较

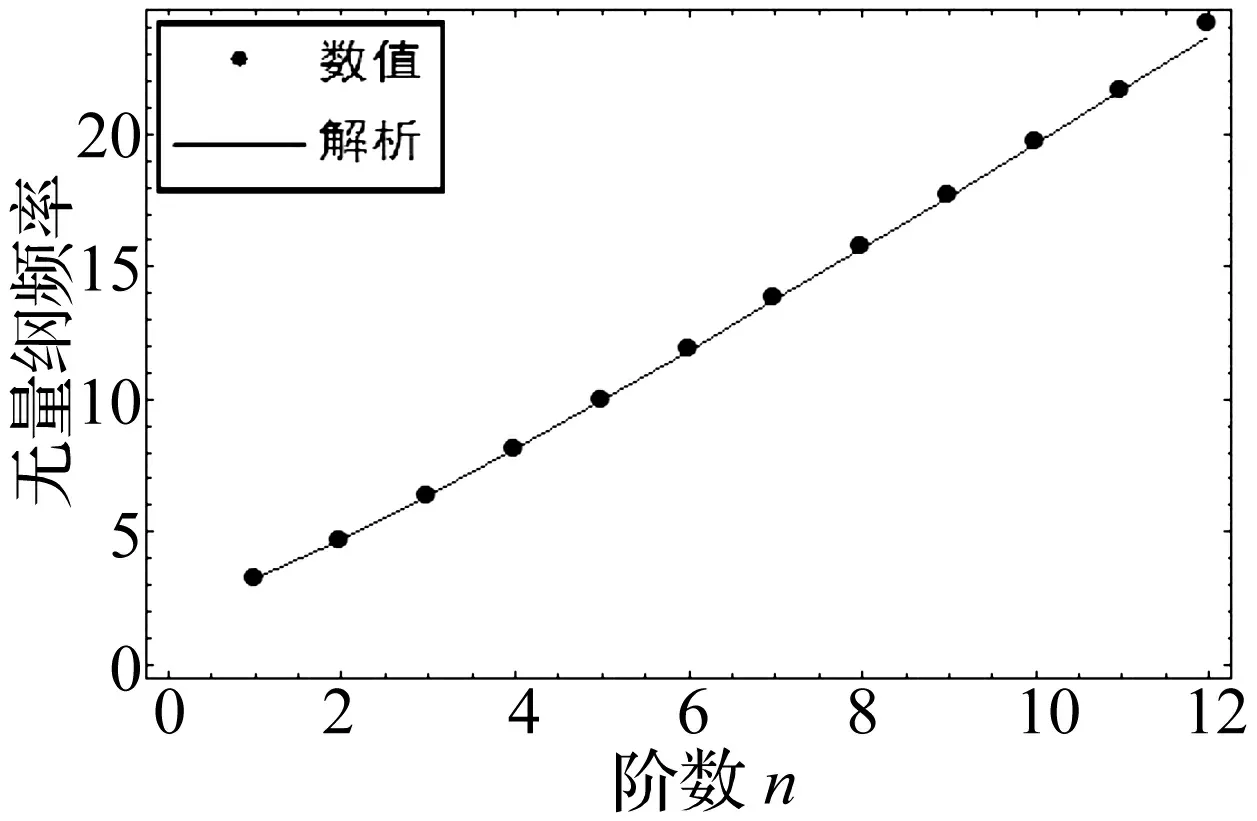
图6 简固边界下数值和解析的比较

5 结 论

本文应用复模态近似分析方法研究Pasternak地基梁的横向自由振动特性，得到不同边界条件下的固有频率和模态函数，并分析了边界条件、刚度系数和地基黏性系数对固有频率的影响。运用微分求积方法得到离散后的控制方程，将微分求积法得到的数值解与复模态方法的近似解析解进行比较。

通过具体算例表明，简固和固支两种边界条件下的振动特性非常接近，简固边界的频率值比固支边界略有降低。两种边界的模态函数图形相似。两端自由边界条件下，一阶频率为零，第n阶频率同两端固支的第n-1阶频率值。随着刚度系数的增大和黏性系数的减小，各阶固有频率均增大。定量上，微分求积数值解与复模态的近似解析解非常接近；在定性上，固有频率的数值解与近似解析解的曲线具有相同趋势。

综合上述，本文证明了复模态方法适用于黏弹性地基梁的横向自由振动分析。为将复模态方法进一步向地基梁振动问题推广奠定基础。

参 考 文 献

[1]李韶华, 杨绍普. 重型汽车与路面的耦合作用研究[J]. 振动与冲击, 2009, 28(6)：155-158.

LI Shao-hua,YANG Shao-pu. Dynamical interaction between heavy vehicle and road pavement [J]. Journal of Vibration and Shock, 2009, 28(6)：155-158.

[2]李皓玉, 杨绍普, 李韶华. 车、路的相互作用下沥青路面动力学特性分析[J]. 振动与冲击, 2009, 28(4)：86-92.

LI Hao-yu, YANG Shao-pu, LI Shao-hua. Dynamical analysis of an asphalt pavement due to vehicle-road interaction [J]. Journal of Vibration and Shock, 2009, 28(4)：86-92.

[3]Ding H, Chen L Q, Yang,S P. Convergence of galerkin truncation for dynamic response of finite beams on nonlinear foundations under a moving load[J]. Journal of Sound and Vibration, 2012, 331(10)：2426-2442.

[4]Wang T M, Stephens J E. Natural frequencies of timoshenko beam on pasternak foundations[J]. Journal of Sound and Vibration, 1977, 51(2)：149-155.

[5]Tsiatas G C. Nonlinear analysis of non-uniform beams on nonlinear elastic foundation[J]. Acta Mechanica, 2010,209(1-2)：141-152.

[6]ÇalIm F F. Dynamic analysis of beams on viscoelastic foundation [J]. European Journal of Mechanics A/Solids, 2009, 28(3)：469-476.

[7]倪金福, 张阿舟. 关于复模态理论的几个问题 [J]. 振动与冲击, 1984,3(1)：15-23.

NI Jin-fu, ZHANG A-zhou. On the Complex Mode Theory[J]. Journal of Vibration and Shock, 1984,3(1)：15-23.

[8]刘 芳, 陈立群. 黏弹性梁弯曲振动的复模态分析 [J]. 机械强度, 2005, 27(5)：586-589.

LIU Fang, CHEN Li-qun. Complex modal analysis of bending vibration of a viscoelastic beam[J]. Journal of Mechanical Strength, 2005, 27(5)：586-589.

[9]Huang W, Zou Y D. The dynamic response of a viscoelastic Winkler foundation-supported elastic beam impacted by a low velocity [J]. Computers & Structures, 1994, 52(3)：431-436.

[10]王 波, 陈立群. 微分求积法处理轴向变速黏弹性梁混杂边界条件 [J]. 振动与冲击, 2012, 31(5):87-91.

WANG Bo, CHEN Li-qun. Treating hybrid boundary condition of an axially accelerating viscoelastic beam via a differential quadrature scheme[J]. Journal of Vibration and Shock, 2012, 31(5)：87-91.

[11]Malik M，Bert C W. Implementing multiple boundary conditions in the dq solution of higher-order pde’s：application to free vibration of plates [J]. International Journal for Numerical Methods in Engineering, 1996, 39(7)：1237-1258.