EMD自适应三角波匹配延拓算法
王录雁,王 强,鲁冬林,张梅军,毛 迪
(解放军理工大学,南京 210007)
Huang等[1]提出了经验模态分解(Empirical Mode Decomposition,EMD)技术,在处理非平稳、非线性信号方面具有独特的自适应性,使其成为近年国内外学者的研究热点。经过多年的研究,EMD技术的理论体系逐渐完善,并已在众多领域得到了实践应用,但其端点效应问题一直制约着该方法的推广应用。解决EMD端点效应主要有两个途径:数据延拓法和改进插值法。其中数据延拓法具有理论简单、效果明显的特点,因而成为主要的研究方向。文献[2]对近年出现的典型的数据延拓算法进行了分类综述,分析了各种方法的特点及不足。其中波形匹配方法[3-8],立足于近端点处波形与内部波形的相似性实现数据延拓,延拓数据不但考虑了近端点处数据的局部变化趋势,同时保留了波形的原始特征,具有其他方法所不可比拟的优势,因而成为遏制EMD端点效应的一个重要研究方向。
波形匹配法的关键步骤之一是波形匹配程度的计算。文献[3,8]及文献[4-7]分别采用了三角波和基于距离的波形匹配算法,在实际应用中尚且存在一些不足,本文在此基础上,提出一种自适应的三角波形匹配延拓算法。
1 EMD方法及其端点效应
1.1 基本原理
EMD方法是将非线性、非平稳的信号分解为有限个具有单一瞬时频率的固有模态函数(Intrinsic mode function,IMF),步骤如下:
(1)确定信号的极值点;
(2)用三次样条曲线对所有极值点进行插值,生成上、下包络线;
(3)计算上下包络线均值m1,求出h1
h1=x(t)-m1
(4)判断h1是否符合IMF判据,如果h1符合IMF判据[1],则h1即为一个IMF;若h1不符合IMF判据,则重复执行步骤(1)~(3),直到h1k=h1(k-1)-m1k符合判据。
(5)分离IMF后重复执行步骤(1)~(4),直到分离出所有的IMF(ci)直到残留项rn不再满足筛分条件[1]为止,则有:
(1)
1.2 端点效应问题
在采用三次样条曲线对极值点进行插值时,由于数据两端端点处数值不能同时既为极大值又为极小值,于是在拟合包络线时,会在端点处失去约束,导致包络线在端点处发生大幅摆动。随着分解的进行,误差就会由端点处逐渐向内传播,严重的情况下会使分解的数据丧失物理意义。如图1所示,在没有采取抑制措施的情况下,包络线在端点处出现了大幅摆动,致使分解结果发生严重偏离,只分解出了两个有意义的频率成分便终止了循环筛分;采用镜像极值延拓法有效遏制了端点效应,获得了三个有效的频率成分。

图1 EMD端点效应问题及端点延拓
2 波形匹配方法
近年来,波形匹配延拓法的研究主要有正弦波匹配法[5]、基于距离的波形匹配法[4,6-7]以及相似三角波的匹配法[3,8-9]。
2.1 正弦波匹配延拓
文献[5]提出一种使用正弦函数进行端点延拓的方法。其思想是根据端点至首个极值之间的波形特征,构造出一段幅值、频率、相位与其近似匹配的正弦波实现数据的外延(图2)。

图2 正弦波匹配延拓
该方法将近端点的波形近似看作是某正弦波的一部分,通过该段波形构造出一段近似匹配的波形加以延拓,实现了波形的平顺延拓。但该方法仅仅依靠近端点处的数据特征实施延拓,割裂了近端点处信号与内部信号的联系,无法真实的反映信号的变化趋势及内部特征。
2.2 基于距离的波形匹配法
邵晨曦等[4]将基于距离函数的波形匹配法应用于EMD端点延拓,取得了较好的效果。随后,王婷等[6-7],也分别运用相似的算法实现了EMD端点延拓。这类的延拓的思想是,在波形内部寻找一段与近端点处子波(S1)相似的匹配波形,截取匹配波形(Sj)前一段子波(S’)对端点进行延拓。如图3所示,两子波的匹配距离为:
(2)
式中,s1(i)、sj(i)分别为两子波第i个点的值,N为子波数据长度。取d(S1,Sopt)=min(d(S1,Sj)),截取Sopt前包含两个极值(或更长)的子波S’作为匹配波形平移至端点处实现延拓。

图3 基于距离的波形匹配过程
该方法用原始波形内部的一段子波实现延拓,不但充分考虑了信号近端点处的数据变化趋势信息,同时兼顾了端点处信号与内部信号的联系,在获得波形平顺延拓的同时,维持了信号的原始特征。但是,由于该方法建立在子波数据逐点比对的基础上,因此要求子波间的数据长度严格一致,导致在应用中存在一些问题。
(1)致使无意义的子波截取
当波形的时间尺度变化较大或子波较长时,难以保证所截取的子波在参考极值两侧具有相同的增减特性。如图4,按照等长度截取子波S1及S8,其中S8包含了两个极大值点,使得匹配失去实际意义。
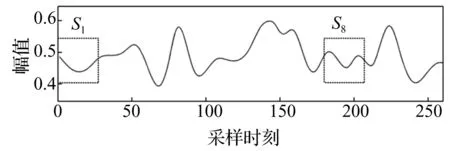
图4 等长度子波截取时的错误
(2)端点位于极值附近时预测准确性差
按照距离匹配算法,当端点数据位于极值附近时,由于可用数据相对较少,将难以准确预测数据的走势。以常用仿真信号为例,表达式为:

t∈[0,500]
(3)
由图5所示,端点距极大值只有一个点距。整体上看,与S1对应匹配的是S9和S17,但是计算结果(表1,精确到10-5)显示S13与S1匹配距离最小。由小窗口可看出,匹配错误是由于匹配数据太少,子波S13在形状上和S1更加接近。

表1 各子波与S1的匹配距离分布

图5 端点位于极值附近时的错误匹配
三角波匹配法,是指以端点与邻近两个极值点所构成的三角形波形为匹配子波,构造三角波形的匹配算法以实现波形的延拓。其突出的特点是不要求子波长度相等(图6)。文献[3,8]分别研究了三角波相似匹配的问题,但并未提及三角波起始点的确定方法。文献[9]将自适应三角波匹配应用于局部均值分解的端点延拓,采用等比关系确定三角子波起始点t(i)的方法:
(4)
或:
(5)
其中:t(mi)是第i个极大值的时刻位置,t(ni)是第i个极小值的时刻位置。
由式(4)可知,t(i)的确定建立在A、B两个三角形相似的基础上。而在实际应用中,难以保证t(ni-1)于t(ni)之间一定存在一点,使得A、B两三角形相似。即,根据式5计算所得t(i)不一定位于t(ni-1)和t(ni)之间,同样使得截取的三角子波无意义(如图4),更无法保证所截取的三角子波具有最佳的匹配度。

图6 三角波匹配法
3 自适应三角波匹配延拓算法
综上所述,正弦波延拓割裂了与内部波形的联系;距离函数匹配法要求子波长度相等,易因数据较少而无法真实反映波形宏观走势,而增加子波长度时易导致无意义的匹配计算;三角波匹配法,不要求子波长度相等,但固定比例法截取子波,难以保证其有效性和匹配的准确性。本文在此基础上提出一种自适应的三角波匹配算法。以首个极值为极大值情况下的左端点延拓为例说明算法步骤。
(1)提取极值点
设,信号x(t)分别有M个极大值和N个极小值;x(i)为信号第i点的数值,m(i),x(m(i)),分别为第i个极大值的序列位置和数值;n(i),x(n(i))分别为第i个极小值的序列位置和数值。
(2)截取模板子波
如图7,截取从端点至第二个极值点间的数据构成模板子波,设为S1。
(3)局部寻优
如图7,须在n(i-1)至m(i)寻找一个时刻点t(i)=j作为三角波的起点。对于每一个固定的i∈[2,n],取j∈[n(i-1)m(i)],则以x(j)、x(m(i))、x(n(i))为顶点共可构成m(i)-n(i-1)个三角波,设为Si(j)。求取一点t(i)=j,使得Si(j)与S1的匹配度最大。
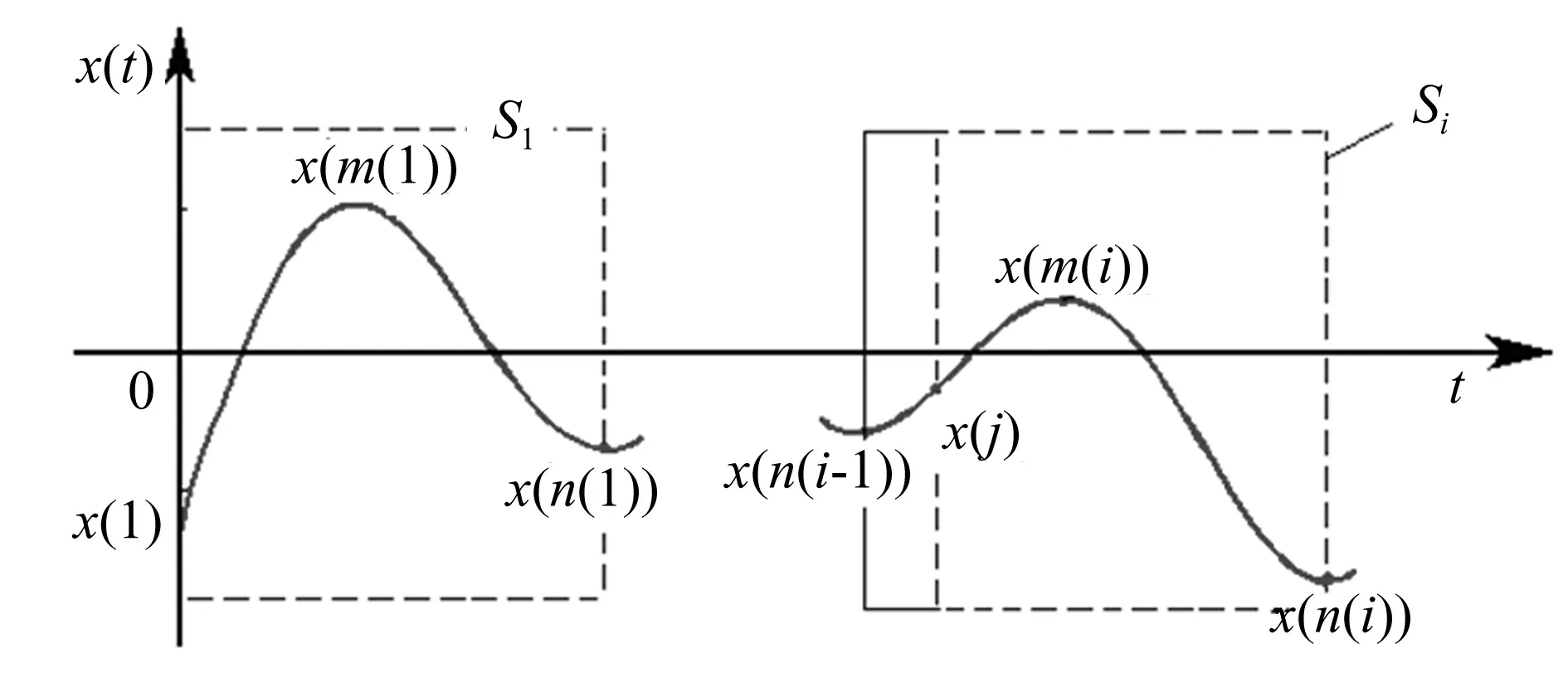
图7 自适应三角波匹配算法
为了在全面反映子波整体形状特征的同时突出延拓的平顺性,文章将单边波斜率及端点幅值差引入到波形匹配计算中。
令:Xi(j)为第i个极大值时,以j时刻为起点,左边波的斜率匹配度:
i∈[2,M],j∈[n(i-1),m(i)],下同。
令:Yi(j)为左边波的幅值匹配度:
令:Oi(j)为右边波幅值匹配度:
令:Pi(j)为右边波时刻匹配度:
令:Qi(j)为端点幅值差匹配度:
其中:a=[x(1)-x(n(1))]×[x(t(i))-x(n(i))]
则,令三角波Si(j)与S1的匹配度Mi(j)为:
Mi(j)=w(Xi(j),Yi(j),Oi(j),Pi(j),Qi(j))
(6)
其中w为各匹配度的权重向量,默认为等权重。
取t(i)=j=find[Mi(j)=maxMi(j)],t(i)即为第i段三角子波的起始点。
(4)全局寻优
记第i个极大值对应的由t(i)截取的最佳三角子波记为Mi。取r=find(Mi=maxMi),则r为最佳匹配子波对应的极值点位置。按照2.2节所述方法可实现左右两端点的匹配延拓。
(5)细节处理
在实际应用中,由于波形长度限制,或难以找到匹配度较高的子波,设置匹配阈值λ∈(0,1),当M(i)<λ时,可采用相似极值延拓[10]或镜像延拓法[11]处理,文中采用镜像延拓法。一般地,信号越长、规律越强,λ取值应越大。
4 算例验证分析
为验证自适应三角波形匹配延拓的有效性,分别采用正弦波延拓法、基于距离函数的波形匹配延拓法以及支持向量回归机(Support Vector Regression,SVR)预测延拓法[12]对仿真信号与实测信号进行对比验证。
4.1 仿真信号分析
采用本方法对式3中信号进行匹配计算,由表2可看出(精确到10-5),该方法实现了准确的波形匹配。由图8~9可看出,正弦波匹配法虽然一定程度上抑制了端点效应,但是没能正确反映信号变化趋势,分解过程出现较大波动;采用距离函数法匹配时,出现了错误匹配现象,致使各分量在端点处出现了变形;自适应三角波匹配延拓与支持向量机预测延拓法,均实现了较为准确延拓。其中w取默认等权重,λ取0.9;SVR延拓点数为100个,支持向量个数为200。
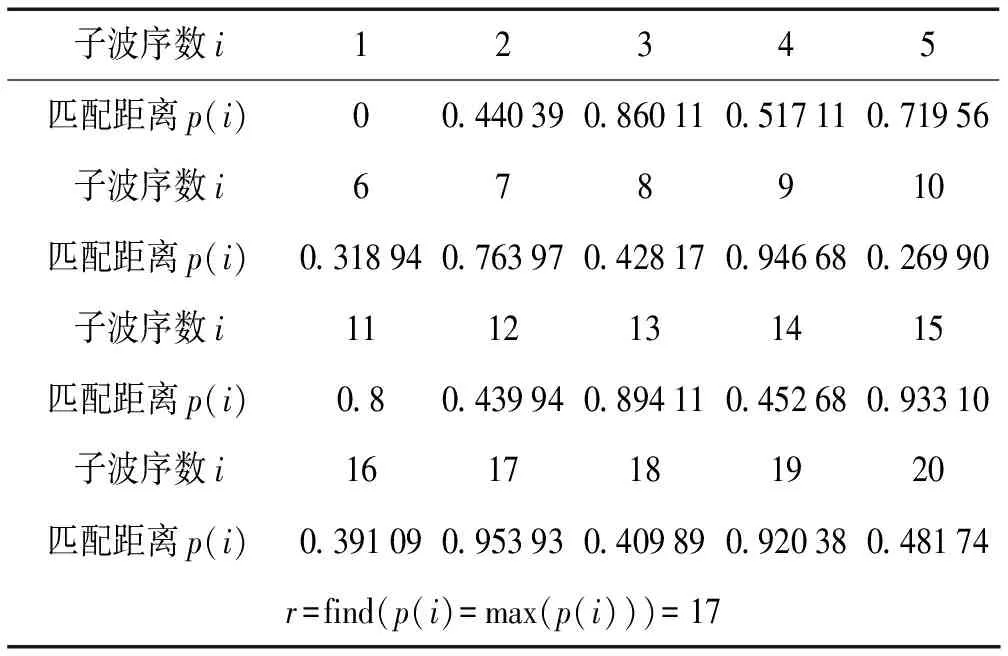
表2 各子波与S1的匹配度

图8 各种延拓方法延拓结果对比
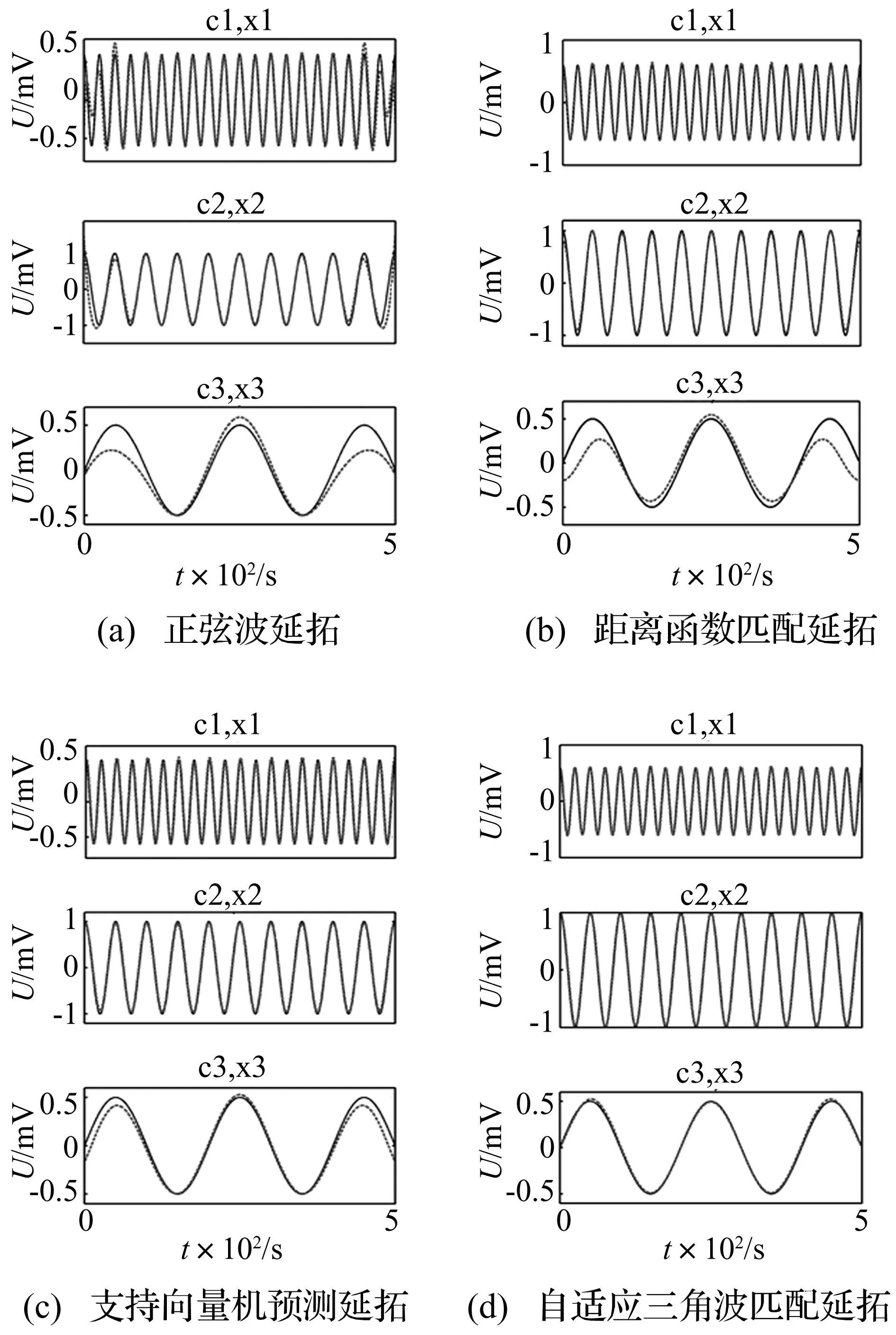
图9 采用各种延拓方法处理的EMD结果
表3显示(精确到10-6),采用自适应三角波匹配延拓法,使EMD处理精度得到显著提高,对于这种规律信号,这些误差基本上是由于包络拟合误差所产生。
4.2 实验信号分析
图10为某轴承振动信号截取的片段,从小窗口可看出,a,b两段波形具有较高的相似性,若能实现准确的匹配延拓,将有效抑制EMD的端点效应问题,提高分解精度。
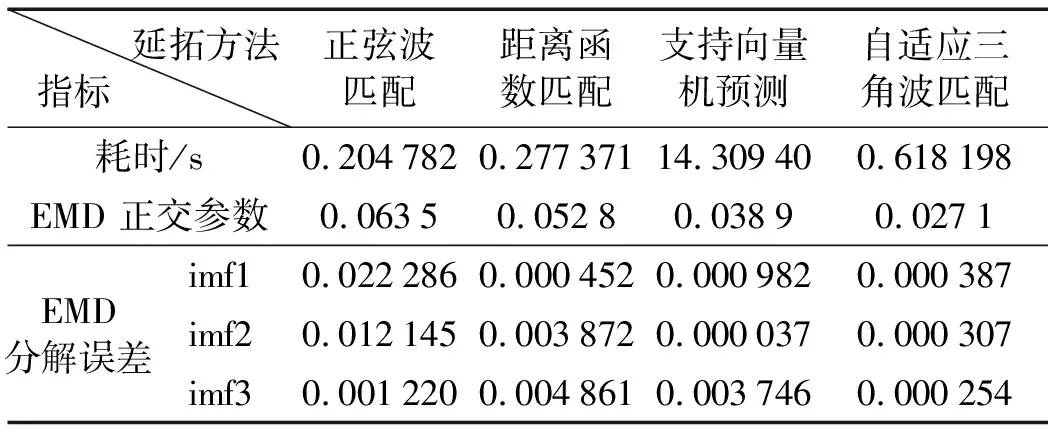
表3 仿真信号EMD分解指标

图10 某轴承振动信号片段
由图11~12可知,采用距离函数匹配延拓法,在EMD处理过程中,在左端点处出现了较明显的波动;自适应三角波匹配延拓法,较好的抑制了EMD端点效应。表4显示,自适应三角波匹配延拓法,分解精度较高,且不需要大量样本学习计算,运行速度比SVR方法有大幅提升。其中w取默认等权重,λ取0.8;SVR延拓点数为50个,支持向量个数为100。

图11 各方法延拓结果对比

表4 实测信号的EMD分解指标

图12 两种延拓方法EMD结果的前5项
5 结 论
本文在总结现有波形匹配延拓方法特点与不足的基础上,提出了一种自适应的三角波形匹配延拓方法。该方法有以下有点:
(1)采用三角波匹配法实现延拓,规避了子波等长度匹配所导致的问题;
(2)通过改进三角波匹配算法,自适应地截取最佳匹配三角子波,改善了固定比例截取子波时产生的问题,保证了子波截取的有效性与合理性。
(3)通过局部寻优与全局寻优相结合的方法实现匹配子波的截取与定位,提高了波形匹配延拓的准确性。
(4)匹配度算法中加入了单边斜率匹配度和端点幅值差匹配度,突出了延拓的平顺性,强化了近端点波形与内部波形间的联系。
仿真及实验数据分析表明,该方法提高了波形匹配的准确性,可有效遏制EMD端点效应问题,显著提高分解精度。文中仅对匹配度阈值λ的取值方法做了定性分析,尚需进一步研究其取值及调整方法,另外权重向量w的取值及调整方法同样需要进一步深入研究。
参 考 文 献
[1]Huang N E,Shen Z,Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].Proceedings of the Royal Society of London Series.1998,454:903-995.
[2]贺 智,王 强,沈 毅,等.希尔伯特—黄变换端点效应抑制算法综述[J].软件,2011,32(10):1-7.
HE Zhi,WANG Qiang,SHEN Yi,et al.Survey on end effects Mitigation of Hilbert-Huang Transform [J].Software,2011,32(10):1-7.
[3]盖 强,马孝江,张海勇,等.一种消除局域波法中边界效应的新方法[J].大连理工大学学报,2002,42(1):115-117.
GAI Qiang, MA Xiao-jiang, ZHANG Hai-yong, et al.A new method to eliminate the boundary effect in local wave method [J].Journal of Aalian University of Technology, 2002,42(1):115-117.
[4]邵晨曦,王 剑,范金锋,等.一种自适应的EMD端点延拓方法[J].电子学报,2007,35(10):1944-1947.
SHAO Chen-xi,WANG Jian,FAN Jin-feng,et al.A self-adaptive method dealing with the end issue of EMD [J].Acta Electronica Sinca,2007,35(10):1944-1947.
[5]黄先祥,李胜朝,谢 建.新型经验模式分解端点效应消除方法 [J].机械工程学报,2008,44(9):1-5.
HUANG Xian-xiang,LI Sheng-chao,XIE Jian.New approach to dealing with the end effect of empirical model decomposition [J].Chinese Journal of Mechanical Engineering,2008,44(9):1-5.
[6]王 婷,杨莘元,李冰冰.一种改善EMD端点效应的新方法[J].哈尔滨理工大学学报,2009,14(5):24-26.
WANG Ting,YANG Xin-yuan,LI Bing-bing.A new method for end effect of EMD [J].Journal of Harbn University of Science and Technology,2009,14(5):24-26.
[7]杨 庆,陈桂明,薛冬林.基于最小平方距离相关的 EMD改进算法及应用[J].振动与冲击,2011,30(6):62-66.
YANG Qing,CHEN Gui-ming,XUE Dong-lin.Improved method for empirical mode decomposition based on SSDA and its application[J].Journal of Vibration and Shock,2011,30(6):62-66.
[8]钟佑明,赵 强,周建庭.一种基于本征波匹配的EMD边界处理方法[J].振动与冲击,2012,31(1):16-19.
ZHONG You-ming,ZHAO Qiang,ZHOU Jian-ting.A method for EMD boundary processing based on intrinsic wave matching [J].Journal of Vibration and Shock,2012,31(1):16-19.
[9]张 亢,程军圣,杨 宇.基于自适应波形匹配延拓的局部均值分解端点效应处理方法[J].中国机械工程,2010,21(4):457-462.
ZHANG Kang,CHENG Jun-sheng,YANG Yu.Processing method for end effects of local mean decomposition based on self-adaptive waveform matching extending [J].China Mechanical Engineering,2010,21(4):457-462.
[10]沈 路,周晓军,张志刚,等.Hilbert-Huang变换中的一种端点延拓方法[J].振动与冲击,2009,28(8):168-171.
SHEN Lu,ZHOU Xiao-jun,ZHANG Zhi-gang.A endpoint extension method for Hilbert-Huang Transform [J].Journal of Vibration and Shock,2009,28(8):168-171.
[11]Rilling G,Flandrin P, Gonçalvès P.On empirical mode decomposition and its algorithms[J].IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03,2003,3:8-11.
[12]Cheng J S,Yu D J,Yang Y.Application of support vector regression machines to the processing of end effects of Hilbert-Huang [J].Mechanical Systems and Signal Processing,2007,21:1197-1211.

