桥墩不均匀沉降对高速列车运行安全影响研究

王昆鹏， 夏 禾， 郭薇薇， 曹艳梅， 吴 萱， 孙 璐

(1.北京交通大学 土木建筑工程学院,北京 100044； 2.东南大学 交通学院,南京 210096)

我国铁路中诸多线路架设在深厚软土地质条件的东南部沿海地区。研究表明，在循环荷载长期作用下软土地基会产生较大附加沉降，如某城际高速铁路投入运营后，部分桥梁产生较大附加沉降。黄茂松等[1]基于不排水循环三轴试验及临界状态理论，研究不同初始静偏应力及动应力的应力历史综合影响下饱和软黏土不排水循环累计变形特性。宫全美等[2]通过室内动三轴试验提出基于基床土长期变形等效的列车正弦荷载等效方法，即用一个半正弦波代表一个转向架的列车动荷载。对公路交通荷载所致软土地基累积沉降问题，Chai等[3]通过假设土体所受剪应力小于临界剪应力、土为正常或轻微超固结，给出能考虑土体初始状态的计算公式；魏星等[4]提出能考虑排水条件影响的饱和软土累积变形计算经验公式。随地铁运营的发展，地铁荷载引起的软土地基沉降引起关注。刘明等[5]采用拟静力有限元计算与经验拟合计算模型相结合方法预测地铁荷载作用下饱和软黏土长期沉降量；赵春彦等[6]采用Mesri蠕变模型、考虑土应力历史循环累积变形及累积孔压模型分别模拟土体三类变形，结合有限元计算及三轴试验，提出叠交隧道长期沉降预测方法。而对列车荷载引起的桩基础沉降研究较少。

高速铁路对线路条件要求较高。为保证行车安全，国家规范对运营线上桥梁墩台产生的均匀沉降及相邻墩台不均匀沉降有严格限制。宋国华等[7]通过假设桥墩发生一定量不均匀沉降，利用车-线-桥垂向系统模型研究桥墩不均匀沉降时列车运营安全性问题。列车通过桥梁时产生的荷载会通过桩基础传到软土地基中，线路运营过程即相当于对软土循环加载过程，亦会使软土地基产生附加沉降，影响列车运行安全性。因此，对软土处桥墩在列车荷载循环作用下的沉降规律及桥墩不均匀沉降对行车安全影响系统研究意义重大。

1 模型分析

目前对列车引起的桩基沉降研究较少。本文对此采用车辆-桥梁动力相互作用模型、桩基础-地基沉降模型进行研究，车辆-桥梁-桥墩-桩基础-地基系统见图1。利用车辆-桥梁动力相互作用模型获得列车过桥时桥墩支反力时程，并作为外部激励施加到桩基础-地基沉降模型中，求出软土累积塑性变形，研究运营列车对桩基础累积沉降的影响规律；将由桥墩沉降产生的附加线形变化叠加到原始轨道不平顺中，考虑由附加变形引起的竖向类离心力影响，利用车辆-桥梁动力相互作用模型研究桥墩不均匀沉降对列车行车安全影响。

图1 车辆-桥梁-桥墩-桩基础-地基系统模型

1.1 车辆-桥梁动力相互作用模型

1.1.1 车辆子系统模型

车辆模型采用2D平面模型，见图2。车辆-桥梁子系统模型中设轮对与轨道密贴，轮对不具有独立自由度，而每节车辆有6个独立自由度，车辆运动方程为[8]：

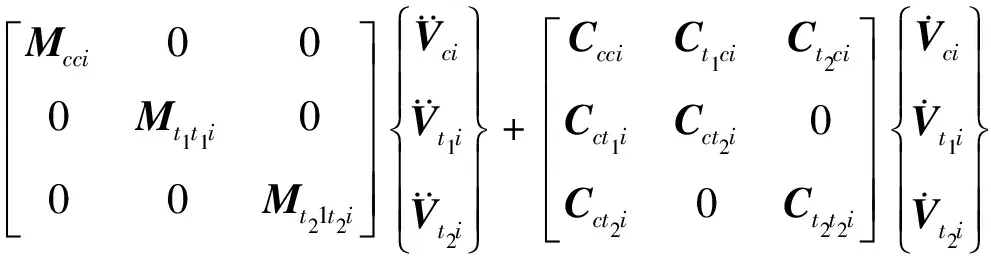
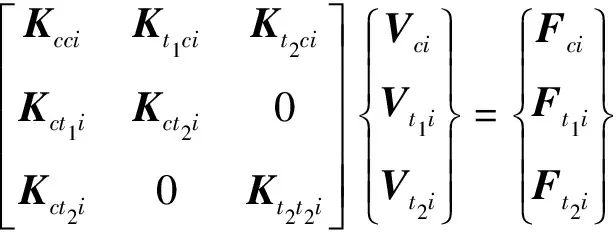
(1)

运动方程中阻尼子矩阵与刚度子矩阵形式相同，只需将刚度子矩阵中k用c代替即可。运动方程中荷载向量由两部分组成，即：

(2)

其中：第一部分为作用在车体及两转向架的外荷载，如风荷载等；第二部分为通过一系弹簧、阻尼器传到前、后转向架的力。

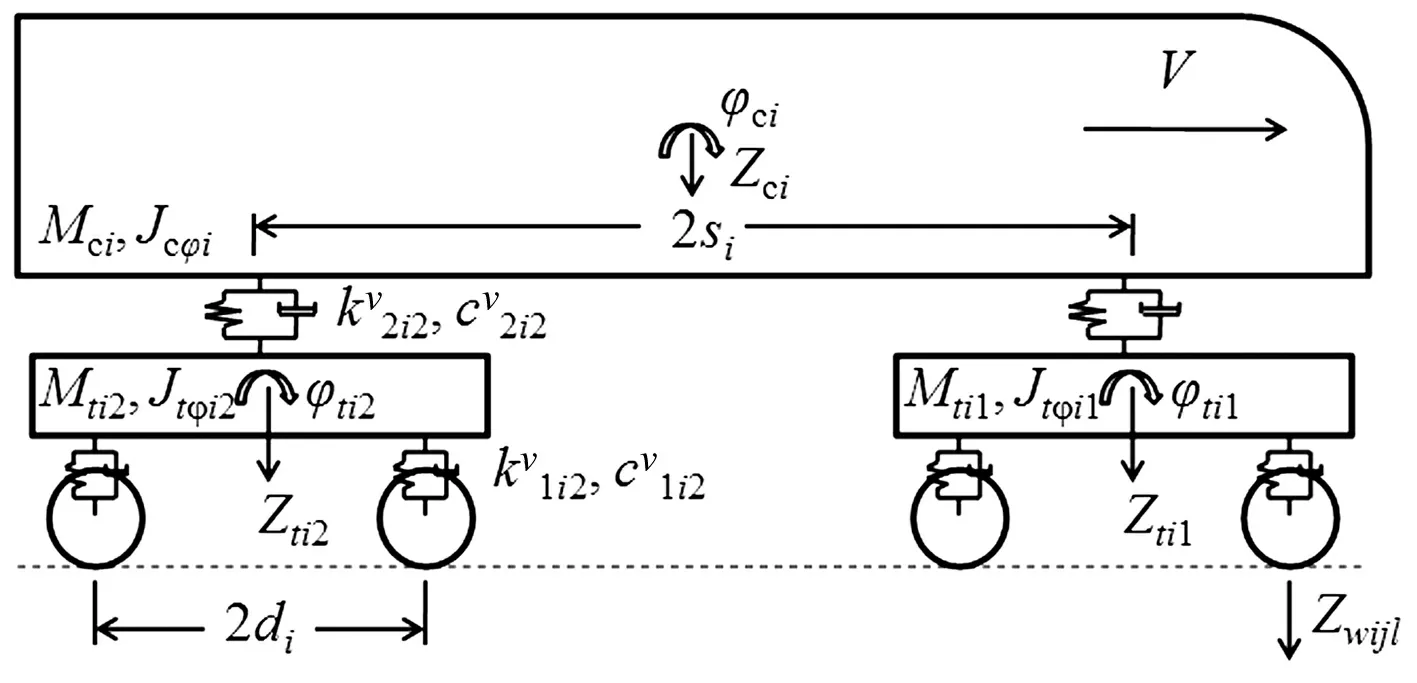
图2 车辆动力模型

1.1.2 桥梁-桥墩子系统模型

本文主要研究桥墩不均匀沉降所致附加轨道变形影响。为集中分析该影响，不考虑轨道弹性变形，设轨道与桥梁间无相对位移，墩底按固结处理，建立2D有限元模型，其结构运动方程为：

(3)

式中：MB，CB，KB分别为桥梁结构质量、阻尼、刚度矩阵；XB为桥梁结构位移矢量；FB为作用于桥梁结构的外荷载矢量。

(4)

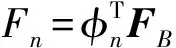
通过第i辆车第j个转向架的第l个轮对作用于桥面的竖向力可据该轮对运动加速度及其与转向架相对位移、速度确定：

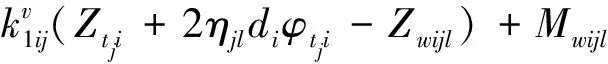
(5)

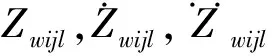
1.2 桩基础-地基沉降模型

对桩基础-地基沉降模型简化：由于在局部均布荷载作用下，半无限土体中产生的应力在横向衰减较快，故忽略相邻桩基础影响；而桩基础材料弹性模量远大于软土弹性模量及群桩对桩间土影响，故将群桩及桩间土视为整体，即将群桩基础等效成半径为r[9]的单桩基础，将桩基础-地基模型简化为轴对称模型。等效原则为等效单桩与群桩外包络矩形、群桩与群桩(含桩间土)分别具有相同面积、竖向刚度及质量；求解外荷载作用下土体中各点应力状态时，土体材料采用弹性模型[5]；认为桩基础沉降量等于桩基础底面处土体的沉降量；设地基位于基岩之上，即认为模型底部的竖向位移为零。计算简图见图3，其中L为地面距桩基底面距离；l为桩长。

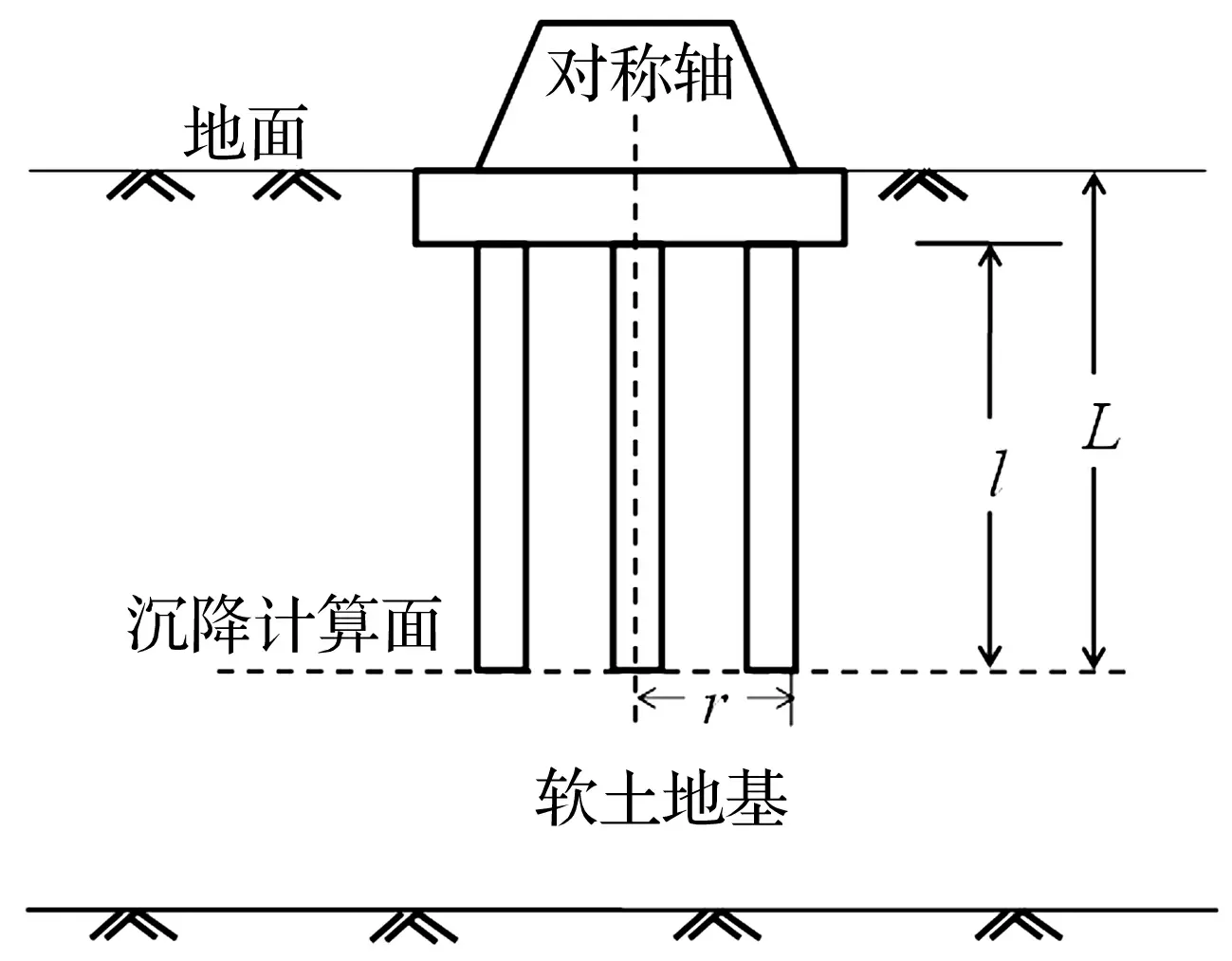
图3 桩基础-地基计算简图

1.2.1 软土累积沉降计算模型

通常在研究循环荷载下软土的累计塑性变形时，采用基于经验拟合公式的实用简化计算模型[1,10-12]。此模型分为基于第一次循环变形的计算模型与基于循环破坏概念的计算模型两类。本文采用文献[1]的经验拟合计算模型，即将第一次循环变形与循环破坏概念结合考虑，引入相对偏应力水平概念D*，综合考虑初始静偏应力及动偏应力对软粘土循环加载特性影响，表达式为：

D=q/qult

(6)

(7)

式中：D为偏应力水平；q=σ1-σs为偏应力；qult为不排水破坏强度；Ds=qs/qult为静偏应力水平；Dp=(qd+qs)/qult为峰值偏应力水平；Dmax为可能达到的最大偏应力水平，取Dmax=1。

本文采用基于修正剑桥模型理论推导所得表达式计算土体不排水破坏强度qult[5]：

(8)

其中：pc为土体平均有效固结压力，可由此处土体由土层自重产生的竖向应力乘以土体侧限系数K0确定；λ，κ分别为e-lnp空间中正常固结线及回弹线斜率；M为修正剑桥模型临界状态线斜率。

模型中将软土累积沉降S分为循环荷载作用下土体中不排水累积变形引起的沉降Sd与由循环荷载引起的累积孔压消散所致固结沉降Sv两部分。

1.2.2 不排水累积变形计算模型

第一次循环塑性应变ε1与相对偏应力水平D*之关系为：

ε1=aD*m

(9)

式中：a，m为试验参数。

荷载循环作用N次后的累积变形εp与第一次循环塑性应变ε1的简化计算关系为[10]：

εp=ε1Nb=aD*mNb

(10)

式中：b为试验参数。

1.2.3 累积孔压计算模型

累积孔压u与相对偏应力水平D*及循环次数N的关系与不排水累积变形类似，为[10]：

u/pc=ξD*nNβ

(11)

式中：ξ，n，β为试验参数；其余参数同前。

1.2.4 参数确定

以上式中所需土体参数可通过对土样室内循环三轴试验结果拟合获得。本文计算模型参数见文献[11]，为基于上海软土进行的一系列试验拟合所得，见表1。

表1 模型参数取值

土体不同试验参数不一，此处仅作为参考取值进行计算，研究列车荷载对桩基础累积沉降影响规律。

1.2.5 桩基础长期沉降计算

采用分层总和法计算桩基础在循环荷载作用下的长期沉降量S，计算式为：

(12)

式中：εp为第i层土累积塑性应变；ui为第i层土不排水循环累积孔压；mvi为第i层土体积压缩系数；U为第i层土固结度。模型中设累计孔压能及时消散，故取U= 1；hi为第i层土厚度；n为压缩总层数。

1.2.6 沉降限值

《高速铁路设计规范(试行)》(TB10621-2009)中对不同桥梁结构墩台总沉降量与墩台施工完成时的沉降量之差进行限定，对静定结构具体要求见表2。

表2 墩台沉降量限值

超静定结构相邻桥墩均匀沉降量之差容许值，应据桥墩不均匀沉降对结构产生的附加应力影响确定。

2 数值计算分析

2.1 模型参数

采用京沪线3×32 m标准梁，箱形截面；桥墩为双柱墩，墩高6 m，单柱截面尺寸3×2.2 m，柱间净距为2.4 m，见图4；简支梁竖向基频4.65 Hz；桥梁阻尼比取

0.05。采用德国ICE3列车，八辆列车编组，编组形式为动车 + 6拖车 + 动车，动车及拖车轴重分别为156.7 kN，143.1 kN。

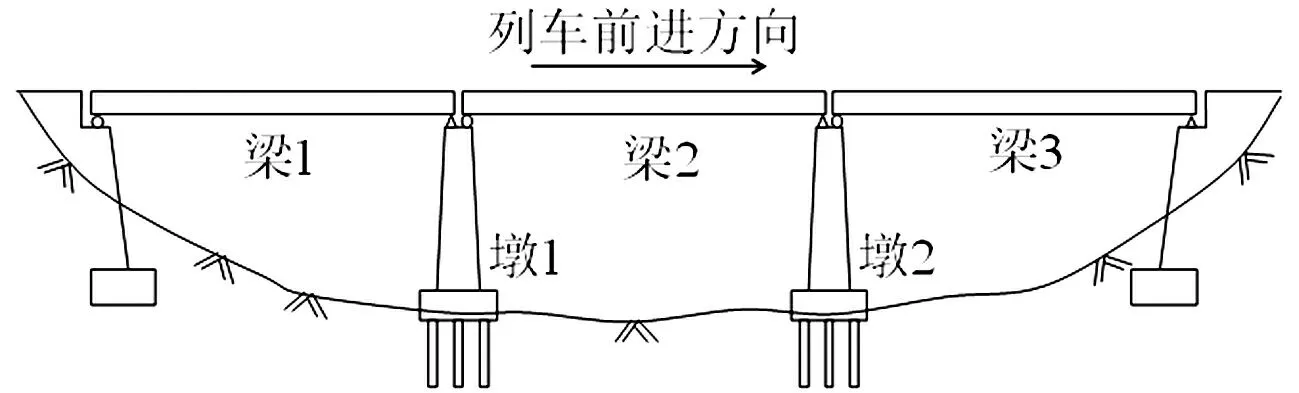
图4 桥梁结构示意图

计算所用轨道不平顺基于德国低干扰谱利用三角级数法生成，并考虑轨道不平顺速度及加速度影响[13]，见图5。图5(b)、(c)分别为列车速度V= 180 km/h时轨道不平顺速度、加速度。桩基础模型参数：采用京沪线一座实际桥梁尺寸数据，承台尺寸6×9×2.5 m，每个承台有8根桩；桩径1.0 m，桩长分别为35 m，40 m，45 m。

桩基础-地基模型中土体参数见文献[4]，地基土体共4层，自上而下分别为填土、灰色粉质黏土、灰色淤泥质黏土及暗绿色粉质黏土，各土层参数见表3。

图5 轨道不平顺波形

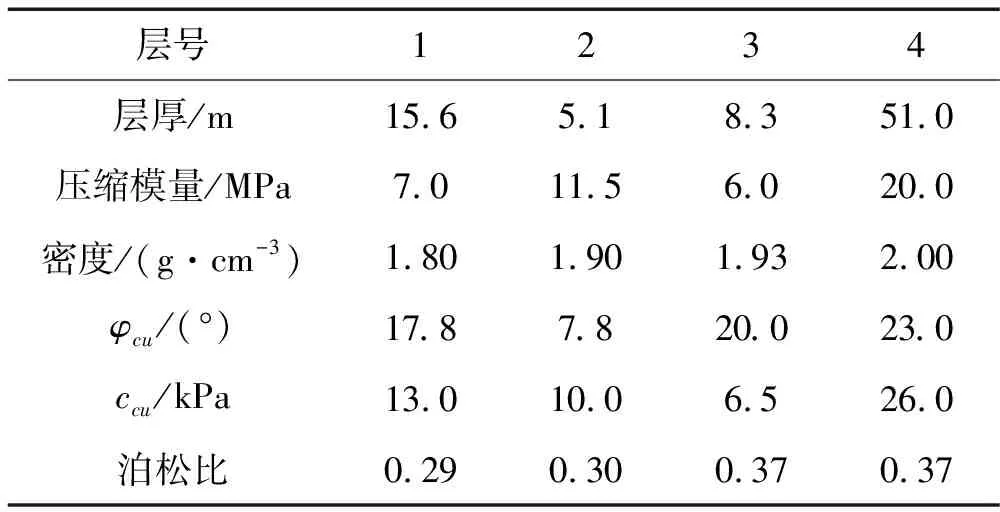
表3 土层基本参数

2.2 沉降计算及分析

将列车荷载与动三轴试验中正弦荷载建立联系至关重要，文献[2]采用一个半正弦波等效一个转向架的列车动荷载。本文据桥墩所受列车荷载时程曲线特点及处理方法[5]，将列车过桥时桥墩支反力等效为一个半简谐荷载，即列车过桥次数N即循环荷载加载次数N。据有关文献研究成果，软土附加塑性变形主要集中在桩底一定深度范围内，随深度的增加，附加塑性变形量急剧降低，本文将压缩层厚取30 m。

图6、图7为不同速度下，列车过桥次数不同时桥墩沉降量(l= 45 m)。由图6看出，软土的累积沉降量S与循环次数N存在指数关系，当循环荷载作用次数N较低时，软土附加沉降速度较快；随循环荷载作用次数N的增大软土沉降速度逐渐降低。设列车发车间隔为5 min，则运营一年加载次数N为10万次，该线路在260 km/h速度下运营1、2、5、10年后的累积沉降量分别为6.8 mm、9.0 mm、13.1 mm、17.4 mm。由图7看出，循环次数N相同时，随列车速度的增大，累积沉降量S呈增加趋势，但列车速度等于140 km/h及200 km/h时，沉降出现峰值，此因为该两速度较接近桥梁第一类竖向共振速度[8]，导致桥梁动力响应增大，从而使软土累积沉降S增加。桥梁第一类竖向共振速度表达式为：

(13)

式中:Vbr为引起桥梁共振的列车速度(km/h)；fbn为桥梁第n阶竖向自振频率，其中fb1= 4.65 Hz；dv=24.775 m为荷载列车间距。依此公式求出该桥梁第一类竖向共振速度为138.2 km/h及207.4 km/h。

图8为列车速度V=180 km/h时，软土累积沉降量S与桩长l之关系。由图8看出，累积沉降量S对桩长l的变化较敏感，随l的增大，S迅速减小。因此增加l能较好减小桩基附加沉降量。

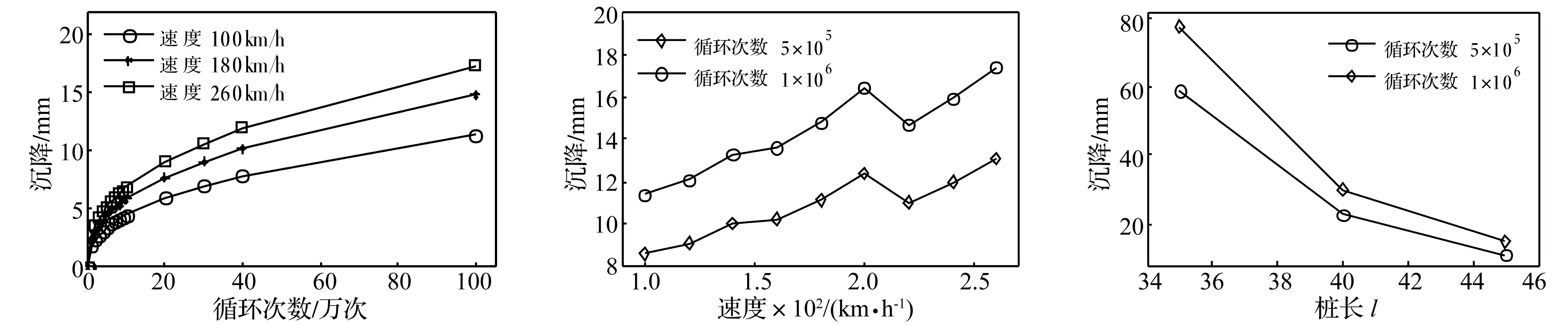
图6 桩基沉降量与循环次数之关系 (l = 45 m)

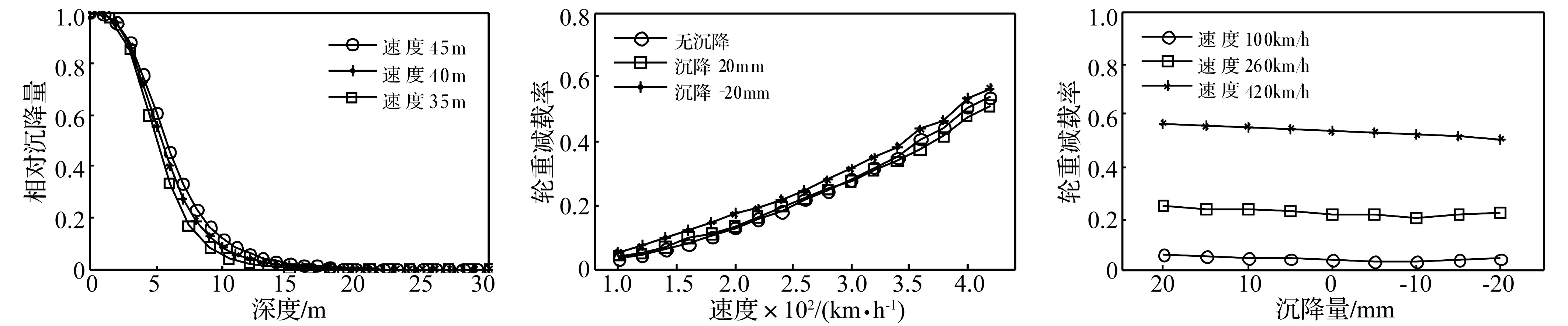
图9 相对沉降量与深度之关系 (V=180 km/h)

图9为列车速度V= 180 km/h、循环加载次数N=1×106、不同桩长l时桩底不同深度处土层相对沉降量沿深度的变化曲线(相对沉降 = 某土层处沉降 / 桩基础底面处土层沉降，深度以桩基底面处标高为0 m)。由图9看出，桩长不同，软土地基沉降分布模式类似，软土累积塑性变形主要发生在桩底约10 m深度范围内，10 m以下软土层变形量较小，因此对桩基础底部一定深度软土层进行地基处理可有效降低桩基础的累积沉降量。

2.3 不均匀沉降对行车安全影响

据沉降计算知，运营10年后软土地基的累积沉降量S约为17.4 mm。本文设桥墩1发生-20 mm，-15 mm，-10 mm，-5 mm，5 mm，10 mm，15 mm，20 mm 8种不均匀沉降工况(负值表示桥墩1无沉降，相邻桥墩有沉降)，计算速度范围100～420 km/h，步长20 km/h。由于轨道的连续性，当桥墩发生沉降时轨面会变为类似圆弧的曲面，列车行驶至此处时会受到竖向类离心力，本文考虑该类离心力影响。

图10、图11为不同速度V及沉降工况下，列车过桥时最大轮重减载率。由二图看出，最大轮重减载率随列车速度的增大迅速增大。据式(5)，轮轨力对轨道不平顺加速度较敏感，且轨道不平顺加速度与车辆速度V间为二次方增大关系，因此轮重减载率会随列车速度V的提高迅速增大。如图5(c)，列车速度V= 180 km/h时，最大加速度绝对值达8.2 m/s2。相邻桥墩沉降引起的相对上拱会使轮重减载率增大，正沉降反而会使轮重减载率略有减小。以列车速度V= 420 km/h，沉降量为-20 mm，0 mm，20 mm为例，列车最大轮重减载率分别为0.567，0.538，0.509，相邻桥墩沉降引起的相对上拱使轮重减载率逼近容许限度0.60。此为由类离心力的存在所致。相邻桥墩发生沉降时，车辆所受类离心力为背向桥墩方向，从而使轮重减载率增加；桥墩发生正沉降时，类离心力指向桥墩方向，反而会使轮重减载率减小。由此，相邻桥墩沉降引起的相对上拱对行车安全更加不利。

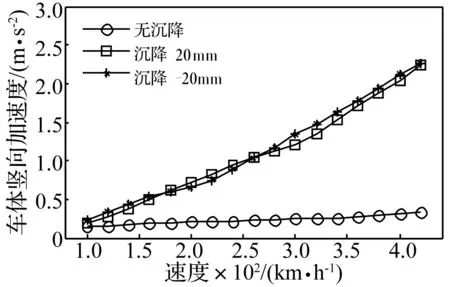
图12 车体竖向加速度与车速之关系

图12、图13为不同速度V及沉降工况下，第5节列车车体中心处最大加速度。由二图看出，列车通过发生桥墩沉降的桥梁时，不论桥墩以何种方式沉降，车体竖向加速度均会急剧增大，且在相同速度下，随沉降量的增加呈类线性增长，此时车体竖向加速度超出规范中舒适性限值1.3 m/s2。相比桥墩不均匀沉降对车辆轮对减载率影响，对车体加速度影响更显著。

图14为不同车速V及沉降工况下，桥跨1的最大跨中加速度及最大跨中挠度。由图14看出，桥梁跨中动力响应并未随V的增大而单调增加，而在某些速度点处出现峰值[8]；桥梁跨中加速度响应对桥墩不均匀沉降不敏感，此因轨道的存在使由沉降产生的附加线形变化光滑，不会使轮轨力产生太大附加冲击。随列车速度的增大，桥墩不均匀沉降对桥梁跨中挠度影响逐渐增大，桥梁跨中挠度与列车速度关系曲线据沉降种类的不同朝不同方向发生偏移，列车通过发生桥墩沉降桥梁时会受到类离心力作用，且方向随沉降种类的不同相反。随列车速度的提高，车辆所受类离心力逐渐增大，致桥墩不均匀沉降对桥梁跨中挠度影响程度逐渐增大。

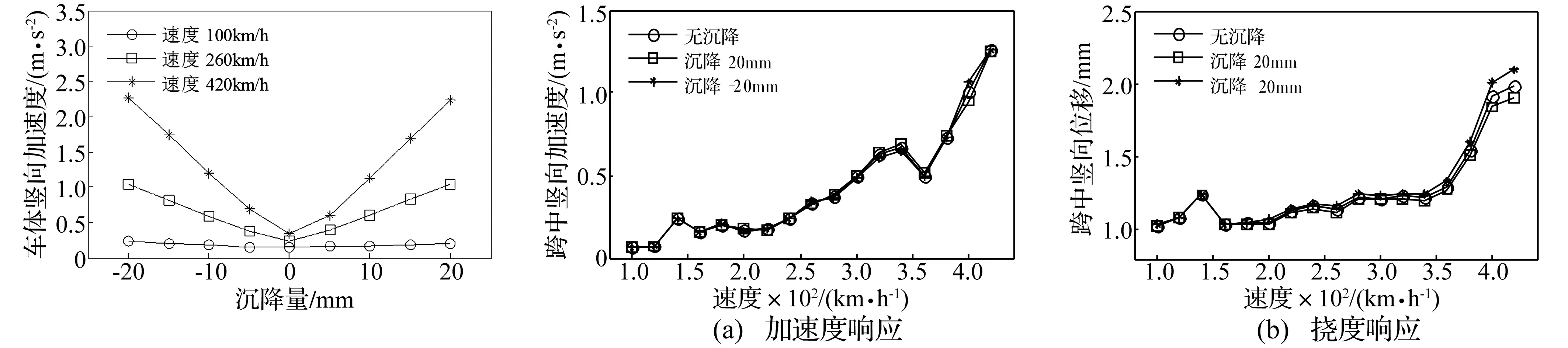
图13 车体竖向加速度与沉降量之关系

3 结 论

(1) 列车循环荷载作用下，桩基础的累积沉降量S受桩长l影响明显，随桩长l的增加，累积沉降量S迅速降低；列车循环加载引起的软土累积沉降主要发生在桩基底部约10 m深的软土层内。

(2) 列车通过发生桥墩不均匀沉降的桥梁时会受竖向离心力作用。对相邻桥墩沉降引起的相对上拱情况，类离心力为背向桥墩方向，使列车轮重减载率增大，此沉降种类对行车安全更不利；桥墩不均匀沉降对车体加速度影响更显著，使车体竖向加速度超出规范中舒适性限值1.3 m/s2。

(3) 轨道的存在使由桥墩不均匀沉降产生的附加线形变化光顺，不会使轮轨力产生太大附加冲击，桥墩不均匀沉降对桥梁跨中加速度响应影响较小；类离心力的存在使桥梁跨中挠度与列车速度V的关系曲线会据沉降种类的不同发生不同偏移。

参 考 文 献

[1]黄茂松,李进军,李兴照. 饱和软粘土的不排水循环累积变形特性[J]. 岩土工程学报, 2006, 28(7): 891-895.

HUANG Mao-song, LI Jin-jun, LI Xing-zhao. Cumulative deformation behaviour of soft clay in cyclic undrained tests[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 891-895.

[2]宫全美, 罗 喆, 袁建议. 提速铁路基床长期累积沉降及等效循环荷载试验研究[J]. 铁道学报, 2009, 31(2): 88-93.

GONG Quan-mei, LUO Zhe, YUAN Jian-yi. Experimental study on long-term cumulative settlement and equivalent cyclic load of speed-up railway subgrade soil[J]. Journal of the China Railway Society, 2009, 31(2): 88-93.

[3]Chai J C, Miura N. Traffc-load-induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(11): 907-916.

[4]魏 星, 王 刚, 余志灵. 交通荷载下软土地基长期沉降的有限元法[J]. 岩土力学, 2010, 31(6): 2011-2015.

WEI Xing, WANG Gang, YU Zhi-ling. FEM of traffic-load-induced settlement of road on soft clay[J]. Rock and Soil Mechanic, 2010, 31(6): 2011-2015.

[5]刘 明, 黄茂松, 李进军. 地铁荷载作用下饱和软粘土的长期沉降分析[J]. 地下空间与工程学报, 2006, 2(5): 813-817.

LIU Ming, HUANG Mao-song, LI Jin-jun. Long-term settlement of saturated soft clay under subway loading[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(5): 813-817.

[6]赵春彦, 周顺华, 袁建议. 地铁荷载作用下叠交隧道长期沉降的半解析法[J]. 铁道学报, 2010, 32(4): 141-145.

ZHAO Chun-yan, ZHOU Shun-hua, YUAN Jian-yi. Semi-analytical solution of overlapped tunnel for long-term settlement under subway loading[J]. Journal of the China Railway Society, 2010, 32(4): 141-145.

[7]宋国华, 高芒芒, 黎国清. 桥梁墩台不均匀沉降时的车桥垂向系统耦合振动分析[J]. 中国铁道科学, 2010,31(2): 29-33.

SONG Guo-hua, GAO Mang-mang, LI Guo-qing. Vehicle-bridge vertical system coupled vibration analysis under the uneven settlement of bridge pile and abutment[J]. China Railway Science, 2010, 31(2): 29-33.

[8]Xia H, De Roeck G, Goicolea J M. Bridge vibration and controls: new research[M].New York:Nova Science Publishers Inc., 2011.

[9]朱 晞, 王大庆. 桩基桥墩考虑土与结构相互作用抗震计算方法的研究[J]. 铁道学报, 1992,14(4): 81-90.

ZHU Xi, WANG Da-qing. A study on the earthquake resistant calculation for pile supported bridge piers in consideration of soil-structure interaction[J]. Journal of the China Railway Society, 1992,14(4): 81-90.

[10]李进军. 交通荷载作用下饱和软粘土长期沉降分析[D]. 上海: 同济大学, 2005.

[11]袁聚云. 软土各向异性性状的试验研究及其在工程中的应用[D].同济大学,2005.

[12]Li D Q, Selig E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering, 1998, 102(12): 1006-1013.

[13]吴定俊, 李 奇, 高丕勤. 轨道不平顺速度项对车桥动力响应的影响分析[J]. 同济大学学报(自然科学版),2006, 34(4):494-498.

WU Ding-jun, LI Qi, GAO Pi-qin. Dynamic response of vehicle-bridge system due to track irregularity coupling with velocity of the vehicle[J]. Journal of Tongji University (Natural Science), 2006, 34(4): 494-498.