离心式压缩机转子系统稳定性控制方法研究

王维民， 齐鹏逸， 李启行， 高金吉

(北京化工大学 诊断与自愈工程研究中心,北京 100029)

离心压缩机作为石油、化工等流程工业的核心设备，其安全高效长周期运行为工程科技界追求目标。近年随运行参数(流量，压力，压比)的提高，转子与静子间微小间隙内流体周向流动产生的作用于转子非保守作用力增大，常导致转子失稳，成为威胁离心压缩机高效长周期运转的主要障碍。采用主动控制方法可提高转子-轴承-密封系统阻尼比即转子稳定性。James等[1]研究通过主动控制方法解决转子稳定性可行性，认为主动控制方法不仅能降低转子过临界时响应幅值、给转子系统增加阻尼、改变轴承载荷等，且亦能在线分析转子系统特性以识别潜在故障并对控制系统进行优化；但存在包括转子本身与控制系统，如控制器带宽、控制策略设计、功耗及力幅值、转子状态可观测性、最优控制算法选择及CPU速度等问题。部分问题能在短时间内解决，有些则需长期努力。NASA 曾会议研究高性能透平机械转子稳定性问题。David等[2-6]对如何通过主动控制，解决转子失稳故障进行深入讨论。

在众多控制方法中，电磁场因可在空间传播，通过非接触方式为转子施加作用力而被认为较理想的控制方式。汪海航等[7]研究认为，由于电磁阻尼器的多频动力特性，通过合理选择静态电流、控制增益及相移量三参数，可有效控制转子多频振动。Skladanek等[8]研究认为，电磁执行机构在转子振动控制方面较压电式执行机构更节能。Shafei等[9]研究用电磁控制器控制圆柱轴承支撑的转子稳定性，并分别研究三种控制方法，认为通过速度反馈方式可更有效控制转子稳定性。Mahfoud等[10-11]用实验方法研究电磁控制器多转子系统稳定性控制的可行性，结果表明，电磁控制器减振效果明显。祝长生等[12]研究带主动电磁阻尼器的裂纹转子系统动力学，认为在主动电磁阻尼器控制系统设计时应考虑转子裂纹影响。

以上研究仅从控制振动效果角度考虑控制系统设计。工程应用需综合考虑能耗因素。不仅涉及消耗功率，且需考虑功率放大器散热等实际问题。本文针对实际压缩机转子，研究位移反馈、速度反馈在振动控制效果及消耗功率的差别，可为电磁控制器的工程应用提供基础。

1 转子稳定性动力学分析

1.1 稳定性控制理论基础

在离心压缩机中，转子、静子间微小间隙内流体周向流动产生的作用于转子非保守作用力为导致转子失稳的主要因素。该力主要产生于叶轮、密封、轴承等处，在动力学中常用交叉刚度描述该作用力大小。其对转子作用力Fc可表述为：

(1)

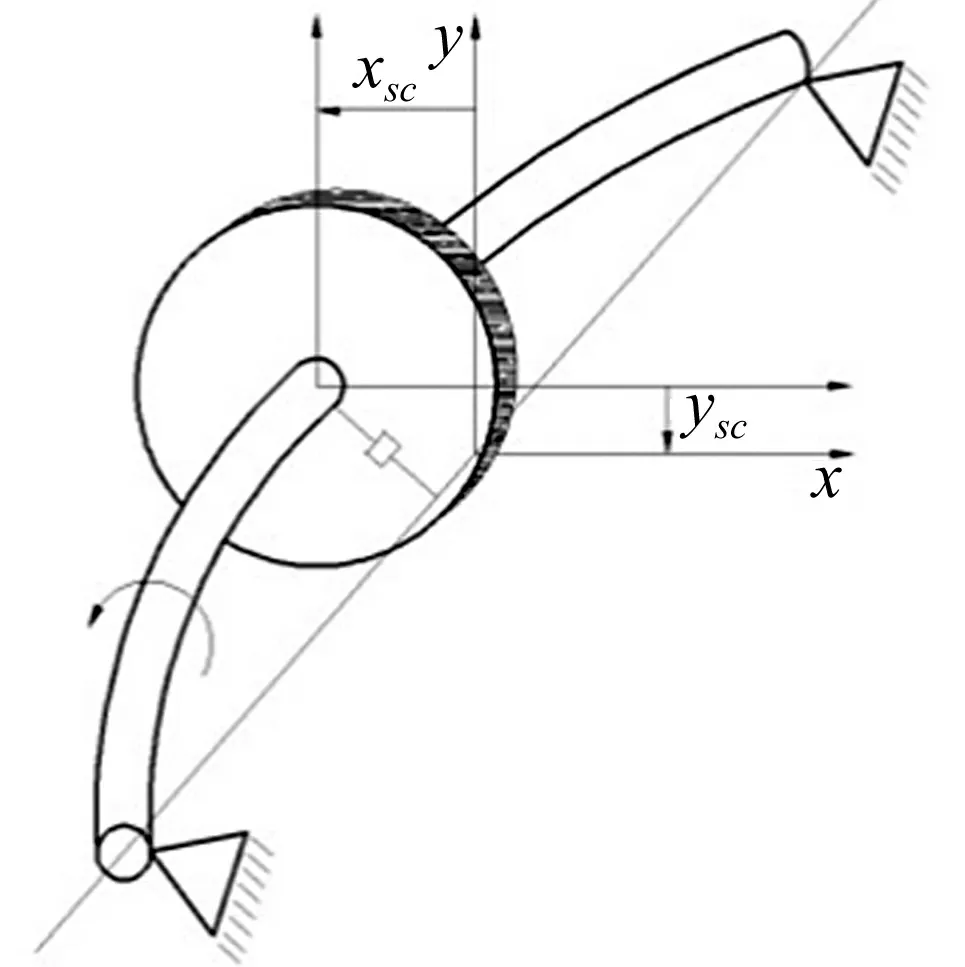
图1 Jeffcott 转子示意图

式中：xs，ys为转子位移；Fcx，Fcy为沿坐标轴x，y向作用力；q为交叉刚度系数。负号表示力方向与转子位移方向相反。

对图1的Jeffcott 转子，据牛顿第二定律，忽略陀螺效应，其运动方程可写为：

(2)

式中：Fsd为阻尼力；cs为阻尼系数；Fsk为弹性恢复力；ks为弹性系数；Fkcross为交叉刚度力；q为交叉刚度系数；Fexcite为作用于转子上其它激振力。

将上式重新整理为：

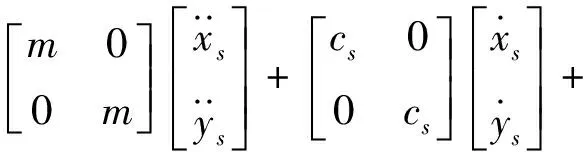
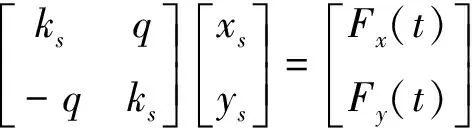
(3)

对自由振动，Fx(t)=Fy(t)=0。此时，令Zs=xs+jys，则上式可写为：

(4)

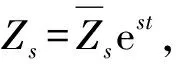
ms2+css+(ks-jq)=0

(5)

解方程，得s为：

(6)

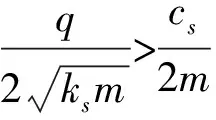
(7)

由此可见，要提高转子系统稳定性，有三个基本技术途径：①降低交叉刚度，如在平衡盘密封处用反旋流装置，在口环气封处用止涡装置等；②增加阻尼，如采用蜂窝密封、孔式阻尼密封、挤压油膜阻尼器等；③提高临界转速，如设计时增加转子直径等。改变机械结构降低交叉刚度及增加阻尼有一定能力极限，而增加转子直径提高临界转速会降低离心压缩机效率。因此增加控制元件，采取主动控制降低交叉刚度、增加阻尼具有重要工程意义。

1.2 转子失稳工程案例分析

图2为离心压缩机解体后实物图。该压缩机自投用始一直未达设计额定负荷，且在运行过程中，气体组分、流量、转速等稍微波动，均会使振动瞬间增大而致联锁停车。由于未达设计最佳工况，长期工作在低效中，可靠性亦不得保证。图3为该压缩机转子结构示意图。由图3看出，该压缩机转子共安装9级叶轮、1个轴向推力平衡盘、推力盘及驱动联轴器，其中8级用于压缩新鲜气体，最后1级用于压缩来自合成塔的循环气体。轴承跨距1 458.5 mm，转子总长1 705 mm，转速11 120 r/min。图4为振动监测频谱分析图。由图4看出，该转子振动存在较大1倍频、1/2倍频及少量低频。通过该振动值随工况变化关系可判定转子故障为失稳。

图2 故障压缩机实体图

1.3 系统稳定性随转速影响

为研究上述离心压缩机故障机理，建立转子动力学模型见图5。该模型由25个节点、24个考虑剪切效应与陀螺效应的梁单元组成。径向轴承位于6、22节点处。叶轮及平衡盘用集中质量代替。在靠近转子质心处节点14作用1000 g.mm不平衡量及施加一等效弹簧模拟叶轮及口环交叉刚度效应，交叉刚度值7500 N/mm。节点18为平衡盘、循环段所在位置，即控制器施加故障自愈力部位。

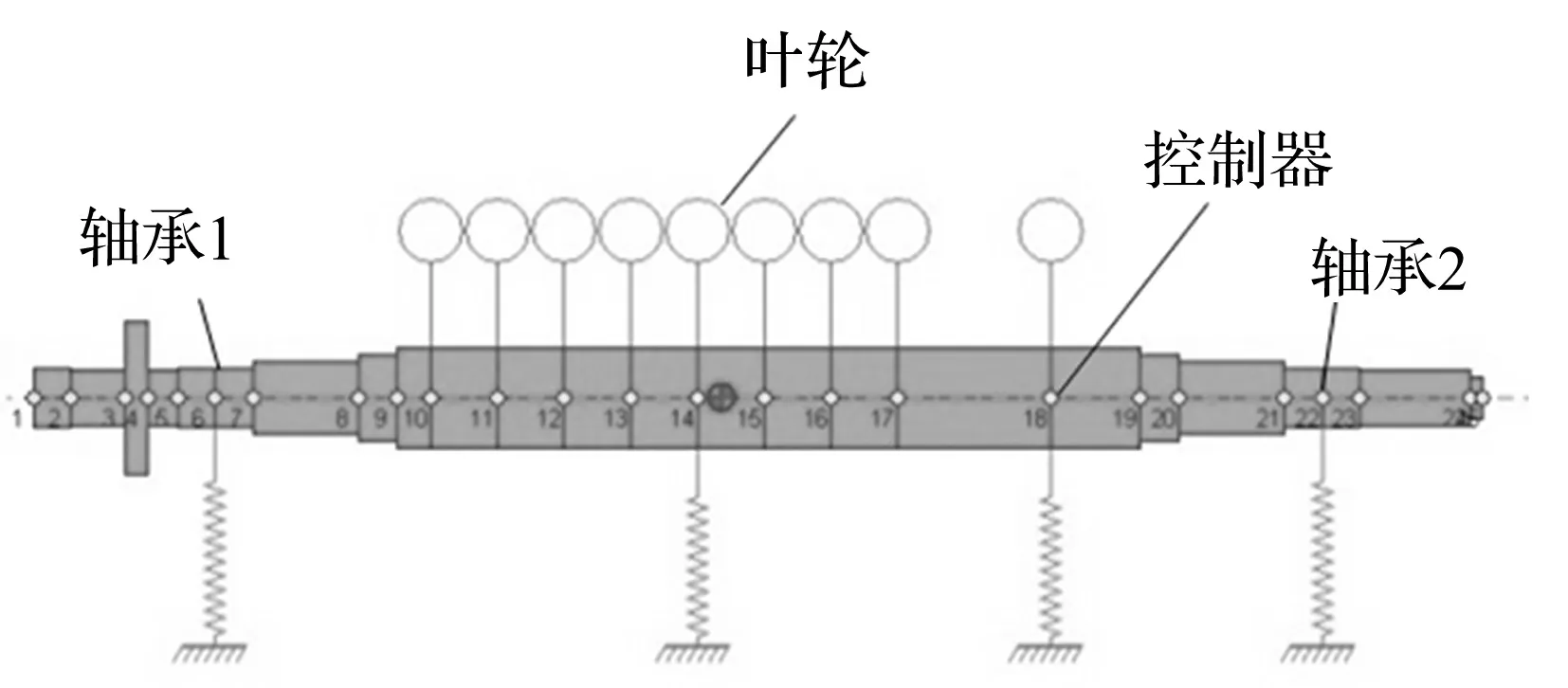
图5 故障压缩机转子动力学模型

支撑轴承为5瓦可倾瓦轴承，周围宽度40 mm，轴颈间80 mm，半径间隙0.08 mm，预负荷0，瓦块支点偏心比50%。瓦块包角57°。载荷垂直向下作用于瓦上。本文运用商业转子动力学软件Dyrobes_Bperf通过二维计算流体力学方法，用小扰动法求解线性化刚度及阻尼系数。轴承刚度、阻尼系数随转速变化关系曲线见图6。由图6看出，随转速的升高，轴承阻尼系数下降，主要因转速升高，油膜粘性剪切作用增强，温度升高所致。

图6 压缩机轴承刚度阻尼系数

转子运行过程中，作用于转子的力Fkcross及Fexcite分别为：

(8)

(9)

用Lung-kutta法，对该有限元模型进行瞬态响应分析，时间步长1E-5 s，积分得振动响应见图7(a)，当转子转速为10500 r/min时，其振动随时间的推移逐步增大，增大速度取决于系统阻尼比。对振动信号进行FFT分析可得频谱成分。振动随转速变化关系见图7(b)，由此图看出，随转速的升高，转子开始出现低频振动。转速进一步升高，通频振动幅值基本不变且频率增加，而低频振动则幅值急速升高，而频率锁定在转子一阶临界转速处。

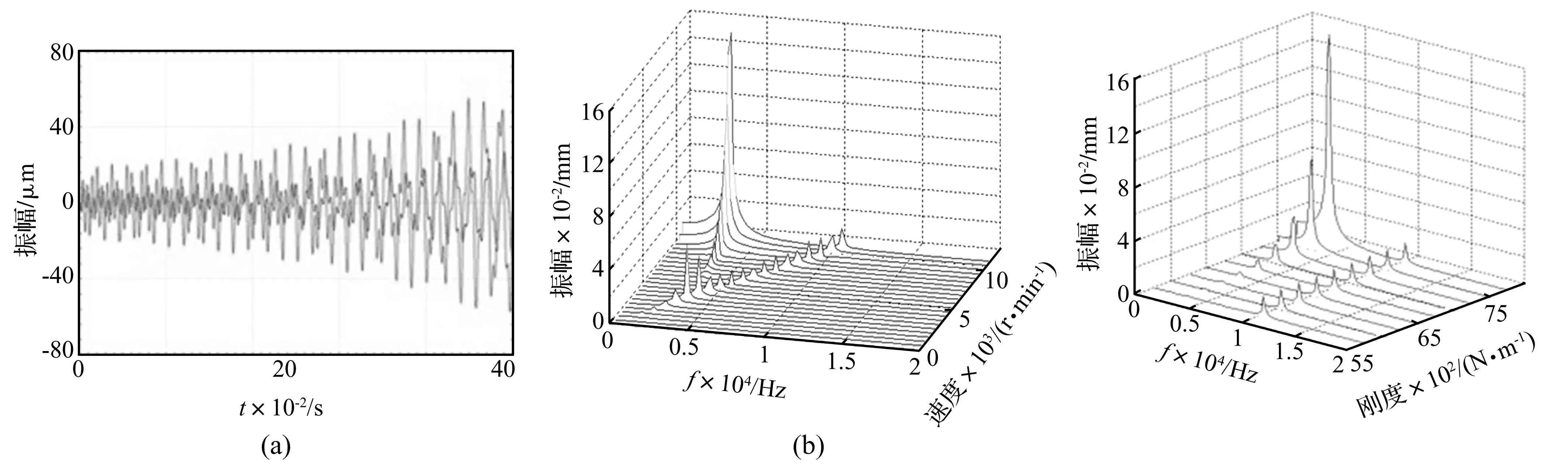
图7 不同转速振动变化图

1.4 转子系统稳定性随交叉刚度影响

作用于转子的交叉刚度受压缩机内介质组分、压力、压比及密封结构影响。转子振动随交叉刚度q变化关系见图8。由图8看出，q<6 000 N/mm时，转子振动稳定，频谱分析中未见低频振动；q=6 000 N/mm时，出现少量低频振动后随交叉刚度增加，低频振动迅速增大。由此可见，作用于转子的交叉刚度对转子稳定性具有重要影响。

2 通过交叉刚度控制转子系统稳定性

对转子稳定性控制可通过控制器降低作用于转子的交叉刚度，即进行位移反馈；也可为转子系统输入阻尼进行速度反馈。

2.1 位移反馈控制方法

通过位移反馈，即通过控制器施加一同流体作用于转子交叉刚度q方向相反的交叉刚度qc，用于自愈调控的交叉刚度力FkControl为：

(10)

该控制器以两正交方向X、Y的振动信号为输入，用比例运算求出系统输出后交叉施加到Y、X方向。该比例运算系数绝对值为qc，符号与该q相反。位移反馈控制方块图见图9。

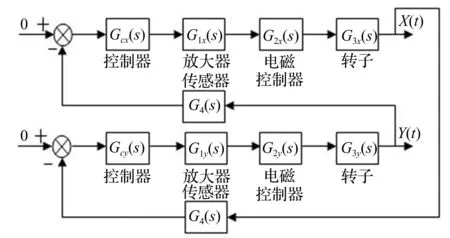
图9 位移反馈控制方块图

2.2 稳定性控制仿真结果

在不同反向交叉刚度qc=1 000 N/mm、2 000 N/mm、2 500 N/mm时的控制效果见图10。转速升高至10 500 r/min时，低频振动迅速增高。此时进行反向位移反馈，可以看出，施加反向交叉刚度后抑制转子低频振动作用明显，且随qc的增加，低频振动降低，直至消失。

图10 不同交叉刚度控制效果

本文首先求得转子振动幅值及不同控制策略下为消除振动施加给转子的控制力。通过对控制力与转子振动幅值乘积在单位时间内积分，获得不同控制策略能耗，见表1。由表1看出，通过该控制策略，可以较小功率消耗达到控制目的。

表1 不同交叉刚度能耗

3 通过交叉阻尼控制转子系统稳定性

3.1 速度反馈控制方法

该控制方法控制器以转子振动反馈为输入，对输入项做微分运算获得振动速度后乘以微分系数dc，得系统输出。该输出即用于自愈调控阻尼力FsdControl为：

(11)

速度反馈控制方块图见图11。

图11 速度反馈控制方块图

3.2 稳定性控制仿真结果

控制阻尼系数为5、10、50 N s/mm时控制效果见图12。由图12看出，为系统引入阻尼，同样能有效控制转子系统低频振动。随控制阻尼系数的增加，低频振动降低甚至消失。

图12 施加阻尼控制效果

不同控制阻尼Dc时功率消耗见表2。比较表1知，通过施加阻尼力进行转子低频振动控制，需消耗较多能量。

表2 不同阻尼的能耗

4 结 论

本文通过对一故障压缩机进行瞬态动力学分析，研究转速及交叉刚度对转子系统稳定性影响，提出基于位移反馈、速度反馈的振动控制方法，并进行仿真研究，结论如下：

(1)通过位移反馈对转子系统施加同流体激振力方向相反的交叉刚度及通过速度反馈给系统输入外阻尼均可有效控制转子系统低频振动；

(2)施加反向交叉刚度方法控制低频振动，需较少功率，更高效。

参 考 文 献

[1]Moore J W, Lewis D W, Heinzman J. Feasibility of active feedback control of rotordynamic instability[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1980.

[2]Lewis D W, Moore J W, Bradley P L, et al. Vibration limiting of rotors by feedback control[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1982.

[3]Bradfield C D, Roberts J B, Karunendiran R. Performance of an electromagnetic bearing for the vibration[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1986.

[4]Palazzolo A B, Kascak A F, Lin R R,et al. Piezoelectric pusjers for active vibration control of rotating machinery[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1988.

[5]Ulbrich H, Althaus J. Hydranlic actuator system for rotor control[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1990.

[6]Wurmsdobler P, Jorgl H P, Springer H. State space adaptive for a lumped mass rotor excited by nonconservative cross-coupling forces[C]. NASA Conference: Rotordynamic Instability Problems in High-performance Turbomachienry, Texas, USA, 1996.

[7]汪海航,汪希萱. 电磁阻尼器多频数字控制器的研究[J]. 振动工程学报,1995(2):172-177.

WANG Hai-hang, WANG xi-xuan. Studies on multi-frequence digital controller of electromagnetic damper[J]. Journal of Vibration Engineering,1995(2):172-177.

[8]Skladanek Y, Hagopian J D, Mahfoud J. Energy cost assessment of the active control of a rotating machine by using an electromagnetic actuator and a piezoelectric actuator[C]. Proceedings of ASME Turbo Expo 2009: Power for Land, Sea and Air.GT2009-59625. Orlando, Florida, USA,2009.

[9]Ei-Shafei A, Dimitri A S. Controlling journal bearing instability using active magnetic bearing[J].Journal of Engineering for Gas Turbines and Power,2010,132:1-9.

[10]Mahfoud J, Hagopian J D. Fuzzy active control of flexible structures by using electromagnetic actuators[J].Journal of Aerospace Engineering, 2011,24:329-337.

[11]刘淑莲,郑水英. 改进式被动电磁阻尼器及其应用[J].振动与冲击, 2011,30(9):94-97.

LIU Shu-lian,ZHENG Shui-ying. Improved passive electromagnetic damper and its application[J]. Journal of Vibration and Shock, 2011,30(9):94-97.

[12]祝长生,钟志贤. 带主动电磁阻尼器的裂纹转子系统动力学[J]. 振动工程学报,2012,23(3):298-304.

ZHU Chang-sheng,ZHONG zhi-xian. The dynamics of a cracked rotor with active magnetic dampers[J]. Journal of Vibration Engineering, 2012, 23(3):298-304.