阶次分析方法用于减速器故障诊断

朱春吉, 孙美玲, 岳晓峰

(长春工业大学 机电工程学院， 吉林 长春 130012)

阶次分析方法用于减速器故障诊断

朱春吉, 孙美玲, 岳晓峰*

(长春工业大学 机电工程学院， 吉林 长春 130012)

应用重采样的阶次分析技术进行减速器的输出特征值选取，并在LABVIEW中进行了振动和转速信号的仿真计算。频谱图和阶次谱图仿真对比结果验证了阶次分析方法的可行性和优越性。

阶次分析; 重采样; 减速器

0 引 言

在机械的操作应用中，减速器承担着变速、变向和动力传递的主要作用，由于通常在高速或者重载荷的情况下工作，就会经常发生故障，如齿轮的点蚀、折断、轴承内外圈的损伤、轴的弯曲或不对中等[1]。因此对减速器进行在线实时的监测和故障诊断具有非常重要的意义。对于减速器状态检测和故障诊断的有效方法之一就是振动分析法。

在常速下反应减速器的大体状态只需要运用普通频谱分析方法即可[1]。但在许多减速器应用场合中，随着转速的变化，机械特性也随之发生变化，而且只有转速达到或超过临界转速时有些机械振动缺陷才能获得[2-3]。因此，在升速或降速的情况下测试机械的振动特性成为其必要条件。但是，当转速变化时，每个独立谐波的频带变宽，频率分量就重叠了，传统的FFT功率谱图变得模糊不清，不能用以鉴别特征振动分量[4]。为解决这一问题，想要获得不随转速变化的平稳的振动信号就必须将等时间间隔采样的振动信号转变为等角度间隔来进行采集[4]。文中采用基于振动信号重采样的阶次分析软件方法，该方法硬件成本低，结构系统简单，只需要一般的转速编码器和振动传感器就可以获得信号。

1 阶次分析

1.1 FFT分析

傅里叶变换是将信号从时域转换至频域[5]。对离散信号的傅里叶变换采取傅里叶级数形式：

(1)

(2)

1.2阶次分析的过程

阶次分析过程的最关键之处是信号的重采样。通过数据采集卡和传感器可以得到在转速变化情况下等时间间隔的采样点。但由于转轴在变速的状态，所以，这些采样点并不是等角度间隔，必须通过重采样使采样点以等角度间隔的形式出现。而由编码器所测得的数组，代表了每个脉冲对应的时刻，即记录了转轴在非匀速过程中转过相同角度所用的不同时间[6]。振动信号和转速信号同步采集，由编码器所测得的数组值就可以确定在振动信号中需要插值的位置，根据time数组中提供的时刻，在振动信号的相应时刻得到插值振动值。经插值得到新振动信号序列后，这些信号就以等角度间隔表达了。对重采样后的信号进行FFT功率谱计算，将信号分析尺度由频率-幅值转变为阶次-幅值[7]。在数据采集方面，传统阶次分析只需要获得减速器振动信号即可，而基于重采样的阶次分析需要准确及同步的获得振动及转速信号[7]。振动信号重采样流程如图1所示。

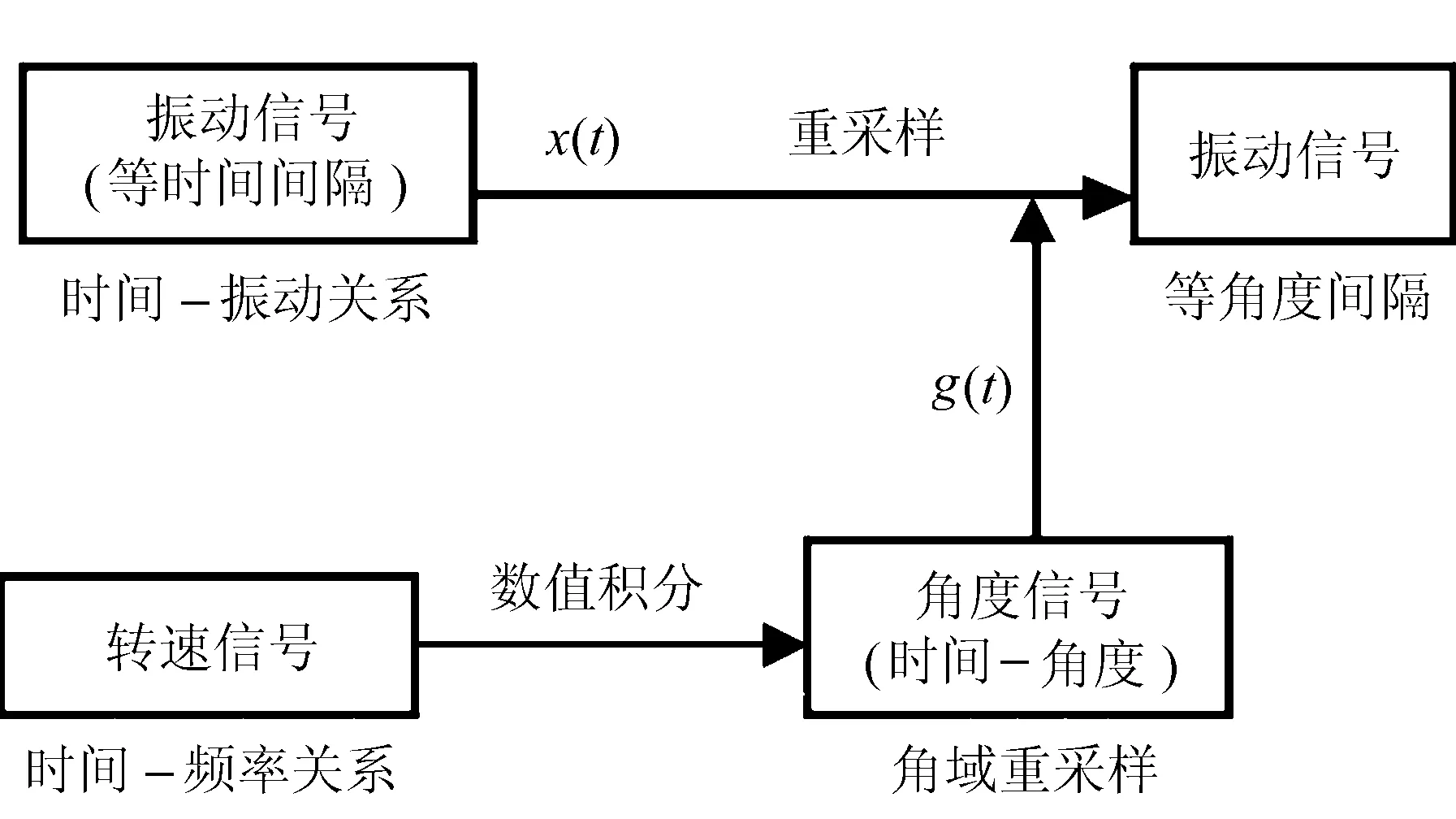
图1 振动信号重采样流程

1.3阶次分析算法的实现

编码器测量可以得到输入轴等角度间隔所对应的时刻t(θ)。由于输入轴的转速是未知的，因此需要做一定的假设。假设输入轴的转速在某一小的角度间隔内是按照时间的n次方的规律变化

(3)

式(3)覆盖了输入轴转速时匀速、匀加速、线性加速及非线性加速的变化规律。为兼顾精度及计算的效率，取n=3[4]。因此

θ(t)=a0+a1t+a2t2+a3t3

(4)

式中:ti----转速传感器输出的第i个脉冲所对应的时间；

θ----时间间隔[ti,ti+3]内转角的增量；

t----时间间隔[ti,ti+3]内时间的增量。

当t=0时，θ=0，即a0=0。因此a1,a2,a3为待定系数。连续到达的4个脉冲所对应的时间为：

(5)

它们所对应的转角序列分别为：

(6)

将式(5)和式(6)代入式(4)得

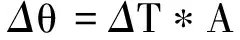
(7)

其中

因此，可以得到

(8)

因此得到在[θi,θi+3]角度范围内由角度增量反求时间增量的关系

(9)

在[θi,θi+3]内进行等角度细分，角度间距为Δθ，则Δθ为角度域的分辨率，Δθ越小，则阶次分析的范围就越大。依次在各个[θi,θi+3]内进行细分直到在整个角度域内完成。将每个细分的角度按上式进行重采样得到等角度间隔的信号序列θ(n)，n=1,2，…，N,N为采样点数。对稳态信号θ(n)进行傅里叶变换得到阶次谱ord_θ(m)为

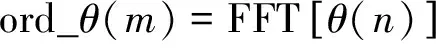
(10)

其中m的单位为(次/rad)。

上面简单介绍了FFT分析和阶次分析的原理及方法，但两者也存在一定的关系，也就是频率和阶次的关系：

(11)

(12)

式中:f----频率；

Order----阶次；

n----转速,r/min。

2 算例仿真

当减速器输入轴的转速变化时，振动的基频会变化，从而使每个独立谐波的频带变宽。由于在转速的变化下，独立频带带宽变宽，一些频率分量就重叠了。普通频谱分析的功率谱由于重叠变得模糊，所以就不能鉴别特征振动分量。

在转速为500 ～3 000r/min的升速情况下，通过模拟减速器的振动信号，观察了常用谱分析方法的效果，其信号构成见表1。

表1 模拟信号频率组成

振动信号和转速信号如图2所示。

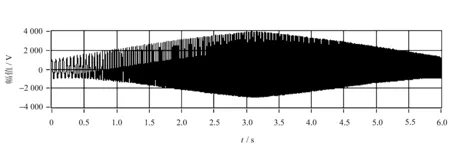
图2 振动信号

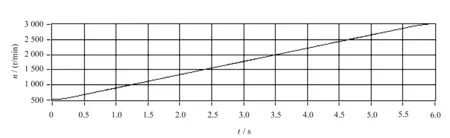
图3 转速信号

在变速情况下，随时间的变化频率或振幅也随之发生变化，相应的频带宽度就会变宽。当机械零件对应的频率范围变宽，相应的谐波频率也会变宽。谐波在变宽后就会导致常规功率谱中的频率混叠，从而不能从中区分特定的谐波分量[8]，如图4所示。

因此在转速变化的情况下，由于频带变宽而相互混叠，常规功率谱分析不能有效地分离出特征频率，难以获取有效的信息[9-10]。

基于重采样的阶次分析方法，把功率谱图的纵坐标由频率转换为阶次，虽然减速器的转速发生了变化，但是在图中其谱图的峰值并未随转速变化，始终维持在2，4，20阶处，与开始设定的情况完全一致。其特征分量的频带宽度也一直保持稳定，在转速变化的情况下，带宽没有发生变化，也就说明了没有频率混叠的情况出现，把变速过程的频谱分析视同匀速过程，如图5所示。

对图2中信号进行常规的FFT功率谱分析，可以看出，在其转速增大的情况下，常规的功率谱不能对周期分量进行表达，如图6所示。

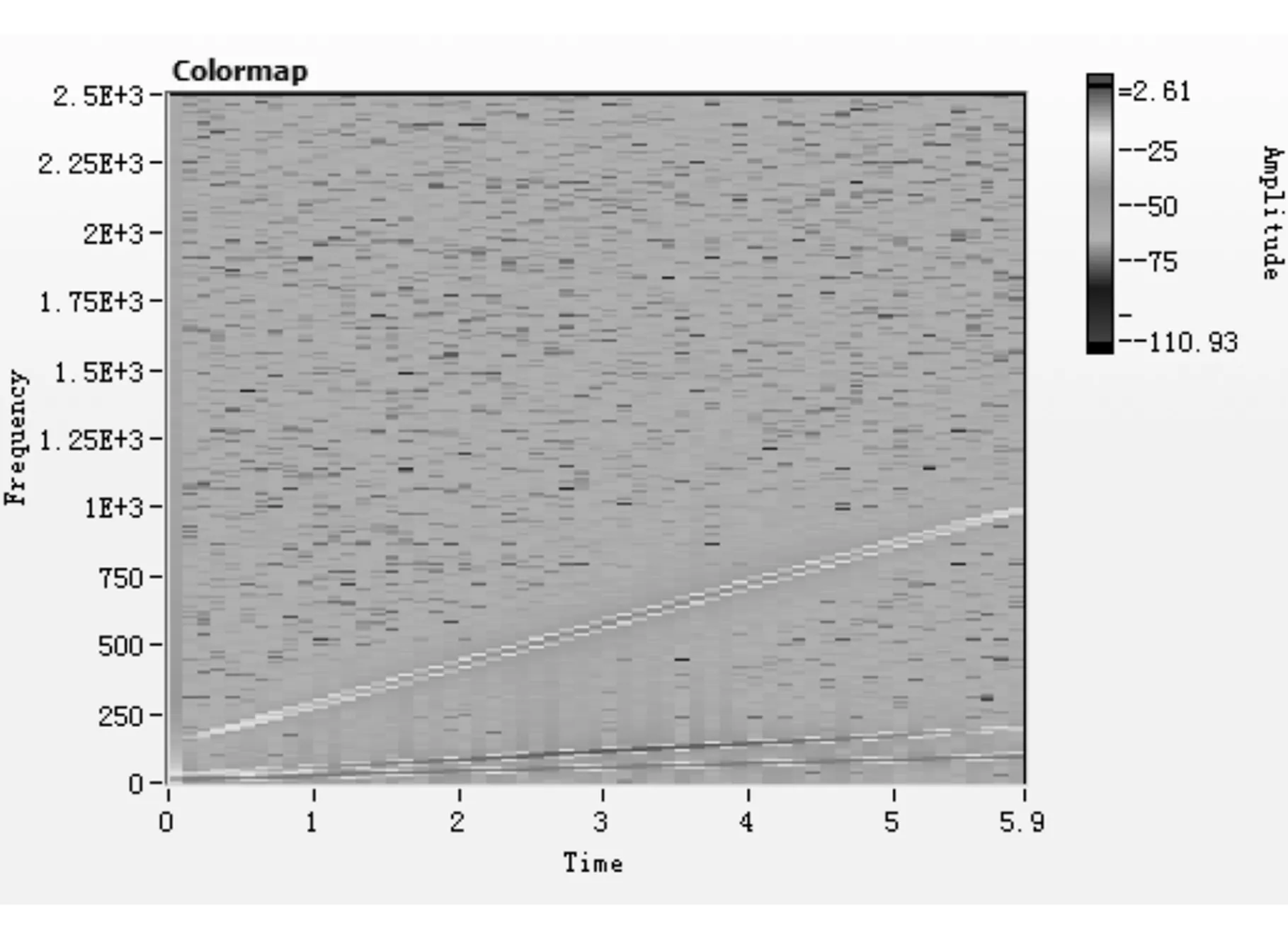
图4 变速过程功率谱强度图

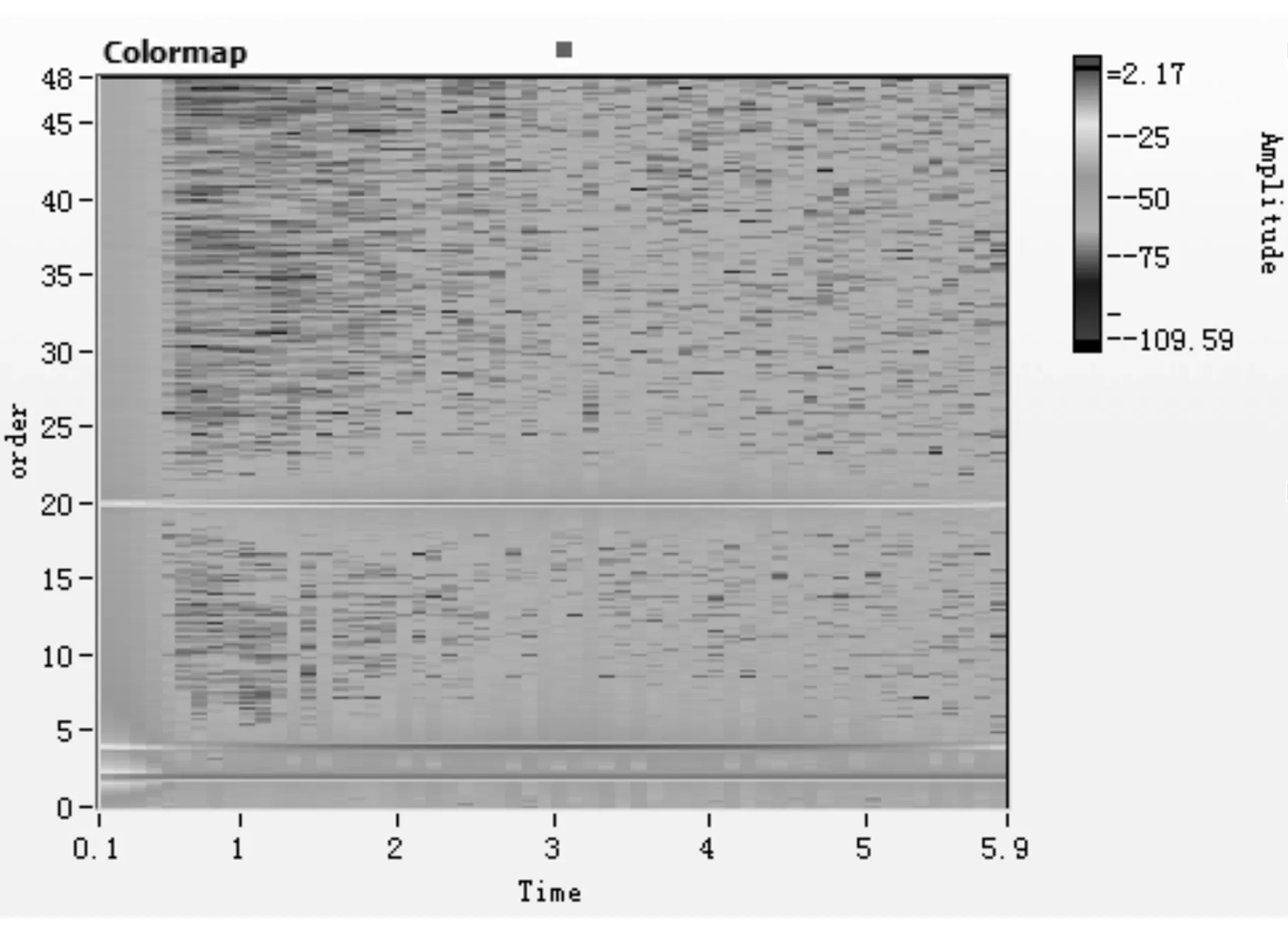
图5 阶次分析强度图

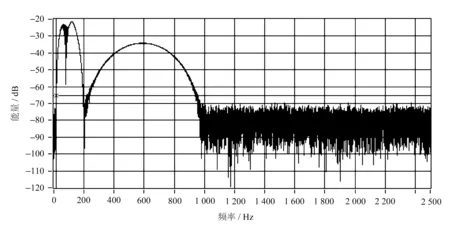
图6 变速情况FFT功率谱

振动信号经重采样后，表达的单位由频率变为阶次，能够看出转轴的基频倍数出现在2，4，20阶处，由此证明基于重采样的阶次分析更具优越性。变速情况阶次功率谱如图7所示。

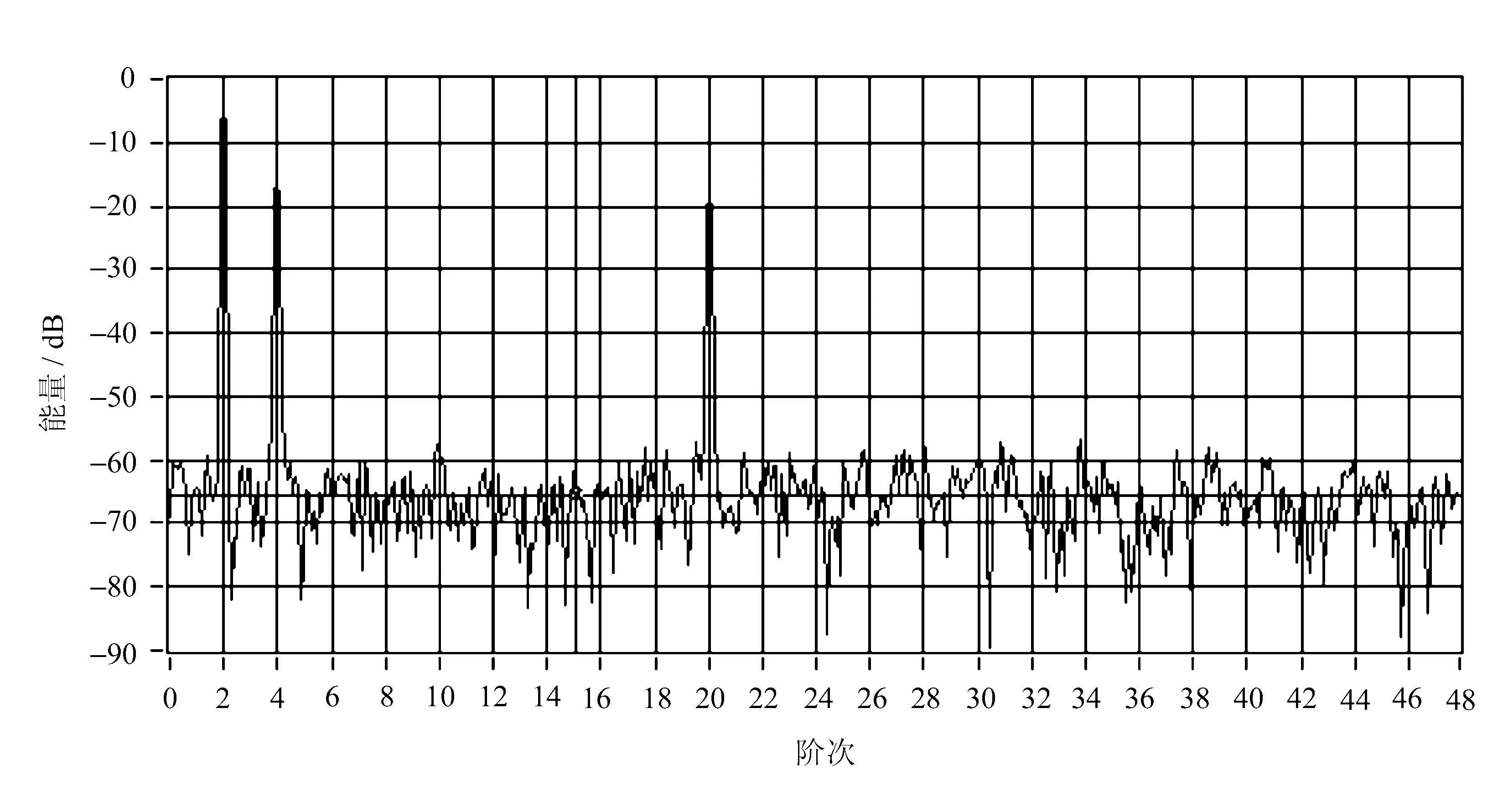
图7 变速情况阶次功率谱

3 结 语

根据3次多项式拟合在短角度范围内角度变化的规律，把时域的非平稳信号转化为角度域的稳态信号，就能更好地反映和转速有关的信息。通过对比传统频谱图和阶次谱图,验证了阶次分析的可行性和优越性，证明了阶次分析方法对减速器的转轴及啮合齿轮上出现的故障特征具有明显的识别作用。

[1] 丁康，朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京：机械工业出版社,2005.

[2] 陈恩伟，刘正士.齿轮箱故障诊断的阶次分析方法的研究[J].仪器仪表学报,2008，29(4):239-242.

[3] 张力.基于labview的旋转编码器转角及转速测量仪的设计[J].三峡大学学报,2008,30(3):68-70.

[4] 蒋青松，谢庆年.基于labview的旋转机械阶比分析[J].武汉理工大学学报,2011，33(3):418-420.

[5] 汪伟，杨通墙.非稳态信号计算阶次分析中的重采样率研究[J].振动、测试与诊断,2009，13(5):678-680.

[6] 李联玉.汽车变速箱在线性能检测及声振控制的应用研究[D]：[硕士学位论文].大连：大连理工大学，2004.

[7] 粱锋.通用性齿轮箱状态监测与故障诊断系统的研究[D]：[硕士学位论文].重庆：重庆大学，2004.

[8] 朱元佳，万德安.汽车变速箱在线快速故障诊断技术研究[D]：[硕士学位论文].上海：同济大学，2007.

[9] 王远成，万德安.阶次分析在齿轮变速箱故障诊断中的应用[D]：[硕士学位论文].上海：同济大学,2006.

[10] 孙美玲，朱春吉，岳晓峰.时域同步平均在振动信号分析中的应用[J].长春工业大学学报:自然科学版，2014，35(4)：398-401.

Order analysis applied in fault diagnosis of retarder

ZHU Chun-ji, SUN Mei-ling， YUE Xiao-feng*

(School of Mechatronic Engineering, Changchun University of Technology, Changchun 130012， China)

Re-sampling order analysis method is used to choose the eigenvalues of a retarder, and simulation calculations in LABVIEW is carried for both vibration and speed signals. The comparison results between the traditional spectrum and order spectrum verify the feasibility and superiority of the order analysis methods.

order analysis; re-sampling; retarder.

2013-10-20

吉林省科技厅支撑项目(20110303)

朱春吉(1988-)，男，汉族，吉林长春人，长春工业大学硕士研究生，主要从事机械制造及其自动化方向研究,E-mail:398042455.qq.com. *联系人：岳晓峰(1971-)，男，汉族，吉林长春人，长春工业大学教授，博士，主要从事机械制造及其自动化方向研究,E-mail:yuexiaofeng@mail.ccut.edu.cn.

TP 391

A

1674-1374(2014)05-0547-05