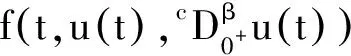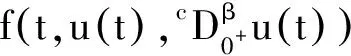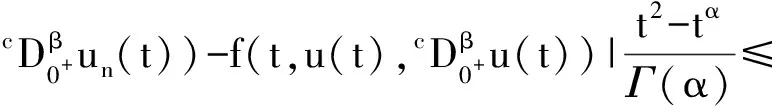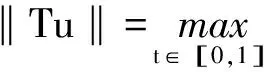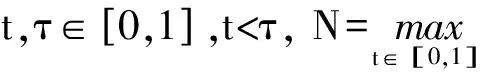分数阶为2<α≤3的微分方程两点边值问题解的存在性
葛 碧,王 培,徐艳艳
(1.重庆师范大学涉外商贸学院数学与计算机学院,重庆 合川 401520;2.西华大学数学与计算机学院,四川 成都 610039)
近年来,随着分数阶微分方程在工程、经济等众多领域的重要应用,此问题的研究亦受到众多学者的关注。研究分数阶微分方程及分数阶微分方程的边值问题对解决非线性问题意义重大。
本文主要研究以下边值问题:
(1)
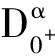
1 预备知识
定义1[1]函数f:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为
其中:α>0;Γ(α)为Gamma函数,右端在R+上逐点有定义。
定义2[1]函数f:(0,+∞)→R的α阶Riemann-Liouville分数阶导数为:
其中n=[α]+1,[α]表示α的整数部分,右端在R+上逐点有定义。
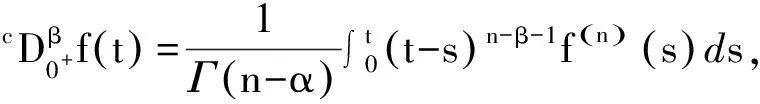
其中n-1<β 本文的主要结果证明将用到以下3个引理。 其中,cj∈R,j=1,2,…,n。n是满足n≥α的最小整数。 引理2 若u(t)∈C[0,1],分数阶边值问题 (2) 结合Riemann-Liouville分数阶积分的定义可有 则边值问题(2)的唯一解可以表示为 在这里, 则函数|G′(t,s)|是t∈[0,1]上的可积函数。 我们考虑 故分数阶边值问题(1)有解等价于算子方程Tu=u有不动点(这里只考虑0<β<1的情况)。 C[0,1]表示[0,1]上全体连续函数,其范数定义为 易知(X,‖·‖X)是Banach空间。 引理3[1]设X是一个Banach空间,U⊂X为非空有界凸子集,又设T:U→U是一个全连续算子,则T在U中有不动点。 则分数阶2点边值问题(1)至少有1个解。 证明:令 令U={u(t)|u(t)∈X,‖u‖≤d,t∈[0,1]},则U是有界闭凸子集。 因此,T是连续的。 接下来,我们证明T:U→U。对任意的u(t)∈U有 因此,T是U→U的。 因为 2t2(1-t)α-1,2t2(1-τ)α-1,tα,t2,τα,τ2,4t(1-t)α,4t(1-τ)α,2t,2τ,4(t-τ)-β在[0,1]上都是一致连续的, 所以算子T是等度连续的, 又有Tu∈U, 故一致有界。 因此T是全连续算子。则由不动点定理可知,分数阶边值问题(1)在U中至少有一个解。 [1]张晓娜,胡卫敏,邱中蔚.一类分数阶微分方程两点边值问题解的存在性[J].伊犁师范学院学报:自然科学版,2012(1):5-9. [2] Xu Xiaojie , Jiang Daqing , Yuan Chengjun . Multiple Positive Solutions for the Boundary Value Problem of a Nonlinear Fractional Differential Equation[J]. Nonlinear Analysis, 2009,71:4676-4688. [3]Bai Z B, Lu H S. Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation[J]. J Math Anal Appl,2005,311:495-505. [4]Su X W, Liu L D. Existence of Solution for Boundary Value Problem of Nonlinear Fractional Differential Equation[J].App1 Math Chinese Univ Se B,2007,22(3):291-298. [5]Xu X,Jiang D, Yuan C. Multiple Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation[J].Nonlinear Analysis Series A:Theory,Methods and Applications, Nonlinear Analysis,2009,71:4676-4688.
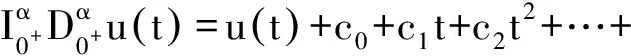

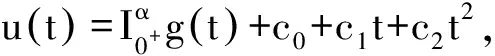

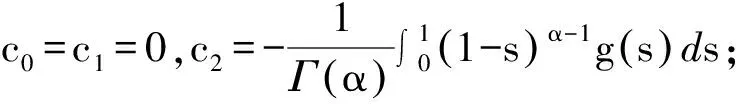



2 主要结论及证明