快速并行细化算法在焊缝识别中的实现

2014-09-04 03:50金世林

西华大学学报（自然科学版） 2014年6期

崔宣，丁杨，高文，金世林

(西华大学机械工程与自动化学院，四川成都 610039)

在一些机械零部件的生产过程中，焊接起到了十分关键的作用，其焊接质量对工件的质量有非常大的影响[1]。焊缝中出现的夹渣、虚焊、沙孔、疏松甚至偏焊漏焊等缺陷很难完全避免，所以在焊接之后焊缝的探伤工作是不可避免的。探伤需要首先找到准确的焊接部分。在欧美等发达国家，探伤的研究进行较早，且投入了大量的人力物力[2]；而我国基本上采用人工抽样探伤或者半自动设备探伤，识别错误率高、速度慢，探伤的有效性低。为此，本文提出一种基于图像快速并行细化的焊缝识别方法，以代替人工对焊缝的位置识别，该方法主要是通过图像快速并行细化算法找到焊接部分的准确位置，并指导检查设备对其进行检测，实现自动化。大部分的图像主要集中在PC环境中使用matlab实现识别，不利于嵌入式的移植。本文利用C#语言和FreeMat开发，以增强算法的可移植性，使其能够应用于一些嵌入式平台，降低自动焊接质量检测设备的价格。

1 图像处理流程

焊缝的图像识别主要经过图像的获取、图像的灰度变换、图像二值化、图像的缩放、图像的细化、图像的去除噪点、输出焊缝路径等处理步骤[3]，如图1所示。

图1 图像处理流程图

2 RGB图像转化为灰度图像

图像转换主要是将真彩色图像转变为灰度图像。其著名心理学公式[4]为

Gray=R×0.299+G×0.587+B×0.114。

(1)

对于程序的算法来说，式(1)涉及浮点运算，所以编程的效率会非常低。在实际运用中，应尽量避免低速的浮点运算而使用整数算法。

由于该算法需要32位运算，所以式(1)可变为另一种形式

Gray=(R×30+G×59+B×11+50)/100。

(2)

对于实际操作来说，式(2)会制约运算速度，所以可以将系数缩放成 2的整数幂。习惯上使用16位精度，2的16次幂是65 536，所以系数的计算为：

0.299×65536=19595.264≈19595；

(3)

0.587×65536+(0.264)=38469.632+0.264=38469.896 38469；

(4)

0.114×65536-(0.896)=7471。

(5)

由于四舍五入会有较大的误差，所以将以前计算结果的误差一起计算进去进行舍入，其表达式为

Gray(R×19595+G×38469+B×7472)≫16。

(6)

其中

Gray=(R×38+G×75+B×15)≫7。

(7)

式(7)使用了16位的位运算，其效率高，并且运算精度高，超过了前面放大100倍的运算精度。

同时式(8)也可以达到相似的效果，且运算量大大减小，所以本文采用之。

Gray=(R×1+G×2+B×1)≫2。

(8)

式(8)可以通过位运算优化为

Gray=(R+G≪1+B)≫2。

(9)

式(9)实现了无乘除法的完全移位运算优化。

在FreeMat中，由于不支持位运算，所以计算方法依然和普通乘除法相同，在此省略FreeMat的代码。C#支持位运算，并且位运算相对于乘除法运算有很大的速度优势，其代码如下。

private static uint RGBtoGray(uint r,uint g,uint b)

{uint res=g<<1;

res+=r+b;

return res>>2;}

3 图像二值化

在数字图像处理中，图像二值化占有非常重要的地位。该方法是将图像上的像素点的灰度值设置为0或255，使整个图像呈现明显的黑白效果[3,5]。

要进行二值图像的处理与分析，必须把灰度图像二值化。图像的二值化使图像变得简单，数据量减小，能凸显出感兴趣的目标轮廓。

阈值分割不仅可以大量压缩数据，减少储存容量，而且能够大大简化其后的分析和处理步骤。

设原始图像为f(x,y),在一定的准则下找出一个合适的灰度值作为阈值，按照阈值进行分割后的图像是g(x,y)，可表示为：

(10)

要实现图像的二值化首先要选择分割的阈值。常见的方法有双峰法、迭代法、大津法(即OTSU法)、直接法、固定阈值法，本文使用的是固定阈值法[3]。

经过图像灰度转换、二值化、图像分割和膨胀腐蚀等预处理过程后，接下来将对图像进行快速并行细化处理。

4 图像快速并行细化

图2为二值纹理图像中某一像素点P1的3×3邻域。设P1为纹理上的一点，其值为1，所有非纹理点取值0。细化过程为逐步迭代过程。在第n次迭代中P1的取值不但取决于P1本身的值，还取决于P1的邻域点在第(n-1)次迭代后的值。在整个纹理图像域内，所有满足条件的像素点可以同时去掉，并行算法便由此得名[4-7]。

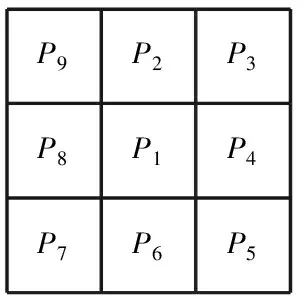
P9P2P3P8P1P4P7P6P5

图2P1的3×3邻域

为保证原纹理的连续性，每次迭代分成2个子迭代。第1次子迭代消去纹理的所有东、南边界点和西北角的点；第2次子迭代消去西、北边界点和东南角的点。

在标准的计算过程中每次迭代会标记相应的点，然后在迭代结束后删除对应的点。迭代条件如表1所示。

表1 细化算法迭代条件

其中A(P1)是按P2,P3,P4，…，P9的排列顺序出现0 1(或 1 0)模式的个数，即从P2到P9几次出现0到1(或1到0)的变化。B(P1)是P1的8邻接点中非零值的个数。

B(P1)=P2+P3+P4+…+P9。

(11)

对于条件1，B(P1)=1时，只能出现8种情况之一[4]。显然，P1是纹线的端点。为保证细化后线条不缩短，甚至被全部吞食，P1必须被保留。当B(P1)=7或B(P1)=8时，为保证消蚀是从外缘逐层向中心骨架进行，并保证细化纹线的定中性和拓扑不变性,P1必须被保留。

条件2保证了细化纹线的连续性。原始纹线只要有1个像素相连，细化后就不会出现坟线断裂。假设A(P1)=2，P1显然是纹线上不能去掉的点，否则将破坏纹线的连续性。类似的，当A(P1)=3，A(P1)=4时，情况与A(P1)=2的相似，如果去掉P1点就会破坏纹线的连续性。

对于条件3和4，只有当P4=0或P6=0或P2，P8同时等于0才能同时满足条件。当P4=0时，则表示P1为纹线的东边界点，如果去掉P1点，则可去掉整个图像所有纹线的东边界点。同理，当P6=0时，表示要去掉所有纹线的南边界点。当P2，P8同时等于0时，表示要去掉所有纹线的西北角点。

以下为FreeMat实现并行图像细化算法的过程.

首先需要判断当前点是否为前景点，若为背景点则不需要处理，细化时只是细化前景点。

if( false == tempin.getxy( tx, ty ) )

continue.

接着将当前点和8邻域的各个点按照顺序排列到数组中，用于存储数据。通过对数据储存，可以方便调试时观察数据的正误，以及后续的运算过程的处理。

//初始化8个邻域数据点

bool pt[9];

pt[0] = tempin.getxy( tx, ty );

pt[1] = tempin.getxy( tx, ty - 1 );

pt[2] = tempin.getxy( tx + 1, ty - 1 );

pt[3] = tempin.getxy( tx + 1, ty );

pt[4] = tempin.getxy( tx + 1, ty + 1 );

pt[5] = tempin.getxy( tx, ty + 1 );

pt[6] = tempin.getxy( tx - 1, ty + 1 );

pt[7] = tempin.getxy( tx - 1, ty );

pt[8] = tempin.getxy( tx - 1, ty - 1 ).

根据前文中对细化算法的说明可知，对于这9个点的顺序并不是任意分布，所以要按照顺序排布这9个点。排布好以后，通过数组索引来代替直接使用坐标读取数据。

判断这几个领域点的状况，如果8邻域中的8个点有6个及以上的点为前景时，视此点为内部点；如果仅有1个点是前景点时，则此点为孤立点。通过计算邻域点的数目，从而判断原坐标点为内部点或孤立点的情况。

int tcount = 0;

for( int tt = 1; tt < 9; tt++ )

{if( true == pt[tt] )

tcount++;}

if( tcount < 2 || tcount > 6 )

continue.

经过对内部点和孤立点的判断以后，如果不是内部点和孤立点的话，程序会继续执行，然后需要判断8邻域的分支数量，如果分支数量为1，则视此点在图像内容的边界上，可以对此点进行消除。

int tcount2 = 0;

for( int tt = 1; tt < 8; tt++ )

{if( true == pt[tt] && false == pt[tt+1] )

tcount2++;}

if( true == pt[8] && false == pt[1] )

tcount2++;

if( tcount2 != 1 )

continue.

接下来对右方和下方的像素点进行判断。如果满足条件，则删除此点；否则跳过这个循环。

bool tempb1 = false; bool tempb2 = false;

tempb1 = pt[5] && pt [7] && pt[1];

tempb2 = pt[5] && pt [3] && pt[7];

if( true == tempb1 || true == tempb2 )

{continue;}

如果以上条件均满足，则没有跳出这循环，直接进行删除点操作，并记录标记。

temp.setxy( tx, ty, true );

modified = true;

counter++.

以上过程完成了一个方向上的操作，在另外一个方向上，基本流程都一样，大部分语句都是相似的，主要的区别在于对点的条件判断进行了修改，对图2中P1点左方的像素点和上方像素点进行判断。

bool tempb1 = false; bool tempb2 = false;

tempb1 = pt[5] && pt [7] && pt[1];

tempb2 = pt[5] && pt [3] && pt[7];

if( true == tempb1 || true == tempb2 )

{continue;}

5 实验

本文对焊缝图像的2种情况进行实验：一种是直接采用焊缝图像进行处理如图3所示；另一种是对图像加上椒盐噪点后再进行处理，以检查图像的抗噪能力如图4所示。首先读取原始图像，对图像进行灰度变换，通过位运算优化后，在C#中的执行效率有一定的提升；然后对灰度图像进行缩小变化，其目的是固定处理图像的大小，确定处理的时间。其算法过程为：读入原图，计算出该图的尺寸大小，通过缩放比例得到目标图像尺寸大小；扫描X轴和Y轴方向像素点，对每个目标图像坐标(u，v),利用近邻取样法在原图中找到模块中心位置(i,j)；进行双线性插值，并对X方向和Y方向递推实现图像缩小；利用公式temp=temp+grayimg(u,v)进行递推，得到最终缩小的图像scaleimg(i,j)。

(a)原始图像

(b)灰度图像

(c)缩小图像

(d)二值化图像

(e)细化后图像

此方法相对于临近取样法有更好的图像效果，但是运算速度相对较低，适合一些小规模的数据。由于处理的是固定大小的图像，这种缩放方法的运算量是一常量，所以这种方法是合理的。

在图像二值化后，图4(d)中的焊缝占有几个像素宽度，但通过细化处理以后都变成了一个像素宽度的点，这说明图像细化方法有一定的缺点，在有些特殊情况的地方会出现一个像素的断点。解决这个问题的方法是通过其他细化算法得到更加精确的没有断点的图像；但是对于焊缝的轨迹来说，由于焊缝都是比较长的直线，若是出现了一个像素的断点，可以通过后期的软件插补出对应的直线轨迹，所以这种断点对于实际应用来说几乎是没有影响的。在图4焊缝加噪点处理过程中，原始图像被人为添加了椒盐噪点，图像本身受到很大影响，通过缩小方法后依然有许多噪点，通过图像二值化以后，噪点依然存在。