非负矩阵Hadamard积的最大特征值的上界

(电子科技大学数学科学学院，四川 成都 611731)

非负矩阵是在理论和应用2方面都非常重要的矩阵，尤其是非负矩阵的最大特征值相关问题一直是矩阵理论研究的热点之一。本文给出了非负矩阵Hadamard积的最大特征值的上界的新估计。

1 预备知识

为了方便，给出如下定义。

定义1[1]如果A中任意元素aij≥0，则称A=(aij)为非负矩阵。

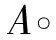
定义3[3]设A∈Rn×n，则称A是不可约的或存在置换矩阵P，使得

其中Ai是不可约的，i=1,2,…,k。

最近很多学者研究了关于非负矩阵Hadamard积的最大特征值的上界估计问题，例如和本文相关的文献[4]和[5]得到了下面的结果。

定理1[4]设A=(aij)∈Rn×n和B=(bij)∈Rn×n均为非负矩阵，则

aiiρ(B)-biiρ(A)}

(1)

定理2[5]设A=(aij)∈Rn×n和B=(bij)∈Rn×n均为非负矩阵，则

(2)

2 主要结果及证明

这部分内容主要给出了非负矩阵Hadamard积最大特征值的上界的新估计，并给出了比较结果。为了得到新结果，给出如下引理。

引理1[1]设A≥0为n阶不可约矩阵，则

1)A有一个正实根等于它的谱半径；

2)A有一个对应于特征值ρ(A)的特征向量x>0。

引理2[4]设A、B为n阶复矩阵，如果E、F为n阶对角矩阵，则

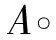
引理3[6]如果A为不具有零行的非负矩阵，其中γi(A)表示矩阵A的第i行元素的绝对值之和，对任意的具有正对角元的对角矩阵D，有

引理4[1]设A=(aij)∈Rn×n为非负矩阵。如果Ak是A的主子矩阵，有ρ(Ak)≤ρ(A)。如果A是不可约的且Ak≠A，有ρ(Ak)<ρ(A)。

引理5[3]设A= (aij)∈Cn×n，(n≥2)，Ri表示A的第i个行盖尔圆半径。如果λ是A的特征值，则存在正整数对(r,q)且r≠q(1≤r,q≤n)，使得

|λ-arr|·|λ-aqq|≤RrRq

定理3 设A=(aij)∈Rn×n和B=(bij)∈Rn×n均为非负矩阵，则

(3)

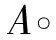
ρ(A)>aii,∀i∈N;ρ(B)>bii,∀i∈N。

因为A=(aij)和B=(bij)均为非负不可约的，由引理1，则存在2个正向量u、v满足Au=ρ(A)u，Bv=ρ(B)v。则有：

令D=VU，通过引理2，对任意的正对角矩阵D，有

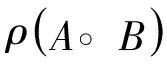
通过引理5，存在正整数对(i,j)(i≠j,1≤i,j≤n)，满足

(4)

由(4)式，推出

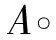
下面比较不等式(1)和(3)，不失一般性，对i≠j，假设

aiibii+ajjbjj+[(aiibii-ajjbjj)2+

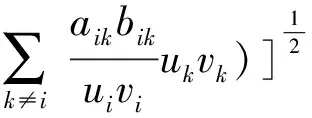
(5)

又因为

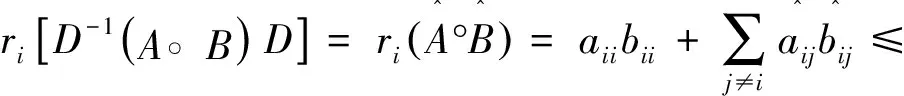
(6)

由 (5) 式和(6)式我们能得到

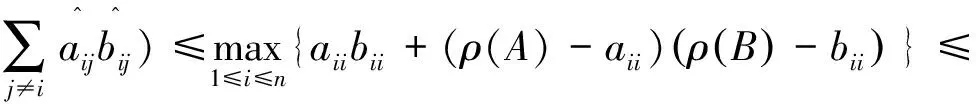
所以，(3)式的界要比(1)式的好。下面对(2)式和(3)式作比较，容易得到

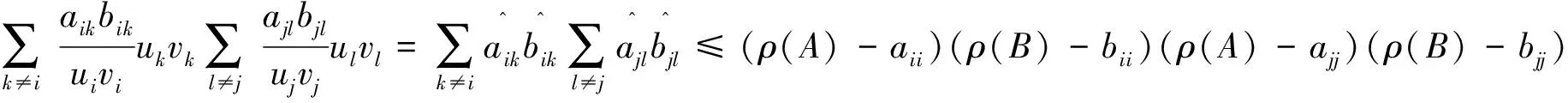
由此可见(3)式的界要比(2)式的界好。但是，由于(3)式需要知道非负矩阵A和B的Perron向量使得计算量可能比较大，这是(3)式的不足之处。

3 数值例子

直接计算得

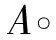
由(1)式得

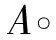
由(2)式得

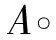
由(3)式得

这个例子说明(3)式得到的界比(2)式和(1)式更加精确。

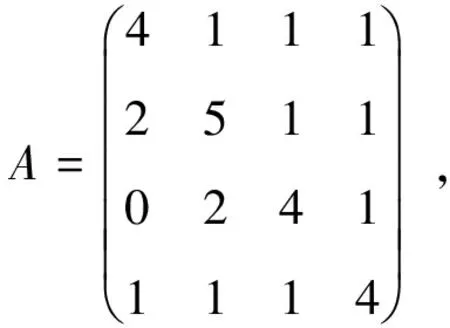
直接计算得

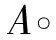
由(1)式得

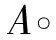
由(2)式得

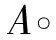
由(3)式得

ρ(A°B)≤21.136 2

这个例子也能说明(3)式得到的界比(2)式和(1)式更加精确。

[1] 黄庭祝，杨传胜. 特殊矩阵分析及应用[M].北京：科学出版社，2007:47.

[2]Li Y T,Li Y Y, Wang R W, et al. Some New Bounds on Eigenvalues of the Hadamard Product and the Fan Product of Matrices[J]. Linear Algebra Appl, 2010, 432 : 536-545.

[3]Zhou D M , Chen G L , Wu G X , et al. On some New Bounds for Eigenvalues of the Hadamard Product and the Fan Product of Matrices[J]. Linear Algebra Appl, 2012, In Press.

[4]Liu Q B , Chen G L. On Two Inequalities for the Hadamard Product and the Fan Product of Matrices[J].Linear Algebra Appl, 2009, 431: 974-984.

[5]Liu Q B , Chen G L, Zhao L L.Some New Bounds on the Spectral Radius of Matrices[J]. Linear Algebra Appl, 2010,432:936-948.

[6]Kolotilina L Y. Bounds for the Perron Root, Singularity/ Nonsingularity Conditions, and Eigenvalue Inclusion Sets[J]. Numer Algorithm ,2006 ,42 : 247-280.