改进遗传算法在导热反问题研究中的应用——以建筑物外墙热工参数协同研究为例

*

(1.四川大学建筑与环境学院,四川 成都 610065 2.上海海洋大学海洋工程研究所，上海 201306)

从传热学的角度出发，建筑围护结构的热工性能直接影响着建筑物的耗热量和耗冷量(即建筑物的能耗)。热工性能参数有传热系数、热阻、遮阳系数、热惰性指标等，各参数之间相互作用，共同决定建筑物能耗的大小。国内外的许多学者就热工性能参数对建筑物能耗的影响作了大量的研究[1-6]。目前绝大多数的研究采用的是单因素分析法，通过改变其中的一个参数变量来研究其对建筑物能耗的影响效果，即知单因求果，采用传热学中导热正问题的方法可以很容易求解。如果以给定的建筑物外墙温度场或通过墙体的热流密度之和(即能耗)为控制目标，分析墙体多参数之间的协同关系，即知果寻多因，属于多因素求解问题范畴，用传热学中传统的理论方法求解将无法进行，需要引入导热反问题的方法进行求解。导热反问题主要有3大类:边界热流重构问题、热物性参数估计问题和内热源识别问题。国内外对于前2类导热反问题的求解方法研究较多，如共轭梯度法、正则化方法、正交基函数法等。智会强等[7]提出了用遗传算法进行热物性的参数识别方法，取得了较好的效果。

本文将遗传算法在导热反问题中的应用加以拓展，以多层墙体的稳态导热反问题为研究对象，采用改进的遗传算法，结合数值计算方法建立完整的数学模型，以建筑物墙体一定的温度场或热流密度作为约束条件，对多层墙体的多个参数取值进行数值反演计算，探寻各参数间的相互协同关系，拟解决知果求多因问题，为建筑节能中的类似研究探寻一条可行之路。

1 参数协同概念的提出

图1 三层墙体一维稳态传热温度分布

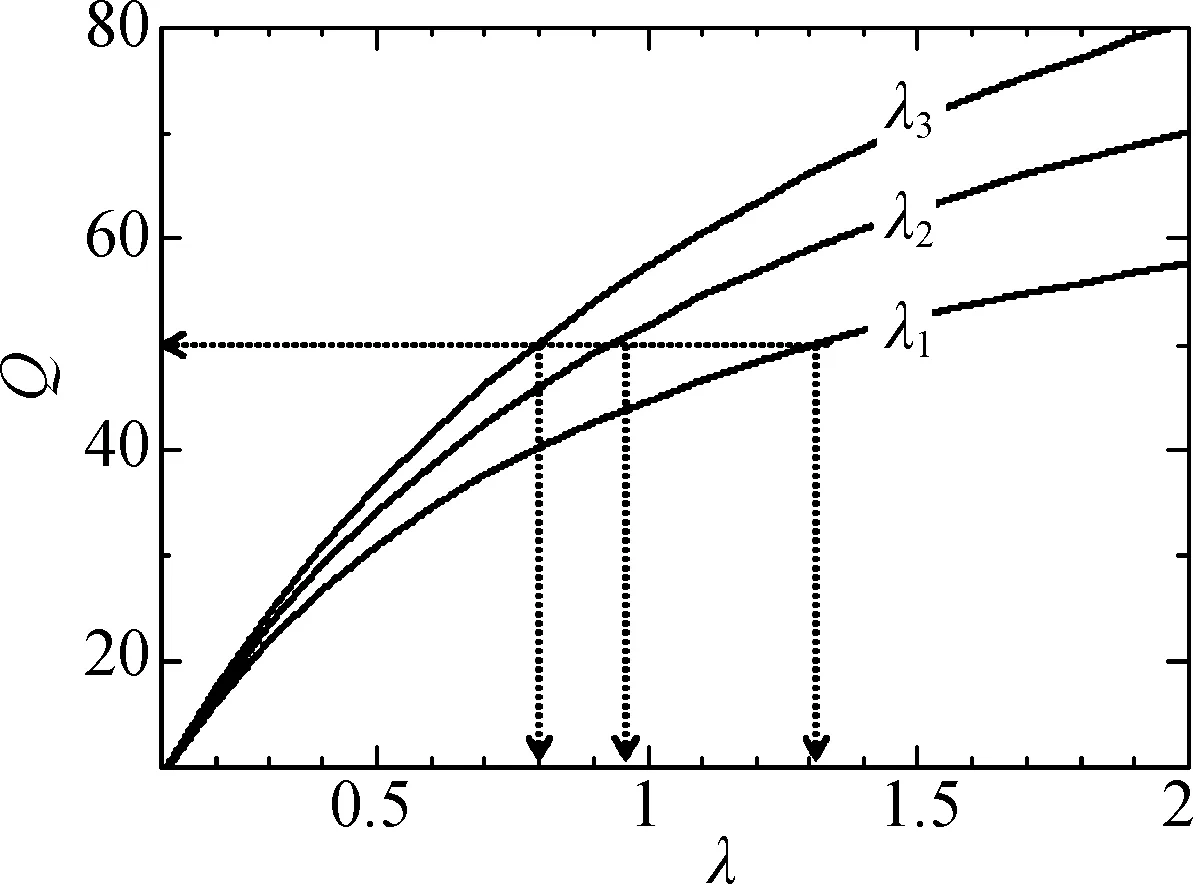
图2 三层墙体非稳态传热量与导热系数的关系

本文拟以建筑外墙一维稳态导热反问题中的参数协同问题为研究对象，通过数值计算和改进遗传算法相结合的数学模型进行外墙多参数之间的协同研究。

2 数值计算方法

2.1 数学模型

对于一维稳态导热，其基本控制方程为

(1)

边界条件为第一类热边界条件：

T|x=0=T1

(2)

T|x=L=T2

(3)

式中：T1、T2分别为墙体外侧和内侧壁面的温度；d1、d2、d3分别为三层墙体各层的厚度。

2.2 计算方法

本文采用有限差分法对控制方程进行离散，网格节点设置如图3所示。

将离散后的控制方程及边界条件应用TDMA方法求解，采用FORTRAN编写程序计算，即可得到墙体内部的温度分布及热流密度。

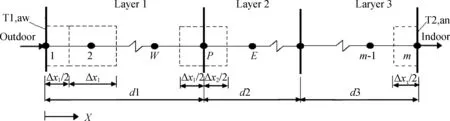
图3 三层墙体网格节点划分示意图

3 改进的遗传算法简介

遗传算法主要由选择、交叉、变异3个基本算子组成。其中交叉操作是遗传算法的主要进化手段。为了获得有效的交叉操作，本文采用了相关性配对方法，从而避免近亲繁殖。在进行交叉操作时，采用了一多点交叉算子，确保交叉操作能产生新的个体。对新产生的种群与父代种群引入竞争机制，择优录取较优个体构成下一代种群。

3.1 相关性配对

3.1.1 不相关性指数

文献[9]提出了个体相关性的概念，相关性是指2个个体之间的相似程度。

定义个体X、Y之间的不相关性指数为：

(4)

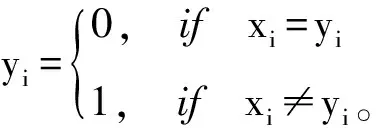
可见，不相关性指数r(X,Y)表示X和Y之间不相同基因的数目，r(X,Y)越大，X和Y之间的相关性越小。

3.1.2 相关性配对

在进行交叉操作之前，首先要将种群中的个体配对。简单遗传算法采用的方法是随机配对，可能导致无效的交叉操作出现。针对上述情况，本文在配对时按照不相关性指数进行配对，设初始种群中有N个个体，首先随机选取一个个体Xi，其余的N-1个个体构成群称为Xi的配对池位，设为{Y1，Y2,…，YN-1},分别计算Xi与Y1,Y2,…，YN-1的不相关性指数r(Xi,Yj)，j=1,2,…,N-1，选取最大的不相关指数r(Xi,Yj)对应的个体Yj作为Xi的配对个体；然后重复上述操作，直至所有个体配对为止。

3.2 有效区域—多点交叉

对于多个参数进行二进制编码时，染色体会携带多个参数的信息，文献[10]提出了—多点交叉的概念，即在染色体所携带的每个信息段同时执行一点交叉操作，具体数学描述如下：

假设2个参数x、y,其对应的二进制编码染色体包含2个参数的信息，2个参数的信息以“︱”分界表示，设有2个染色体：

X1：01001︱11011 (x1=01001，y1=11011)

X2：10001︱00100 (x2=10001，y2=00100)

由于每个染色体中包含有2个参数的信息，故每个信息段都采用一点交叉。在进行一点交叉时，首先要确定交叉点的有效区域，然后在该区域内随机选择交叉点，确保交叉操作能产生新的不同于父代的个体。交叉点的有效区域确定如下[11]：

Jmin=min{m|kim≠kjm,m=1,2,…,N}，Jmax=max{m|kim≠kjm,m=1,2,…,N}，N为最大基因座位数。

则交叉点的有效区域为[Jmin,Jmax]。对于上述染色体，2个参数交叉的有效区域分别为[1,2]和[1,5]。设2个参数的交叉点分别为2和4，则新产生的个体为：

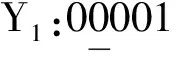
可见，经过这样交叉操作得到的子代完全不同于父代，是有效的交叉操作。

3.3 父子竞争产生新种群

简单遗传算法中用子代代替父代成为新种群，若经过交叉、变异操作后产生的子代均劣于父代，就会出现丢失父代最优个体的现象。为了确保子代总是优于或等于它们的父代，本算法引入了父子竞争机制，即由父代种群(N个个体)经过选择、交叉、变异产生子代种群(N个个体)，然后父代个体与子代个体共同组成待选种群(2N个个体)，选择适应度最大的前N个个体组成新种群，继续进行遗传操作，使得进化总是朝着最优方向进行，加快了收敛速度。

4 用改进的遗传算法与数值计算结合研究参数协同数学模型的建立

4.1 模型的建立

利用改进的遗传算法求解参数协同问题，关键是设计有效的评价函数，即适应度函数。本文构造的适应度函数如下

(5)

式中：fj为第j组热物性参数的适应度;Ti为目标温度场中第i点的值;TiC(j)为第j组热物性参数对应的温度场中第i点的值。

4.2 算法流程图

具体的算法流程见图4。

图4 用改进的遗传算法求解参数协同反问题流程图

5 算例

5.1 算例1

5.1.1 问题描述

设一建筑物的外墙由三层不同的建筑材料构成，如图1所示，墙体外侧的温度为T1=35 ℃，要求墙体内侧的温度控制在T4=20 ℃，各层墙体的相关计算参数见表1。现以目标温度场(如图5所示)为约束条件，探究各层建筑材料导热系数λ1、λ2、λ3的协同关系。

表1 三层墙体模型的计算参数

图5 三层墙体的温度分布

5.1.2 遗传设计

5.1.2.1 编码方式设计

本文采用二进制编码，由于有3个待求量，所以每个染色体均应包含3个参数信息，每个参数采用10位二进制码，每个染色体有30个基因位。

5.1.2.2 遗传算子设计

1)选择算子：本文采用轮盘赌法进行选择，每个染色体被选中的概率由其相对适应度来决定，即

(6)

式中：Pj为第j个染色体的相对适应度；fj为第j个染色体的适应度；N为种群大小，本文中N=100。

2)交叉算子：本文采用一多点交叉算子，交叉概率为0.9。

3)变异算子：本文采用多重均匀变异算子，变异概率为0.05。

5.1.2.3 评价函数及终止条件

评价函数为式(4)，要求个体适应度fj>1 000时终止，另一个终止条件为最大遗传代数终止，最大遗传代数取500。

5.1.3 计算结果

以图4所示的流程图为基础，应用大型编程软件FORTRAN编写计算机程序对问题进行数值计算。首先随机产生N=100个染色体作为初始种群，将每个染色体所包含的3个二进制编码串转化为参数实际值，代入离散后的控制方程求解该染色体对应的温度场。计算温度场时网格间距取Δx=1 mm。选择三层墙体中均匀分布的45个测点的温度值作为比较值，分别与目标温度场中对应点的值进行比较。满足图5所示温度场的λ1、λ2、λ3组合见表2。

表2 图5所示温度场的λ1、λ2、λ3匹配表

由计算结果可知，当墙体各层的厚度d1、d2、d3保持不变，各层墙体材料的导热系数λ1、λ2、λ3取表2中任一列的数值，都能使墙体内的温度分布与目标温度场一致，说明在以温度场为控制目标的条件下，各层材料的导热系数之间存在着一定的匹配关系。这一结果可以用来指导建筑节能设计，对于不同地区的建筑物，设计者可以根据本地区的实际情况，如本地区主要建筑材料的类型、市场价格、施工难易度等，选择合适的建筑材料进行组合，以达到相同的传热效果。本算例表明在一定的约束条件下，各层材料导热系数之间存在着协同关系。

5.2 算例2

5.2.1 问题描述

设一外墙为普通240 mm砖墙，导热系数为λ1=1.101 W/(m·k)，现需要做内保温，墙体外侧的温度为成都地区夏季室外干球温度T1=31.8 ℃，内侧温度为夏季空调室内设计温度T2=26 ℃，如图6所示。设定保温材料为挤塑聚苯乙烯板XPS，保温层厚度为50mm时砖墙内的温度场为目标温度场，如图7所示，现考查采用不同保温材料时，保温材料的导热系数和保温层厚度应为何值，才能够达到目标温度场？即以目标温度场为约束条件，探究保温层的导热系数和保温层厚度的协同关系。

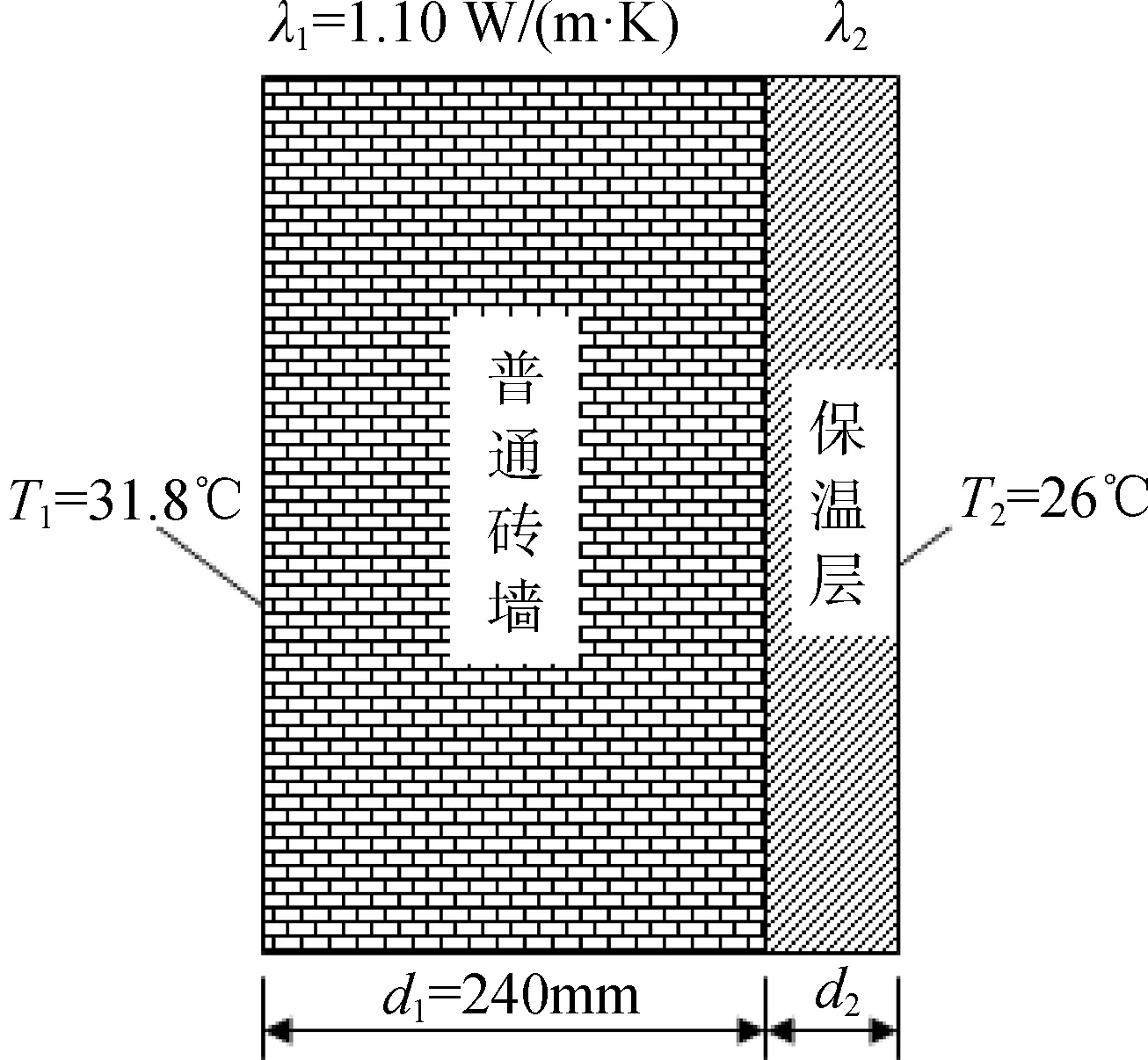
图6 墙体保温材料参数协同模型

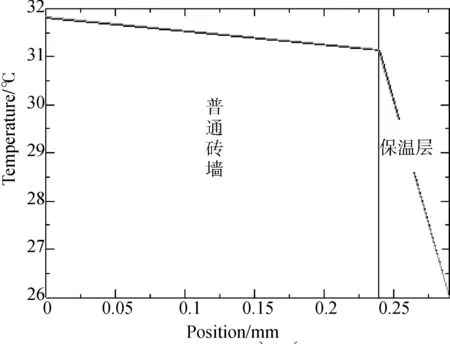
图7 图6墙体的温度分布

5.2.2 计算结果

经过数值计算,得到保温层导热系数和保温层厚度的协同关系如图8所示。

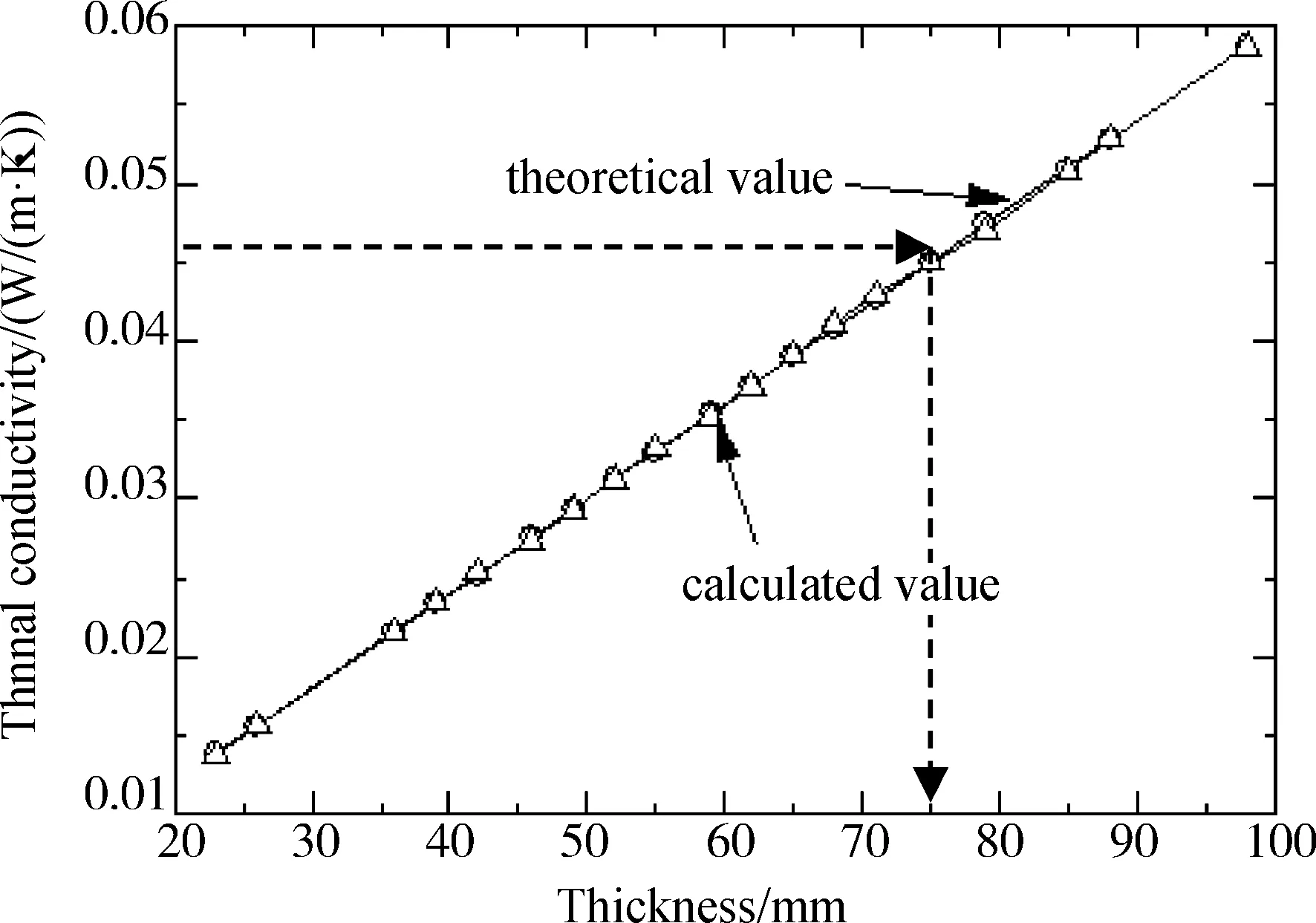
图8 保温层厚度与保温材料导热系数的协同关系

6 结论

1)本文首次提出了参数协同的概念，参数协同指的是在一定的约束条件下(如一定的温度场、热流密度或一定的能耗等)，各个参数之间的匹配关系。文中通过2个算例证明了在建筑物墙体稳态传热过程中，热工参数之间确实存在着一定的协同关系，对于建筑节能设计具有重要的指导意义。

2)本文将改进的遗传算法与导热反问题的数值计算相结合，首次将该方法应用于建筑物墙体参数之间的协同研究，数值计算结果表明, 此方法用来求解参数协同问题是行之有效的。

3)本文提出的计算模型不仅可以用于稳态传热多参数协同的研究，也可以用于非稳态传热多参数协同的研究。与传统的理论方法相比，本模型能够快速计算得到热工参数的精确值，为建筑节能设计中类似的反问题研究指出了一条可行之路。

[1]高宏逵.夏热冬冷地区办公建筑节能设计对策研究[D].哈尔滨：哈尔滨工业大学, 2007.

[2]徐春桃. 居住建筑外围护结构对室内热环境与建筑能耗的影响[D].重庆：重庆大学, 2008.

[3]Meral Ozel.Thermal Performance and Optimum Insulation Thickness of Building Walls with Different Structure Materials[J]. Applied Thermal Engineering, 2011(31) : 3854-3863.

[4]Yu Jinghua , Yang Changzhi , Tian Liwei , et al. A Study on Optimum Insulation Thicknesses of External Walls in Hot Summer and Cold Winter Zone of China [J]. Applied Energy, 2009(86) : 2520-2529.

[5]Beck J V,Blackwell B,Clair C R St.Inverse Heat Conduction-Ⅲ Posed Problem[M]. NewYork:Wilay,1985:1-40.

[6]Huang C H,Ozsik M N,Sawaf B.Conjugate Gradient Method for Determining Unknown Contact Conductance during Metal Casting[J]. Int J heat Mass Transfer, 1991,34(7)：1779-1785.

[7]智会强,牛坤,王秀春.基于遗传算法的热物性参数辨识[J]. 兰州理工大学学报,2006,32(1)：130-133.

[8]过增元.场协同原理与强化传热新技术[M].北京：中国电力出版社,2004.

[9]蔡良伟,李霞.遗传算法交叉操作的改进[J]. 系统工程与电子技术,2006，28(6)：925-928.

[10]关旭,张春梅,王尚锦.一种改进的自适应遗传算法[J]. 微机发展,2003，13(11)：41-44.

[11]任世军,陈亮.遗传算法中交叉操作的改进策略[J]. 哈尔滨商业大学学报,2006，22(5)：60-62.