市场分割、汇率期限结构与外汇市场变动的非对称性*
李仲飞, 邓柏峻, 张 浩
一、引 言
2009年4月,中国开展跨境贸易人民币结算试点,人民币国际化迈出了坚实的一步。从其他国家经验来看,国际货币的形成离不开离岸金融市场的推动作用。美元的国际化得益于欧洲美元市场的建立,而日元的国际化则有赖于东京离岸金融市场的设立。自从跨境贸易人民币结算试点以来,香港的人民币离岸市场发展迅速、离岸市场人民币的规模不断增加。离岸市场的不断发展壮大以及我国资本跨境自由流动的受限,使得人民币市场逐渐形成境内和境外两个市场,汇率等相关产品也存在两个价格,即存在市场分割的现象。其中,即期市场包括在岸人民币汇率(CNY-SPOT)和离岸人民币汇率(CNH-SPOT);远期市场则包括在岸人民币汇率远期(CNY-DF)、离岸人民币汇率远期(CNH-DF)和无本金交割人民币远期(NDF)。然而,在岸市场和离岸市场的汇率形成机制却存在差异:前者是基于经常账户国际收支的情况,并以国内经济发展为基础、实行以市场供求为基础的有管理浮动汇率制度;而后者则是基于离岸市场人民币的需求和供给方的供求关系。汇率形成机制的差异使得离岸市场汇率更具有“市场色彩”,其波动程度也会相应较大(见图1);而在岸市场汇率更具有“政策色彩”,其变化较为缓和。从图1可以看出,尽管CNY和CNH市场的走势较为一致,但也会存在偏离。而这种离岸市场与在岸市场人民币兑美元汇率的偏离会使得相关经济主体(进口商或者出口商)获利。

图1 人民币兑美元在岸市场(CNY)与离岸市场(CNH)汇率
市场分割引起的在岸与离岸两个市场的人民币价格差异,使得相关的衍生品价格也存在差异,并且这种差异会随着远期汇率期限结构的不同而不同。在人民币国际化不断推进的背景下,随着资本管制的逐步放松,在岸与离岸两个市场的联系越来越紧密,在岸与离岸市场的价格应趋于一致,从而避免人民币市场分裂、增加人民币市场的统一和透明度、提高人民币的国际地位。而且,从韩国和台湾的经验来看,在岸与离岸两个市场价格的统一有助于减少套利、降低汇率市场波动、维护汇率稳定。若两个市场价格差异较大或变动不一致,资本项目下可自由兑换的开放必然会引起大量套利资本进入境内市场,对我国的金融市场带来严重冲击。因此,本文将主要研究具有不同期限结构的离岸和在岸市场人民币汇率受到冲击时的变动特征,分析不同期限结构下受到外部冲击时两个市场的相关程度,从而为进一步研究资本项目下可自由兑换的可行性奠定基础。
2005年汇率形成机制改革以来,国内学者将在岸市场和离岸市场的研究集中于NDF市场对在岸市场汇率的先导作用上。代幼渝和杨莹(2007)使用格兰杰因果关系检验的方法研究了离岸NDF市场、在岸外汇远期市场(CNY-DF)和在岸外汇即期市场(CNY-SPOT)的关系,发现在岸远期和即期汇率能够引导离岸NDF汇率。徐剑刚等(2007)使用MGARCH模型研究了NDF市场和CNY-SPOT市场的均值和波动溢出效应,结果发现NDF市场对CNY-SPOT市场有报酬溢出效应,境外因素已经开始影响在岸即期市场。此外,黄学军和吴冲锋(2006)、李晓峰和陈华(2008)、陈蓉等(2009)、陈波帆(2012)、贺晓博和张笑梅(2012)、伍戈和裴诚(2012)也都分别使用不同的方法和样本研究了NDF市场对CNY市场和CNH市场的影响。但是,以上文献基本上都是使用格兰杰因果关系检验或GARCH类模型,研究不同市场之间的线性相关关系,却忽视了不同市场之间的非线性关系。因此,本文使用Copula模型来研究不同市场之间的非线性关系。根据Sklar定理,任意多维随机变量的联合分布函数都可由各随机变量边缘分布的函数来表示,这个函数被称为Copula函数。其中,所有关于随机变量边缘分布的信息都包含在边缘分布函数中,所有关于随机变量相依结构的信息都包含在Copula函数中,因此,Copula模型可以很方便地将多维随机变量的边缘分布与相依结构分开研究。Copula模型在外汇市场中的应用可参见帕顿(Patton,2006)、龚朴和黄荣兵(2008)、蔡霞等(2009)的研究。而使用Copula函数研究人民币在岸与离岸市场的相关文献目前并不多见。张自然和丁日佳(2012)使用Copula函数研究了CNY-SPOT市场、3月期CNY-DF市场和3月期NDF市场的相关关系,发现上述市场间的汇率变动存在“不对称效应”:即面临不同冲击时,各市场汇率变动的同步性也不一样。不同于张自然和丁日佳(2012)的研究,本文认为:在研究汇率变动的“不对称效应”时,应该将相同类型的市场进行比较,即研究在岸与离岸市场的即期汇率之间、在岸与离岸市场的相同期限远期汇率之间的关系,这主要是因为即期市场与远期市场的汇率形成机制和影响因素均不相同,相同期限市场之间的比较会更有意义。同时,对不同期限的远期汇率市场进行比较有助于更好地探讨远期汇率受到冲击时期限结构对汇率变动的影响。
本文将采用Copula-GARCH-skewT模型对CNY-SPOT市场和CNH-SPOT市场以及1月、3月、6月、9月和12月期等不同期限的CNY-DF市场和NDF市场间汇率受到冲击时的表现进行研究,通过常参数和时变参数的SJC-Copula函数的估计结果来比较相同类型市场间受到升(贬)值冲击时的反应,以及不同期限结构汇率产品间的差异,从而为进一步研究资本项目下可自由兑换的可行性和外汇率管理提供依据。
二、Copula-GARCH模型的构建
构建Copula-GARCH-skewT模型分为两步,先要确定边缘分布,然后再确定所选用的Copula函数用来描述不同边缘分布的相依结构。具体而言,在拟合边缘分布以后,要根据相应的边缘分布对汇率收益率序列进行概率积分变换,并选择合适的Copula模型连接概率积分变换后的序列。因此,Copula-GARCH-skewT模型不仅可以描述不同边缘分布所具有的自相关和异方差特征,还能灵活地选择不同的Copula函数刻画序列之间不同的相依关系。本文所使用的Copula-GARCH-skewT模型构建如下。
(一)边缘分布拟合
由于金融时间序列通常具有自相关和波动集群的特点,因此本文使用AR(p)-GARCH模型对汇率收益序列进行拟合,其中p表示自相关阶数。与Patton(2004)相同,本文使用skew-T分布来拟合GARCH模型的标准化残差序列*这是因为skew-T 分布能够更好地描述汇率收益序列尖峰厚尾和偏斜的特征。。因此,本文最终使用AR(p)-GARCH(1,1)-skewT模型作为边缘分布模型。AR(1)-GARCH(1,1)-skewT模型的表达式如下:
Ri,t=c0+c1Ri,t-1+ei,t
(1)
(2)
(3)
其中,Ri,t是汇率的收益率,ei,t是残差项,hi,t代表条件方差,εi,t服从skew-T分布,υ代表skew-T分布的自由度,λ代表skew-T分布的偏斜程度。
(二)Copula模型的构建
常见的Copula函数主要有多元正态Copula函数,多元t-Copula函数,阿基米德类Copula以及极值Copula函数等*多元正态Copula函数和多元t-Copula函数具有对称性,其尾部相关系数(见下文定义)也是对称的,因此这两种Copula函数不能刻画不同市场状况下汇率变动的不对称性。常见的阿基米德类Copula函数主要有Gumbel、Clayton和Frank-Copula,其中,Gumbel-Copula函数不能捕捉下尾相关性,Clayton-Copula函数不能捕捉上尾相关性,Frank-Copula函数不能捕捉上下尾相关性。而JC-Copula函数则能够同时刻画边缘分布的上尾、下尾相关关系,并且JC-Copula函数的参数与上下尾相关系数有一一对应的关系,从而可以根据这种对应关系来定义JC-Copula函数中参数的动态演变过程。但是JC-Copula函数的主要缺陷是该函数不能刻画边缘分布的对称关系,甚至当上尾、下尾相关系数相等时,对应的边缘分布也是不对称的。。本文采用Patton(2006)提出的对称JC-Copula (SJC-Copula),其函数形式如下:
(4)
(4)式中u和v是边缘分布的分布函数值,CJC(u,v)的表达式如下:
CJC(u,v)=1-{1-{[1-(1-u)k]-γ+[1-(1-v)k]-γ-1}-1/γ}1/k
(5)
其中κ和γ是模型中的参数,且与上尾、下尾相关系数有一一对应关系。
Copula函数的一大优点是它能刻画边缘分布之间的尾部相关性,即用来描述当极端情况(升值或贬值冲击)发生时,边缘分布序列的同步程度。如果两个汇率市场间的Copula函数为C(u,v),其中u,v分别为对汇率收益率序列进行概率积分变换后得到的序列,相应的下尾相关系数和上尾相关系数的定义分别为:
(6)
(7)
根据定义,下尾相关系数描述了汇率市场面临升值冲击时的同步程度,上尾相关系数描述了汇率市场面临贬值冲击时的相关程度。SJC-Copula函数能够同时描述上尾、下尾相关关系,并且当上尾相关系数与下尾相关系数相等时,表明对应的边缘分布在冲击下的变动是对称的,因此,SJC-Copula函数能够刻画分布变动的对称性与不对称性。Patton (2006)根据上尾、下尾相关关系的运行规律,描述了SJC-Copula函数的时变参数估计,参数的演化方程如下:
(8)
(9)
其中Λ(·)为Logistic函数,Λ(x)=(1+e-x)-1,以保证τU和τL在(0,1)之间。
(三)Copula-GARCH模型的估计方法
Copula-GARCH非常适合使用两步极大似然估计方法,即先用极大似然估计法估计边缘分布的参数,再对Copula函数进行极大似然估计。估计方法如(10)—(13)式:
f(x1t,x2t;θ1,θ2,θct)=f1(x1t;θ1)·f2(x2t;θ2)·c(F1(x1t;θ1),F2(x2t;θ2);θct)
(10)
其中,f1和f2代表边缘分布的概率密度函数,θ1和θ2代表边缘分布的参数,c(u,v)代表Copula函数的概率密度函数,θct是Copula函数的参数。
第一步,用极大似然法分别估计出边缘分布的未知参数θ1和θ2:
(11)
(12)
第二步,用极大似然估计法估计Copula中的未知参数θct:
(13)
根据(1)—(13)式,本文将使用Copula-GARCH-skewT模型,研究离岸市场与在岸市场人民币汇率受到冲击时的动态关系。
三、实证分析
(一)数据来源和统计性描述
本文选取在岸和离岸市场的即期和远期汇率收益率序列分别进行对比*汇率的收益率序列Rt由汇率序列(直接标价法)取对数后再取差分最后乘以100而得,计算公式如下:Rt=100×(lnEt-lnEt-1),本文使用这种处理方式主要是因为原始汇率序列的非平稳性。。对于即期汇率数据,本文选择了2011年6月28日至2013年3月22日的CNY即期日汇率收盘价和CNH即期日汇率定盘价进行对比*数据起点选择2011年6月28日是因为2011年6月27日之前的CNH即期数据为交易价,之后的为定盘价。为了避免统计口径不一致产生的偏误,并尽量利用最新的数据集以反映最新的汇率信息,本文选择2011年6月27日之后的CNH即期汇率数据。,将原始数据转化为收益率序列并保留两个市场都有交易日的日收益率数据后,一共获得410对观测值。对于远期汇率数据,本文选择了2009年11月3日至2013年3月22日的CNY-DF与NDF市场日汇率数据。具体而言,本文选择了CNY-DF的12月期(用CNY-12M代替,下同)、9月期、6月期、3月期和1月期产品与NDF的对应产品进行对比*本文不选择CNH-DF作为离岸市场远期汇率是因为彭博数据库中CNH-DF汇率的时间长度太短,从而影响实证结果的可信度。。同样将汇率数据转化为日收益率序列,并保留对应市场都有交易日的序列后,本文获得12月期产品793对观测值,9月期产品788对观测值,6月期产品787对观测值,3月期产品794对观测值,1月期产品791对观测值。各组数据的描述性统计如表1所示。
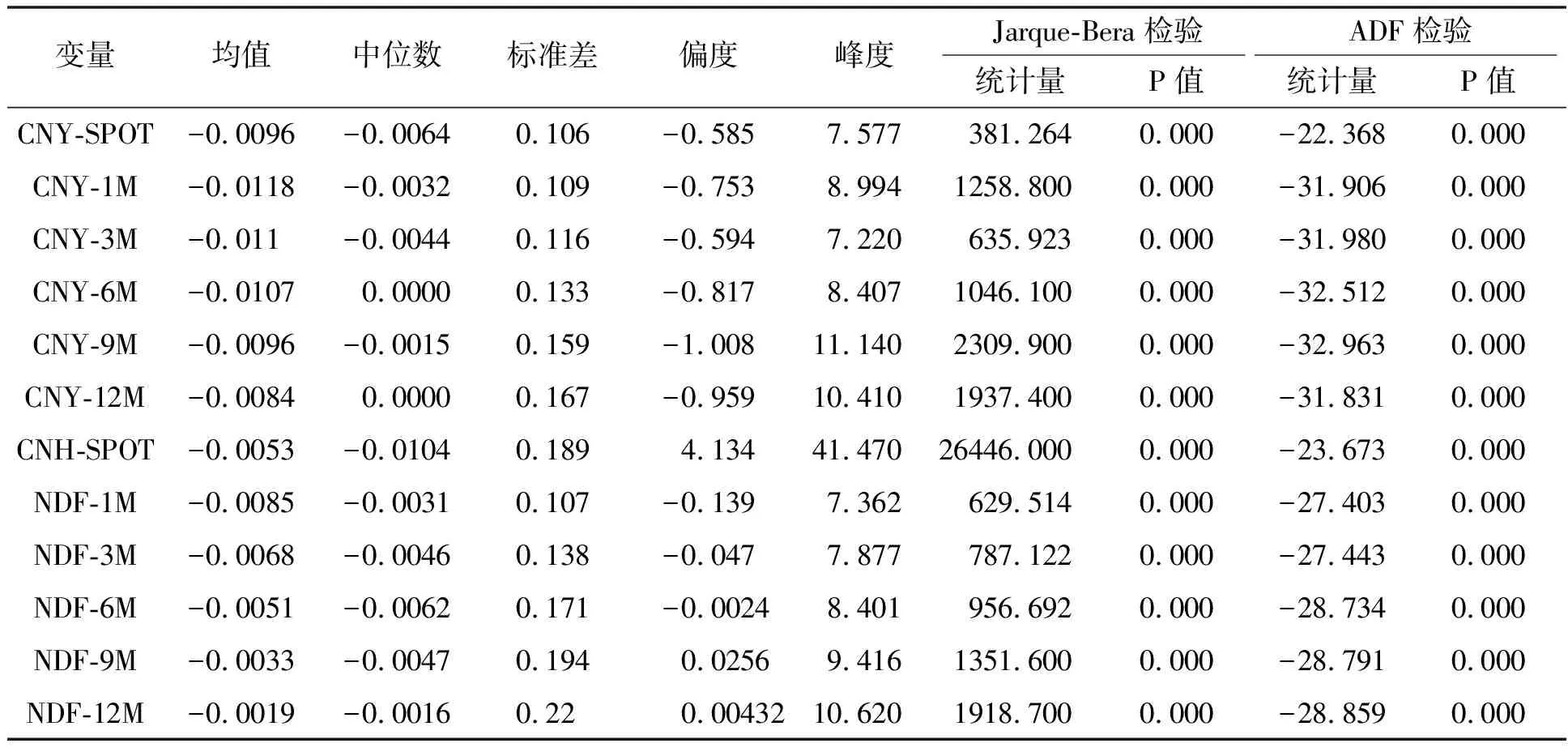
表1 相关数据的描述性统计结果与平稳性检验
从表1的结果看,所有市场汇率收益率的均值为负数,说明在样本期内人民币基本保持升值趋势,而且在岸市场的收益率和标准差普遍低于相对应的离岸市场,说明在岸市场人民币的单边升值趋势更加明显,且波动程度较低,市场稳定性更强。此外,通过离岸市场和在岸市场中不同期限的人民币远期产品比较可知,长期限产品的平均升值幅度要小于短期限产品,而标准差则明显大于短期限产品。这可能是因为就长期而言,人民币升值的预期并不十分明显,且受到的外部影响较大,因此波动程度较高。用ADF检验方法对收益率序列进行单位根检验,结果表明所有收益率序列均拒绝单位根的原假设,从而所有收益率序列都是平稳的,可以使用AR-GARCH模型进行建模。由于本文使用AR(p)-GARCH(1,1)-skewT*表1中偏度和峰度反映收益率序列具有尖峰和有偏的特征。JB统计量值和对应的P值说明所有收益率序列均拒绝了正态分布的原假设,因而本文使用偏态T分布。对收益率序列进行建模,因此,先对收益率序列进行自相关的Ljung-Box-PierceQ检验和ARCH效应检验,以确定合适的滞后阶数,检验结果见表2。从Ljung-Box-PierceQ检验和ARCH效应检验可以看出,在5%的显著性水平下,所有的汇率收益率序列都有不同程度的自相关和条件异方差,其中CNY-SPOT、CNH-SPOT、CNY-DF的汇率收益率序列存在1阶或1阶以上的自相关,而NDF的汇率收益率序列存在2阶或2阶以上的自相关;并且所有的汇率收益率序列均存在显著的异方差效应。
(二)边缘分布模型的估计结果
根据表1和表2的结果,并经过反复比较,本文选取AR(1)-GARCH(1,1)-skewT模型拟合CNY-SPOT、CNH-SPOT以及CNY-DF市场的汇率收益率序列,选择AR(2)-GARCH(1,1)-skewT模型拟合NDF市场的汇率收益率序列,相关的模型参数估计如表3所示。其中,CNY-DF市场的AR1系数在5%的显著性水平上均显著不为零;NDF市场的AR2系数在5%的显著性水平上均显著不为零,与表2中的Ljung-Box-Pierce Q检验结果相符;所有市场中的β系数在5%的显著性水平上均显著不为零,表明存在一定的条件异方差效应,与表2中的ARCH效应检验结果相符。CNY-6M、CNY-9M、CNY-12M和CNH-SPOT市场的λ值在5%的显著性水平上均显著不为零,说明收益率数据的分布存在偏斜,而skew-T分布很好地描述了汇率收益率分布的这种偏斜效应,从而表明使用skew-T分布对边缘分布模型进行拟合的合理性。
边际分布拟合效果的优劣直接决定Copula模型的估计效果。如果边缘分布误设,那么对标准化后的残差序列进行概率积分变换将不服从[0-1]均匀分布,这将导致Copula模型参数估计发生偏误,从而得出错误的结论。因此,对边缘分布的拟合效果进行检验是非常必要的。一般而言,可以从两个方面评价边际分布的拟合效果,一是检验标准化后的残差是否排除了自相关性,本文使用Ljung-Box-PierceQ检验方法对标准化后的残差进行检验,发现所有序列均不存在自相关性*限于篇幅,本文不再列出,如有需要,请与作者联系。;二是对标准化残差序列进行概率积分变换,并对变换后的新序列进行[0,1]均匀分布的Kolmogorov-Smirnov(K-S)检验,以检验新序列是否具有同[0,1]均匀分布。K-S检验的结果如表4所示。表4中的P值表明,所有市场的汇率收益率序列进行概率积分变换后均服从[0,1]均匀分布。
以上的自相关检验和K-S检验表明,通过AR(p)-GARCH(1,1)-skewT模型拟合后的汇率收益率序列,再经过概率积分变换以后服从独立[0,1]均匀分布,满足下一步使用Copula模型进行建模的条件。并且,以上结果说明本文使用AR(p)-GARCH(1,1)-skewT模型对边缘分布进行拟合是合理的,且拟合效果较好。

表4 边缘分布的K-S检验
(三)Copula模型的拟合结果分析
在边缘分布估计结果的基础上,本文使用极大似然估计法对时变参数以及常参数的SJC-Copula模型进行估计。本文将6个在岸市场汇率分别与对应的离岸市场汇率进行两两对比,一共得到12个Copula函数估计结果(包括6个时变参数SJC-Copula和6个常参数SJC-Copula),估计结果如表5所示。

表5 SJC-Copula 参数拟合结果
从即期市场常参数SJC-Copula模型的实证结果来看,样本期内CNY和CNH两个市场的上尾相关系数和下尾相关系数分别为0.1889和0.1887,两个数值显著异于0且基本相等,这说明两个市场呈现出一定的同步性,且面临人民币的升值或者贬值冲击时,两个市场的同步程度基本上是对称的。这可能是因为,人民币作为主权货币,其价格变动无法脱离基本的名义锚的制约。在宏观经济发展趋势没有重大改变的情况下,无论是按照购买力平价或利率平价,或是其他汇率决定理论,汇率本身都不会出现过度的波动。而在境内外两个市场上,由于人民币核心价值的一致性,即便汇率形成机制略有不同,均并不会改变其本身的价值,因此在平均水平上,两者的变动是一致的。
然而具体到不同的时点,两个市场的对称性却呈现出明显的差异。从图2可以发现,下尾相关系数在2011年底经历了大的波动后,从2012年3月开始基本上在0附近;而上尾相关系数尽管有所波动,但一直保持在较高的数值,两个市场体现出一定的非对称性。这主要是因为,这一时期,我国经济已经基本摆脱2008年次贷危机的影响,各项经济指标开始逐步回升;同时受欧债危机的波及和影响,大量投资于欧洲的资本开始撤出,并流入中国,热钱的纷纷流入造成了我国经常项目和资本项目的双顺差,同时也从根本上促使人民币不断升值。在岸市场由于受到经济基本面的影响,人民币步入升值轨道,在岸市场汇率的变化基本符合我国汇率市场化进程的要求*相对而言,我国政府更注重汇率的稳定程度,即便是在人民币的升值阶段,小幅长期的升值路径也是首选。。而在离岸市场,人民币的升值则体现离岸市场对于人民币的需求,由于香港市场人民币存款和投资产品具有较高的收益率,加之跨境人民币结算业务的开展加大了人民币的需求,从而使得人民币在离岸市场上也长期处于上升通道。
但是,由于人民币资金体量以及汇率形成机制的差异,当面临人民币升值冲击的时候,两个市场会体现出巨大的差异性:在离岸市场,由于人民币资金池体量较小,汇率受到市场供求双方的影响较大,因此对于冲击的反应会更加灵敏,当出现人民币升值冲击时,相应的升值幅度也较大;而在岸市场汇率尚未完全市场化,加之人民币存量资产体量较大,相同的冲击并不会带来过度的反应,同时为了确保人民币汇率在合理、均衡的水平上保持稳定,央行并不会在原有升值的趋势中提高人民币汇率波动幅度。因此,在面对人民币升值冲击时,两个市场会产生一定差异,所以具有较低的相关性。当面临人民币贬值冲击时,离岸市场会根据市场变化做出反应,而在岸市场对于升值通道中的贬值也具有一定的容忍度,从而两个市场在面对贬值冲击时具有一定的同步性。

图2 在岸市场与离岸市场即期汇率上下尾时变相关系数

图3 在岸市场与离岸市场汇率差额图*文中的汇率差额图均是采用离岸市场减去对应在岸市场的汇率所得的差额,这里为了便于比较,所有的数值都是在原始数据上扩大了10000倍。由于使用的是间接标价法,差额大于零表示离岸市场人民币的价值相对较低。
进一步通过离岸、在岸市场的即期差额图(图3)可以看出,在2011年8月—2011年12月,CNH市场汇率均高于CNY市场,即在岸市场的人民币价值较高。而在样本期内的其他时间段,两个市场的差异较小。对比下尾相关系数和差额图可知:当CNH市场的汇率高于CNY市场时,由于离岸市场人民币汇率和在岸市场存在差异,面临人民币升值的冲击时,两个市场的同步性会突然提高。这主要是因为,当人民币在离岸市场的价值由于某种原因相对较低时,人民币的升值冲击会使得离岸市场迅速回归到升值通道中来;而在岸市场由于其本身处在升值通道中,两者的一致性突然提高,因此下尾相关系数会突然放大。但当两个市场汇率差距比较小,即两个市场汇率本身较为一致时,面对升值冲击时,由于在岸市场反应较为“迟缓”,因此两者的下尾相关系数较小,即两个市场的同步性较差。

图4 1月期的在岸市场远期产品与NDF的对应产品上下尾时变相关系数

图5 3月期的在岸市场远期产品与NDF的对应产品上下尾时变相关系数
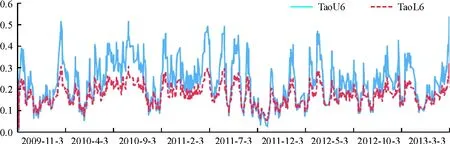
图6 6月期的在岸市场远期产品与NDF的对应产品上下尾时变相关系数
从表5中的常参数Copula函数拟合结果来看,远期市场的上下尾相关系数基本都高于即期汇率市场,这表明相对即期汇率市场而言,远期市场汇率在面临冲击时的同步性要更强。这主要是因为远期市场受到的冲击更多的是由预期产生的,在相同的经济背景下,预期对在岸市场和离岸市场的效果应该是基本一致的,因此在远期市场,无论是升值还是贬值,冲击对两个市场的影响都相对更一致。
其中1月期和3月期的远期市场实证结果表明,远期汇率受到贬值冲击后的反应较受到升值冲击后的反应同步性更高。这说明对于短期外汇远期产品*本文中所指的短期主要是1月期和3月期产品,以此区分于9月期和12月期的长期产品,同时本文将6月期产品称为中期产品。而言,市场依然认为人民币相对处于升值通道内,若冲击造成趋势性的改变(由升值转变为贬值),则两个市场的同步性会相对较高。从1月期和3月期的远期市场时变相关系数(见图4和图5)可以发现,两个市场的下尾相关系数都较为稳定,尤其是1月期远期市场的下尾相关系数在2012年后的变化基本与即期市场一致;而上尾相关系数则在0.3附近有较大的波动。这也充分表明一旦遇到贬值冲击,在岸和离岸两个市场都会做出一定的反应,两个市场的联动性会更加明显。由此可见,对于短期的外汇远期产品,其面临外部冲击时会产生一定的非对称性,且这种非对称性会表现为“面临贬值冲击时的同步性高于面对升值冲击时的同步性”。而对于6月期的外汇远期市场,当受到不同类型的冲击时,两个市场的同步程度基本是对称的(见图6)。

图7 9月期的在岸市场远期产品与NDF的对应产品上下尾时变相关系数
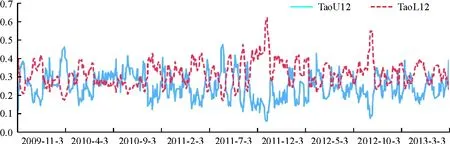
图8 12月期的在岸市场远期产品与NDF的对应产品上下尾时变相关系数
而对于9月期和12月期的外汇远期市场,表5和图7、图8的结果表明,长期外汇远期产品的上尾相关系数相对于短期外汇远期产品会减小,而下尾相关系数会明显增加;同时,远期汇率受到冲击后的反应会发生反转,上尾相关系数会小于下尾相关系数,远期汇率受到升值冲击后的反应较受到贬值冲击后的反应的同步性提高,此时,长期外汇远期产品面临外部冲击时产生的非对称性会表现为“面对升值冲击时的同步性高于面对贬值冲击时的同步性”。这可能是因为对于长期外汇远期产品,市场的不确定因素增加,远期汇率产品价格厘定难度增加,变动的幅度也相对加大。而且从9月期和12月期的外汇远期市场汇率差额图也可以看出,离岸市场对于人民币升值的预期更加强烈。鉴于NDF市场对于在岸远期市场具有一定的先导作用,因此,一旦市场受到人民币升值的冲击,两个市场都会做出反应,从而同步性增强。
四、结 论
本文采用Copula-GARCH-skewT模型对CNY-SPOT市场和CNH-SPOT市场、不同期限的CNY-DF市场和NDF市场之间的关系进行研究,并探讨了受到升值(或贬值)冲击时,各市场的反应。研究发现:由于人民币外汇市场存在分割现象,人民币汇率出现了两个市场、两种价格,而汇率形成机制的差异使得分割市场中的产品面对相同的冲击时会产生不一样的反应。具体表现在:首先,样本期内人民币基本保持升值趋势,且在岸市场人民币的单边升值趋势更明显、波动程度更低,市场稳定性更强。同时,无论是离岸市场还是在岸市场,长期而言,人民币升值的预期并不十分明显,且受到外部的影响较大,因此波动程度较高。其次,常参数的SJC-Copula结果表明,当即期市场面临人民币的升值或者贬值冲击时,两个市场的变动程度是对称的。但时变参数SJC-Copula结果表明,具体到不同的时点,两个市场面临不同类型冲击时的同步性则体现出明显的差异,当面对人民币升值冲击时,两个市场具有较低的同步性;而当面临人民币贬值冲击时,两个市场具有较高的同步性。这主要是因为两个市场的汇率形成机制存在差异。再次,相对即期汇率市场而言,远期汇率市场的常参数尾部相关系数较大,说明远期汇率市场的同步性高于即期市场。对于短期外汇远期产品,其面临外部冲击时会产生一定的非对称性,且这种非对称性会表现为“面临贬值冲击时的同步性高于面对升值冲击时的同步性”。而长期外汇远期产品面临外部冲击时产生的非对称性会表现为“面临升值冲击时的同步性高于面对贬值冲击时的同步性”。最后,从结果来看,在岸和离岸市场各自的“政策色彩”和“市场色彩”浓厚,尤其是短期内面对升值冲击时,“政策市”和“市场市”间还存在一定的差异,若此时资本账户过快开放必会造成资金在两个市场间逐利从而给经济体系带来冲击。只有资本账户采取渐进、小步的开放,那么随着跨境资金流动的频繁,在岸市场的“市场性”逐渐增强,最终才会实现两个市场的趋同。
[参 考 文 献]
蔡霞,贺广婷,关静,李秀敏.基于外汇汇率相关结构的多变点分析. 系统工程理论与实践, 2009,(3).
陈波帆.香港离岸人民币市场与在岸人民币市场互动关系研究. 新金融, 2012,(2).
陈蓉,郑振龙,龚继海.中国应开放人民币NDF市场吗?——基于人民币和韩圆的对比研究. 国际金融研究, 2009,(6).
代幼渝,杨莹.人民币境外NDF汇率、境内远期汇率与即期汇率的关系的实证研究. 国际金融研究, 2007,(10).
龚朴,黄荣兵.外汇资产的时变相关性分析. 系统工程理论与实践, 2008,(8).
贺晓博,张笑梅.境内外人民币外汇市场价格引导关系的实证研究——基于香港、境内和NDF市场的数据. 国际金融研究, 2012,(6).
黄学军,吴冲锋.离岸人民币非交割远期与境内即期汇率价格的互动:改革前后. 金融研究,2006,(11).
李晓峰,陈华.人民币即期汇率市场与境外衍生市场之间的信息流动关系研究. 金融研究, 2008,(5).
伍戈,裴诚.境内外人民币汇率价格关系的定量研究. 金融研究, 2012,(9).
徐剑刚,李治国,张晓蓉.人民币NDF与即期汇率的动态关联性研究. 财经研究, 2007,(9).
张自然,丁日佳.人民币外汇市场间不对称汇率变动的实证研究. 国际金融研究, 2012,(2).
Patton, A.J. 2004.On the out-of-sample importance of skewness and asymmetric dependence for asset allocation.Journal of Financial Econometrics, 2,(1): 130—168.
Patton, A.J. 2006.ModelingAsymmetric Exchange Rate Dependence.International economic review,47,(2):527—556.

