厦门湖滨西路口跨线桥静动载试验研究
刘羽宇
(中国民用航空飞行学院飞行技术学院,四川广汉618307)
随着我国钢铁工业和钢结构技术的发展,钢结构桥梁越来越被众多建设单位采用,钢箱连续梁桥更是以其断面小、抗扭刚度大、强度高、重量轻、外形简洁流畅、设计方便和施工快捷迅速等优点[1]而在城市交通中被广泛应用。
已建成的湖滨西路口跨线桥位于厦门市快速交通系统(BRT)一期工程一号线岛内段湖滨西路口处。主梁为4跨(27.5 m+2×42.5 m+27.5 m)连续钢箱梁,钢箱梁采用单箱单室斜腹板截面,梁高2.60 m。箱梁顶宽9.80 m,箱底宽4.46 m,两侧悬臂长度为1.78 m。为检验该桥的设计合理性与施工质量,确定工程的可靠性,判断其实际承载能力,评价其在设计使用荷载下的工作性能,对该桥进行了自振特性及静、动载试验研究,并用有限元软件做了对比计算分析。
1 试验加载设计与试验方法
1.1 试验加载设计
为合理进行此连续钢箱梁桥的荷载试验,针对该桥做了相应的详细计算分析工作。本次试验采用桥梁博士软件计算了该钢箱梁桥在城-B、BRT荷载以及直线电机B型车活载(设计控制荷载)作用下的结构弯矩包络图,据此并结合桥跨实际情况确定了本桥的试验工况。全桥选取3个试验断面,分别为第3跨及第4跨跨中最不利正弯矩及支点附近最不利负弯矩工况,如图1所示。分别在每跨的1/4、1/2、3/4跨截面处设2个挠度测点,分别在A-A、B-B、C-C截面设17个应变测点,动应变测点选择第三跨跨中C-C及第四跨跨中A-A截面上各三个应变测点进行,如图2,图中“圆圈+箭头”为挠度测点,实心三角形为静应变测点,带实心圆点三角为动应变测点。

图1 测试断面(单位:mm)

图2 主梁测点布置(单位:mm)
1.2 试验内容与方法
桥梁荷载试验是一项复杂而细致的工作,技术含量高,涉及面广,一般分为静载与动载试验[2]。
1.2.1 静载试验内容与方法
静载试验,包括各试验断面的应力测试和加载跨L/4、L/2、3L/4位置的竖向挠度,经过优化合并后,所确定的加载工况以及相应的检验、观测项目见表1,每辆试验车辆重380±10 kN,轴距3.85 m+1.40 m。正式试验前,先对结构预加载2次,以消除桥梁的非弹性变形。每个工况加载2次,加载时间应充分长以保证桥梁完全变形,卸载以后,同样需等结构充分回复到初始状态后再进行加载。
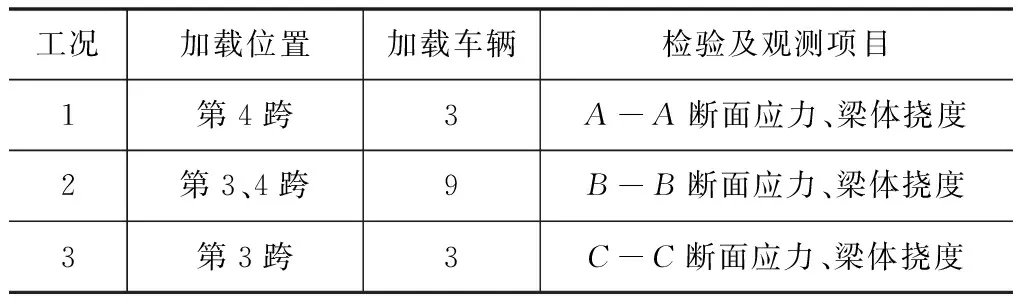
表1 各静力加载工况及观测项目
1.2.2 动载试验内容与方法
动力测试主要包括自振特性测试和行车激振试验。
自振特性测试,是研究振动问题的基础[3],主要测定桥梁的自振频率、振型和阻尼比。采用脉动法测试该桥梁的自振频率,并采用模态分析法得到对应频率的振型,根据功率谱用半功率点带宽法计算阻尼比。试验中,所记录的信号要足够长,不饱和信号需要补充测试。
动载试验分为无障碍行车试验、跳车试验和制动试验,用一辆载重汽车作为加载荷载。受现场条件限制,无障碍行车试验车速为10~30 km/h,跳车试验行车车速5~30 km/h,制动试验行车车速30 km/h。
2 有限元模型及计算方法
采用ANSYS有限元软件建立该钢箱梁桥的计算模型,如图3。模型采用直接生成方法建立,其优点是可以对几何形状及每个节点和单元的编号有完全的控制。根据桥梁主体是由钢板这种薄壁件焊接而成且分析过程处于弹性阶段的特点,选用壳单元shell63对其进行离散, 这种单元可以承受平面内荷载和法向荷载,能够模拟计算实际结构的弯曲和
薄膜应力。为了在保证计算结果可靠性的基础上降低运算规模,有限元网格在加载附近和测点附近划分较细,其它部分较粗[4]。桥梁上的附属设施(包括桥面铺装),由于对桥梁的刚度贡献较小,故仅将其质量折算到桥梁中,而不单独模拟[5]。
计算内容主要包括桥梁的自振特性和静载工况(与静载试验相对应)的计算。自振特性采用分块Lanczos法求解器计算,具有求解精度高、速度快的特点。静载工况计算由于主要研究桥梁各测试截面的挠度及应变,因此,可将加载车辆简化为集中力荷载来计算, 集中力的大小及施加的位置根据试验车辆的质量和轮位确定。
图3 桥梁模型局部
3 试验结果与分析
3.1 静载试验结果与分析
3.1.1 挠度结果与分析
各工况下梁体挠度实测和计算值见表2。可以看出,实测值和计算值较接近,第3跨梁体最大位移实测值为14.97 mm,计算值为18.50 mm,第4跨梁体最大位移实测值为5.13 mm,计算值为7.11 mm,桥跨结构具有足够的刚度。各工况下挠度结构校验系数介于0.60~1.05之间,基本处于合理范围内。

表2 梁体静挠度实测值与计算值比较 mm
3.1.2 应力实测结果与分析
各工况下该桥测试截面应力实测和计算值见表3。可以看出,实测值和计算值同样较为接近,测试截面的应力结构校验系数介于0.76~0.95之间,处于合理范围内。各工况中,梁体应变回零良好, 结构处于弹性受力状态。该桥测试截面应力较小,结构具有足够的强度。
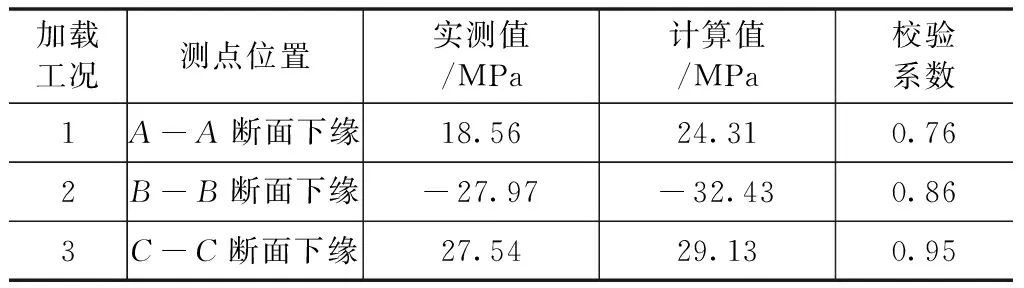
表3 梁体应力实测值与计算值比较
3.2 动力试验结果与分析
3.2.1 自振特性结果与分析
由于结构振动是由若干个对应不同频率的主振动迭加而成,而相应于基频的主振动在结构的合成振动中占很大比例,是结构振动的主要部分。因而,通常主要以结构第一阶主振动来评价结构的动态特性[6]。由表4可见,自振频率的实测值和计算值基本相符。横向一阶实测频率为2.05 Hz,计算值为1.85 Hz;竖向一阶实测频率为3.03 Hz,计算值为2.99 Hz,说明结构有较高的横向和竖向刚度。实测一阶阻尼比为0.029 ,结构的阻尼系数较小, 振动衰减较慢。

表4 桥梁自振频率实测和计算值
3.2.2 行车试验结果与分析
无障碍行车工况下的实测冲击系数见图4。从图中可见,测试截面的无障碍行车冲击系数介于1.00~1.08之间,截面A-A行车冲击系数峰值为1.05,截面C-C行车冲击系数峰值为1.08,均出现在30 km/h车速,说明行车对桥梁结构的冲击作用较小。

图4 无障碍行车时各截面的动态响应与行车速度的关系
跳车工况下的实测冲击系数见图5。从图中可见,跳车冲击系数介于1.07~1.52之间,截面A-A、C-C跳车冲击系数峰值均为1.52,但截面A-A出现在车速20 km/h时,C-C出现在车速25 km/h时。跳车冲击系数较无障碍行车工况明显增大,说明当桥面凹凸不平时,车辆对桥梁将有显著的冲击作用,这与文献[7]的试验结果一致。
此外,截面A-A、截面C-C30 km/h制动冲击系数均为1.11,说明在该速度下车辆的制动作用力对桥梁结构的冲击作用不明显。以上行车工况的冲击系数均处于正常范围。

图5 跳车时各截面的动态响应与行车速度的关系
4 结论
静力荷载试验各工况下挠度结构校验系数和应力结构校验系数均处于合理范围内,该钢箱梁桥具有足够的刚度和强度,在各试验工况下均处于弹性工作状态。
该钢箱梁桥的自振频率实测值和计算值基本相符,横向和竖向基频较大,具有较高的横向和竖向刚度。
无障碍行车工况和30 km/h制动工况对桥梁结构的冲击作用较小;跳车工况冲击系数较无障碍行车工况明显增大。
[1] 张希黔,韦亮,张宏胜.城市钢箱梁结构立交桥的特点及安装技术[J].施工技术,2004,33(9)
[2] 章日凯,王常青.桥梁荷载试验[J].交通标准化,2005,(12):69-72
[3] 李国豪.桥梁结构稳定与振动[M].修订版.北京:中国铁道出版社,1992:256
[4] 刘羽宇,葛玉梅,杨翊仁.跨座式轻轨钢轨道梁的动力特性有限元分析[J].世界桥梁,2010,(1):41
[5] 刘羽宇,葛玉梅.尼尔森体系提篮拱桥自振特性分析[J]. 四川大学学报:工程科学版, 2008, 40(增刊): 86
[6] 贾艳敏,杨艳敏.齐齐哈尔嫩江公路大桥动载试验研究[J].公路交通科技,2000,17(增刊):61
[7] 刘羽宇,葛玉梅,高玉峰,等.厦门BRT一期工程钢箱梁桥静动载试验研究[J]. 铁道建筑,2010,(3):10

