图的双变量色多项式比较研究
刘 莹,唐晓清
(1.邵阳学院理学与信息科学系,中国 邵阳 422000;2.上海立信会计学院数学与信息学院,上海 201620)
图的双变量色多项式比较研究
刘 莹1,唐晓清2*
(1.邵阳学院理学与信息科学系,中国 邵阳 422000;2.上海立信会计学院数学与信息学院,上海 201620)
对图论的一些著名的双变量色多项式进行比较研究,对Tutte, Potts, Matching和Dohmen多项式,从定义、表达式的关系以及性质进行比较.特别地,对Tutte多项式的减-缩边公式,给出严格证明;对其余3种,则补充了它们各自的减-缩边公式以及证明.同时,由这些减-缩边公式得出它们各自一些特殊图的色多项式的具体计算公式,显示了减-缩边公式在简化计算方面的应用.
双变量色多项式;减-缩边公式;Pascal矩阵
色多项式一直是图论的一个重要研究方向.为了解决单变量色多项式中存在的一些问题,Tutte最先提出双变量色多项式[1],他的定义为:
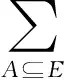
(1)
这里,G=(V,E),V和E分别表示图G的顶点集和边集,k(A)表示边子集A和V组成的子图(V,A)的连通部分数,k(E)表示图G的连通部分数,|A|表示边子集A所含边数,|V|表示顶点数.
其后,又陆续有一些学者提出一些新的双变量色多项式,比较著名的有Potts双变量色多项式,Matching双变量多项式等.最近,Dohmen等人提出新的双变量色多项式概念[2],并提出如下色多项式计算公式:

(2)
对于该新双变量色多项式,作者已经提出了相应的减-缩边公式[3],即:
P(G;x,y)=P(G-e;x,y)-P(G/e;x,y)+(x-y)·P(G-{u,v};x,y)
(3)
众所周知,减-缩边公式对色多项式的计算非常重要,本文对这些有代表性的双变量色多项式的减-缩边公式进行进一步的探讨.
1 Tutte双变量色多项式的减-缩边公式
Tutte双变量色多项式已提出很久了,但是,由于它的变量意义不太明显,故而,所引起的关注不很多.现在,本文尝试讨论有关问题.
定理1对于Tutte双变量色多项式,有如下减-缩边公式[4]:
(4)
注桥即有一个端点的度数为1的边.
证分如下三种情况:
Ⅰ.当边e是桥时,A=A′+{e},k(A)=k(A′),k(E)=k(E′)-1,|V|=|V′|+1,由式(1)有


Ⅱ.当边e是环时,A=A′+{e},k(A)=k(A′),k(E)=k(E′),|V|=|V′|,由式(1)有


Ⅲ.当边e非桥非环时,有如下两种情况:
当取边e时,A=A′+{e},k(A)+1=k(A′),k(E)+1=k(E′),|V|=|V′|;
当不取边e时,A=A′+{e},k(A)=k(A′),k(E)=k(E′),|V|=|V′|+1,由式(1)有

T(G-e;x,y)+T(G/e;x,y).
综合以上讨论可知,Tutte多项式的减缩边公式(4)恒成立.
减-缩边公式的应用
利用减-缩边公式(4),可方便地求得任何图的Tutte双变量色多项式.
(1) 有n个顶点的简单(没有重边和环)树图(表示为Tn),则有:
T(Tn;x,y)=xn-1,(n≥2).
(2) 有n个顶点的简单图圈(表示为Cn),则有:

(3) 对2个顶点之间有n条重边的图,称n连接图(Link)(表示为Ln), 则有:

注对于没有环的单个顶点,称为空图(Null)(表示为φ),令T(φ;x,y)=1.
(4) 对有n个顶点的扇图(表示为Fn), 则有:

一些简单的扇图的Tutte双变量色多项式如下:
T(F3;x,y)=y+x+x2,
T(F4;x,y)=y+x+y2+2xy+2x2+x3.
(5) 对有n个顶点的轮图(表示为Wn),则有:

[T(F3;x,y)+yT(L2;x,y)]+yn-4[T(F3;x,y)+yT(L2;x,y)+yT(L3;x,y)].
一些简单的轮图的Tutte双变量色多项式如下:
T(W4;x,y)=2y+2x+3y2+3x2+4xy+y3+x3,
T(W5;x,y)=3x+3y+9xy+6y2+4y3+y4+4xy2+6x2+4x2y+4x3+x4.
2 Potts剖分双变量色多项式
Potts双变量色多项式的表达式[6]如下:
(5)
同样,k(A)表示图G=(V,E)的边子集A和V组成的子图(V,A)的连通部分数,|A|表示边子集A所含边数.
比较(1)和(5),明显有:
T(G;x,y)=(x-1)-k(E)(y-1)-|V|·Z(G;(x-1)(y-1),y-1),
(6)
从定义(5),易得:Z(P1;x,y)=x,再令Z(φ;x,y)=1.
定理2对于Potts双变量色多项式计算公式,有如下减边公式:
Z(G;x,y)=Z(G-e;x,y)+y·Z(G/e;x,y)
(7)
证边e有两种情形:
Ⅰ.e∉A,此时,A=A′,k(A)=k(A′),|A|=|A′|;
Ⅱ.e∈A,此时,A=A′∪{e},k(A)=k(A′),|A|=|A′|+1.
综合这两种情形,故而:
Z(G-e;x,y)+y·Z(G/e;x,y).
一些特殊图的Potts色多项式计算公式
(1) 有n个顶点的路图(表示为Pn)的Potts色多项式的计算公式:
Z(Pn,x,y)=x·Z(Pn-1;x,y)+y·Z(Pn-1;x,y)=(x+y)·Z(Pn-1;x,y)=
(x+y)n-1·Z(P1;x,y)=x(x+y)n-1,n≥1.
(2) 有n个顶点的圈图(表示为Cn)的Potts色多项式的计算公式:
Z(Cn;x,y)=Z(Pn;x,y)+y·Z(Cn-1;x,y)=Z(Pn;x,y)+y·[Z(Pn-1;x,y)+y·Z(Cn-2;x,y)]=

而Z(C3;x,y)=x3+3x2y+3xy2+xy3,
经过反复迭代以后,可以得到圈图的计算公式:
(3) 对有n个顶点的扇图(表示为Fn),则有如下Potts计算公式:

[x3+4x2y+(x2y2+5xy2)+4xy3+xy4],n≥6.
下面是一些简单的扇图计算式
Z(F4;x,y)=x4+5x3y+10x2y2+2x2y3+8xy3+5xy4+xy5.
同样,圈图也有这样类似的表达式
3 Matching双变量色多项式
对于图G=(V,E),设|V|=n,ai是图G的i-匹配数[7],则匹配双变量色多项式为:
(8)
定理3对于匹配双变量色多项式,有如下减边公式:
M(G;x,y)=M(G-e;x,y)+yM(G-{u,v};x,y).
(9)
证由于边e=(uv),因此匹配数考虑两种情形:
Ⅰ.e∉M;
Ⅱ.e∈M,此时,顶点{u,v}饱和.
综合这两种情形,有

M(G-e;x,y)+y·M(G-{u,v};x,y).
一些特殊图的匹配色多项式计算公式
(1) 有n个顶点的路图(表示为Pn)的Matching色多项式的计算公式:
M(Pn;x,y)=x·M(Pn-1;x,y)+yM(Pn-2;x,y),并且,由于M(φ;x,y)=1;M(P1;x,y)=x迭代后可以得到任何路图的色多项式,下面是一些简单的路图计算式.
M(P2;x,y)=x2+y,M(P3;x,y)=x3+2xy.
(2) 有n个顶点的圈图(表示为Cn)的Matching色多项式的计算公式:
M(Cn;x,y)=M(Pn;x,y)+y·M(Pn-2;x,y),迭代后可以得到任何圈图的色多项式.下面是一些简单的圈图计算式.
M(C3;x,y)=x3+3xy,M(C4;x,y)=x4+4x2y+2y2.
(3) 对有n个顶点的扇图(表示为Fn),则有如下Matching色多项式计算公式:
M(Fn;x,y)=x·M(Fn-1;x,y)+y·M(Pn-2;x,y)+y·M(Fn-2;x,y),n≥5
并且,M(F3;x,y)=M(C3;x,y)=x3+3xy.下面是一些简单的扇图计算式
M(F4;x,y)=x4+5x2y+2y2,M(F5;x,y)=x5+7x3y+8xy2.
(4) 对有n个顶点的轮图(表示为Wn)的Matching色多项式的计算公式:
M(Wn;x,y)=M(Fn;x,y)+y·M(Fn-2;x,y),n≥5
下面是一些简单的轮图计算式
M(W4;x,y)=x4+6x2y+3y2,M(W5;x,y)=x5+8x3y+10xy2.
(5) 对有n个顶点的完全图(表示为Kn)的Matching色多项式的计算公式:
M(Kn;x,y)=x·M(Kn-1;x,y)+(n-1)y·M(Kn-2;x,y)
下面是一些简单的完全图计算式
M(K3;x,y)=x3+3xy,M(K4;x,y)=x4+6x2y+3y2.
(6) 对分别有m,n个顶点的完全二部图(表示为Km,n)的Matching色多项式的计算公式:
M(Km,n;x,y)=x·M(Km-1,n;x,y)+ny·M(Km-1,n-1;x,y)
下面是一些简单的完全二部图计算式
M(K3,2;x,y)=x5+6x3y+6xy2,M(K3,3;x,y)=x6+9x4y+18x2y2+6y3.
4 Dohmen双变量色多项式
我们已对Dohmen双变量色多项式得出了对应的减-缩边公式,详见文献[3].现在,本文对该公式给出新的证明.
定理4对于Dohmen新双变量色多项式计算公式,有如下减边公式[3]:
P(G;x,y)=P(G-e;x,y)-P(G/e;x,y)+(x-y)·P(G-{u,v};x,y) (10)
其中,顶点u∈V,v∈V,而且,边(uv)=e∈E
证由定义(2),有


即,有
P(G;x,y)=x[P(G-{u};x,y)+P(G-{v};x,y)]-y[P(G-{u};x,y)+P(G-{v};x,y)]+

P(G-{v};x,y)]-x[P(G-{u};x,y)+P(G-{v};x,y)-P(G-{u,v};x,y)]+
(x-y)[P(G-{u};x,y)+P(G-{v};x,y)]+(x-y)2P(G-{u,v};x,y)+

P(G-{v};x,y)+(x-y)P(G-{u,v};x,y)]=P(G-e;x,y)-P(G/e;x,y)+
(x-y)P(G-{u,v};x,y).
利用该减-缩边公式,易得一些特殊图的Dohmen色多项式计算公式[8-14].
(1) 对有n个顶点的完全图(表示为Kn)的Dohmen色多项式计算公式:
P(Kn;x,y)=yP(Kn-1;x-1,y-1)+(x-y)P(Kn-1;x,y).
(2) 对有n个顶点的轮图(表示为Wn)的Dohmen色多项式计算公式:
P(Wn;x,y)=yP(Cn-1;x-1,y-1)+(x-y)P(Cn-1;x,y).
(3) 对有n个顶点的路图(表示为Pn)的Dohmen色多项式的计算公式:

注对于没有顶点的空图φ,我们令P(φ,x,y)=1
(4) 对有n个顶点的圈图(表示为Cn)的Dohmen色多项式计算公式:

(5) 对分别有m,n个顶点的完全二部图(表示为Km,n)的Dohmen色多项式计算公式:

(6) 对有n个顶点的扇图(表示为Fn),则有如下DOHMEN色多项式计算公式:
P(Fn;x,y)=P(Wn;x,y)+P(Wn-1;x,y)-(x-y)·P(Fn-2;x,y) .
或者,有
P(Fn;x,y)=(x-2)·P(Fn-1;x,y)+(x-y)·[P(Fn-2;x,y)+P(Pn-2;x,y)].
5 结论
本文对于一些著名的双变量色多项式进行了比较研究,对有些定理给予新的证明,有些给出了相应的减缩边公式,此外,还探讨了它们之间的关系.期待这些工作能引起同行进一步的深入研究.
[1] TUTTE W T. Graph theory[M].Cambridge: Cambridge University Press, 2001.
[2] DOHMEN K, PÖNITZ A, TITTMANN P. A new two-variable generalization of the chromatic polynomial[J].Discrete Math Theor Comput Sci, 2003,6(2):69-89.
[3] 唐晓清,刘念祖,王汉兴,等.图的一类新双变量色多项式[J].兰州大学学报:自然科学版,2012,48(2):106-112.
[4] 唐晓清,刘念祖,王汉兴,等.正则树的双变量色多项式研究[J].应用数学学报,2013,36(4):761-768.
[5] 刘念祖,唐晓清,王汉兴.正则q-树根图的双概率可靠性探究[J].西南师范大学学报:自然科学版,2013,38(12):24-27.
[6] WELSH D. The Tutte polynomial[J].Random Structures Algorithms, 1999,15(3-4):210-228.
[7] AVERBOUCH I, MAKOWSKY J. The complexity of multivariate matching polynomials, January 2007. Preprint.
[8] 唐晓清,谭明纯.简单序约束条件下的参数估计的EM方法 [J].湖南工程学院学报,2010,20(1):61-64.
[9] 王汉兴,刘念祖,唐晓清,等.基于数学模型的混泥土泵车液压系统的Simulink动态仿真 [J].重庆理工大学学报:自然科学版,2012,26(9):1-7.
[10] 唐晓清,白延琴,刘念祖,等. 基于随机矩阵理论的Markowitz组合投资模型[J].上海大学学报:自然科学版, 2013,19(3):293-297.
[11] 沈小玲,侯耀平.最大度和次大度相等的双星树由它的Laplacian谱确定[J] .湖南师范大学自然科学学报, 2007,30(3):22-25.
[12] 沈小玲,侯耀平.毛毛虫图的r次幂的最小斜秩[J].湖南师范大学自然科学学报, 2014,37(4):87-91.
(编辑 胡文杰)
Comparison of Some Classes of Two-Variable Chromatic Polynomials
LIUYing1,TANGXiao-qing2,3*
(1.Department of Science and Information Science, Shaoyang University, Shaoyang 422000,China;2.School of Mathematics and Information, Shanghai Lixin University of Commerce,Shanghai 201620, China)
By comparing theTutte, Potts, Matching and Dohmen two-variable chromatic polynomials, the present work studied famous two-variable chromatic polynomials of graph. Their properties and the relationship between those definitions are investigated. Especially, a grid proof to reduce-contract edge formula of Tutte, as well as the others reduce-contract edge formulas and proofs are presented. Moreover, we studied some concrete compute formulas of special graphs to each of them based on those reduce-contract edge formulas, and those reduce-contract edge formulas show the application in simplifying calculation.
two-variable chromatic polynomial; reduce-contract edge formula; Pascal matrix
2013-03-26
国家自然科学基金资助项目(60872060)
*
,E-mail:tangxiaoqing5168@163.com
O157.5
A
1000-2537(2014)06-0067-06

