一种分享为有意义图像的(3,3)视觉密码方案
王洪君,牟晓丽,李静雪
(吉林师范大学计算机学院,中国 四平 136000)
一种分享为有意义图像的(3,3)视觉密码方案
王洪君*,牟晓丽,李静雪
(吉林师范大学计算机学院,中国 四平 136000)
给出了一种分享为有意义图像的(3,3)视觉密码方案,实现任意两个分享图像的叠加不能获得秘密图像的任何信息,而三个分享图像的叠加可以恢复秘密图像.实验结果证实了所给方案的有效性.
视觉密码;基本矩阵;分享;秘密图像
视觉密码是由Naor与Shamir在1994年的欧洲密码学年会上提出的一种图像分享技术[1],主要对二值图像进行加密及解密处理.其解密过程不需要计算机做复杂的运算,只需依赖人的视觉系统就可以直接恢复秘密图像.视觉密码相当于“一次一密”加密机制,具有很好的安全性,而且解密过程简单,因此引起了众多学者的关注.
视觉密码把秘密图像拆分为n个分享图像,每个分享图像的尺寸大小往往是秘密图像的m倍,m称为像素扩展度.针对像素扩展度大的问题,学者们提出了多种低像素扩展度的视觉密码方案[2-7],文献[2~3]提出了基于概率模型的像素不扩展可视秘密方案,该方案根据黑白像素点在黑白区域出现概率的不同来区分黑白区域;文献[4]提出基于递归算法的像素不扩展的视觉密码方案,之后对其进行改进提出最佳对比度的像素不扩展视觉密码方案[5].对比度是衡量视觉密码方案优劣的一项指标,对比度高恢复出的图像清晰,对比度低恢复出的图像模糊,文献[7~9]提出了对比度优化的视觉密码方案构造方法.文献[8~9]提出基于反转操作的提高图像对比度的像素不扩展方案,具有很好的效果.最初的视觉密码主要是对二值图像进行加密,目前有许多学者把这一技术应用于灰度和彩色图像,研究灰度图像和彩色图像的视觉密码技术[10-12].视觉密码在恢复秘密信息时,如果参与者出示了虚假的分享图像,那么就不能恢复秘密信息或者恢复出错误的图像,也可能导致欺骗者获得足够数量的分享图像,从而恢复秘密图像.文献[13~16]提出了防欺骗的视觉密码, 可以有效地检测欺骗行为的发生.为了便于管理多个秘密图像,多秘密分享视觉密码[17-20]的思想被提出,不仅可以解决分享多幅图像带来的共享份管理问题,还可广泛地应用于信息的分级管理、共享的身份认证等方面[17].由于分享图像通常表现为噪声形式,容易引起攻击者的怀疑,从而受到安全威胁,因此,有学者提出分享图像为有意义图像的视觉密码[21-24].
本文基于文献[1]的视觉密码扩展方案,给出一种分享为有意义图像的(3,3)视觉密码方案,将分享图像隐藏在有意义的图像中,这样分享图像就是一幅有意义的图像,不易引起攻击者的怀疑.该方案中任意两个分享图像的叠加结果为毫无意义的图像,不能泄露秘密图像的任何信息,而三个分享图像的叠加可以恢复秘密图像.
1 视觉密码
1.1 视觉密码方案
Naor和Shamir提出的可视密码技术基于秘密分享的思想,把秘密图像分成n份(称为分享份)分给n个参与者,任意k个或k个以上的参与者可以恢复秘密图像,而小于k个参与者的分享份的任意组合都不能获得任何有关秘密图像的信息.Naor和Shamir通过构建基本矩阵的方法构造了 (k,n)视觉密码方案[1].其基本矩阵为一n×m阶布尔矩阵,其中用逻辑值“1”代表黑色,用逻辑值“0”代表白色,n为参与者人数,m为像素扩展度,即秘密图像上的每个像素对应到分享图上扩展为m个子像素. (k,n)视觉密码方案生成的分享图像都是黑白像素点随机分布的毫无意义的图像.解密过程只需把这些分享图印到透明胶片上,然后让其中的k个或k个以上胶片叠加,通过人的视觉即可恢复秘密图像.这样所生产的分享图像和解密出来的秘密图像都是原图像的m倍.
1.2视觉密码扩展方案
最初视觉密码的分享图像是黑白像素点随机分布的毫无意义的图像,扩展方案用有意义的图像掩盖分享图像使得分享为一幅有意义的图像.文献[1]对(2,2)视觉密码方案进行了扩展,使得分享为有意义的图像,所给方案如图1所示.如果秘密图像是白像素点,可以选用上面一行中的某个分享方案;如果秘密图像是黑像素点,可以选用下面一行中的某个分享方案.

(a)两个白色分享 (b)白色和黑色分享 (c)两个黑色分享

(d)两个白色分享 (e)白色和黑色分享 (f)两个黑色分享
图1所示分享方案对应的基本矩阵为:
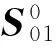
2 分享份为有意义图像的(3,3)视觉密码方案
2.1 方案构建方法
通过研究上述1.2视觉密码扩展方案不难发现,如果掩盖图像为白像素点,其对应的4个子像素中有两个“0”,如果掩盖图像为黑色像素点,其对应的4子像素中只有一个“0”.而基本矩阵两行叠加的结果是,如果秘密图像为白色像素,4个子像素中只有一个“0”;如果秘密图像为黑色像素,4个子像素中全是“1”.基于这样的思想,对于分享为有意义图像的(3,3)视觉密码方案,我们考虑如果掩盖图像为白色像素点,对应的基本矩阵的相应行就应该至少有两个“0”;如果掩盖图像为黑色像素点,对应的基本矩阵的相应行就应该有至少一个“0”:也就是说掩盖图像中白色像素点对应的子像素比黑色像素点对应的子像素含有更多的白色子像素.基本矩阵的任意两行叠加有相同个数的“0”,这样就保证了任意两个分享图像叠加的结果是不可区分的.如果秘密图像像素为白色,则基本矩阵的三行“或”运算的结果含有一个“0”;如果秘密图像像素为黑色,基本矩阵三行“或”运算的结果就全是“1”.基于这样的思想构建的基本矩阵为:
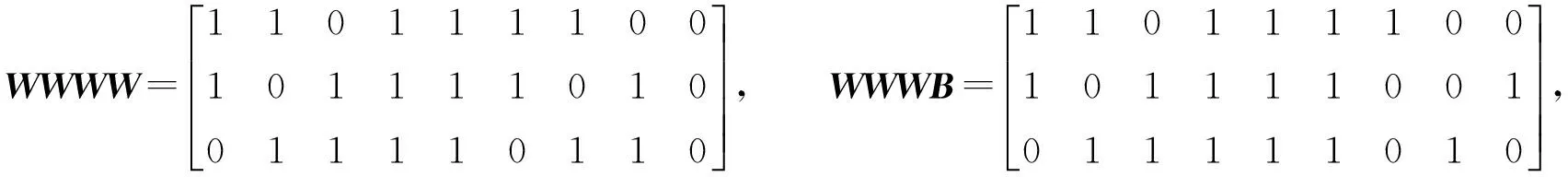



如果秘密图像像素是“白”色,分享由WWWW,WBWW,WBBW,BBBW4个基本矩阵之一产生;秘密图像像像素如果是“黑”色,分享由WWWB,WBWB,WBBB,BBBB4个基本矩阵之一产生.
以基本矩阵WBWB为例,含义为:W代表“白”,B代表“黑”,第一个字母W表示掩盖图像1为白色像素点,第二个字母B表示掩盖图像2为黑色像素点,第三个字母W表示掩盖图像3为白色像素,最后一个字母B表示三行“或”运算的结果为黑色像素,即秘密图像为黑像素.
基本矩阵实际应该有16个,分别是WWWW,BWWW,WBWW,WWBW,WBBW,BWBW,BBWW,BBBW,WWWB,BWWB,WBWB,WWBB,WBBB,BWBB,BBWB,BBBB,这里只给出了8个,其他几个可以通过相应的基本矩阵作行变换得到.例如:基本矩阵BWWW,WWBW可由基本矩阵WBWW作行变换得到.
2.2 实验分析
2.2.1 算法实现
输入:三幅掩盖图像、一幅秘密图像
输出:三幅分享图像
步骤:
(1) 产生一个关于向量(1,2,3,…,9)的随机置换π.
(2) 如果秘密图像像素g是一个白色像素,那么对基本矩阵WWWW,BWWW,WBWW,WWBW,WBBW,BWBW,BBWW,BBBW之一作列置换π,得到矩阵T;秘密图像像素g如果是黑色像素,那么对基本矩阵WWWB,BWWB,WBWB,WWBB,WBBB,BWBB,BBWB,BBBB之一作列置换π,得到矩阵T.
(3) 对1≤i≤3,分配矩阵T的第i行给第i个参与者.
2.2.2 实验结果
实验中所用图像如图2所示,实验结果如图3所示.

掩盖图像1 掩盖图像2 掩盖图像3 秘密图像

分享图像1 分享图像2 分享图像3 两个分享图叠加结果 恢复的秘密图像
2.2.3 结果分析
实验结果表明,3个分享图像分别显示了不同的信息,有别于传统视觉密码方案.实验中生产的分享图像的扩展度为9,这是为了保持原始图像的纵横比.实际上研究基本矩阵会发现,基本矩阵包含一个共同的两个全都是“1”的列,这样的两列可以去掉,这样分享图像的扩展度就是7.比基于矩阵连接的方案[22](其扩展度为8)具有更小的扩展度.由于基本矩阵的任意两行“或”运算的结果向量都只含有一个“0”,所以不会暴露秘密图像的任何信息.从实验结果可以看出,两幅分享图像的叠加为毫无意义的二值图像,没有暴露秘密图像的任何信息,所以所给方案具有很好的安全性.3幅分享图像的叠加恢复了秘密图像,实验结果表明所给方案是有效的.
3 结论
本文给出了一种分享为有意义图像的(3,3)视觉密码方案,使得分享图像被有意义的图像掩盖,产生分享为有意义的图像.从实验结果可以看出所给方案是有效的,分享为有意义的图像,任意两个分享图像的叠加不能恢复秘密图像,而3个分享图像的叠加可以恢复秘密图像.实验结果表明所给方案简单可行,所给方案适用秘密图像为文本、标识等二值图像.进一步的工作将对改善分享图像和所恢复的秘密图像的质量、减少像素扩展度等方面作更深入的研究.
[1] NAOR M, SHAMIR A. Visual cryptography[C]. Advances in Cryptology-Eurocrypt’94, May 9-12, Italy, 1994. Berlin: Springer-Verlag, 1995, LNCS950:1-12.
[2] ITO R, TANAKA H. Image size invariant visual cryptography[J]. IEICE Trans. Fundamentals,1999, E822A(10):2172-2177.
[3] YANG C N. New visual secret sharing schemes using probabilistic method[J]. Patt Recog Lett, 2004,25(4):481-494.
[4] LIN T L, HORNG S J, LEE K H,etal. A novel visual secret sharing scheme for multiple secrets without pixel expansion[J]. Expert Sys Appl, 2010,37(12):7828-7869.
[5] LIN S J, LIN J C, FANG W P. Visual Cryptography (VC) with Non-expanded shadow images: hilbert-curve approach[C]. Taipai, 2008. Piscataway, N J: IEEE Press, 2008.
[6] MONOTH T, ANTO B P. Recursive visual cryptography using random basis column pixel expansion[C]. Proceeding of the IEEE International Conference on Information Technology, Orissa Dec 17-20, 2007. California: IEEE Computer Society Press, 2007:41-43.
[7] MONOTH T, ANTO B P. Achieving optimal contrast in visual cryptography schemes without pixel expansion[J]. Int J Recent Trends in Eng, 2009,1(1):468-471.
[8] CIMATO S, SANTIS A D,etal. Ideal contrast visual cryptography schemes with reversing [J]. Infor Proc Lett, 2005,93 (4):199-206.
[9] 张海波,王小非,徐海樵,等. 利用反转实现理想对比度的密图分存[J]. 电子学报, 2010,38(2):465-468.
[10] KANDAR S, MAITI A.k-nSecret sharing visual cryptography scheme for color image using random number[J]. Int J Eng Sci Tech, 2011,3(3):1851-1857.
[11] YANG C N, CHEN T S. Colored visual cryptography scheme based on additive color mixing[J]. Patt Recog, 2008,41(10):3114-3129.
[12] 易 枫,王道顺,戴一奇. 彩色图像的可视分存方案[J]. 计算机辅助设计与图形学学报, 2006,18(11):1770-1775.
[13] LIU F, WU C K. Cheating immune visual cryptographyscheme[J]. IET Inform Secur, 2011,5(1):51-59.
[14] 陈 勤,彭文芳,徐 坤,等.基于排列组合的可防欺骗视觉密码方案[J] .计算机应用研究,2011,28(1):318-321.
[15] 郁 滨,卢锦元,房礼国. 基于迭代算法的可验证视觉密码[J]. 电子与信息学报, 2011,33(1):163-167
[16] 郁 滨,王益伟,房礼国.基于概率法的防欺骗视觉密码方案[J].计算机应用,2009,29(7):1782-1784.
[17] 付正欣, 郁 滨, 房礼国.一种新的多秘密分享视觉密码[J]. 电子学报, 2011,39(3):714-718.
[18] 付正欣,郁 滨,房礼国. 基于环形共享份的多秘密视觉密码[J]. 电子与信息学报,2010,32(4):880-883.
[19] 王益伟, 郁 滨, 付正欣, 等. 像素不扩展的防欺骗视觉密码方案研究[J]. 解放军信息工程大学学报,2011,12 (2):149-153.
[20] 沈 刚,付正欣,郁 滨. 基于XOR 的( 2,2,n) 多秘密视觉密码[J],计算机应用研究,2012,29(10):3797-3799.
[21] LIU F, WU C K. Embeded extended visual cryptography schemes[J]. IEEE Trans Inform Foren Secur, 2011,6(2):307-322.
[22] WANG D S, YI F, LI X B. On general construction for extended visual cryptography schemes[J]. Patt Recog, 2009,42(11):3071-3082.
[23] 牛冬梅.具有掩盖图像的(2,2)可视密码方案[J]. 通信技术, 2009,42(7):82-84.
[24] 付正欣,郁 滨,房礼国.具有伪装图案的操作式多秘密视觉密码[J]. 计算机科学, 2011,38 (6):90-92.
(编辑 胡文杰)
A(3,3)Visual Cryptography Scheme Using Meaningful Shares
WANGHong-jun*,MUXiao-li,LIJing-xue
(College of Computer, Jilin Normal University, Siping 136000, China)
A(3,3)visual cryptography scheme using meaningful shares was presented, in which nothing can be gained about the secret image by stacking two shares together while the secret image could be recovered by stocking three shares together. Experimental results confirm the effectiveness of the proposed scheme.
visual cryptography; basic matrix; share; secret image
2013-02-27
国家自然科学基金资助项目(31070224);吉林省教育厅“十二五”科学技术研究资助项目(吉教科合字[2011]第162号)
*
,E-mail:jlnuwhj@sina.com
TN911.73
A
1000-2537(2014)06-0079-05

