电感电流伪连续模式下Boost变换器的分数阶建模与分析∗

谭程 梁志珊

(中国石油大学(北京),地球物理与信息工程学院,北京 102249)

1 引 言

虽然分数阶微积分理论拥有与整数阶微积分几乎一样长的研究历史,但由于缺乏明显的几何意义,使其应用一时受到了限制.直到近年来,在机械、物理、工程、信息科学、材料科学等领域发现存在分数阶现象,使得分数阶微积分理论有了实际的应用背景,从而成为了物理学和工程学的研究热点[1−3].整数阶微积分是相应分数阶微积分的特例情况[4].已有的研究表明,相比于整数阶的系统模型,其分数阶模型能更透彻、更准确的反映系统的物理现象[5].

近年来,对电感和电容数学建模的研究结果表明:电感和电容本质上都是分数阶的[6],整数阶的电感和电容在实际中并不存在,基于分数阶微积分理论建立的电感和电容模型更能反映其电特性[7,8],以往用来描述电感和电容电特性的整数阶模型是不够准确的甚至可能是错误的.然而,电感和电容又是开关功率变换器电路中不可或缺的电子器件.以往对开关功率变换器的模型研究都是建立在电感和电容是整数阶基础上的,显然这与其分数阶的本质是相违背的,是不科学的,这不能准确的反映开关功率变换器的动力学特性甚至可能会得出错误的结论.在已有的研究中,文献[9]分析了分数阶电容对功率因数校正变换器的影响,却没有考虑电感也是分数阶的.文献[10]所建立的分数阶Buck-Boost变换器的模型也仅考虑了电容是分数阶的.鉴于电感和电容本质上都是分数阶的事实,文献[11]对工作于电感电流连续模式(continuous conduction mode,CCM)下的Boost变换器进行了分数阶区间数学模型和分数阶状态平均模型的建立和分析,但没有进行电路模型的仿真验证且分数阶CCM Boost变换器的控制输出传递函数具有右半平面零点(right half plane,RHP)问题;文献[12]对工作于电感电流断续模式(discontinuous conduction mode,DCM)下的Boost变换器进行了分数阶区间数学模型和分数阶状态平均模型的建立和分析,但也没有进行电路模型的仿真验证且分数阶DCM Boost变换器有电感电流纹波大、带负载能力弱等问题.而工作于电感电流伪连续模式(pseudo continuous conduction mode,PCCM)下的Boost变换器(又称三态Boost变换器)具有比CCM模式和DCM模式变换器更优良的工作性能[13].PCCM是一种介于CCM和DCM之间,Boost变换器的第三种工作模式[14].相对于CCM Boost变换器,PCCM Boost变换器的控制输出传递函数不存在RHP问题,提高了系统的闭环稳定性和动态响应性能;相对于DCM Boost变换器,PCCM Boost变换器具有电感电流纹波小、带负载能力强的优点.因此,对PCCM Boost变换器的分数阶模型的研究是一项具有重要理论意义和实际应用价值的课题.

本文以PCCM Boost变换器为研究对象,推导出了PCCM Boost变换器的分数阶区间数学模型和分数阶状态平均模型,对其电感电流和输出电压进行了理论分析以及传递函数的推导,并基于Matlab/Simulink的仿真环境,通过对推导的数学模型和电路模型进行仿真,分析了模型误差产生的原因,验证了分数阶建模与理论分析的正确性.最后,指出了分数阶Boost变换器工作于电感电流伪连续模式与连续模式、断续模式的区别与联系.

2 PCCM Boost变换器的分数阶区间数学建模及分析

根据文献[8]可知,分数阶电感和分数阶电容的数学模型为

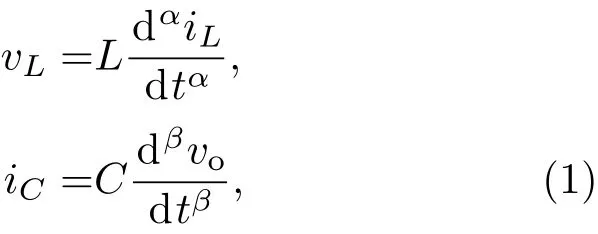
其中,iL为流过分数阶电感的电流,vL为分数阶电感两端的电压,L为分数阶电感值,iC为流经分数阶电容的电流,vo为分数阶电容两端的电压,C为分数阶电容值,α和β分别为电感和电容的分数阶阶数且0＜α,β＜1.

Boost变换器工作于电感电流伪连续模式下的电路原理图和时序脉冲及电感电流波形,如图1所示.其中,vin为输入电压,R为负载电阻,PS1为控制开关管S1通断的周期性脉冲信号,PS2为控制开关管S2通断的周期性脉冲信号,周期均为T.则PCCM Boost变换器的工作原理为

1)工作模态1(0＜t＜d1T):周期性脉冲信号PS1为高电平,PS2为低电平时,开关管S1导通、S2关断,二极管Di1承受反向电压而关断,持续时间为d1T.

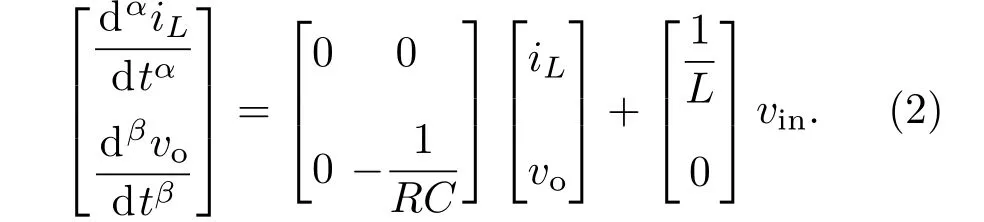
2)工作模态2(d1T＜t＜(d1+d2)T):周期性脉冲信号PS1为低电平,PS2为低电平时,开关管S1关断、S2关断,二极管Di1承受正向电压而导通,持续时间为d2T.

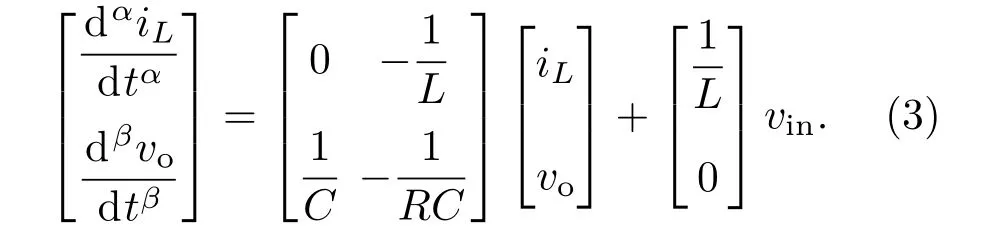
3)工作模态3((d1+d2)T＜t＜T):周期性脉冲信号PS1为低电平,PS2为高电平时,开关管S1关断、S2导通,二极管Di1承受反向电压而关断,持续时间为d3T,其中d1+d2+d3=1.

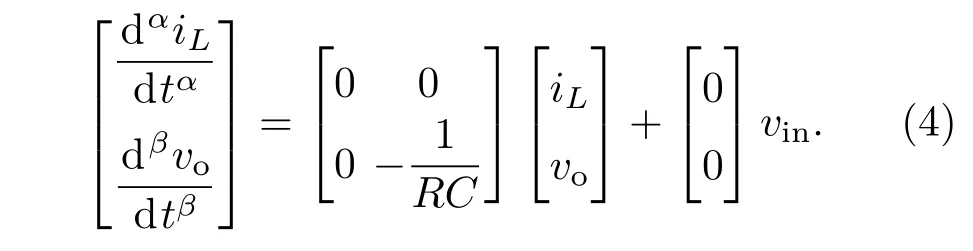
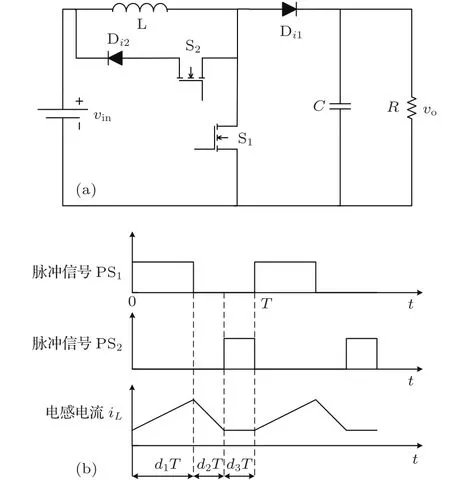
图1 PCCM Boost变换器 (a)电路原理图;(b)时序脉冲及电感电流波形图

3 PCCM Boost变换器分数阶状态平均模型的建立与分析

3.1 PCCM Boost变换器分数阶状态平均模型的建立

根据状态平均法、PCCM Boost变换器三个工作模态的特点及分数阶微积分的性质[15],对(2),(3),(4)式在一个工作周期T内求平均,可推导得到工作于电感电流伪连续模式下的状态平均模型为

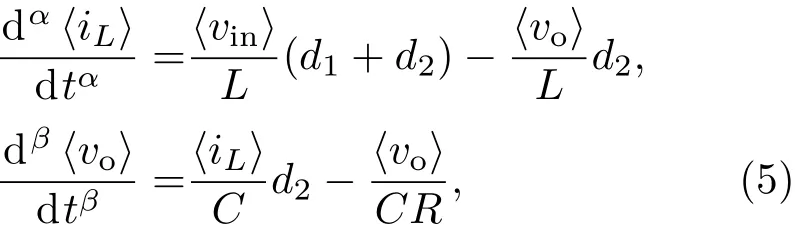
其中,〈vin〉,〈vo〉,〈iL〉分别为vin,vo,iL在一个周期内的平均值,令Vin,Vo,IL,D1,D2分别为vin,vo,iL,d1,d2的直流分量,ˆvin,ˆvo,ˆiL,ˆd1,ˆd2分别为vin,vo,iL,d1,d2的交流分量.因此,可对ˆvin,ˆvo,ˆiL,ˆd1,ˆd2作如下分解:

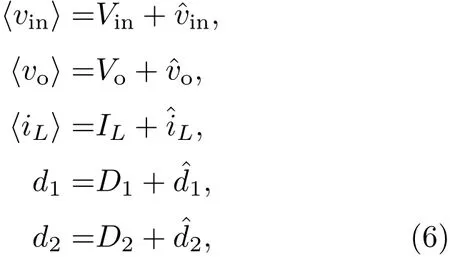
且

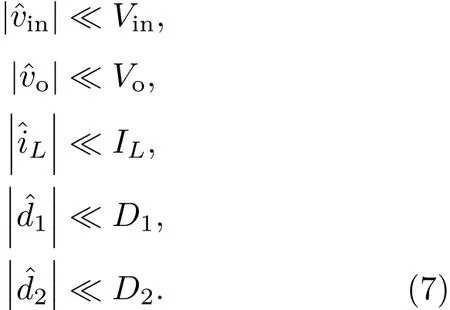
3.2 PCCM Boost变换器分数阶状态平均模型的分析

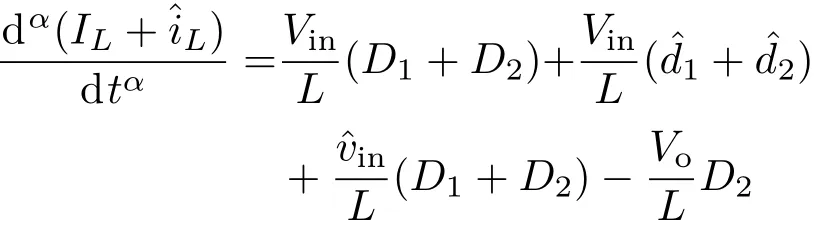
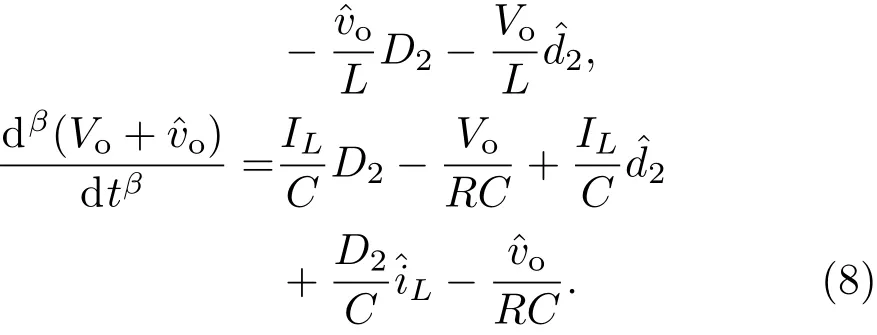
将(8)式中的直流分量分离出来,可得

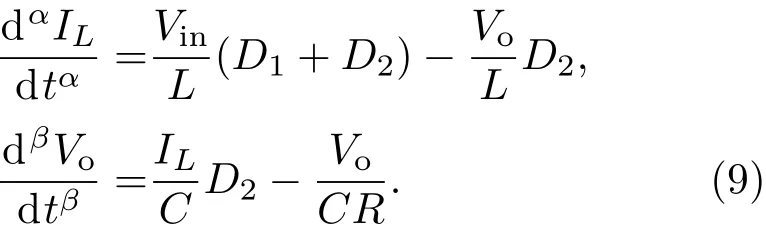
根据Caputo分数阶导数定义可知[15],常数的任意分数阶导数等于零,则由(9)式可得系统处于稳态时的工作点为

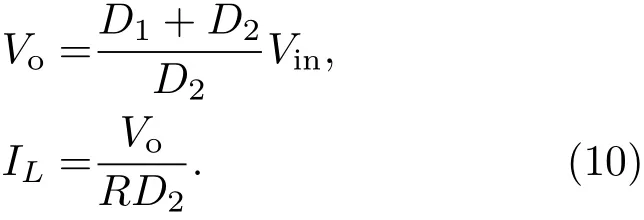
此外,根据Caputo分数阶导数定义,由(2)式可求得电感电流iL在(0,d1T)时间内的增加量,即电感电流纹波∆iL为

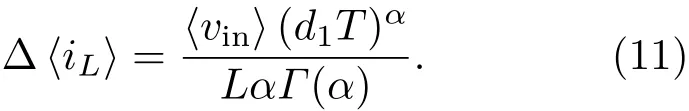
将(6)式代入(11)式且忽略高阶小量,并将其直流分量分离后,可得

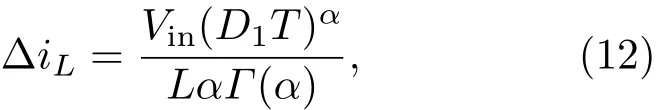
其中,Γ(·)为伽马函数[15].可见,电感电流纹波∆iL不仅与电感L、输入电压直流分量Vin、占空比直流分量D1以及开关周期T有关,而且还与电感的阶数α有关,并且与电感的阶数α成反比例关系.与此同时,当α=1时,(12)式与用整数阶模型所求的结果一致.

根据(10)式和(12)式可求得电感电流峰值iL−max和谷值iL−min的表达式分别为

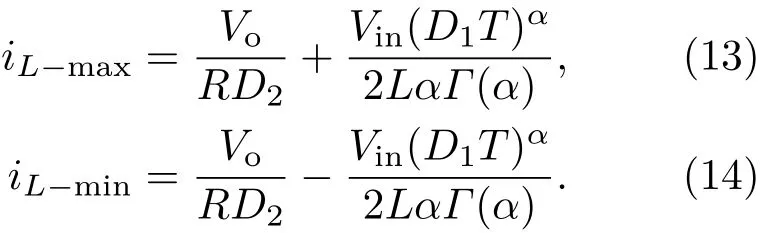
由于PCCM Boost变换器独特的工作模式,使其在工作模式1和工作模式3时,输出电压vo均处于下降过程,因此可知输出电压纹波∆vo为

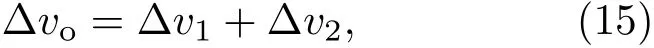
其中,∆v1为处于工作模式1时的电压减少量,∆v2为处于工作模式3时的电压减少量.

同理,根据(2)式和(4)式可求得输出电压vo在(0,d1T)和((d1+d2)T,T)时间内的减少量,即输出电压纹波∆vo为

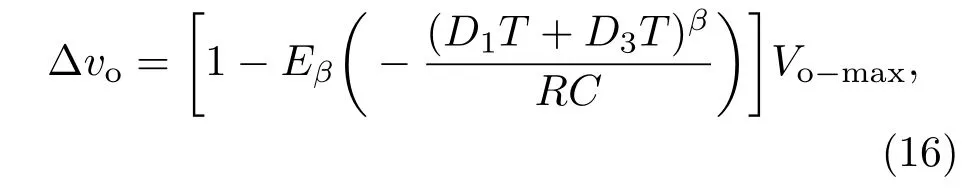
其中,Eβ(·)为Mittag-Leラe函数[15],Vo−max为输出电压峰值,其表达式为

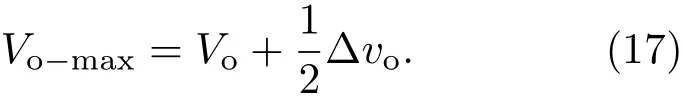
将(10)式和(16)式代入(17)式可得

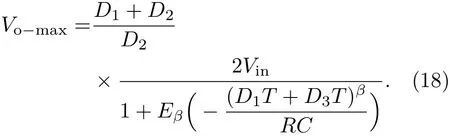
将(18)式代入(16)式可得电压输出纹波表达式为

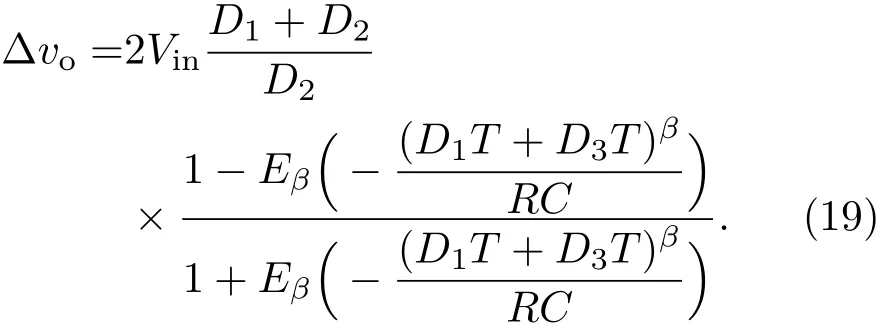
根据电路模型和数学模型的电感电流iL和输出电压vo,可得所建数学模型的误差百分比为

其中,bfbi为电感电流模型误差百分比,bfbv为输出电压模型误差百分比,iLd和vod分别为电路模型的电感电流和输出电压,iLs和vos分别为数学模型的电感电流和输出电压.

可见,输出电压纹波∆vo不仅与电容C、输入电压直流分量Vin、占空比直流分量D1,D2,D3、负载电阻R以及开关周期T有关,而且还与电容的阶数β有关,并且与电感的阶数β成反比例关系.与此同时,当β=1时,(19)式与用整数阶模型所求的结果一致.

3.3 PCCM Boost变换器分数阶传递函数的分析

将(8)式的交流分量分离出来,可得

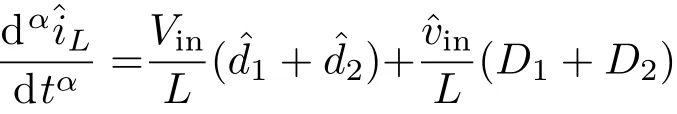
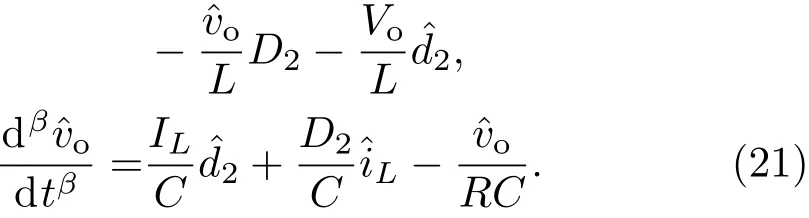
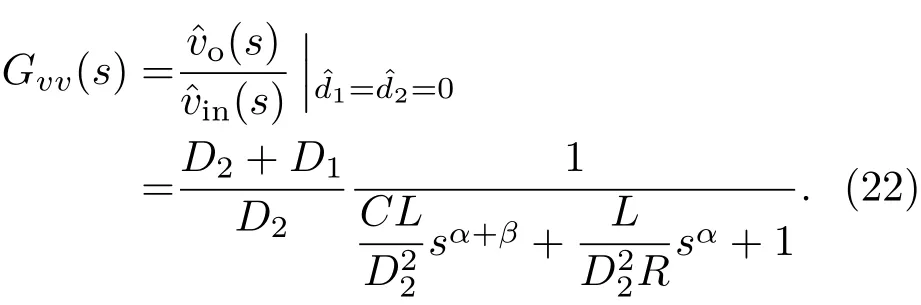
(22)式表明当占空比d1,d2的扰动变量==0时,输入电压vin的变化对输出电压vo的影响.

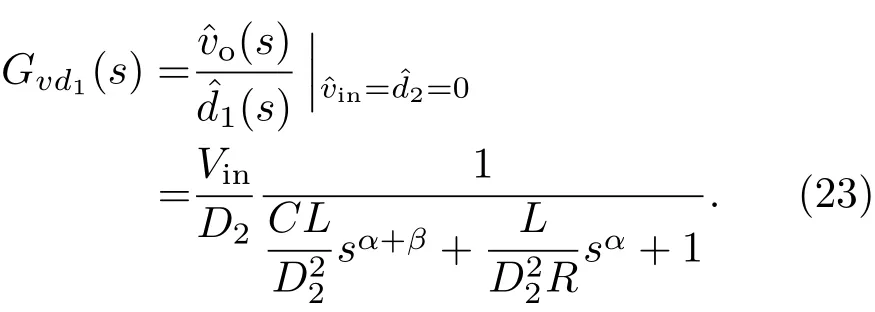
(23)式表明当输入电压vin的扰动变量=0,占空比d2的扰动变量=0时,占空比d1的变化对输出电压vo的影响.

输出电压ˆvo对占空比的传递函数Gvd2(s)为

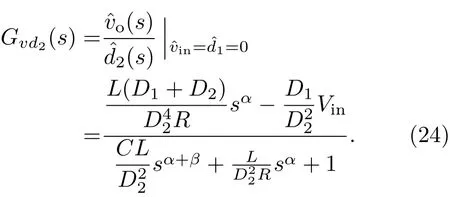
(24)式表明当输入电压vin的扰动变量=0,占空比d1的扰动变量=0时,占空比d2的变化对输出电压vo的影响.

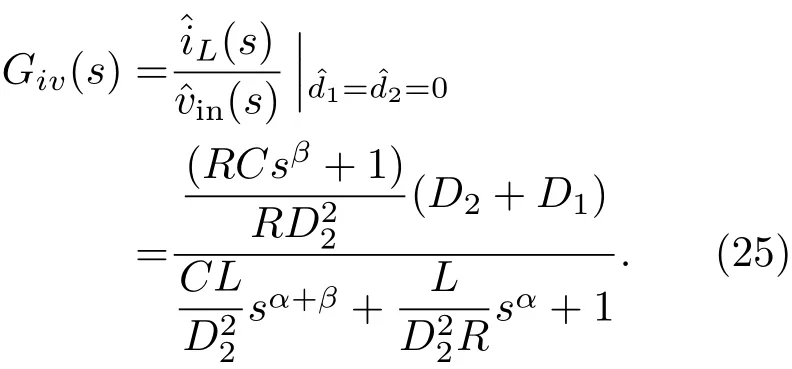
(25)式表明当占空比d1,d2的扰动变量==0时,输入电压vin的变化对电感电流iL的影响.

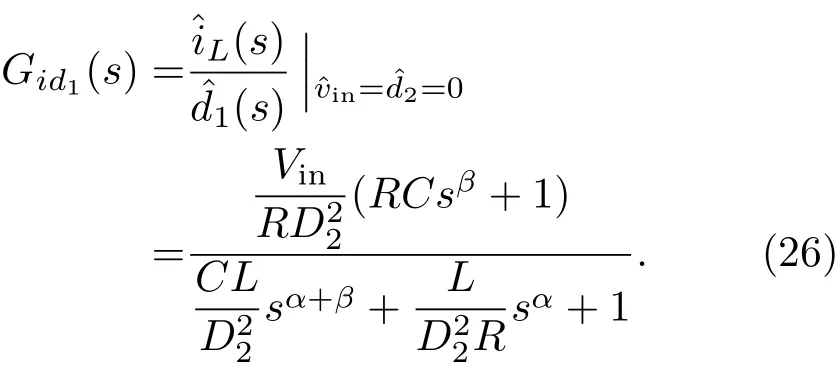
(26)式表明当输入电压vin的扰动变量=0,占空比d2的扰动变量=0时,占空比d1的变化对电感电流iL的影响.

输出电流ˆiL对占空比的传递函数Gid2(s)为

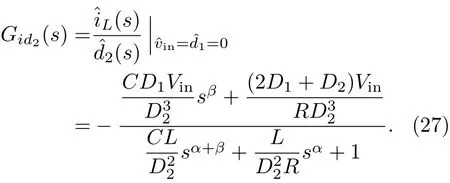
(27)式表明当输入电压vin的扰动变量=0,占空比d1的扰动变量=0时,占空比d2的变化对电感电流iL的影响.

根据(23)式可知,分数阶PCCM Boost变换器的控制输出传递函数不存在RHP问题.当电感和电容的分数阶阶数α,β都等于1时,(22)–(27)式所示的分数阶传递函数与文献[14,16]所描述的整数阶传递函数相一致,进一步说明了整数阶系统是其分数阶系统的特例情况,且在频域和时域响应中,α,β这两个参数对PCCM Boost变换器系统的动力学特性也产生了极大的影响.

4 数值仿真

4.1 分数阶电感和电容的等效电路模型

根据文献[17],基于分抗链[15]和改进的Oustaloup滤波器的分数阶微积分算法[18],可以得到分数阶电感和分数阶电容的等效电路模型,如图2和图3所示.当Lα=3 mH,α=0.8时,图2中各电阻值分别为RL1=7.16 kΩ,RL2=340.84 Ω,RL3=34.25 Ω,RL4=3.54 Ω,RL5=367 mΩ,RL6=38 mΩ,RL7=4 mΩ,RL8=0.4 mΩ,RL9=42µΩ,RL10=5µΩ;各电感值分别为L1=95µH,L2=77µH,L3=131.6µH,L4=231.6 µH,L5=408 µH,L6=719.4 µH,L7=1.268 mH,L8=2.235 mH,L9=3.934 mH.当Cβ=100µH,β=0.8时,图3中各电阻值分别为RC1=20 mΩ,RC2=160 mΩ,RC3=1.5 Ω,RC4=14.6 Ω,RC5=141 Ω,RC6=1.36 kΩ,RC7=13.131 kΩ,RC8=126.742 kΩ,RC9=1.222 MΩ,RC10=102.85 MΩ;各电容值分别为C1=6.5µF,C2=13.98µF,C3=24.5µF,C4=43.2 µF,C5=76.2 µF,C6=134.2 µF,C7=236.6 µF,C8=417 µF,C9=736 µF,C10=560µF.

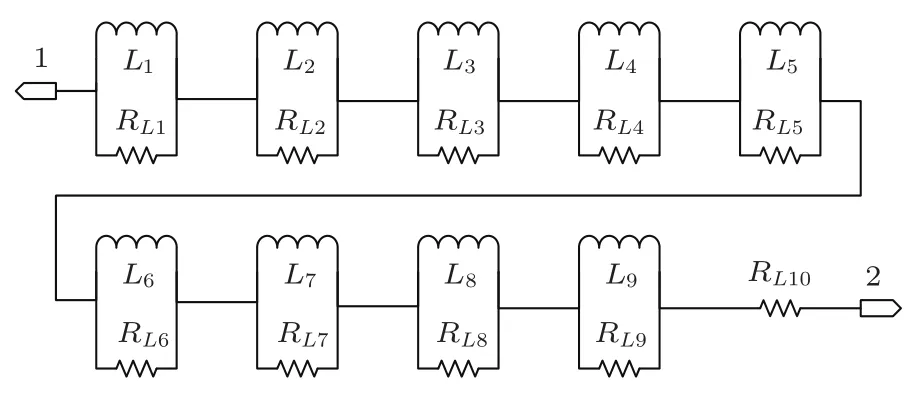
图2 分数阶电感等效电路模型

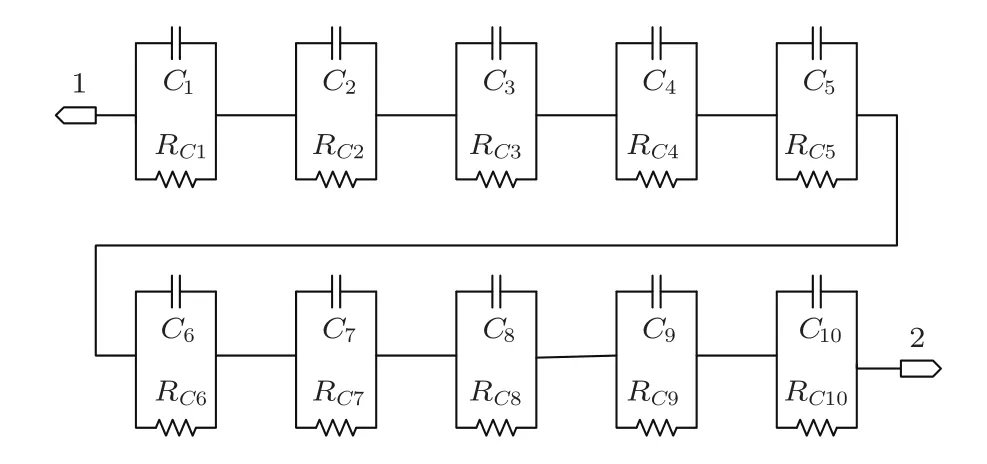
图3 分数阶电容等效电路模型

4.2 分数阶PCCM Boost变换器的状态平均模型与电路模型的仿真对比

文献[11]和文献[12]虽然分别建立了分数阶CCM Boost变换器的数学模型和分数阶DCM Boost变换器的数学模型,并进行了仿真,但由于PCCM Boost变换器独特的工作模式,使得文献[11]和文献[12]所建立的仿真数学模型并不能适用于PCCM Boost变换器的数学模型仿真.因此,必须根据PCCM Boost变换器自身的特点,并根据文献[18]所提出的改进的Oustaloup滤波器的分数阶微积分算法和(5)式重新构建Matlab/Simulink数学模型,如图4所示.其中,Fractional Ints−α为分数阶积分单元,其内部结构如文献[11]所示.在改进的Oustaloup滤波器的分数阶微积分算法中,存在三个关键参数:拟合频率下限ωb、拟合频率上限ωh、滤波器阶数2N+1.而在对实际分数阶系统进行数值仿真时,需根据系统的频率范围选择拟合频率段(ωb,ωh)和N 值,一般取ωb·ωh=1. 选取电路参数为vin=24 V,L=3 mH,C=100µF,d1=0.4,d2=0.2,f=50 kHz.由于开关频率f=50 kHz,即ω =2πf=3.14× 105rad/s,考虑还有高于开关频率的高频谐波存在,因而拟合频率的选取需满足条件ωh＞3.14×105rad/s.因此,选取ωh=1×106rad/s,ωb=1×10−6rad/s,N=10.根据分数阶电感和电容的等效电路模型所建立的电路仿真模型,如图5所示.

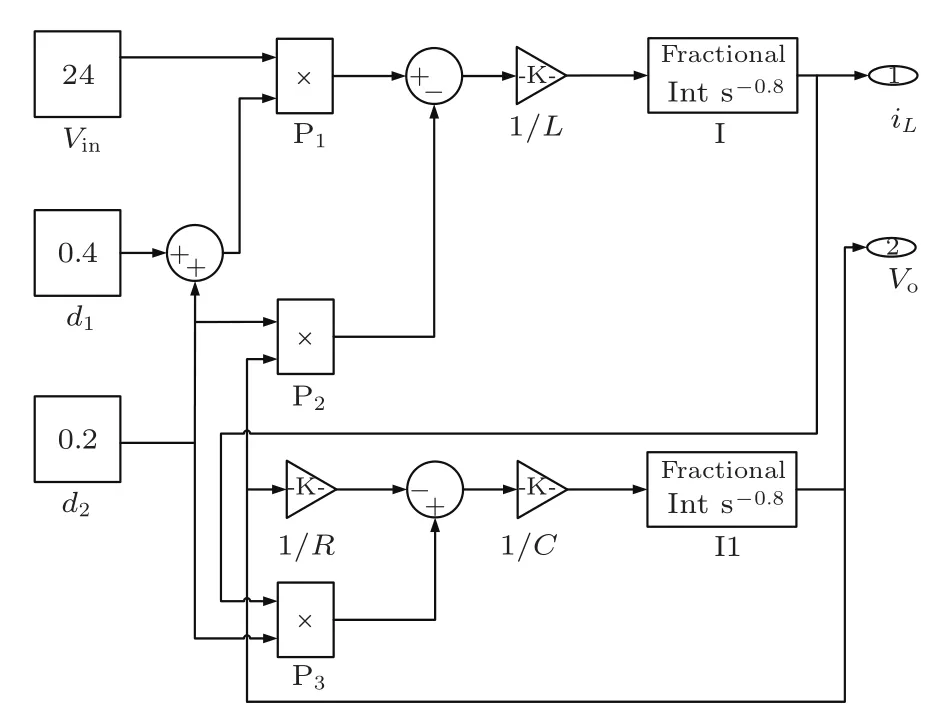
图4 分数阶PCCM Boost变换器Simulink数学仿真模型

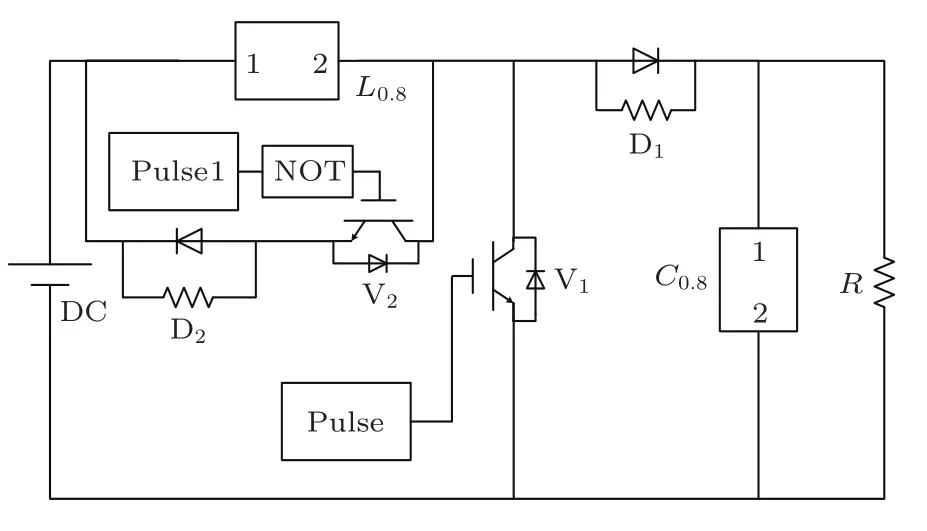
图5 分数阶PCCM Boost变换器Simulink电路仿真模型

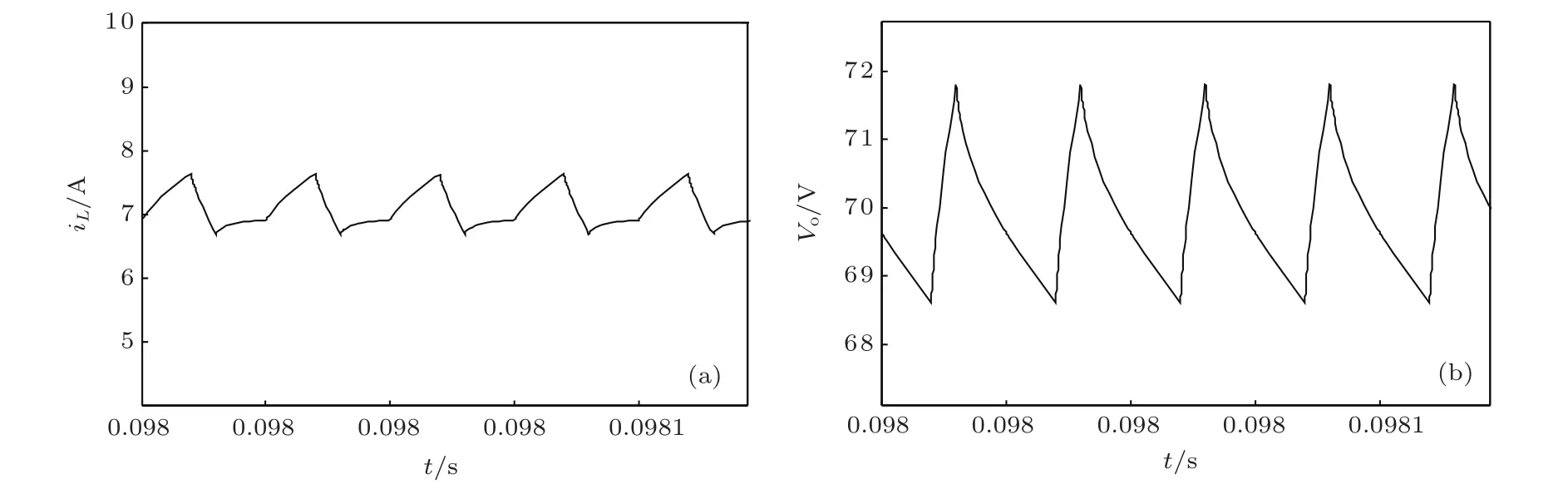
图6 分数阶PCCM Boost变换器电路模型仿真波形(a)电感电流iL;(b)输出电压vo

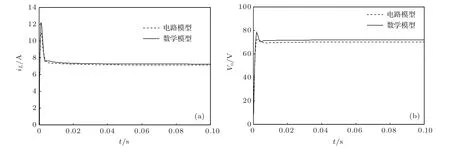
图7 分数阶PCCM Boost变换器电路模型与数学模型仿真波形比较 (a)电感电流iL;(b)输出电压vo

当取α=0.8,β=0.8时,根据文献[11],可求得分数阶Boost变换器工作于临界状态时的负载电阻值为R=1671.687 Ω,则当R ＜ 1671.687 Ω时,可保证系统工作于伪连续模式.因此,选取R=50 Ω.当PCCM Boost变换器处于稳定运行状态时,其电路模型的电感电流iL和输出电压vo的波形分别如图6(a)和(b)所示.显然,此种情况下Boost变换器工作于电感电流伪连续模式.对其电路模型的电感电流iL和输出电压vo在一个开关周期T内进行平均,并与其数学模型的电感电流iL和输出电压vo进行比较,如图7(a)和(b)所示.由图7结果可知,对PCCM Boost变换器所建的分数阶数学模型是正确的.根据图6(a)可测量出∆iL=0.842 A,iL−min=6.800 A,iL−max=7.642 A,IL=7.211 A.根据图6(b)可测量出∆vo=3.200 V,vo−min=68.610 V,vo−max=71.810 V,Vo=70.210 V. 根据(10)式、(12)式、(13)式和(14)式可分别计算出∆iL=0.720 A,iL−min=6.840 A,iL−max=7.560 A,IL=7.200 A;根据(10)式、(18)式和(19)式可分别计算出∆vo=2.288 V,vo−min=70.856 V,vo−max=73.144 V,Vo=72.000 V.可知,对数学模型的理论分析和电路模型的仿真结果基本一致,从而表明对工作于伪连续模式下Boost变换器理论分析的正确性.

4.3 整数阶PCCM Boost变换器状态平均模型与电路模型的仿真对比

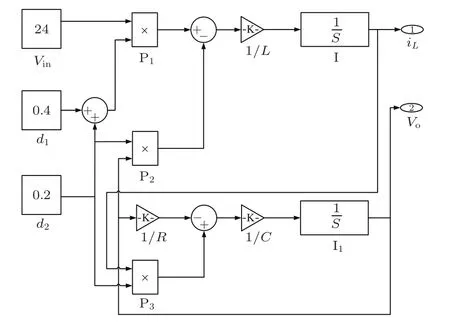
图8 整数阶PCCM Boost变换器Simulink数学仿真模型

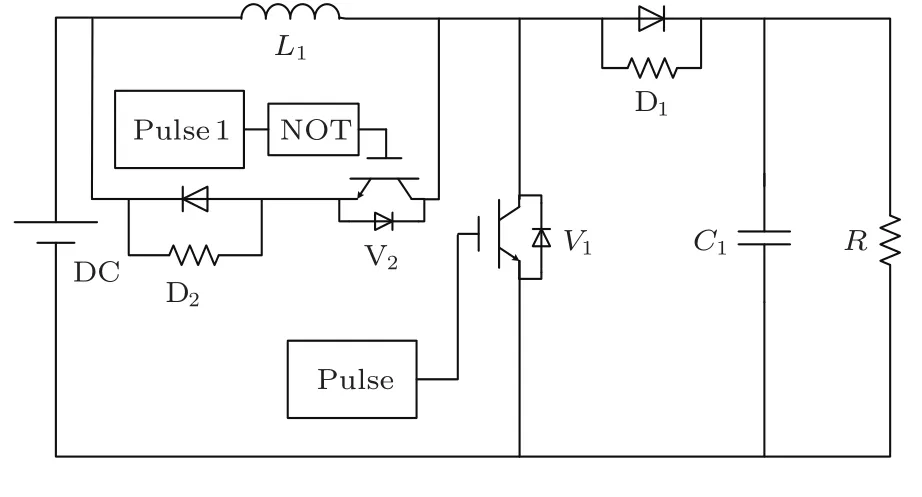
图9 整数阶PCCM Boost变换器Simulink电路仿真模型

当把图4中的分数阶积分单元换为整数阶积分单元时,即采用了整数阶数学模型来描述PCCM Boost变换器,则其整数阶Matlab/Simulink数学仿真模型如图8所示;当用整数阶电感和电容取代图5中的分数阶电感和电容时,则其整数阶电路模型如图9所示,其电路模型的电感电流iL和输出电压vo的波形分别如图10(a)和(b)所示.可见,系统工作于电感电流伪连续模式.对其电路模型的电感电流iL和输出电压vo在一个开关周期T内进行平均,并和其数学模型的电感电流iL和输出电压vo进行比较,如图11(a)和(b)所示.根据图10(a)可测量出∆iL=0.063 A,iL−min=7.092 A,iL−max=7.155 A,IL=7.124 A;根据图10(b)可测量出∆vo=0.230 V,vo−min=70.042 V,vo−max=70.650 V,Vo=70.540 V. 根据(10)式、(12)式、(13)式和(14)式可分别计算出∆iL=0.064 A,iL−min=7.168 A,iL−max=7.232 A,IL=7.200 A;根据(10)式、(18)式和(19)式可分别计算出∆vo=0.240 V,vo−min=71.880 V,vo−max=72.120 V,Vo=72.000 V.

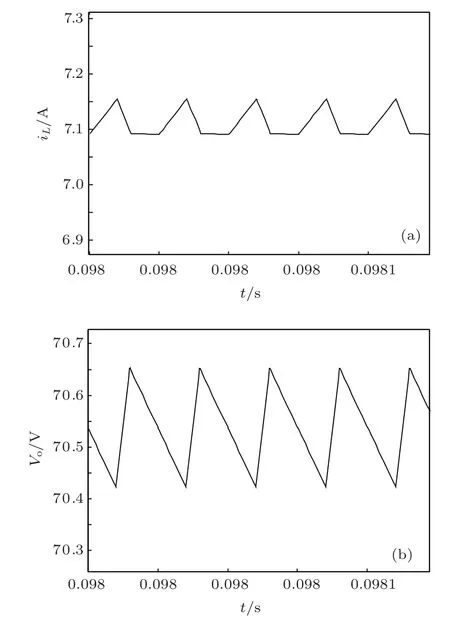
图10 整数阶PCCM Boost变换器电路模型仿真波形(a)电感电流iL;(b)输出电压vo

对比整数阶α=1,β=1和分数阶α=0.8,β=0.8PCCM Boost变换器的数值仿真结果,可知电感电流直流分量IL和输出电压直流分量Vo没有发生变化;而电感电流纹波∆iL、电感电流峰值iL−max和谷值iL−min、输出电压纹波∆vo、输出电压的峰值vo−max和谷值vo−min以及动态响应过程中的上升时间、延迟时间、调节时间、峰值时间、超调量都发生了很大的变化.这就表明用整数阶模型描述本应该用分数阶模型描述的PCCM Boost变换器,将会在电感电流纹波∆iL、电感电流峰值iL−max和谷值iL−min、输出电压纹波∆vo、输出电压的峰值vo−max和谷值vo−min以及动态响应过程中的上升时间、延迟时间、调节时间、峰值时间、超调量等方面得到错误的结果.因此,基于实际电感和电容本质上都是分数阶的事实,为了能够更好的描述工作于电感电流伪连续模式下Boost变换器的动力学特性,须采用其分数阶形式的数学模型.

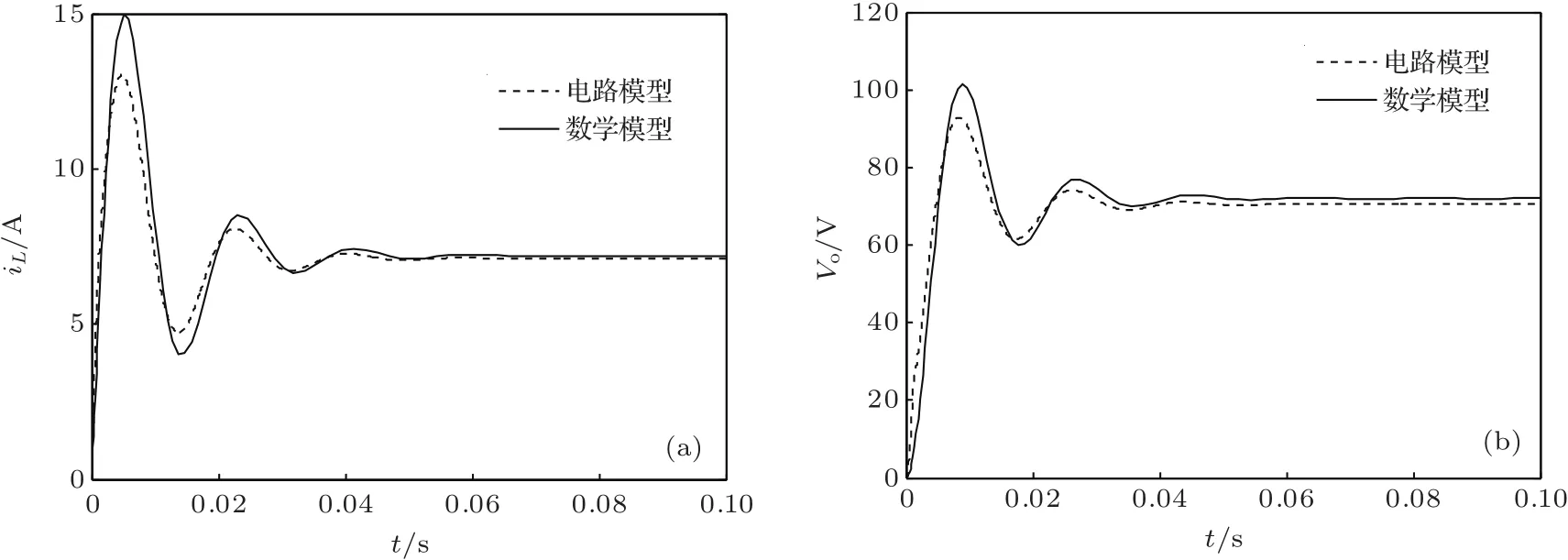
图11 整数阶PCCM Boost变换器电路模型与数学模型仿真波形比较 (a)电感电流iL;(b)输出电压vo

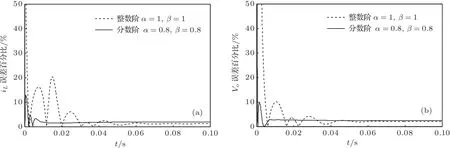
图12 模型误差百分比 (a)电感电流iL;(b)输出电压vo

4.4 模型误差分析

根据(20)式可得模型误差百分比曲线,如图12所示.由文献[19]可知,状态空间平均法仅是平均法的一阶近似,所建的状态空间模型仅能近似的表示电路模型.因此,图12所示的模型误差百分比是合理的,所建立的PCCM Boost变换器的分数阶数学模型是正确的.根据图12可知,模型误差与电感阶数α和电容阶数β有关.因此,须采用分数阶数学模型来描述PCCM Boost变换器的动力学特性.

5 结 论

本文基于分数阶微积分理论,建立了PCCM Boost变换器的分数阶数学模型并进行了相应的理论分析;通过对其数学模型和电路模型的仿真对比,可得出如下结论

1)所建的PCCM Boost变换器的分数阶数学模型可以准确的描述其电路模型.

2)对于分数阶PCCM Boost变换器,所建分数阶数学模型的误差是由于状态平均法只是平均法的近似而产生的,且其模型误差百分比与电感L的分数阶阶数α和电容C的分数阶阶数β有关,即在其他参数不变的情况下,随着电感L的分数阶阶数α和电容C的分数阶阶数β的增大而减小.

3)分数阶PCCM Boost变换器的数学模型形式上虽然和分数阶DCM Boost变换器一样,但由于PCCM Boost变换器不同于DCM Boost变换器的工作特点,使得DCM Boost变换器分数阶模型得出的结论并不能直接应用于PCCM Boost变换器的分数阶模型理论分析.

4)分数阶PCCM Boost变换器的数学模型形式上虽然和分数阶CCM Boost变换器不一样,但通过理论分析及仿真验证,可知CCM Boost变换器分数阶模型得出的结论能够直接应用于PCCM Boost变换器的分数阶模型理论分析.

5)对于分数阶PCCM Boost变换器,在其他参数不变的情况下,其动态响应过程随着电感L的分数阶阶数α和电容C的分数阶阶数β的增大而增大,即其阶跃响应的上升时间、延迟时间、调节时间、峰值时间、超调量都将增大.

综上所述,基于电感和电容本质上是分数阶的事实,本文所建的PCCM Boost变换器的分数阶数学模型是正确的,能够真实的反映PCCM Boost变换器的动力学特性.

[1]Yang S P,Zhang R X 2008 Acta Phys.Sin.57 6837(in Chinese)[杨世平,张若洵 2008物理学报 57 6837]

[2]Zhang C F,Gao J F,Xu L 2007 Acta Phys.Sin.56 5124(in Chinese)[张成芬,高金峰,徐磊2007物理学报56 5124]

[3]Li C L,Yu S M,Luo X S 2012 Chin.Phys.B 21 172

[4]Kenneth S M,Bertram R 1993 An Introduction to the Fractional Calculus and Fractiona Differential Equations(New Jersey:John Wiley&Sons)p21

[5]Shockooh A,Suarez L 1999 Journal of Viberation and Control.5 331

[6]Bohannan G W 2002 Proceedings of the 41st IEEE International Conference on Decision and Control,Tutorial Workshop 2:Fractional Calculus Applications in Automatic Control and Robotics Las Vegas,USA,December 10–13,2002 p1

[7]Westerlund S,Ekstam L 1994 IEEE Trans.Dielectr.Electr.Insulat.1 826

[8]Westerlund S 2002 Dead matter has memory(Kalmar,Sweden:Causal Consulting)chapt.7

[9]Ahmad W 2003 Proceedings of the 2003 International Symposium on Circuits and Systems Bangkok,Thailand,May 25–28,2003 3 p5

[10]Martinez R,Bolea Y,Grau A,Martinez H 2009 IEEE Conference on Emerging Technologies&Factory Automation Palma de Mallorca,Spain,September 22–25,2009 p1

[11]Wang F Q,Ma X K 2011 Acta Phys.Sin.60 070506(in Chinese)[王发强,马西奎 2011物理学报 60 070506]

[12]Wang F Q,Ma X K 2013 Scientia Sinica Technological.43 368(in Chinese)[王发强,马西奎 2013中国科学:43 368]

[13]Ma D S,Ki W H 2007 IEEE Trans.Circuit and Systtems II:Express Briefs.54 825

[14]Kanakasabai V,Ramesh O,Dipti S 2002 IEEE Trans.Power Electronics.17 677

[15]Podlubny I 1999 Fractional differential equations(New York:Academic Press)chapt 1–2,4

[16]Yu H K 2010 M.S.Thesis.(Sichuan:Southeast Jiaotong University)(in Chinese)[于海坤2010硕士学位论文(四川:西南交通大学)]

[17]Wang F Q,Ma X K 2013 Chin.Phys.B 22 236

[18]Xue D Y,Chen Y Q 2007 MATLAB Solutions to Mathematical Problems in Control(Beijing:Tsinghua University Press)p435(in Chinese)[薛定宇,陈阳泉2007控制数学问题的MATLAB求解(北京:清华大学出版社)第435页]

[19]Cao W S,Yang Y X 2007 Journal of System Simulation.19 1329(in Chinese)[曹文思,杨育霞2007系统仿真学报19 1329]