基于跟驰模型的列车运行优化控制模拟研究∗

叶晶晶 李克平 金新民

1)(北京交通大学电气工程学院,北京 100044)

2)(北京交通大学轨道交通控制与安全国家重点实验室,北京 100044)

3)(北京交通大学城市轨道交通北京实验室,北京 100044)

1 引 言

城市轨道交通以运量大,速度快,安全,准点以及污染小等特点,使其成为城市公共交通系统的重要组成部分,受到世界各国的高度重视和广泛关注.发展轨道交通成为解决城市交通拥堵的主要途径之一.列车的运行在整个城市轨道交通系统控制中占据重要地位,优化列车运行不仅可以减少能耗,还能增加乘客的舒适性和确保列车运行的准时性等等.在过去的几十年中,为完成这些优化目标,大量的理论方法和技术策略被提出,例如,利用再生制动能量[1],使用直流电机[2]和使用优化控制策略[3]等等.然而,随着城市轨道交通的快速发展,列车运行速度持续的提高,列车运行控制系统变得越来越复杂.这些因素的存在,给优化列车运行的控制带来了很大的困难,这些问题一直没有得到很好的解决.

实践中,优化列车运行可以通过控制列车运行的速度曲线来实现,这是一种基本的方法.其中关键是如何优化列车运行速度,并且确保列车能按时刻表运行.理论上,有两种方法对这类型问题进行求解:一种是数学建模方法;二是模拟仿真方法[4−10].由于列车运行环境的复杂性,实践中,更倾向于模拟仿真的分析方法.模拟仿真虽然不能求出精确的数值解,但它不存在计算问题.在计算机的帮助下,模拟仿真能够解决许多实际问题,进而受到越来越多的重视.

跟驰模型是一种重要的交通模拟模型,其特点是能够考虑现实中司机的驾驶行为和车辆运行的详细特征.不论是早期的跟驰模型[11−13]还是后来改进的跟驰模型[14−17],对于不同的复杂环境,跟驰模型能够描述出车辆运行的一些主要特征.在交通流理论中,跟驰模型受到越来越多的关注,被广泛用来研究和讨论在不同情况下交通流的演化[18,19].

至今为止,大多数跟驰模型的研究都集中在分析和讨论道路交通问题上,很少用来研究轨道交通,实证研究更是少见.事实上,跟驰模型更适合于模拟轨道交通.因为,在城市轨道交通中,车辆间的作用是单向的,每个驾驶员仅对来自前方车辆的激励作用做出反应,这些都符合跟驰模型的假设条件.因此,本文中,我们应用跟驰模型研究列车运行的优化控制,并以此开展实证研究,其中如何优化列车运行速度是关键.

2 跟驰模型的基本原理

经典的跟驰模型中,第n辆车的速度受到它前面的第n+1辆车的影响.当前车速度发生改变,后车速度也将随之改变,最终使得前后车的速度保持一致.相应车辆的运行动态方程可写为

其中,vn(t)是第n辆车在t时刻的速度,而τ是描述司机的敏感系数.

众所周知,对于连续的两辆车,后车的加减速是由它与前车之间的距离决定的,而为了避免碰撞,必须保持前后两车之间的距离不小于一定的值.从方程(1)出发,Pipes推导出一种新的方程[11]

其中,∆xsafe是安全距离.根据方程(2),前车与后车之间的距离越大,后车的速度也越大.

考虑到更多的实际原因,Newell提出了一种改进的优化速度跟驰模型[13]

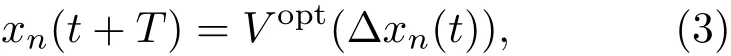
其中,Vopt是优化速度函数,Vopt=(∆xn(t))=v0{1−exp[−(∆xn−∆xsafe)/(v0TS)]},v0是期望的速度,TS是安全时间间隔的特征参数,T是仿真时间步长.

1995年,Bando等提出了著名的优化速度跟驰模型[14]

其中,Vopt是一个以距离∆xn为自变量的函数.通常情况下,当∆xn→ 0,Vopt(∆xn(t))→ 0,而∆xn→ ∞,Vopt(∆xn(t))=vmax,vmax是列车运行中的最大限制速度.方程(4)以第n辆车的位置作为输入量,建立一个二阶微分方程.根据方程(4)中的驾驶规则,第n辆车通过车间距的大小维持安全速度.

3 所提出的模型

城市轨道交通系统中,列车运行通常分为三个阶段:启动,运行和减速制动.列车运行的优化控制主要是通过控制列车运行的速度曲线,在确保列车准时到站的前提下,或是减少列车运行时能量的消耗,或是提高列车运行的稳定性,或是两者兼而有之,本文的研究以节约列车运行的能量消耗为目标.

在不考虑坡道和弯道的情况下,列车运行最理想的节能运行方式是以合理的速度匀速运行.这是因为当列车匀速运行时需要克服的基本阻力最小.为了使匀速运行的区间最长,列车在加速时使用最大加速度,缩短加速需要的距离,而在制动过程中,使用最大的减速度,缩短制动距离.图1显示了列车运行优化速度曲线的基本原理,也是本文研究的理论基础.

图1 列车运行的速度曲线

在经典跟驰模型的基础上,我们改进了优化速度的期望函数,也就是方程(4)中Vopt的表达式.为了实现列车运行节能的要求,根据图1的基本原理,Vopt的表达式需要满足两个条件:1)在列车的加速和减速期间,以最大的加减速率完成加速和减速;2)当列车加速达最大限制速度后以及在进站开始减速前的区间列车均以匀速行驶.根据这两个条件和速度限制,我们提出了一种新的优化速度函数Vopt为

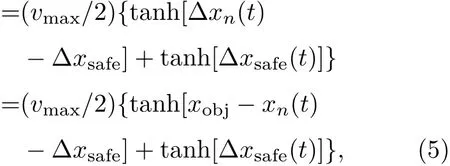
式中,xobj为第n辆列车前方的目标位置,它可能是前方第n+1辆车的位置,也可能是本次列车前方的站点位置,或是前方限速区段分界点的位置.为此,需要对不同的运行条件进行分别处理:1)当目标位置为前车位置时,列车的优化速度由(5)式给出.2)如果目标位置是前方的站点时,优化速度的公式则变形为下面的公式:

其中,abr是列车最大减速率.3)当列车在两个站点间运行时,要受到区间最大速度的限制.列车所受到速度限制可能不止一个,在此情况下,列车运行的速度限制是分区间设置的.假设两个站点间有三个分区限速:1)在启动区间,存在v1max的限制;2)在匀速运行期间,存在v2max的限制;3)在制动区间,存在v3max的限制.其中v1max＜v2max,v3max＜v2max.当列车作减速运行时,从第i个限速区间到第j个限速区间(vjmax＜vimax),优化速度函数则变为

本文中的模型是在开放边界条件下建立的.对于长度为L的仿真系统,边界条件如下:假设列车的发车时间间隔为Tg,当上一辆车离开起点站的时间间隔为Tg时,将有一辆车立刻从起点站出发,新发车的列车立刻按照所提出的模型运行.当列车到达位置L时,列车仅仅只是简单的驶出仿真系统.为了比较仿真结果和实测结果,我们设置仿真的步长为1 m,跟驰模型迭代大约对应1 s,这就是说,实际中的速度v=36 km/h对应于仿真系统中v=10.

4 数值计算

以北京地铁亦庄线为例,应用本文提出的模型进行模拟研究[20].模型中的一些参数设置如下:列车最大加速度abr=1.5 m/s2,最大减速度abr=1.0 m/s2,模拟时间总长为T=3600.发车时间间隔Tg=180.在所模拟的仿真系统中,采用移动闭塞信号控制系统,后车与前车之间仅需要保持一定的安全距离.距离的保持通过控制后车的运行速度来实现.图2显示北京地铁亦庄线的站点分布情况.

北京地铁亦庄线全程总长为22772 m.宋家庄是起点站,列车停留30 s等待乘客上车,亦庄站为终点站,列车停留30 s等待全部乘客下车,而在其他站列车停留等待乘客上下车,停留时间分别显示在表1中.列车在运行过程中,各区段的速度限制如表2所示.

图3显示列车运行过程中时空图的变化(τ=10).图中横坐标表示轨道的位置,纵坐标则表示时间,黑点表示在不同时间各辆列车所处的位置.从图中可以很清楚地看到列车运行过程安全有序,列车间不仅能够始终保持一定的安全距离,而且车流演化很好地保持一致.所有的列车从起点出发,到达前方站点后,按规定的时间停留,直到离开所模拟的系统.从图3中可以看出,在整个运行区间,车流随时间演化较为平稳,列车运行轨迹没有显著的振荡.换句话说,列车的运行过程不但能够节能而且还增加了乘客的舒适性.由此说明所提出模型能够合理地描述城市轨道交通系统中列车运行的一些基本特征.

图2 北京地铁亦庄线站点分布

表1 亦庄线站点停留时间

表2 亦庄线区间最大限制速度

图3 列车运行时空图

列车间保持精确的安全距离是列车运行安全的一个最重要的特征,也是城市轨道交通安全运行的根本保证.图4显示了t=400时最新从起点站出发的列车在整个运行过程中与前车的距离变化(τ=8).图中实线表示的是模拟中计算出的车间距,而虚线则表示列车在速度为20时需要维持的最小安全距离ssafe,ssafe=v2/2abr+sm,其中v=20,sm=10.从图中可以看到,模拟的车间距远远大于最小安全距离,证明所提出的模型是安全的,非常可靠.并在高峰期可以进一步缩短发车时间间隔,以缓解交通压力.

根据图1中描述的列车节能运行的基本原理,我们进一步追踪单个列车在运行过程中位置和速度的变化.图5中黑点表示测量得到的结果,其中水平的实线表示各区间的限速.图中追踪列车t=400最新从起点出发的列车.从图5中可以清楚的看到,在每个区间,列车的运行都经过下列过程:出站加速,然后以最大速度匀速运行,再减速,最后刹车直至进站.由此说明,列车在运行过程中,能够很好地按照优化的速度曲线运行,出站以最大加速度加速,减速也是按最大减速度减速,使得列车在站点间以匀速方式运行的距离最长,从而最大化地实现列车运行过程中的能量节约.另一方面,列车在各区间能够始终保持限速运行,同时也证明了所提出模型的有效性和可靠性.

图4 t=400出发的列车与前车之间的距离

为了进一步验证所提出模型的有效性,我们比较了模拟过程中列车各站之间的运行时间和实际列车的运行时间,图6是比较的结果.在图6中,实线表示模拟运行时间,而虚线则是实际运行时间.从图6中可以得到这样的结论:两条曲线在形状很相似,幅值上仿真数据比实际数据小,但相差不大.模拟系统中,列车在亦庄线上运行的总的时间为1840 s,而实际上列车真正的运行时间为2005 s.这表示模拟结果和实际运行时间很接近.而存在的偏差的原因是,在我们的模拟系统中,设定列车一直在平直轨道上运行,没有考虑坡道和弯道等因素,而实际轨道线路并非如此,北京地铁亦庄线许多区段存在一定弯道和坡道,而坡道和弯道的存在会使列车进一步降低它的运行速度,导致模拟运行时间和实际运行时间不一致.

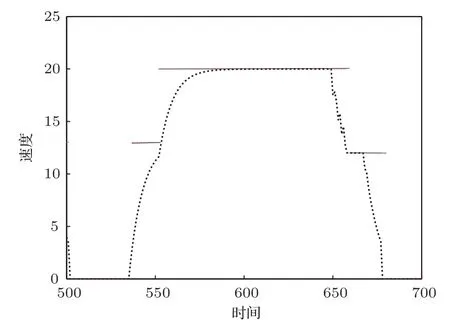
图5 列车运行速度图

图6 模拟运行时间与实际运行时间比较

5 结 论

本文中,根据城市轨道交通中列车运行的一些基本特性,我们提出了一种改进的优化速度跟驰模型,并且应用所提出的模型模拟北京地铁亦庄线列车运行过程.通过数值模拟,分析和讨论了列车运行时空图中列车流演化的特点,更进一步的分析了列车位置,速度和时间的关系.模拟结果说明了我们所提出的模型不仅能很好的描述列车运行的主要特征,而且也能实现列车运行的优化控制.比较模拟测量得到的结果和实际数据,证明所提出模型是有效的,能合理地刻画城市轨道交通列车运行的特征.

我们认为所提出的模型为获得城市轨道交通系统列车运行的优化速度曲线提供了一个好的方法,也为研究城市轨道交通系统的其他问题给出了一种基本模型,例如,研究地铁列车运行过程中的再生制动.进一步研究,可以面向复杂的交通环境开展探索,例如,考虑列车运行过程中的弯道和坡道等,这也是我们的后续所要开展的研究工作.

[1]Adinol fiA,Lamedica R,Modesto C 1998 IEEE Transactions on Power Delivery 13 1536

[2]Kokotovic P,Singh G 1972 IEEE Transactions on Automatic Control 17 92

[3]Hwang H S 1998 IEEE Transactions on Systems,Man,and Cybernetics A:Systems and Humans 28 791

[4]Duarte M A,Sotomayor P X 1999 Optimal Control Applications and Methods 20 283

[5]Howlett P 1996 Automation 3 519

[6]Liu R Golovitcher I M 2003 Transportation Research Part A:Policy and Practice 37 917

[7]Howlett P G 2000 Annals of Operation Research 98 1257

[8]Li K P,Gao Z Y,Mao B H 2007 Chin.Phys.B 16 359

[9]Chang C S,Sim S S 1997 Proceedings-Electric Power Applications 144 65

[10]Cheng J X,Howlett P G 1993 IEEE Transactions Automatic Control 38 1730

[11]Pipes L A 1953 J.Appl.Phys 24 274

[12]Chandler R E,Herman R,Montroll E W 1958 Operational Research 6 165

[13]Newell G F in 1961 Operational Research 9 209

[14]Bando M,Hasebe K,Nakayama A 1995 Phys.Rev.E 51 1035

[15]Helbing D,Tilch B 1998 Phys.Rev.E 58 133

[16]Treiber M,Hennecke A,Helbing D 2000 Phys.Rev.E 62 1805

[17]Tomer E,Safonov L,Havlin S 2000 Phys.Rev.Lett.84 382

[18]Tang T Q,Huang H J,Shang H Y 2010 Acta Phys.Sin.59 6003(in Chinese)[唐铁桥,黄海军,尚华艳 2010物理学报59 6003]

[19]Yuan N,Hua C C 2012 Acta Phys.Sin.61 160509(in Chinese)[袁娜,化存才 2012物理学报 61 160509]

[20]Su S,Li X,Tang T,Gao Z Y 2013 IEEE transaction on intelligent transportation system 14 883