乘性和加性α稳定噪声环境下的过阻尼单稳随机共振现象∗

焦尚彬 任超 李鹏华 张青 谢国

(西安理工大学自动化与信息工程学院,西安 710048)

1 引 言

传统的微弱信号检测方法大多都是通过抑制噪声来实现微弱信号检测的,而随机共振(stochastic resonance,SR)噪声增强的反常机理为微弱信号的检测开辟了新的思路.SR最早被发现存在于非线性双稳态系统中,随着研究的不断深入,1993年Stocks等[1]首次发现了欠阻尼单稳态系统的SR现象,随后单稳SR现象受到了学者们的关注,并取得了相应的进展[2−11].康等[12]研究了单模非线性光学系统中的单稳SR现象,并对单稳系统发生SR的一般条件给予了分析,认为无论在多稳或单稳情形下,SR现象都会发生.Guo等[13,14]研究了乘性和加性高斯噪声共同作用下的单稳SR现象,通过分析发现加入乘性噪声后可将单稳系统等效为双稳系统进行研究.

综观已有的单稳SR研究成果,其基本上都是假设在高斯噪声的条件下取得的.α稳定分布是一种能够保持自然噪声过程的产生机理和传播条件的极限分布,它能够非常好地与实际数据相符合,高斯分布只是它的一个特例[15],故用α稳定分布描述的α稳定噪声要比高斯噪声更具有代表性,近几年来α稳定噪声环境下的双稳SR现象受到了学者们的广泛关注,并且取得了很大的进展[16−21].而α稳定噪声环境下的单稳SR现象的相关研究只是刚刚起步.Dybiec[22]研究了受周期性调制Lévy噪声扰动的四阶单势阱系统的SR现象.相对于双稳系统而言,单稳系统具有系统参数少、结构简单等优点,故对其进行研究是十分有意义的.在实际中,待检测信号频率可能不止一个,并且可能是高频信号,这就超出了SR理论所要求的频率范围[23].因此,需要对多个低频、高频微弱信号的检测问题展开研究.然而到目前为止,有关α稳定噪声环境下多频微弱信号检测的单稳SR现象的研究尚未见相关报道.

文献[24]已对α稳定噪声环境下的多频双稳SR现象进行了研究,所得结论可为实现α稳定噪声环境下双稳SR系统参数的自适应调节奠定基础.本文在文献[24]的研究基础上,对α稳定噪声环境下的多频单稳SR现象进行了研究,主要研究内容包括以下几个方面:本文在对称和非对称、乘性和加性α稳定噪声环境下,先对多个低频微弱信号激励的单稳SR现象进行研究,随后结合参数补偿的方法对多个高频微弱信号激励的单稳SR现象进行研究,探究α稳定噪声特征指数α(0＜α≤2)、对称参数β(−1≤β≤1),单稳系统参数a及乘性α稳定噪声放大系数D对共振输出效应的作用规律.针对α稳定噪声环境下的单稳SR现象,得出了与文献[24]所研究的双稳SR现象不一样的结论.

2 模型与方法

由于α稳定分布模型(即特征函数)及α稳定噪声的产生方法(Janicki-Weron算法,JW算法)已在文献[24—26]中有了详细的说明,故本文中不再赘述.由α稳定分布的特征函数可知,α稳定噪声的分布特征是由特征指数α∈(0,2]、对称参数β∈[−1,1]、尺度参数σ∈[0,+∞)及位置参数µ∈(−∞,+∞)四个参数来决定的,通常记α稳定分布为Sα(σ,β,µ).

2.1 单稳SR系统模型

单稳SR系统有多种模型[2−5,13,27],本文仅考虑其中一种典型模型所描述的α稳定噪声环境下的过阻尼单稳SR系统,其模型如下:

式中,U(x)为非线性单稳态势函数,U(x)=(a/4)x4,a为系统参数,且a＞ 0;ηα(t)为加性α稳定噪声,代表外噪声;s(t)为输入信号,在本文中为多频叠加信号,如下式所示:

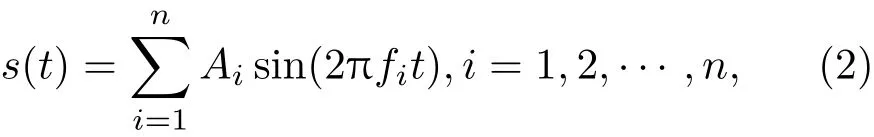
式中,Ai为第i路信号幅值,fi为第i路信号频率,n表示输入信号的数量.

过阻尼单稳SR系统因其势函数为单势阱而得名,但随着乘性噪声的加入,其可以形成势垒,产生两个势阱,进而可以等效为双稳SR系统来研究.由于乘性噪声是随机变化的,故所形成势垒的高度也就是一个随机量,这与双稳SR系统是有所区别的.受乘性和加性α稳定噪声驱动的过阻尼单稳SR系统可用如下的朗之万(Langevin)方程[6,13]进行描述:

式中,ξα(t)为乘性α稳定噪声,代表信号在传输过程中信道内部依附于信号而存在的内噪声,其噪声分布参数设置与ηα(t)相同;D代表ξα(t)的放大系数,通过改变D可以间接地改变ξα(t)的强度;其余参数含义不变.

本文采用四阶龙格-库塔(Runge-Kutta)算法对(3)式进行求解,具体解法见文献[18,21,24].由于特征指数α越小,α稳定分布的脉冲性就越强,这就导致粒子在长时间跳跃过程中路径变化很快以至无限大,因此,在数值模拟中需要对输出信号 x(t)进行人为的截断[19,21,28],来解决粒子跳跃轨迹无限大的问题,文中所采取的截断措施为:当|x(t)|＞ 5时,令x(t)=sign(x(t))×5.

2.2 信噪比增益及平均信噪比增益

信噪比增益是衡量SR系统对输入信号增强和改善作用的重要指标,只有当信噪比增益大于1时,才能说明SR系统对信号具有明显的增强和改善作用[23,29],并且信噪比增益越大检测效果越好.假设输入信号为(2)式所示多频信号,第 i路信号的信噪比增益记为Gi,则其定义如下:

式中,SP(ωi)in和SP(ωi)out分别表示SR前后第i路信号的功率,NP(ωi)in和NP(ωi)out分别表示在第i路输入信号频率处系统的输入输出平均噪声功率.

为了衡量SR系统对多个频率信号的整体检测效果,利用平均信噪比增益对SR系统输出效应进行衡量.平均信噪比增益记为MG,其定义如下:

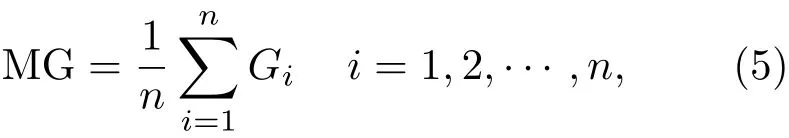
式中各参数含义不变.

2.3 参数补偿SR

目前,处理高频微弱信号的方法有二次采样[30−32]、调制[33]以及参数补偿[24,34,35]等. 与二次采样、调制等方法相比,参数补偿法不受采样频率以及要求待检测信号频率已知等因素的影响,只需知道待检测信号频率所处的大致频段即可,从而提高了高频微弱信号检测的灵活性,因此本文采用参数补偿的方法来实现高频微弱信号的SR检测,其原理如下:

假设输入信号s(t)=Asin(2πft),则(3)式变为

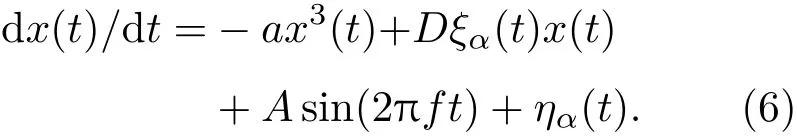
对(6)式左右两边同时对 t进行积分可得系统输出为

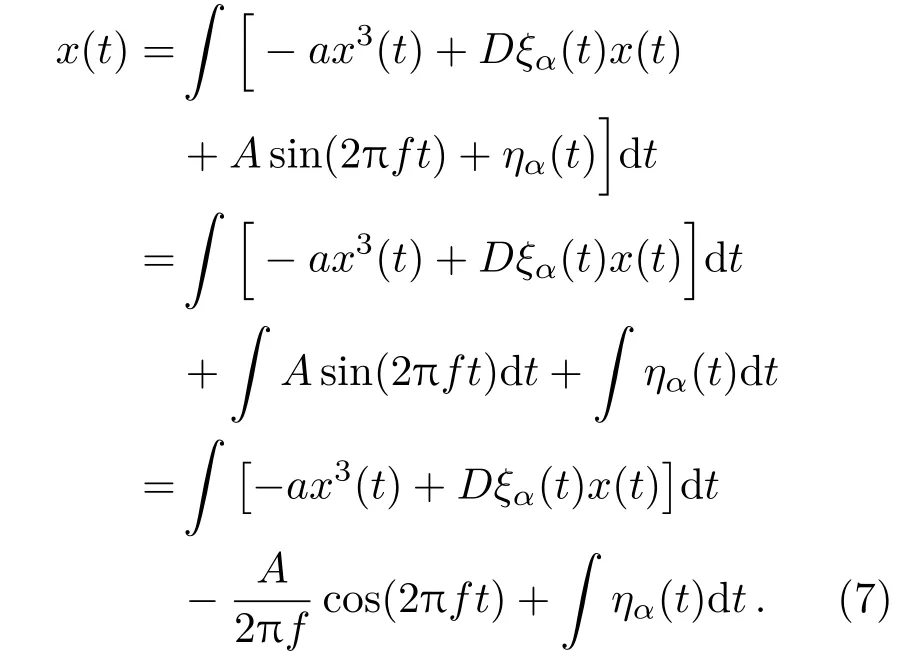
从(7)式右边第二项可以看出,输入信号s(t)在经过单稳系统时,其幅值会被积分环节(阻尼项)缩减为原信号的1/2πf,输入信号的频率越高,被缩减的程度就越大,这样高频信号即使经过单稳系统的处理,输出信号中也无法发现高频信号的存在.因此,可以在Langevin方程中加入一个放大环节来抵消阻尼项的影响.加入放大环节后的Langevin方程变为

式中,K为补偿参数,理论上K的取值要与2πf相当,但在仿真实验中,为了取得相对较好的检测效果,K的取值一般要大于2πf;其余参数含义不变.

3 α稳定噪声环境下的多频微弱信号检测及单稳SR现象

根据SR的相关理论可知,势垒的高低直接影响着SR系统的输出效应.势垒高度越高,就要求输入信号和噪声具有较多的能量才能产生SR现象;反之,产生SR现象所要求的输入信号和噪声能量就越小.根据双稳系统势垒高度的定义式[23]可得乘性α稳定噪声作用下单稳系统势垒高度的表达式为

从式中可以看出势垒高度是由系统参数a、α稳定噪声分布参数(α,β,σ,µ)及乘性α稳定噪声放大系数D共同决定的,因此,本文将在α和β分别取不同值时,研究在一定范围内通过调节a或D来实现高、低频(均为多频)微弱信号检测的SR现象,探究不同α,β,a和D对系统共振输出效应的作用规律.需要说明的是,文中所给出的MG随a和D的演变规律曲线均是取20次实验的平均值绘制而成的.

3.1 低频(多频)微弱信号检测的单稳SR现象

在研究低频(多频)微弱信号检测的单稳SR现象时,仿真实验中所选取的淹没在α稳定噪声中的输入信号为

式中,A1=A2=A3=0.8,f1=0.01 Hz,f2=0.03 Hz,f3=0.05 Hz.另外,令α稳定噪声服从S1(1,0,0),a=0.1,D=0.374,采样频率为fs=7.306 Hz.仿真实验,结果如图1所示.

图1(a)为输入信号与α稳定噪声混合信号的时域图,图1(b)为图1(a)的局部放大图.从图1(a)和(b)中可以看出,输入信号完全被α稳定噪声所淹没,无法从时域图中得到输入信号的时域信息.对上述混合信号进行快速傅里叶变换(FFT)得到其功率谱如图1(c)所示,从该图中也无法得到输入信号的频率信息.将该混合信号作为输入信号送入单稳SR系统,然后调节a和D,当a=0.1和D=0.374时,SR系统输出功率谱如图1(d)所示,从图中可以清晰地看出,在频率0.01 Hz,0.03 Hz及0.05 Hz处出现了三个明显的尖峰,这三个尖峰所对应的频率恰恰就是混合信号中三个输入信号的频率.说明通过改变a和D有效地调节了势垒高度使粒子有足够的能量越过势垒,在加入乘性α稳定噪声后的单稳系统的两个势阱间周期性的跳跃,即达到了SR状态,实现了α稳定噪声环境下多个低频微弱信号的单稳SR检测.

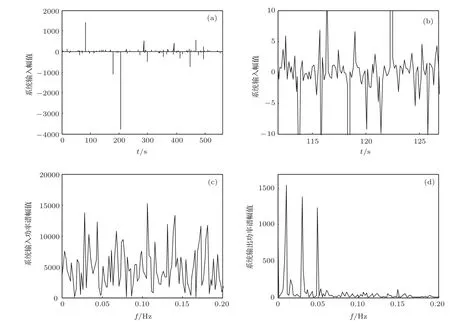
图1 (a)系统输入时域图;(b)系统输入时域图的局部放大图;(c)系统输入功率谱图;(d)系统输出功率谱图(多个低频信号)

为了明确多个低频微弱信号检测时α,β,a及D与单稳系统的共振输出效应之间的关系,展开如下仿真实验研究.

3.1.1 不同特征指数α下的低频单稳SR

令α分别为0.5,0.8,1,1.2和1.5,其余噪声分布参数分别为β=0,σ=1,µ=0,s(t)和fs不变.固定D=0.374,仿真实验得到MG随a的演变规律曲线如图2所示.固定a=0.1,仿真实验得到MG随D的演变规律曲线如图3所示.

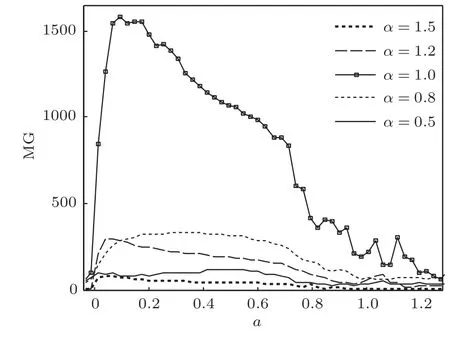
图2 不同α作用下MG随a的演变规律曲线(低频)

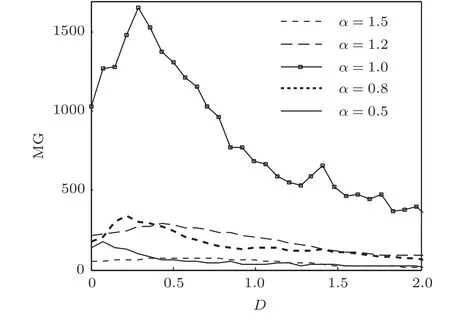
图3 不同α作用下MG随D的演变规律曲线(低频)

从图2中可以看出,当α取不同值时,MG随a均是非线性变化的,且对于每一个α,MG都存在一个最大值,说明对于a而言,存在一个最优值可使系统产生最佳的SR效应.通过对α=1时MG随a的演变规律曲线分析发现,当a从零开始逐渐增大到0.1的过程中,势垒高度在不断的降低,此时粒子发生跃迁所需的能量也在逐渐减少,即粒子逐渐变得更容易发生跃迁,因此,MG随着a的增大呈上升趋势;当a=0.1时,输入信号、噪声及非线性系统三者之间达到了最佳的匹配关系,系统产生了最佳的SR效应,MG也达到了最大值;当a从0.1开始继续增大时,势垒高度仍在不断的降低,以至于使加入乘性α稳定噪声的单稳系统的双势阱又逐渐变成了单势阱,此过程中,粒子也将从在双势阱中的周期性跃迁逐渐变为单势阱内的小幅波动,SR现象随之逐渐消失,故MG随着a的继续增大呈逐渐下降的趋势.从图3中也可以看出,当α取不同值时,MG随D也是非线性变化的,且对于每一个α,MG都存在一个最大值,说明对于D而言,也存在一个最优值可使系统产生最佳的SR效应.通过对α=1时MG随D的演变规律曲线分析发现,当D从零开始逐渐增大到0.374的过程中,随着乘性α稳定噪声的加入,单稳系统的势函数逐渐由单势阱变成了双势阱,粒子也将从在单势阱内的小幅波动逐渐变为双势阱中的周期性跃迁,SR现象随之逐渐产生,故MG随着D的增大呈逐渐上升的趋势;当D=0.374时,输入信号、噪声及非线性系统三者之间达到了最佳的匹配关系,系统产生了最佳的SR效应,MG也达到了最大值;当D从0.374开始继续增大时,势垒高度在不断的增加,输入信号和噪声所提供的能量逐渐不足以使粒子在两个势阱间周期性的跃迁,SR现象随之逐渐消失,故MG随着D的继续增大呈逐渐下降的趋势.当α分别为0.5,0.8,1.2和1.5时,MG随a或D的演变规律曲线所呈现出的非线性特征及其机理与α=1时的情形是相同的.另外还发现,当α取不同值时,共振效应相对较好的a或D区间基本都集中在同一个区域;当α＞1时,随着α的增大,单稳系统的共振输出效应呈逐渐递减的趋势,当α＜1时,随着α的减小,单稳系统的共振输出效应呈逐渐递减的趋势.

3.1.2 不同对称参数β下的低频单稳SR

令β分别为−1,0和1,其余噪声分布参数分别为α=1.2,σ=1,µ=0,s(t)和fs不变.固定D=0.374,仿真实验得到MG随a的演变规律曲线如图4所示.固定a=0.1,仿真实验得到MG随D的演变规律曲线如图5所示.

从图4和图5中可以看出,当β取不同值时,MG随a或D均是非线性变化的,且对于每一个β,MG都存在一个最大值,说明对于a或D而言,存在一个最优值可使系统产生最佳的SR效应;当β取不同值时,共振效应相对较好的a或D区间基本都集中在同一个区域;β=0时的MG要高于β≠0时的MG,即α稳定噪声呈对称分布时单稳系统的共振输出效应要好于非对称分布时的情形.

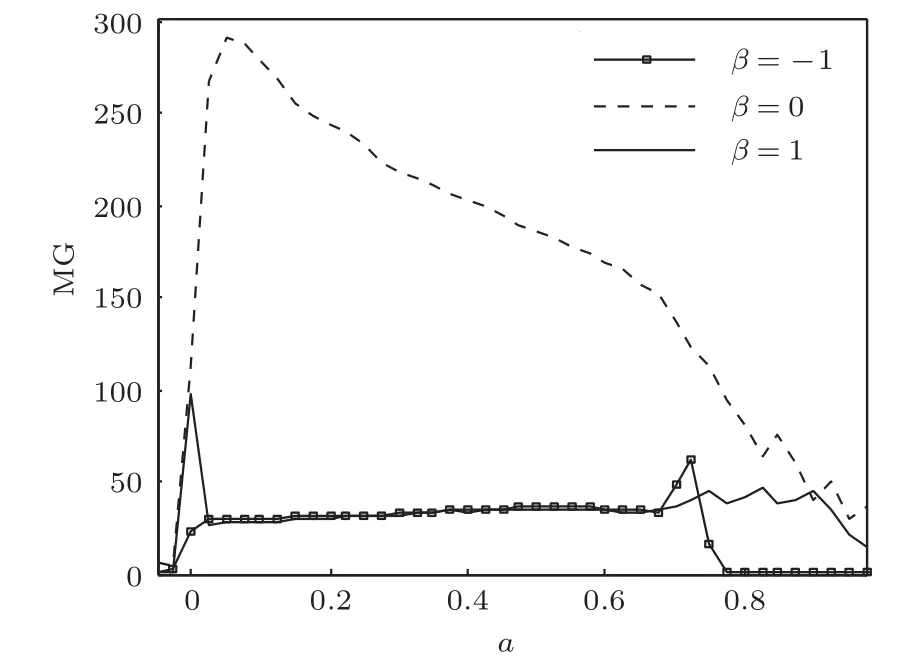
图4 不同β作用下MG随a的演变规律曲线(低频)

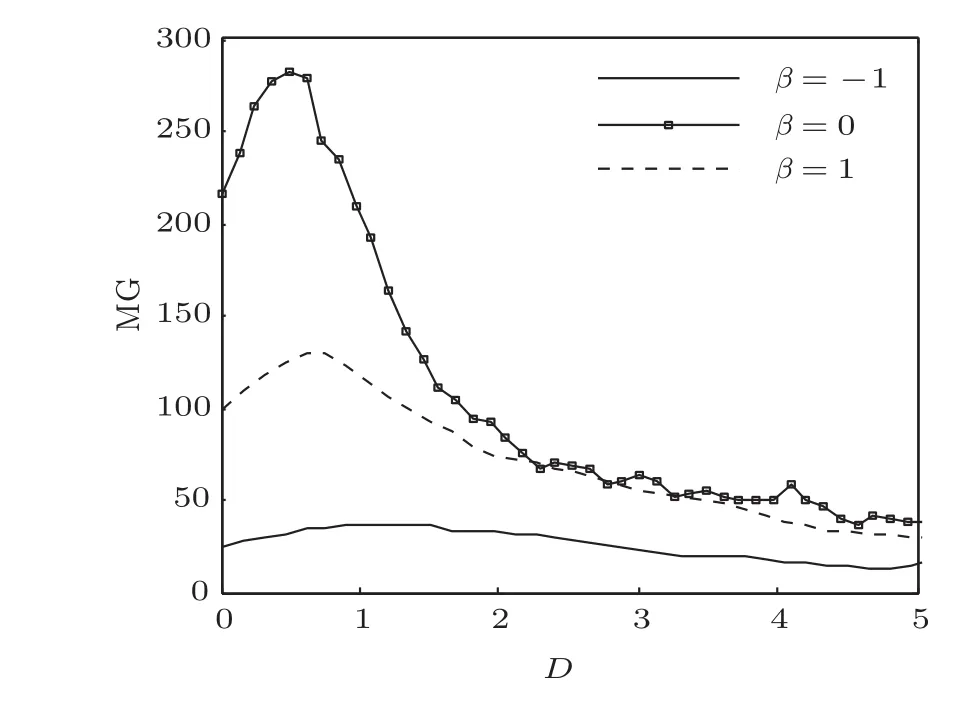
图5 不同β作用下MG随D的演变规律曲线(低频)

3.2 高频(多频)微弱信号检测的单稳SR现象

在研究高频(多频)微弱信号检测的单稳SR现象时,仿真实验所选取的输入信号如(10)式所示,其中A1=A2=A3=1,f1=1000 Hz,f2=2000 Hz,f3=3000 Hz.另外,令α稳定噪声服从S1(1,0,0),a=0.01,D=0.374,fs=204800 Hz,K=100000.仿真实验,结果如图6所示.

图6(a)和(b)分别为输入信号与α稳定噪声混合信号的时域图和功率谱图,从这两幅图中可以看出,输入信号完全被α稳定噪声所淹没,无法得到输入信号的时频域信息.同样,将该混合信号作为输入信号送入单稳SR系统,然后调节a和D,当a=0.01和D=0.374时,SR系统输出功率谱如图6(c)所示,从图中可以清晰地看出,在频率1000 Hz,2000 Hz及3000 Hz处出现了三个明显的尖峰,这三个尖峰所对应的频率恰恰也是混合信号中三个输入信号的频率.说明在实现α稳定噪声环境下多个低频微弱信号的单稳SR检测的基础上,结合参数补偿的方法可进一步实现α稳定噪声环境下多个高频微弱信号的单稳SR检测.

图6 (a)系统输入时域图;(b)系统输入功率谱图;(c)系统输出功率谱图(多个高频信号)

为了明确多个高频微弱信号检测时α,β,a及D与单稳系统的共振输出效应之间的关系,进一步按研究多个低频微弱信号激励的单稳SR现象的方法对不同α或β作用下的多个高频微弱信号激励的单稳SR现象展开了研究,得到了MG与a及MG与D之间的演变规律曲线,分别如图7、图8、图9和图10所示.图7和图8中的小图为大图的局部放大图(大小图中的坐标及线条设置相同),以便更清晰地观察纵坐标接近于零时曲线的变化趋势.

图7 不同α作用下MG随a的演变规律曲线(D=0.374,β=0,高频)

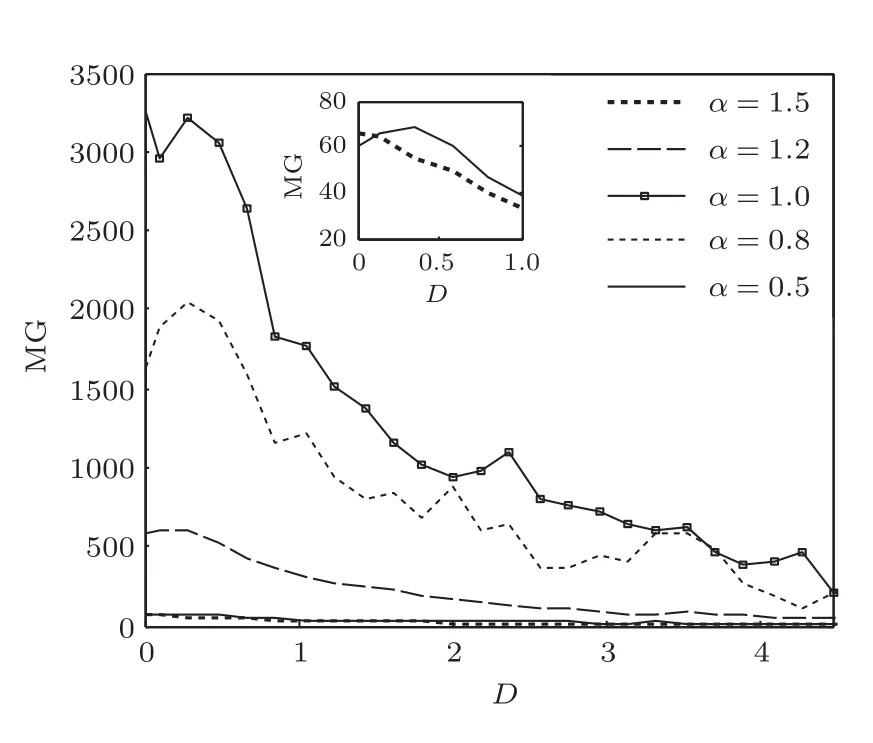
图8 不同α作用下MG随D的演变规律曲线(a=0.01,β=0,高频)

图9 不同β作用下MG随a的演变规律曲线(D=0.374,α=1.2,高频)

图7、图8、图9及图10显示了在不同α或β作用下,多个高频微弱信号激励单稳SR系统时MG随a或D的演变规律曲线.通过分析发现,在进行高、低频(均为多频)微弱信号检测时MG随a或D的演变规律是一致的.

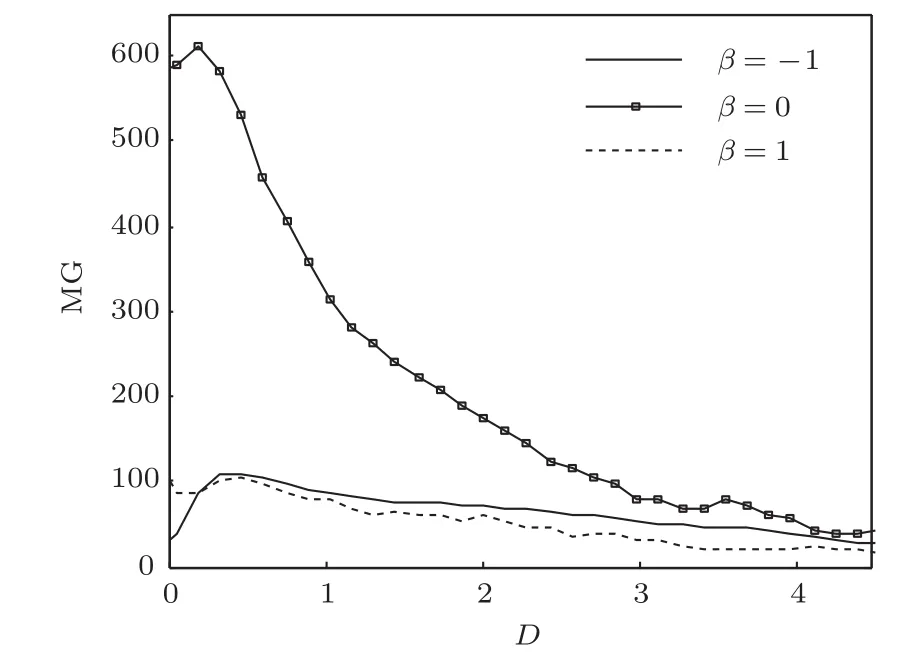
图10 不同β作用下MG随D的演变规律曲线(a=0.01,α=1.2,高频)

通过对上文中MG随a或D演变规律的分析发现,可使单稳系统产生相对较好的SR效应的a或D区间只有一个,而文献[24]中发现有多个系统参数(a或b)区间可使双稳系统产生相对较好的SR效应.

4 α稳定噪声环境下的单频微弱信号检测及单稳SR现象

本文以信噪比增益Gi(此时只有一路信号,故i=1)为α稳定噪声环境下单频单稳SR现象的衡量指标,以研究α稳定噪声环境下多频单稳SR现象的方法对α稳定噪声环境下单频单稳SR现象展开了研究,并得到了相应的实验结果.通过对实验结果进行分析总结发现,在研究α稳定噪声环境下单、多频单稳SR现象时所得结论是一致的.限于篇幅,文中仅给出α稳定噪声环境下单个低频微弱信号的单稳SR检测结果,如图11所示,其他规律曲线不再给出.

图11 单个低频微弱信号检测结果(a)系统输入时域图;(b)系统输入功率谱图;(c)系统输出功率谱图(A=0.8,f=0.02 Hz,α稳定噪声服从S1(1,0,0),a=0.1,D=0.32,fs=9 Hz)

5 结 论

本文将α稳定噪声与单稳随机共振(SR)系统相结合,研究了乘性和加性α稳定噪声环境下单、多频微弱信号激励的单稳SR现象.探究了α稳定噪声分布参数α,β,单稳系统参数a及乘性α稳定噪声放大系数D与单稳系统共振输出效应之间的关系,揭示了α,β,a及D对单稳系统共振输出效应的作用规律.得到如下结论:1)在一定范围内,通过调节a或D均可实现α稳定噪声环境下单个或多个低频微弱信号的单稳SR检测,结合参数补偿的方法,可以进一步实现单个或多个高频微弱信号的单稳SR检测.2)当α或β取不同值时,平均信噪比增益(MG)随a或D均是非线性变化的,且对于每一个α或β,MG都存在一个最大值,即对于a或D而言,存在一个最优值可使系统产生最佳的SR效应.另外,共振效应相对较好的a或D区间基本都集中在同一个区域.3)当α＞1时,单稳系统的共振输出效应随α的增大而减弱;当α＜1时,单稳系统的共振输出效应随α的减小而减弱.4)β=0时的MG要高于β≠0时的值,即α稳定噪声呈对称分布时单稳系统的共振输出效应要好于非对称分布时的情形.5)在高、低频微弱信号检测中,α或β对单稳系统共振输出效应的作用规律是相同的.6)在研究α稳定噪声环境下单、多频单稳SR现象时所得结论是一致的.上述结论将有助于自适应调参单稳SR系统中参数的合理选取,为实现α稳定噪声环境下微弱信号单稳SR检测的实际工程应用奠定基础.

[1]Stocks N G,Stein N D,McClintock P V E 1993 J.Phys.A:Math.Gen.26 L385

[2]Vilar J M G,Rub J M 1996 Phys.Rev.Lett.77 2863

[3]vstigneev M,Reimann P,Pankov V,Prince R H 2004 Europhys.Lett.65 7

[4]Zhang W,Xiang B R 2006 Talanta 70 267

[5]Guo F,Huang Z Q,Fan Y,Li S F,Zhang Y 2009 Chin.Phys.Lett.26 100504

[6]Zhou B C,Xu W 2009 Chaos,Solitons&Fractals 40 401

[7]He C D,Xu W,Yue X L 2010 Acta Phys.Sin.59 5276(in Chinese)[何成娣,徐伟,岳晓乐2010物理学报59 5276]

[8]Zhou Y R 2011 Chin.Phys.B 20 010501

[9]Li J M,Chen X F,He Z J 2011 Journal of Mechanical Engineering 47 58(in Chinese)[李继猛,陈雪峰,何正嘉2011机械工程学报47 58]

[10]Yao M L,Xu W,Ning L J 2012 Nonlinear Dyn.67 329

[11]Zhang X Y,Xu W,Zhou B C 2012 Acta Phys.Sin.61 030501(in Chinese)[张晓燕,徐伟,周丙常 2012物理学报61 030501]

[12]Kang Y M,Xu J X,Xie Y 2003 Acta Phys.Sin.52 2712(in Chinese)[康艳梅,徐健学,谢勇2003物理学报52 2712]

[13]Guo F 2009 Physica A 388 2315

[14]Guo F,Luo X D,Li S F,Zhou Y R 2010 Chin.Phys.B 19 080504

[15]Qiu T S,Zhang X X,Li X B,Sun Y M 2004 Statistical Signal Processing—Non-Gaussian Signal Processing and its Applications(Beijing:Publishing House of Electronics Industry)p140(in Chinese)[邱天爽,张旭秀,李小兵,孙永梅2004统计信号处理—非高斯信号处理及其应用(北京:电子工业出版社)第140页]

[16]Dybiec B,Gudowska-Nowak E 2006 Acta Phys.Pol.B 37 1479

[17]Zeng L Z,Bao R H,Xu B H 2007 J.Phys.A:Math.Theor.40 7175

[18]Zhang W Y,Wang Z L,Zhang W D 2009 Control Engineering of China 16 638(in Chinese)[张文英,王自力,张卫东2009控制工程16 638]

[19]Zeng L Z,Xu B H 2010 Journal of physics A:Statistical Mechanics and its Applications 22 5128

[20]Srokowski T 2012 Eur.Phys.J.B 85 1

[21]Zhang G L,Lü X L,Kang Y M 2012 Acta Phys.Sin.61 040501(in Chinese)[张广丽,吕希路,康艳梅 2012物理学报61 040501]

[22]Dybiec B 2009 Phys.Rev.E 80 041111

[23]Hu N Q 2012 Stochastic Resonance Weak Characteristic Signal Detection Theory and Methods(Beijing:National Defense Industry Press)p60(in Chinese)[胡茑庆2012随机共振微弱特征信号检测理论与方法(北京:国防工业出版社)第60页]

[24]Jiao S B,Ren C,Huang W C,Liang Y M 2013 Acta Phys.Sin.62 210501(in Chinese)[焦尚彬,任超,黄伟超,梁炎明2013物理学报62 210501]

[25]Tang Y,Zou W,Lu J Q,Kurths J 2012 Phys.Rev.E 85 1539

[26]Liang Y J,Chen W 2013 Signal Processing 93 242

[27]Agudov N V,Krichigin A V 2008 Radiophysics and Quantum Electronics 51 812

[28]Weron R 1996 Statist.Prob.Lett.28 165

[29]Wan P,Zhan Y J,Li X C,Wang Y H 2011 Acta Phys.Sin.60 040502(in Chinese)[万频,詹宜巨,李学聪,王永华2011物理学报60 040502]

[30]Leng Y G,Wang T Y 2003 Acta Phys.Sin.52 2432(in Chinese)[冷永刚,王太勇 2003物理学报 52 2432]

[31]Leng Y G,Wang T Y,Qin X D,Li R X,Guo Y 2004 Acta Phys.Sin.53 0717(in Chinese)[冷永刚,王太勇,秦旭达,李瑞欣,郭焱2004物理学报53 0717]

[32]Leng Y G 2009 Acta Phys.Sin.58 5196(in Chinese)[冷永刚2009物理学报58 5196]

[33]Lin M,Huang Y M 2006 Acta Phys.Sin.55 3277(in Chinese)[林敏,黄咏梅 2006物理学报 55 3277]

[34]Jiao S B,He T 2013 Computer Engineering and Applications(in Chinese)[焦尚彬,何童2013计算机工程与应用]

[35]Lü Y,Wang C Y,Tian Y,Hou B 2010 China Academic Journal Electronic Publishing House 8 40(in Chinese)[吕运,王长悦,田野,侯彪 2010机械与电子 8 40]