离散非线性动力系统的倍周期分叉控制

欧阳克俭，唐驾时

（1.国网湖南省电力公司 电力科学研究院，长沙410007；2.湖南大学 工程力学系，长沙410002）

离散非线性动力系统的倍周期分叉控制

欧阳克俭1，唐驾时2

（1.国网湖南省电力公司 电力科学研究院，长沙410007；2.湖南大学 工程力学系，长沙410002）

研究离散非线性系统的倍周期分叉的分叉控制,设计线形控制器，非线性控制器以及状态反馈控制方法控制非线性动力系统。得到在控制前和控制后的分叉图，使系统的分叉达到预期的控制目的。根据实际的应用目的可以设计不同的控制器，其中线性控制器和非线性控制器由粗调和微调两部分组成。可以使系统分叉得到有效控制。选用的状态反馈控制器在适当选择控制器和有效的调控控制参数可以使分叉的效果控制达到良好的效果。

振动与波；倍周期分叉；分叉控制；状态反馈控制；分叉图

1 控制方法

考虑如下逻辑映射

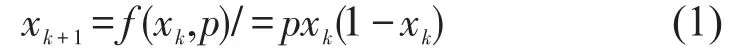
其中p是大于零的实数，x∈[0,1]。这是一个典型的倍周期分叉系统。系统x=(fx,p)得两个平衡点

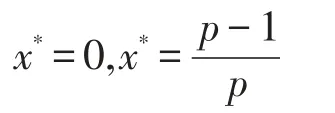
在0＜p＜1时，系统f(x)=px(1-x)离散非线性动力特性相对清晰，不管取什么初值x0，当k→∞，只有x*=0是稳定的；

在1＜p＜3时，不管取什么初值x0时，当k→∞，是稳定的；

在3.449 48…＜p＜3.544 09…时，当k→∞，系统(1)存在四个平衡点；

在3.544 09…＜p＜3.564 4… 时，当k→∞，系统(1)包含八个平衡点。

随着p值的不断增加，系统呈现稳定的2，4，8，16，…2n周期分叉点，同时周期轨道在稳定时对应的p值取值范围不断缩小，直到混沌。

针对系统(1)，控制器可以设计成不同的形式，如线性控制器、非线性控制器、状态反馈控制器，根据实际需要选用不同类型的控制。线性控制器可以设计为u=k1·x，非线性控制器可以设计为u=k1·x+k2·x2,那么加入控制器后的动力系统变为

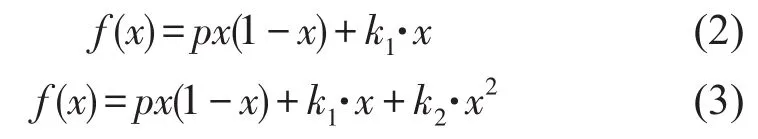
1.1 线性控制器

首先考虑系统(2)，当k1=0时，受控系统(2)退化为原系统(1)[1]。

通过对比图1—图4，说明线性控制器不仅可以控制系统(1)的倍周期分叉，对混沌特性同样起到控制作用。在k1=-0.7时，受控系统(2)没有出现混沌。在p∈[0,3.9]区间内只有一次倍周期分叉出现。在k1=-0.4时，系统(2)的混沌特性同样得到控制，且在p∈[0,3.9]区间内出现了两次倍周期分叉。当k1=+ 0.7时，系统(2)的分叉和混沌行为提前了，这没有起到抑制或延迟分叉出现的目的。根据选用不同的控制器，可以总结出当k为适当的正整数时，只能使得系统(2)的分叉和混沌行为提前。只有当线性控制器为负数时才能起到延迟分叉出现的目的。

控制参数k1=-0.7时，在p=3.693位置，受控系统(2)出现第一次倍周期分叉，较系统(1)的首次倍周期分叉向后延迟了0.693。

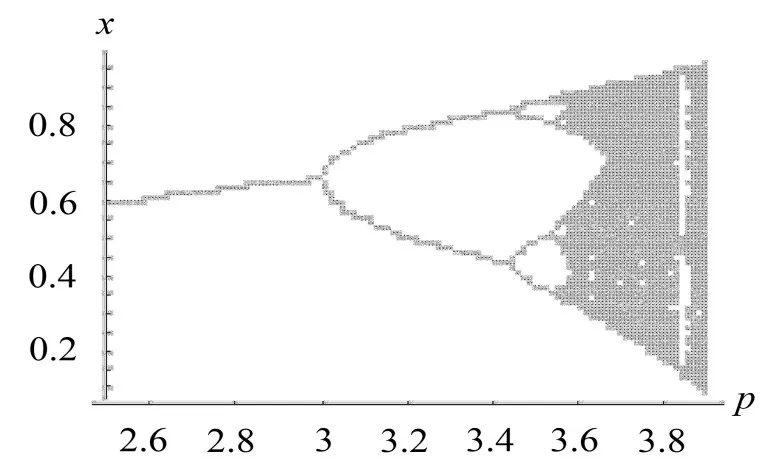
图1 系统(1)的分叉图

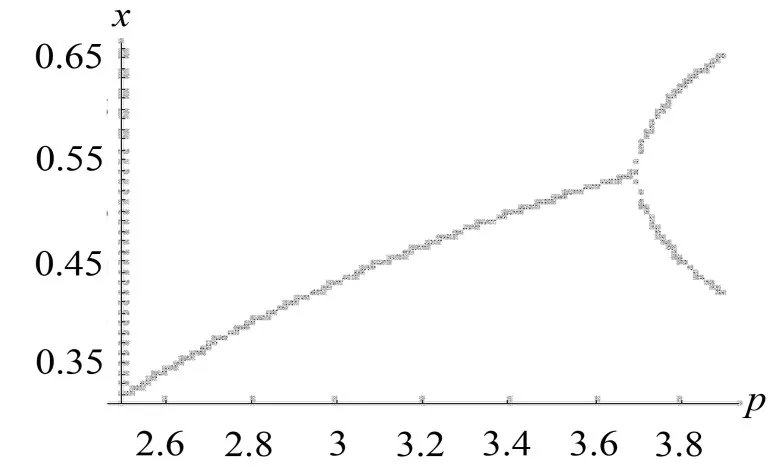
图2 k1=-0.7时系统(2)的分叉图

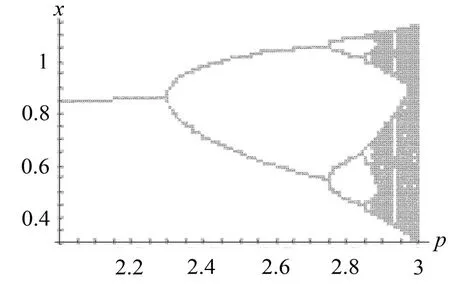
图3 k1=+0.7时系统(2)的分叉图

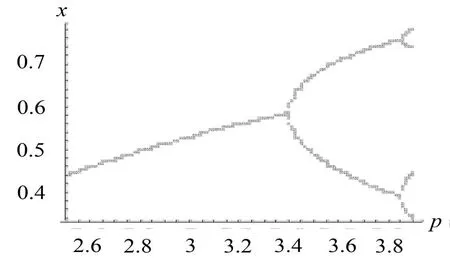
图4 k1=-0.4时系统(2)的分叉图

控制参数k1=-0.4时，在p=3.395位置，受控系统(2)出现第一次倍周期分叉，较系统(1)的首次倍周期分叉向后延迟了0.395，在p=3.849时，系统(2)第二次倍周期分叉出现，第二次倍周期分叉向后延迟了接近0.4。

当k1=+0.7时，系统(2)在p=2.29出现第一次周期倍分，p=2.747出现第二次周期倍分。两次周期倍分的出现较受控系统均有所提前。

1.2 非线性控制器

在系统(3)中。当k1=0和k2=0时，受控系统(3)退化为原系统(1)，当k2=0时，在系统(3)退化为原系统(2)。

由图4、图5可以看出所设计的非线性控制器都延迟了所有周期倍分的产生。当k1=-0.4，k2=2.2时，在区间p∈[0,3.9]，系统(3)混沌特性消失，同时出现两次周期倍分。当k1=-0.7，k2=1.1时，在区间p∈[0,3.9]，系统(3)的混沌特性得到控制，在区间内只发生了一次倍周期分叉。在控制过程计算表明，控制器中的k1可以大幅度控制系统的分叉行为，承担粗调的功能。控制参数k2在控制器中承担微调的功能，意味着k2可以精确调节分叉控制，充分发挥控制参数k1和k2的功能，可以有效控制系统的分叉。

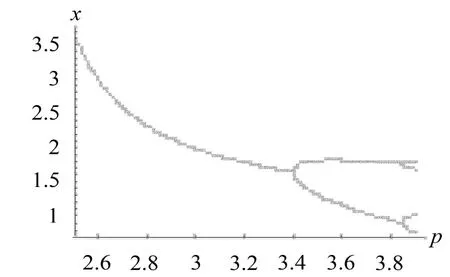
图5 k1=-0.4,k2=2.2时系统(3)的分叉图

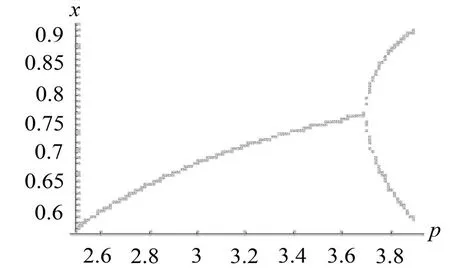
图6 k1=-0.7,k2=1.1时系统(3)的分叉图

当控制器选择为u=2.2·x2-0.4·x时，受控系统(3)在p=3.393出现第一次周期倍分，较未受控系统第一次周期倍分延迟了0.393，在p=3.847出现第二次周期倍分，较未受控系统第二次周期倍分延迟了0.398。

当控制器选择为u=1.1x2-0.7·x时，当p=3.691时受控系统(3)第一次周期分叉出现，相对于系统(1)第一次周期倍周期分叉向后延迟了0.691。

1.3 状态反馈控制

对原系统xk+1=f(xk,p)实施状态反馈控制，控制系统为

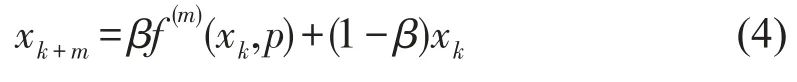
式中β为控制参数，m是正整数，0＜β＜1，当 β=1时，受控系统(4)退化为原系统(1)，在这里受控系统(4)与未受控系统具有相同的m周期轨道。这是因为系统(1)经过m次迭代后变为

当系统(1)有m周期轨道时，令xk+m=xk=x，则(5)式满足

状态反馈控制的系统(4)具有m不同周期分叉特性，从而经(4)式可以得到m周期轨道应满足如下方程

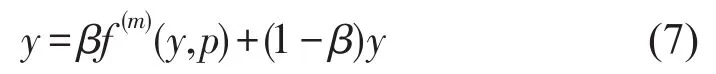
即

比较(6)和(8)，受控系统(4)与原系统(1)的m周期轨道满足相同的方程。本文只考虑m=1的情况。

由图7—图10可知，通过适当的选择调控参数β可以使分叉发生在指定的p值点上，从而使系统的分叉被延迟或被完全消除。

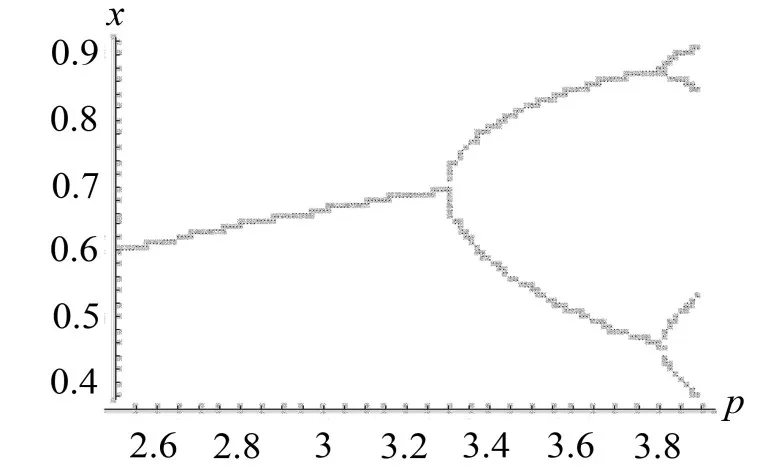
图7 β=0.87的分叉图

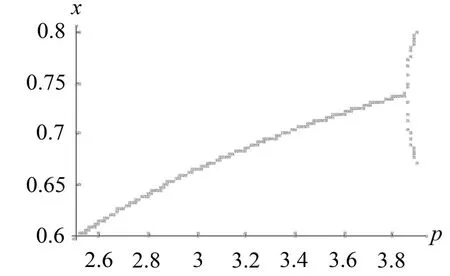
图8 β=0.7的分叉图

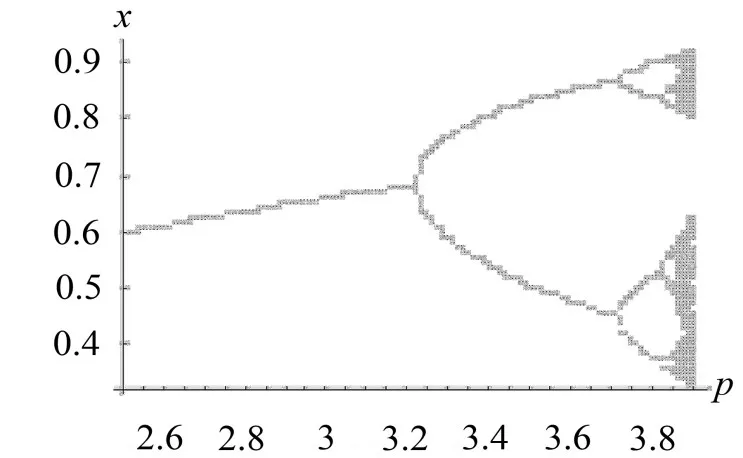
图9 β=0.9的分叉图

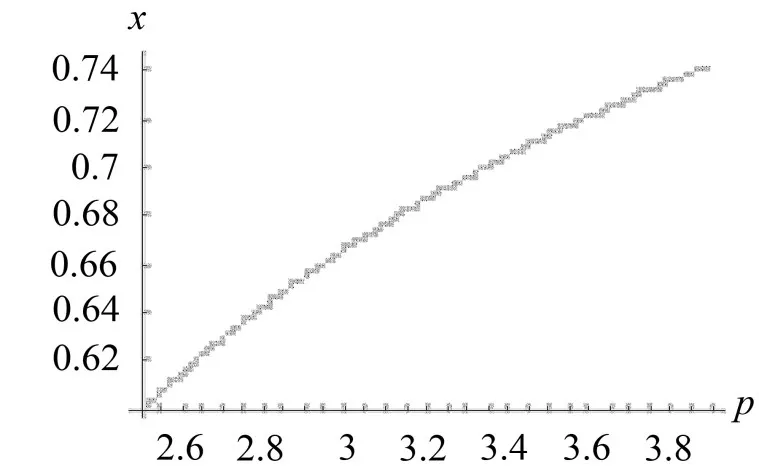
图10 β=0.5的分叉图

2 结语

设计了线性控制器，非线性控制器以及状态反馈控制器，有效的控制了非线性动力系统的倍周期分叉。设计的线性控制器和非线性控制器由粗调和微调两部分组成，可以使系统分叉得到有效控制。同时状态反馈控制也有效地的实现了对非线性动力系统的倍周期分叉控制。

[1]唐驾时,欧阳克俭.Logistic模型的倍周期分叉控制[J].物理学报，2006，55(9)：4467-4441.

[2]符文彬,唐驾时.基于状态反馈参数激励系统的超谐共振分叉控制[J].物理学报，2004，53(9)：2889-2893.

[3]CHEN G,Moiola J L,WANG H O.Bifurcation control: theories,methods,andapplications[J].International Journal of Bifurcation and Chaos,2000,10(3):511-548.

[4]Tesi A,Abed E H,Genesio R,WANG H O.Harmonic balance analysis of period-doubling bifurcations with implicationsforcontrolofnonlineardynamics[J].Automatica,1996,32(9):1225-1271.

[5]Alvarez J,L.Curiel E.Bifurcations and chaos in a linear controlsystemwithsaturatedinput[J].International Journal of Bifurcation and Chaos,1997,7(8):1811-1822.

[6]WANG H O,Abed E H.Bifurcation control of a chaotic system[J].Automatica,1995,31(9):1213-1226.

[7]Nayfeh A H,Harb A M,Chin C M.Bifurcations in a powersystemmodel[J].InternationalJournalof Bifurcation and Chaos,1996,6(3):497-512.

[8]Cam U,Kuntman H.A new CCII-based sinusoidal oscillatorprovidingfullyindependentcontrolof oscillation condition and frequency[J].Microelectronics Journal,1998,29(11):913-919.

[9]Basso M,Evangelisti A,Genesio R,Tesi A.On bifurcation control in time delay feedback systems[J].International Journal of Bifurcation and Chaos,1998,8:713-721.

[10]Brandt M E,Chen G R.Bifurcation control of two nonlinear models of cardiac activity[J].IEEE Circuits System I,1997,44:1031-1034.

[11]俞 翔，朱石坚.硬刚度特性非线性隔振系统分叉的数值研究[J].噪声与振动控制，2003 23(5)：5-9.

[12]邓瑞基，陈自力，石立群.集中荷载作用下悬索的三次超谐波共振分析[J].噪声与振动控制，2010 30(4)：13-17.

[13]符文彬，唐驾时.强迫Duffing振动系统的主共振鞍结分叉控制[J].振动工程学报，2004，17(3)：365-368.

[14]Moiola J L,Desages A C,Romagnoli J A.Degenerate Hopf bifucationsvia feedback system theory:higher orderharmonicbalance[J].ChemicalEngineering Science,1991,46(5-6):1475-1490.

[15]Alhumaizi K,Elnasharie S E H.Effect of control loop configuration on the bifurcation behavior and gasoline yield of industrial fluid catalytic cracking(FCC)units[J].Mathematical and Computer Modelling,1997,25(3):37-56.

[16]Ouyang K J,Tang J S,Liang C X.Amplitude control of limit cycle in a van der Pol-Duffing system[J].Chinese Physics B,2009,18(11):4748-4753.

[17]Ji J C and Leung AY T.Resonances of a non-linear s.d.o.f.system with two time-delays in linear feedback contro1 [J].Journal of Sound and Vibration,2002,253(5):985-1000.

[18]欧阳克俭.非线性动力系统的两类分叉控制与混沌控制研究[D].长沙：湖南大学硕士论文，2007.

Period-doubling Bifurcation Control of Discrete Nonlinear Dynamic System

OUYANG Ke-jian1,TANG Jia-shi2

(1.Institute of State Grid Hunan Electric Power Corporation,Changsha 410007,China; 2.Department of Engineering Mechanics,Hunan University,Changsha 410002,China)

This paper studies the control of period-doubling bifurcation of discrete nonlinear system,designs of linear controller and nonlinear controller,and state feedback control method to control nonlinear dynamical systems.The bifurcation diagrams before and after the control are obtained,so that the desired bifurcation control purposes of the system can be achieved.According to the purpose of actual application,different controllers can be designed.The linear controller and non-linear controller consist of two portions of rough tuning and fine tuning,so that bifurcation of the system can be controlled effectively.Selecting appropriate controller and effective control parameters,the state feedback can yield good results for the bifurcation control.

vibration and wave;period-doubling bifurcation;bifurcation control;state feedback control;bifurcation diagram

1006-1355(2014)03-0057-04

A

10.3969/j.issn.1006-1335.2014.03.012

随着非线性科学的发展，物体的分叉和混沌的行为不断得到深入理解和认识，结构的非线性动力学分叉控制的研究成果在许多工程领域中得到了应用。如气象[1，2]、机械工程[3―14]、以及化学工程[15，16]等方面。近十多年来，分叉控制越来越得到学者们的重视，分叉控制逐渐形成了一个新的控制论方向，同时显示其可观的前景和巨大的潜力。分叉控制主要指对目标系统施加控制器，改变结构的非线性动力性能，达到预期的控制目的。分叉控制的主要方式有[17，18]：将分叉链的形状和类型进行修改；使系统的分叉解趋于稳定；产生新的分叉或使分叉的出现延迟；使系统极限环幅值或频率得到控制；控制系统的动力学不稳定解所在区域缩小；通过系统的分叉混沌特性实现分叉控制达到控制混沌的目的，等。本文主要是针对于一类非线性离散动力系统设计不同类型的控制进行分叉控制，也可达到控制混沌的目的。

2013-08-09

国家自然科学基金资助：无限维非线性系统的分岔控制（11172093）

欧阳克俭（1981-），男，工学博士，湖南娄底人；主要从事非线性振动与输变电结构技术研究。

E-mail:kjouyang@gmail.com