用混沌参数甄别车辆悬架振动信号的周期性

彭富明，汪正杰，张 雨，王玉国，吴 凯

（1.南京理工大学 自动化学院，南京210094；2.南京工程学院 机械工程学院，南京211167）

用混沌参数甄别车辆悬架振动信号的周期性

彭富明1，汪正杰1，张 雨2，王玉国2，吴 凯1

（1.南京理工大学 自动化学院，南京210094；2.南京工程学院 机械工程学院，南京211167）

悬架—车轮系统隔振参数选择的正确与否取决于系统振动信号周期性的好坏，而单纯用肉眼无法有效判别振动信号周期性的差别。用Grassberger-Procaccia（G-P）算法和小数据量法合理选择嵌入维数、延迟时间和序列平均周期等重要参数，并且在对数曲线图中准确划定无标度区，以得到比较客观的关联维数和最大Lyapunov指数。结果表明：采用关联维和最大Lyapunov指数作为判据，可以对悬架—车轮系统振动信号作周期性甄别，从而更准确地评价汽车悬架隔振性能。

振动与波；悬架—车轮系统；周期性甄别；关联维；Lyapunov指数；汽车隔振参数

运用混沌特征参数描述车辆悬架系统的振动响应信号，是基于非稳态非线性动力学系统的混沌性质。关联维数D2能够定量地描述事物内部结构的复杂程度，最大Lyapunov指数λmax是刻画奇异吸引子性质的一种测度和统计量，是针对系统的运动轨道而言的。它们反映了混沌系统中奇异吸引子的整体变化情况，适合于描述属于非稳态非线性动力学系统的车辆悬架系统的混沌性质。本文对悬架—车轮系统的振动信号进行相空间重构，计算其关联维数和最大Lyapunov指数来甄别振动信号周期性好坏，从而引入了一类新的车辆悬架系统振动信号周期性判据。

1 甄别悬架—车轮系统振动响应信号周期性的原理

对悬架-车轮系统振动响应信号进行计算处理，能够得到悬架隔振参数族，包括阻尼比、悬架效率、左-右轮悬架效率差、固有频率。

计算悬架隔振参数的正确性有赖于对悬架-车轮系统振动响应信号计算某超调量下阻尼比ξ的准确性，其前提是悬架—车轮系统属于2阶线性欠阻尼系统[3]，即悬架阻尼比ξ＜1。当对该系统施以拟脉冲激励后，其振动响应信号的理想形态以有阻尼固定频率做产生等周期衰减振动，如图1所示。但是对于实际的悬架—车轮系统，汽车悬架的刚度和阻尼往往设计成非线性，以适应不同的路况和载重量，所以上述前提并不存在。因此，施以拟脉冲激励后，振动响应信号实际上具有变周期衰减振动的形态，振动过程中振幅越来越小，周期也越来越小。

为了计算某超调量下的阻尼比ξ，可采用关联维D2和最大Lyapunov指数λmax作为判据，对悬架—车轮系统振动响应信号作周期性甄别。根据混沌理论[4,5]，对周期性强的信号，D2近于1，而λmax较小；反之，对于周期性弱的信号，D2远离1，而λmax较大。

2 基于关联维与最大Lyapunov指数进行周期性判别

2.1 G-P算法

G-P算法[6,7]是Gtassberger和Procaccia提出的一种比较普遍的求取系统关联维的方法，其中的关联维指的是吸引子真正维数的估计值。相空间重构之后，定义关联积分函数为

式（1）中：ri，j=d(Xi-Xj)=‖Xi-Xj‖，即任选一个基准向量Xi，计算Xi到其余各点之间的距离，对所有Xi(i=1，2，...，N）重复这一过程，得到所有点对的间距；r为无标度观测尺度；θ(u)为Heaviside函数，即

图1 悬架—车轮系统振动理想响应信号

关联积分函数表示当变量r一定时，重构相空间X中的所有点对之间距离小于r的点个数占所有点的多少。适当地选取r，在无标度区内存在D为关联维数。

计算关联积分后绘制l nCm(r)-l n(r)曲线，对其用直线拟合后的直线斜率即为相空间中奇异吸引子的关联维。

混沌系统的关联维D2为一个正的分数。不同的D2值对应不同的系统状态：D2=1系统呈现出周期振荡状态，在相空间中是一条封闭曲线；D2=2系统是有两个不可约频率的周期振荡；D2是分数时，系统处于混沌运动状态。

2.2 小数据量方法计算最大Lyapunov指数

在重构的相空间中，寻找每个参考点Xj的最近邻点即

为了避免参考点Xj和最近邻点位于同一轨线上，这里采用限制短暂分离，即要求

其中p为时间序列的平均周期，它可以通过功率谱的平均频率的倒数估计出来。对相空间中的每个点，计算出该临近点对的第i个离散时间步长后的

距离

假定第j个最近邻点近似以λ1的速率指数发散，即

对其两边取对数，得

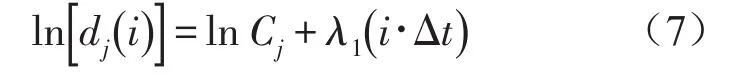
由(7)式可以看出，ln[dj(i)]—i曲线在一定范围内满足线性关系，其曲线的斜率为λ1Δt。

因此固定i，对所有j对应的ln[dj(i)]求平均再除以Δt，得到y(i)

2.3 验证程序的正确性

根据上述关联维和最大Lyapunov指数的算法，在MATLAB软件中编写了计算混沌参数的程序，对于编写的算法程序，又采用正弦信号作为考核案例，来验证它的准确性。图2为不同嵌入维数双对数曲线，从图中可以看出，最小嵌入相空间维数m从2开始，无标度区曲线开始趋于一致，关联维数处于稳定状态，故选择m=2。图3为最小嵌入维数为m=2时的y(i)—i曲线，无标度区直线斜率即为最大Lyapunov指数。由程序计算得关联维数D2=1.056 416，最大Lyapunov指数λmax=0.010 3。可以看出，D2接近于1，λmax接近于0，考核结果基本符合确定的周期系统的特性，从而验证了程序的正确性。

图2 不同嵌入维数双对数曲线图

图3 m=2时的y(i)—i曲线图

3 悬架—车轮系统振动信号的周期性判别

3.1 悬架—车轮系统振动时域信号

每次人工按压后获得的时域波形相似，单纯用肉眼无法判别出信号周期性差异。如图4所示为悬架—车轮系统振动信号时域图，图（a）为信号周期性好的时域图，图（b）为信号周期性差的时域图，两图形非常相似，差别不明显，无法用肉眼判别周期性好坏。由此，可用已验证正确的MATLAB程序计算出关联维和最大Lyapunov指数，来判别信号周期性好坏。

3.2 参数选择

（1）一维数据序列长度n的确定

图4 悬架—车轮系统振动信号时域图

Eckmann等人1992年曾指出计算关联维数与所用数据的长度有关，近似为其中d为重构吸引子的直径，D为关联维数D2的估计值，r为标量。由以上所得的数据序列长度的值一般较大，在关联维计算中，实际的数据序列长度往往受许多客观条件的限制如数据来源的限制。所以，数据序列长度的选取须根据数据来源等具体情况和分形数值分析的需要来定。

考虑被测悬架系统的固有频率上限小于25 Hz，设定采样频率为50 Hz，采样点数为512点，所以采样时间为1/50×512=10.24(s)，而施加拟脉冲激励后汽车悬架振动过程仅需两三秒钟，所以数据采集卡能完全采集到悬架振动的信号全过程。而采集512个点，对于本实验已经足够。

（2）时间延迟的确定

延迟时间的选取原则是让时间序列内元素之间的相关性减弱，同时又要保证时间序列包含的原系统的信息不会丢失。研究表明，当关联函数的值第一次为0（或近似为0）对应的延迟时间比较合适，设定为最佳时延。经过验证，不同悬架—车轮振动信号样本的延迟时间相差不大。在τ=11情况下，悬架—车轮振动信号的自相关函数图如图5所示。

图5 自相关函数曲线

（3）嵌入维数m的确定

嵌入维数m是指能完全包容吸引子的最小子空间维数，它是重构相空间的一个重要参数。当关联维达到饱和以前随着相空间维数m的增加，所得到的关联维数也在增加。取饱和时对应的m为嵌入维。对于本实验测得的悬架—车轮振动信号数据，经计算得出关联维饱和时对应的嵌入维数为6。

3.3 无标度区的确定

3.3.1 关联维无标度区判定

将双对数曲线中直线度较好的区间定义为无标度区。一般无标度区的确定采用肉眼判别法，简单快速。例如图8中无标度区可选取[0.4，0.7]。

对于悬架—车轮振动响应同一组信号，不同嵌入维数双对数曲线变化图及无标度区，如图6所示。图中曲线从上到下对应嵌入维m分别为2、4、6、…，20，依次相差2。从图8可知：无标度区曲线随着m的增加趋于平行或者重合，也验证了随着m的增大，关联维数趋于稳定状态；当m为6时，双对数曲线趋于一致，故在悬架—车轮振动数据处理时，选择m=6。

图6 不同嵌入维数双对数曲线变化图及无标度区

3.3.2 最大Lyapunov指数无标度区判定

前面指出，选择曲线y(i)—i的一段线性区域，并用最小二乘法作出回归直线，该直线的斜率就是最大Lyapunov指数λmax。考虑f=y(i)的1阶导数

理想情况下，如果y(i)—i满足线性关系，那么f′应该为一常值。因此，在曲线y(i)—i最终达到饱和之前，选取曲线y(i)-y(i-1)—i随i的变化相对较小的区域即是理想的线性区域。图7中，图（a）为y(i)—i曲线图，图（b）为y(i)的1阶导数曲线图。

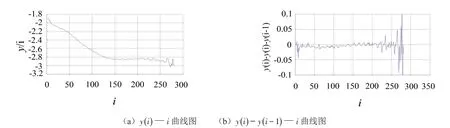
图7 最大Lyapunov指数

在图7（b）中，当i=50—150时，曲线y(i)-y(i-1)—i几乎为一常值，说明曲线y(i)—i的斜率相对稳定。因此，悬架—车轮振动信号的线性区域取[50，150]。

3.4 实例分析

通过加速度传感器获得按压车体时悬架-车轮系统振动的加速度，得到8个信号样本。用已验证正确的matlab程序分别对8个样本进行计算处理，得到8组D2和λmax值。表1所示是8个样本按计算出的D2值由大到小排序的结果。

根据混沌理论，对周期性强的信号，D2近于1，而λmax较小；反之，对于周期性弱的信号，D2远离1，而λmax较大。

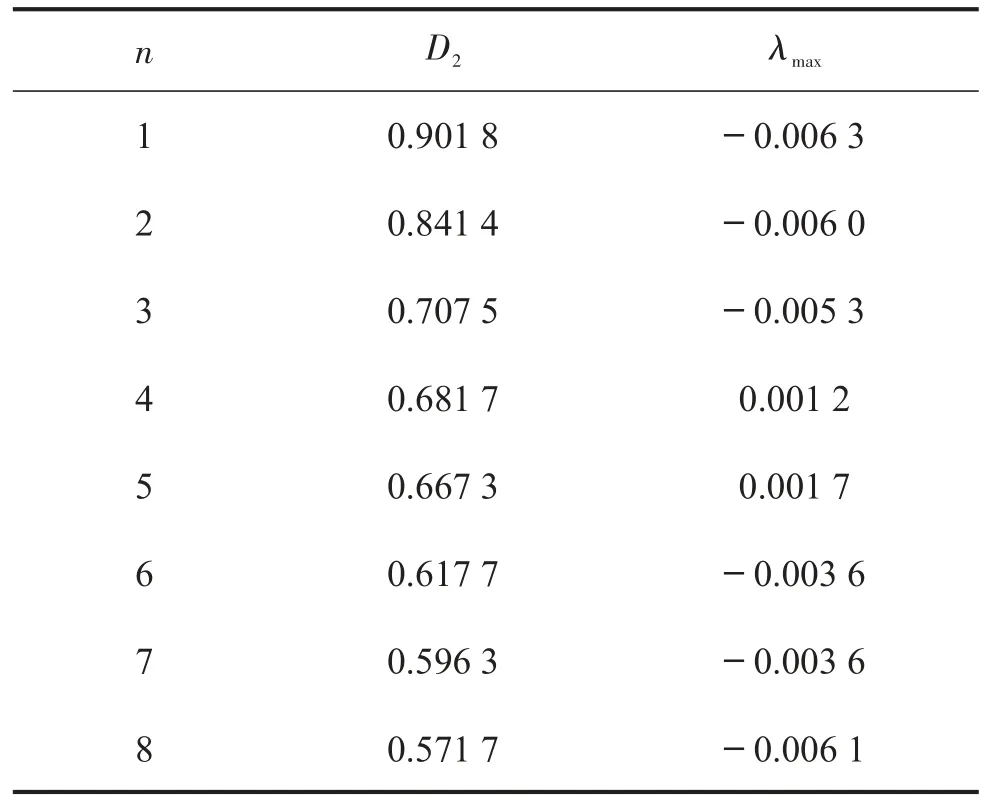
表1 一汽大众响应信号样本的D2和λmax

由表1可见：样本1—8的λmax都接近于0，差别太小，且考虑计算结果误差的原因，不具可比性，不能独立反映周期性强弱，可用来辅助D2进行判断；而D2依次减小，差别明显，说明周期性越来越差。我们设定D2＞0.7的样本是合格的样本，可依此挑选出周期性比较好的样本，即样本1、2、3，而剔除掉其余周期性较差的样本。

4 结语

1）单纯用肉眼无法判别悬架-车轮振动信号时域图的周期性差异，可采用关联维D2和最大Lyapunov指数λmax作为判据，对悬架—车轮系统振动响应信号作周期性甄别；

2）合理选择嵌入维数、数据长度、延迟时间、序列平均周期等重要参数，并且在曲线图中准确划定无标度区才能得到比较客观的关联维数和最大Lyapunov指数，从而正确评价信号的周期性；

3）在曲线最终达到饱和之前，曲线[y(i)-y(i-1)]—i随i的变化相对较小的区域即是理想的线性区域；

4）未知matlab程序是否正确的情况下，先用正弦信号进行验证。对正弦信号的计算结果表明，编写的matlab程序是正确可行的；

5）本文所用周期性判别方法不只用于悬架-车轮系统，对其它信号也适用，具有广泛用途。

[1]Frision,T.,Abarbanel,H.D.I,Cembrola,J.Ang Katz,R.Nonlinear analysis of environment distortions of continuous wave signals in the ocean[J].Journal of the Acoustical Society of America，1996,99(1):139-146.

[2]Turcotte,D.L.Fractals in geology and geophysics[J].Pure and Applied Geophysics,1989,131(1/2):171-196.

[3]李杰敏.汽车拖拉机实验学(2版)[M].北京：机械工业出版社，1998:26-27.

[3]Li Jiemin.Automotive tractor experimental subject[M].Version 2.Beijing:Mechanical Industry Press,1998:26-27.

[4]LIU W Y,ZHU W Q,HUANG Z L.Effect of bounded noise on chaotic motion of doffing oscillator under parametric excitation[J].Chaos,Solitons and Fractals, 2001,12（3）:527-537.

[5]Barrett M D.Continuous control of chaos[J].Physica D: Nonlinear Phenomena,1996,91（4）:340-348.

[6]Peter G，Itamar P.Characterization of strange attractors [J].Physical Review Letters,1983,50(5):346-349.

[7]王庆华，张兴彪，张洪朋，等.分形理论在液压泵故障诊断中的应用[J].大连海事大学学报，2004，30(2)：40-43.

[7]WANG Qin-hua,ZHANG Xin-biao,ZHANG Hong-peng, and so on.Application of fractal theory to fault diagnosis for hydraulic pump[J].J ournal Dalian Maritime University,2004,30(2):40-43.

[8]M.T.Rosenstein,J.J.Collins and C.J.De luca.A practical method for calculating largest Lyapunov exponents from small data sets[J].Physica D,1993,65: 117-134.

Distinguishing the Vibration Signal’s Periodicity of Vehicle’s Suspension System Based on Chaotic Parameters

PENG Fu-m ing1,WANG Zheng-jie1,ZHANG Yu2, WANG Yu-guo2,WU Kai1

(1.School ofAutomation,Nanjing University of Science and Technology,Nanjing 210094,China; 2.School of Mechanical Engineering,Nanjing Institute of Technology,Nanjing 211167,China)

The correctness for calculating the anti-vibration parameters of a suspension-wheel system depends on the quality of periodicity of the vibration signals of the system.But simply using the naked eyes can not effectively distinguish the periodicity differences of the vibration signals.In this article,the Grassberger-Procaccia(G-P)algorithm w ith small data sets is adopted to reasonably choose the embedding dimension,reconstruction delay,mean period of the time series and some other important parameters.And the scale-free zone is accurately delim ited in the logarithm ic-curve diagrams to get fairly objective correlation dimension and the maximum Lyapunov exponent.The results show that the correlation dimension and the maximum Lyapunov exponent can be used as criteria to distinguish the periodicity of the vibration signals for the suspension-wheel system,so that the vibration isolation performance of automobile’s suspensions can be evaluated more accurately.

vibration and wave;suspension-wheel system;periodicity distinction;correlation dimension;Lyapunov exponent;anti-vibration parameters of auto

1006-1355(2014)04-0104-05

TB53；U463.33；O415.5 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.023

自混沌现象发现以来，混沌已被证实是广泛地存在于自然系统和人工系统当中的一种非线性现象。汽车悬架是典型的非线性系统，由于结构的复沌。混沌特征参数关联维因其良好的特征性，通过重构相空间与非线性问题建立了联系，近年在水声信号处理[1]、地震信号处理[2]、机械故障诊断等领域得到应用。最大Lyapunov指数在腐蚀深度预测、城市用水量预测、边坡位移预测等领域获得了很好的效果。因此，关联维和最大Lyapunov指数作为解决复杂非线性问题的重要方法具有广阔的应用前景。

2013-10-10

2012年度江苏省高校科研成果产业化推进工程项目（项目编号：JHZD2012-6）江苏省自然科学基金BK20130746

彭富明（1965-），男，江苏宜兴人，高级工程师，硕士生导师。现从事车辆测量与控制、汽车电子研究。

汪正杰，男，硕士研究生。

E-mail:842956715@qq.com