主动结构的控制律辨识研究
刘海标,宋汉文
(同济大学 航空航天与力学学院,上海200092)
主动结构的控制律辨识研究
刘海标,宋汉文
(同济大学 航空航天与力学学院,上海200092)
主动控制结构主要运用于包括振动、声学、转子动力学的一些工程项目中。对于各种主动结构,其控制律显然是最能反映主动结构动力学特征的参数。在对相关参数进行了初步的探讨后,得到了在单点控制单点反馈条件下,对其反馈信号类型及其反馈增益的辨识公式。该方法由频响函数直接构造,其表达简洁,具有一定的工程实用价值。通过实例的数值计算也证实了该方法的正确性。
振动与波;主动结构;控制律辨识;频响函数
为了深刻地认识主动结构,就一定要研究主动结构的控制律。本文明晰了控制律所涉及的范畴,并针对某一特定的范畴的控制律的辨识,进行了理论推导,得到了一个简单有效的辨识公式。并通过仿真和实验对所得的公式进行了验证,证明其正确性。
1 控制律
对于单自由度主动结构,控制律只涉及反馈信号的类型以及反馈增益的大小。然而,对于多自由度离散系统的主动结构中,构成“控制律”模型的要素包括:为作动器提供反馈信号的参考点的位置与数量、作动器施加激励点的位置与数量、描述每个作动器输入输出关系的微分方程或传递函数模型及其参数。
本文的控制律辨识的情形是:对于单点控制单点反馈的主动结构,在作动器和反馈信号参考点的位置已知的情况下,对其控制反馈信号的种类及其增益大小进行辨识。
2 辨识原理
2.1 控制律与频响函数的关系
在所有的主动结构中,线性主动结构是一种最简单的理想系统。考察多自由度系统:

[M]、[C]、[K]分别为质量、阻尼及刚度矩阵,{f(t)}与分别定义为开环和闭环载荷。其中:

[P]、[D]、[S]分别为闭环荷载加速度项、速度项及位移项的系数矩阵,闭环荷载亦可表述为如下形式

由公式(2b)可知:施加在任意自由度上的闭环控制力,均可表达为所有测点上的位移,速度以及加速度响应的线性组合。将独立的作动器连接到被控制测点,按照设计要求把测得的位移、速度和加速度响应进行的相应的线性组合,进而获得激振力,即可实现这种系统。把(2a)代入(1)式,可得

从上述结论可知,一般来说,主动结构的系数矩阵不再对称,且同时需要判定系统的稳定性。主动结构的系数矩阵的非对称性会导致主动结构频响函数矩阵对称性的破坏,还会使得主动结构的左右特征向量的差异。在主动结构的实验模态分析与参数辨识领域,本文将限于结构的稳定区域内进行研究。
不失一般性,时域方程(1)在r点测量p点控制的情况下,主动结构的频域方程为

设反馈增益函数为

其中Δkpr,Δmpr和Δcpr分别为刚度矩阵、质量矩阵及阻尼矩阵的第p行,第r列的改变值,也就是所要求的反馈增益系数。
令位置分配矢量

其中{up}的第p个元素为1,其余元素为0,{vr}的第r个元素为1,其余元素为0。那么{up}{vr}T为n×n阶矩阵,其中第p行,第r列的元素为1,其余元素为0。
式(4)可进一步变成如下形式

则主动结构的频响函数可表达为如下形式

由Sherman–Morrison公式[15]

则可以推出主动结构的频响矩阵与原被动结构的频响矩阵之间存在如下关系

为了进一步得到主动结构的频响函数与原被动结构的频响函数的关系,在式(9)左右两端同时左乘{vm}T,右 乘{un},由 于{vm}T[H(ω)]{un}=Hmn,整理可得

将上式中的m、n互换,可知主动结构频响函数矩阵的对称性已经被破坏。
2.2 基本辨识表达式
令m=r,式(10)可以化为如下形式

从式(24)可以推导出控制增益的表达式为

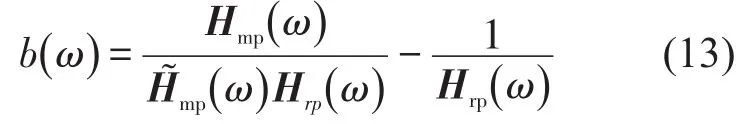
特殊地,令m=r,n=p,则式(10)可以化为如下形式

同理,令n=p,式(10)可以化为如下形式

从以上推导式可见:
(1)观察式(5)与式(15)中函数的下标可以看出,所用频响函数的下标与待求的原系数矩阵被改变元素的位置的下标具有对称性;
(2)由式(5)及式(15)可知,为了求得b(ω)中的增益系数Δkpr,Δcpr及Δmpr,只需和Hrp(ω)取两个同频率点的值,即可求得Δkpr,Δcpr及Δmpr。在实际实验中,由于实验存在误差,所以,取尽可能多的点应用最小二乘法来求得增益系数。
从式(14)可以推导出控制增益的表达式为
公式(12)、(13)和(15)都可用于辨识系统的反馈增益,公式(15)是所有表达中最为简洁的。然而,在获取结构的频响函数的时候,由于机械系统的几何构型,整体的工艺要求,现场的测试条件等诸多原因,很多时候,有一些点的频响函数是很难获得的。此时,就要结合现场的实际情况,选取合适的公式进行辨识。对于下面的数值算例来说,不存在上述问题,处于验证算法的正确性的目的,下面将选取相对比较简单的式(15)进行主动结构的控制律的辨识。
3 数值算例
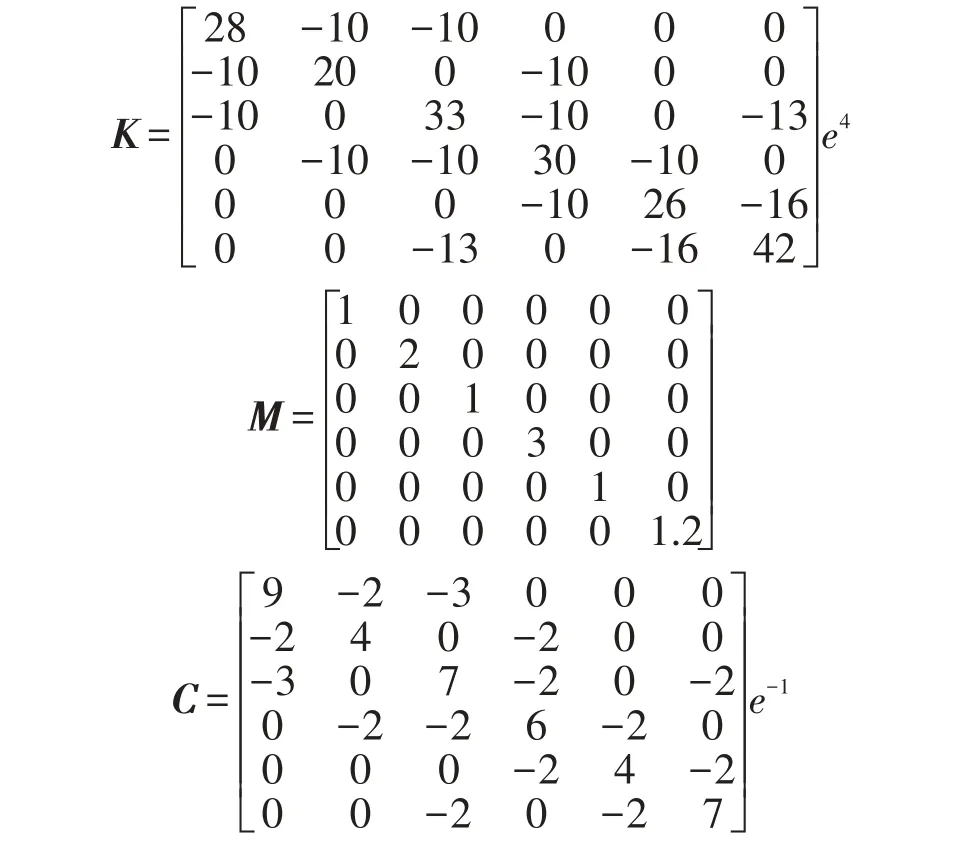
构建如图1所示的弹簧—质量—阻尼系统,然后从m 5取信号,施加于m 2,反馈的加速度,速度和位移的信号分别为-1,-2 000,-0.5,形成主动结构。原被动结构及相应的主动结构的刚度矩阵,质量矩阵及阻尼矩阵分别为:

图1 六自由度弹簧—质量—阻尼系统
由第2节可知,为了得到原系数矩阵第2行,第5列的变化量,即控制律,需要获得原被动结构的频响H52及相应的主动结构的频响
仿真中,H52及的对数频响幅值图如图2所示。
将b(ω)=-(Δkpr+jωΔcpr-ω2Δmpr)带入式(15)中,每一对被动频响H52及主动频响H˜52的对应点都可以组成一个待解方程,但在实际应用时,为了保证了数值计算的稳定,取尽可能多的频响函数点,运用最小二乘原理将矛盾方程转化为定解方程,就可计算Δkpr,Δcpr及Δmpr。
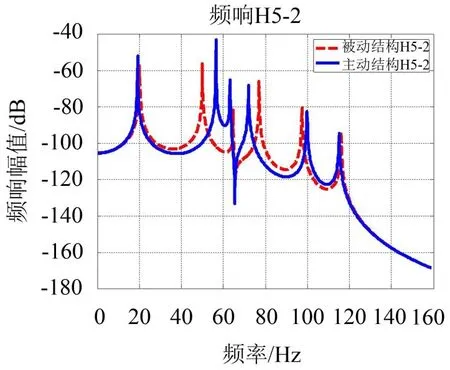
图2 被动结构和主动结构的频响
应用上述方法辨识得到阻尼、质量及刚度阵对应位置的改变量分别为 Δc25=-4.999×10-1,Δm25=-1.000×100,Δk25=-2.000×103,与所施加的控制律相吻合。
4 结语
(1)本文对单自由度以及多自由主动结构的控制律进行了简扼的阐述,提出了辨识主动结构的控制律的问题的关键点和难点所在;
(2)对于单点控制单点反馈的主动结构,在已知控制点和反馈点的位置关系的条件下,可利用主被动结构的频响函数对主动结构的控制律进行辨识,辨识的控制律内容包括:反馈信号的类型,即加速度、速度和位移反馈,各种类型的反馈信号的增益等;
(3)该方法有以下三方面的优势1)不需重构主动结构与原被动结构的质量、刚度和阻尼矩阵;2)避免对频响函数矩阵直接求逆;3)直接利用实验测得的主被动频响函数的对应点进行拟合,省掉对频响函数曲线进行拟合的步骤,进而消除了曲线拟合过程中所带来的误差。
本文为更复杂的控制律辨识问题,如控制点与反馈点未知的情况以及多点控制多点反馈的情形,提供了可予借鉴的观点。
[1]Serrand M,Elliott S J.Multichannel feedback control for the isolation of base-excited vibration[J].Journal of Sound and Vibration,2000,234(4):681-704.
[2]Zarfam R,Khaloo A R.Vibration control of beams on elastic foundation under a moving vehicle and random lateral excitations[J].Journal of Sound and Vibration, 2012,331(6):1217-1232.
[3]陈继峰,程远胜.具有非线性刚度动力吸振器的隔振系统半主动控制[J].噪声与振动控制,2006,6:1-4.
[4]赵 林,葛耀君,朱乐东.台风气候大跨度桥梁风振响应研究[J].振动工程学报,2009,22(3):237-245.
[5]顾 明,陆海峰.膜结构风荷载和风致响应研究进展[J].振动与冲击,2006,25(3):25-28.
[6]师汉民.金属切削理论及其应用新探[M].武汉:华中科技大学出版社,2003.
[7]Preumont A.Vibration control of active structures[M].Dordrecht,the Netherland:Kluwer Academic Publishers, 1997.
[8]Wyckaert K,Augusztinovicz F,Sas P.Vibro-acoustical modal analysis:Reciprocity,model symmetry,and model validity[J].Journal of the Acoustical Society of America,1996,100(5):3172-3181.
[9]Adhikari S,Modal analysis of linear asymmetric nonconservative systems[J].Journal of Engineering Mechanics,1999,125(12):1372-1379.
[10]M irzaeifar R,Bahai H,Shahab S,A new method for finding the first-and second-order eigenderivatives of asymmetric non-conservative systems w ith application to an FGM plate actively controlled by piezoelectric sensor/ actuators[J].International Journal for Numerical Methods in Engineering,2008,75(12):1492-1510.
[11]Ouyang H.Prediction and assignment of latent roots of damped asymmetric systems by structural modifications [J].Mechanical Systems and Signal Processing,2009,23 (6):1920-1930.
[12]Ouisse Morvan,Foltete Emmanuel,On the properness condition for modal analysis of non-symmetric secondorder systems[J] Mechanical System and Signal Processing,2009,25(2):601-620.
[13]张景绘,龚 靖,王永刚.线性主动结构及模态(I、II) [J].应用数学和力学,2004,25(8):771-786.
[14]盛 严,龚 靖,杨正光.主动杆系结构的模态性质分析[J].噪声与振动控制,2010,10:6-9.
[15]Golub G H,Van Loan C F,Matrix computations[M].Johns Hopkins University Press,Baltimore,MD,1983.
Control Law Identification ofActive Structures
LIU Hai-biao,SONG Han-wen
(School ofAerospace Engineering and Applied Mechanics,Tongji University,Shanghai 200092,China)
Active structures are applied mainly in the engineering objects which include vibroacoustics,rotor dynam ics, or active control.The control law is the key parameter which can reflect the dynam ic characteristics of the active structures.In this paper,the control law of the active structures is discussed.A formula for identifying the type of feedback signal and its gain value is obtained under single control and single feedback conditions.The method is constructed by using the frequency response function(FRF)directly.In addition,the expression of the identification method is simple and convenient for engineering application.The result of numerical simulation of an example supports the validity of this method.
vibration and wave;active structure;identification of the control law;frequency response function
1006-1355(2014)04-0119-04
TB53;O327;TB123 < class="emphasis_bold">文献标识码:A DOI编码:
10.3969/j.issn.1006-1335.2014.04.026
承受闭环控制载荷的结构称为“主动结构”;仅承受开环载荷的结构称为“被动结构”。构成闭环控制荷载的控制律可以是认为施加的,例如各种目的的主动控制[1—3],也可以是由环境因素造成的,例如桥梁风振[4,5]和机床切削颤振[6]等。对每类主动结构都有特定的问题研究,例如飞机的颤振问题主要分析失稳速度,桥梁设计要避免产生自激振动。Preumont在《Vibration Control of Active Structures》[7]中论述的主动结构,主要以智能材料在振动控制中的应用为主。Wyckaert[8]讨论分析了振动声学中的非对称模型方程与模态分析所满足的互易律之间的关联,并对其模型的有效性进行了验证。Adhikari[9]将经典的模态分析进行扩展,使之适用于非对称非保守系统。将非保守系统的左右特征向量用与之对应的保守系统的左右特征向量的线性组合表示。将伽辽金最小误差方法和纽曼展开法结合起来,计算上述线性组合的复常量系数。M irzaeifar等[10]为计算含有不同特征值的主动结构的特征值和特征向量导数提出了一种新方法。Ouyang[11]对刚度矩阵非对称的主动结构的特征根问题进行了研究Ouisse[12]提出一种使复模态适应于非自伴随系统的方法,并进一步将该方法应用于对振动方程系数矩阵的辨识。张景绘[13]进行了一系列主动结构的理论及实验研究。盛严[14]对于主动杆系结构的模态分析问题进行了初步的探讨。
2013-09-27
国家自然科学基金重点项目(基金编号:11322009);国家自然科学基金项目(基金编号:11272235)
刘海标(1989-),男,吉林松原人,硕士,研究方向:模态分析、动力学参数辨识。
宋汉文(1961-),男,博士,教授,博士生导师。
E-mail:hwsong@tongji.edu.cn

