径向压力作用下夹层圆板自由振动理论解

廖明建，李映辉

（1.中国工程物理研究院 总体工程研究所，四川 绵阳621999；2.西南交通大学 力学与工程学院，成都610031）

径向压力作用下夹层圆板自由振动理论解

廖明建1，李映辉2

（1.中国工程物理研究院 总体工程研究所，四川 绵阳621999；2.西南交通大学 力学与工程学院，成都610031）

基于小挠度薄板理论，建立径向均布压力作用下夹层圆板的振动控制方程。采用分离变量法导出夹层圆板的固有频率及振型解析式，计算径向均布压力作用下周边固支夹层圆板固有频率和振型，讨论径向均布压力和夹心层比率对固有频率的影响。研究表明夹层圆板的固有频率随径向压力增大而减小，临界压力随阶次的增大而增大；作用径向压力的夹层圆板固有频率随夹心层比率增大，先缓慢增大，到峰值后减小，该趋势与无径向压力时相同。

振动与波；夹层圆板；固有频率；径向均布压力

本文拟基于小挠度薄板理论，建立径向均布压力作用下夹层圆板的振动控制方程，采用分离变量法导出夹层圆板的固有频率及振型的理论解。在此基础上，计算周边固支夹层圆板固有频率和振型，讨论径向压力和夹心层厚度对固有频率的影响。

1 夹层圆板力学模型

图1为径向作用均布压力P的夹层圆板模型。夹层圆板由上下两层对称约束层和夹心层组成。约束层弹性模量Ec，泊松比mc，密度rc，厚度h/2；夹心层弹性模量Ej，泊松比mj，密度rj，厚度H，夹层板等效密度ρ=(rch+rjH)/(H+h)。

图1 夹层圆板模型

假定夹层圆板各层均为各向同性材料，处于小挠度状态，径向压力与横向挠曲无关。采用如图1所示的坐标系，夹层圆板平衡方程[8]为

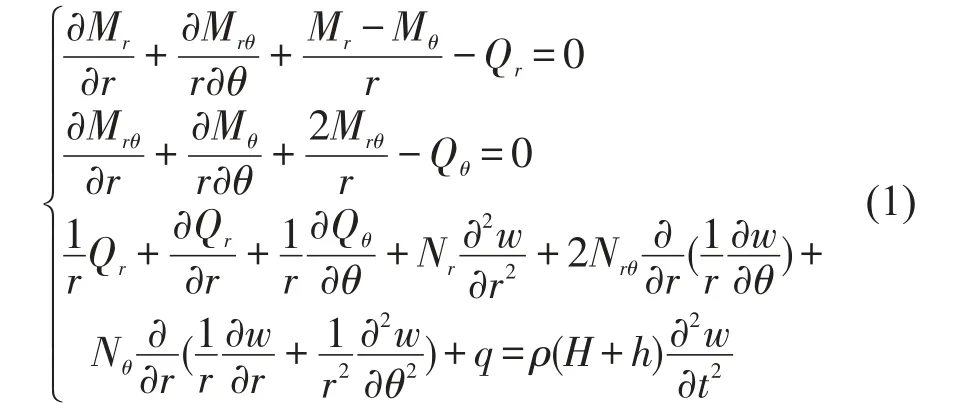
其中Nr、Nq、Nrq为相应方向的膜内力；Qr、Qq、Mr、Mq、Mrq为相应方向的剪力和力矩，w为板中面横向位移，q为横向荷载。

板内任意一点的径向、环向位移分别为

夹层板应变与挠度w关系为

各层的应力与应变关系为

其中c表示约束层，j表示夹心层。

夹层板的弯矩和扭矩分别为

受压夹层板的膜内力求解属于平面应力问题，由文献[9]可得

将(5)和(6)代入(1)，得径向均布压力作用下夹层圆板的横向振动方程为

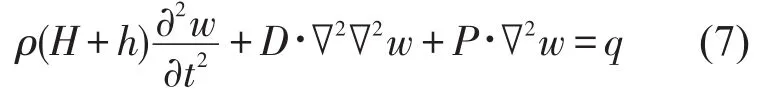
其中D为广义弯曲刚度，Ñ2为极坐标下调和算子，表达式分别为

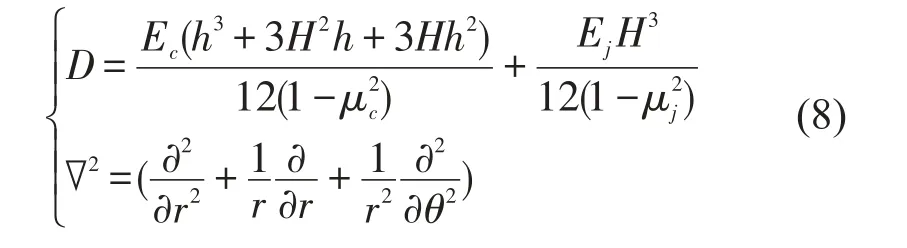
2 夹层圆板振动特性

2.1 夹层圆板固有振型

若方程(7)中q=0，即得径向均布压力作用下夹层圆板的自由振动方程。采用分离变量求解，令

将式(9)代入方程(7)，可得振型方程

式中

其中w为系统固有圆频率。

令方程(10)的解为

把式(12)代入方程(10)得

式(13)均是贝塞尔方程[10]，其解为

其中Jm(ar)、Ym(ar)、Im(ar)、Km(ar)分别为实宗量的第一类及第二类贝塞尔函数、虚宗量的第一类及第二类贝塞尔函数。

对于完整的夹层圆板，在圆心处振型为有限值。若将坐标轴置于振型对称轴上，则式(12)简化为

其中系数Am和Cm由夹层圆板的边界条件确定。

2.2 周边固支夹层圆板的固有频率

周边固支边界条件为

将式(15)代入式(16)，可得齐次线性方程组

式中

由齐次线性方程组非零解条件，得频率方程

通过求解频率方程可得其n个正根φmn，然后将φmn代入式(11)，可求出径向均布压力作用下周边固支夹层圆板的各阶固有频率

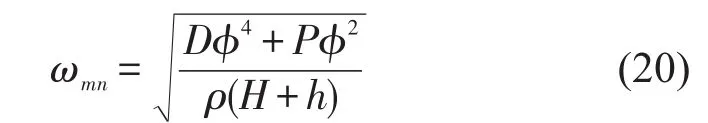
将φmn代入式(15)，可求出夹层圆板各阶振型。

3 算例

3.1 理论解的有效性验证

首先，为验证本文方法的正确性，计算了径向压力为零时夹层圆板的各阶固有频率和振型。本算例中夹层圆板的几何尺寸和材料参数数值如表1。

表2给出了各阶固有频率及其对应固有振型的理论计算结果，并与有限元结果进行了比较。表中m为节径数，n为节圆数。从表2可见，理论解与有限元结果比较接近。后文在此基础上主要讨论径向均布压力和夹层厚度参数对夹层圆板的振动特性的影响。

3.2 径向压力对固有频率的影响

图2给出了周边固支夹层圆板各阶固有频率与径向均布压力的变化关系。算例中几何参数和材料参数如表1。固有频率为零时对应的径向压力即为夹层板失稳的临界载荷。从图2可见，径向压力对夹层圆板各阶频率影响趋势相同，均表现出随径向压力增大，固有频率减小；临界载荷随阶次的增大而增大。

表1 夹层圆板的几何尺寸和材料参数

表2 周边固支夹层圆板固有频率(P=0)

3.3 夹心层比率对固有频率的影响

图2 径向压力对固有频率的影响

夹心层比率定义为夹心层厚度占夹层板总厚度的比值。图3给出了半径1.0 m、总厚度0.01 m固支夹层圆板在径向均布压力P=0和P=2 000 N/m时各阶固有频率随夹心层比率的变化。算例中材料参数见表1。从图3可见，作用径向压力时的夹层圆板各阶频率均表现出随夹心层比率增大，先缓慢增大，到峰值后减小的趋势。该趋势与无径向压力时相同；在夹心层比率一定时，有径向压力作用时夹层圆板的固有频率会比无径向压力时固有频率小。

图3 夹心层比率对固有频率的影响

4 结语

根据小挠度薄板理论，建立了径向均布压力作用下夹层圆板的振动控制方程，采用分离变量法导出了夹层圆板的固有频率及振型的理论解，讨论了径向均布载荷和夹心层厚度对固有频率的影响，得到如下结论：

(1)夹层圆板的固有频率随径向压力增大而减小；临界压力随阶次的增大而增大；

(2)作用径向压力时的夹层圆板各阶频率随夹心层比率的变化趋势与无径向压力时相同，均表现出随夹心层比率增大，先缓慢增大，到峰值后减小的趋势。

本文研究结果既可用于研究不考虑径向压力时夹层圆板的振动特性，又可用于验证其它数值解法的正确性。

[1]徐 中，石慧荣，赵 军，等.多点敷设支撑层的粘弹性约束阻尼梁振动分析[J].噪声与振动控制，2009，(1)：21-24.

[2]李 智，殷祥超，何兴华，等.复合层板减振降噪特性的数值模拟研究[J].噪声与振动控制，2006，(6)：27-30.

[3]Vinson J R.The behavior of sandwich structure of isotropic andcompositematerials[M].Lancaster:Techomic Publishing,1999.

[4]王盛春，邓兆祥，沈卫东，等.四边简支条件下正交各向异性蜂窝夹层板的固有特性分析[J].振动与冲击，2012，31(9)：73-77.

[5]杜国君.圆薄板和夹层圆板非线性振动研究[D].河北：燕山大学，2004.

[6]杜国君，胡达宇，张秀礼.静载荷作用下夹层圆板大幅度振动的时域特性分析[J].工程力学，2008，25(4)：39-44.

[7]杜国君，马建青.复合载荷下夹层圆板的非线性振动和屈曲[J].应用数学与力学，2007，28(8)：967-975.

[8]曹志远.板壳振动理论[M].北京：中国铁道出版社，1989.

[9]徐芝纶.弹性力学[M].北京：高等教育出版社，2006.

[10]吴崇试.数学物理方法（第二版）[M].北京：北京大学出版社，2003.

Analytical Solution of Free Vibration of Sandwich Circular Plate Subjected to Radial Compression

LIAO Ming-jian1,LI Ying-hui2

（1.Institute of System Engineering,CAEP,Mianyang 621999,Sichuan China; 2.School of Mechanics and Engineering,Southwest Jiaotong University,Chengdu 610031,China)

Based on the basic assumptions of elastic thin plates,the vibration control equation of a sandwich circular plate subjected to uniform radial compression is established.The analytical expressions of natural frequencies and vibration modes are derived by employing the method of separate variables.The natural frequencies and modes of a clamped sandwich circular plate are calculated.The influence of radial compression and core ratio on natural frequency is discussed.It is concluded that the natural frequency decreases with the radial compression increasing,the critical compressive force increases with the increase of orders,and the natural frequency of the plate increases at first and then decreases with the increase of core ratio.

vibration and wave;sandwich circular plate;natural frequency;uniform radial compression

1006-1355(2014)03-0011-04

O326

A

10.3969/j.issn.1006-1335.2014.03.003

夹层板结构具有质量轻、强度高、刚度大等诸多优点，在航空、航天等重要工业中应用广泛。飞行器结构中应用的夹层圆板通常既承受面力，又承受横向载荷，因此研究面力作用下夹层圆板的弯曲振动问题在飞行器设计中有重要的实际意义。目前对夹层结构的研究主要集中在振动特性、非线性振动和稳定性等方面。徐中[1]采用假设模态法研究了夹层约束阻尼梁结构的振动特性。李智等[2]采用理论模态分析技术研究了悬臂复合层板的动态特性。Vinson[3]运用经典叠层板理论研究了复合材料夹层矩形板的振动特性问题；王盛春等[4]研究了四边简支条件下正交各向异性蜂窝夹层板的固有特性；杜国君[5]利用修正迭代法讨论了夹层板参数对夹层圆板非线性振动的影响；杜国君等[6]采用假设模态法和变分法研究了均布载荷作用下夹层圆板大幅度振动时初挠度和夹层板剪切参数对其振动特性的影响；杜国君等[7]采用假设模态法和变分法研究了复合载荷下夹层圆板的非线性振动和屈曲问题。对于面内径向压力作用下夹层圆板结构的横向振动特性的研究较少。

2013-06-12

国家自然科学基金（11072204）；中央高校业务费专项（SWJTU11ZT15）；中国工程物理研究院科学技术发展基金重点资助项目（2010A0203007）

廖明建（1976-），男，重庆市合川人，硕士，从事结构振动与噪声控制研究。

E-mail:liaomj@caep.ac.cn