曲线箱梁桥的空间传递矩阵
闫仙丽,李青宁
(西安建筑科技大学土木工程学院,陕西西安710055)
曲线箱梁桥在现代桥梁建设中的应用非常广泛,其受力状况复杂,尤其在预应力作用下表现为弯扭耦合作用下的空间受力,一直以来都是众多专家学者研究的热点[1-5]。目前关于曲线箱梁桥的设计理论主要有纯扭转理论、约束扭转理论、梁格理论以及横向分布理论等,计算方法主要包括精确计算法、有限元法、梁格法等[6-7],各种理论方法都有其优缺点及适用范围。以往的研究方法主要集中于刚度法,相对刚度法而言,传递矩阵法力学概念清晰、编程方便、计算精度高,目前已有不少学者将传递矩阵法运用于曲线桥计算[8-12],如孙建鹏[13]将精细积分法与传递矩阵法相结合,推出了曲线梁桥在不同荷载情况下的精细积分公式,王福敏[14]将传递矩阵运用于曲线桥的工程实践等,但是文献[13]中传递矩阵为隐式,计算中采用精细积分法,计算复杂且耗时,文献[14]采用推导方法复杂,影响其推广应用,且二者均没有考虑箱梁剪切中心与形心可能不重合的影响,为此本文结合平衡方程、卡式定理及虚功原理推导了线弹性曲线箱梁的空间传递矩阵。
1 曲线箱梁的状态向量
如图1所示悬臂梁(计算过程中悬臂梁的固定端根据不同情况选取为i端或j端),半径为R,取单元i端局部坐标系为:原点为截面形心C,x轴为截面形心连线,y轴为截面径向形心主轴,z轴为截面竖向形心主轴。zs为剪切中心到形心轴的距离,α为曲梁的中心角,规定曲率正方向为顺时针方向。

图1 曲线箱梁计算图Fig.1 Calculation diagram of curved box-girder bridge
曲线箱梁的状态向量包括:3个方向的力、力矩及其对应的位移,写成向量形式为 S=[NVyVzTMyMzuxuyuzφxφyφz]T,其中轴力N,弯矩Mz,My作用点为形心C,剪力Vy,Vz和扭矩T作用点为剪切中心S。
悬臂梁段i、j端的状态向量关系为

式中:T为曲梁由i端到j端的传递矩阵。
2 传递矩阵T的推导
计算中假定:箱梁为弹性受力状态;由于翘曲畸变引起的内力较小,所以计算中忽略二者影响;箱梁剪切中心与截面形心位置不在同一点。
根据传递矩阵T中元素的物理意义,将矩阵分成4 部分(T1,T2,T3,T4)分别进行求解,如式(2)所示。

2.1 求解 T1
T1各项的物理意义为:当悬臂梁在i端受到节点力 Fi=[NiVyiVziTiMyiMzi]T作用时,在截面j端产生的力:
Fj=[NjVyjVzjTjMyjMzj]T
选取基本体系为j端固定的悬臂梁,由平衡条件得
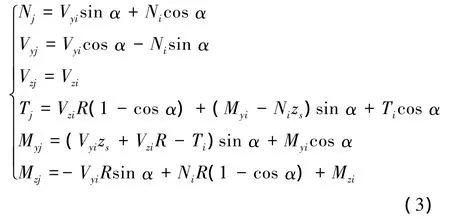
写成矩阵形式为

式中:
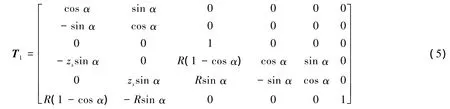
2.2 求解T2
T2各项的物理意义为:当悬臂梁在i端受到的支座位移Ui=[uxiuyiuziφxiφyiφzi]T作用时,在截面j端产生的力:
Fj=[NjVyjVzjTjMyjMzj]T即:

选取基本体系为i端固定的悬臂梁,由平衡条件得

2.3 求解 T3
T3各项的物理意义为:当悬臂梁在i端受到节点力Fi=[NiVyiVziTiMyiMzi]T的作用时,在截面j端产生的位移:
Uj=[uxjuyjuzjφxjφyjφzj]T
即:

选取基本体系为j端固定的悬臂梁,设i端受到节点力Fi作用时,梁上任一点θ处的截面内力为

曲线梁的应变能为
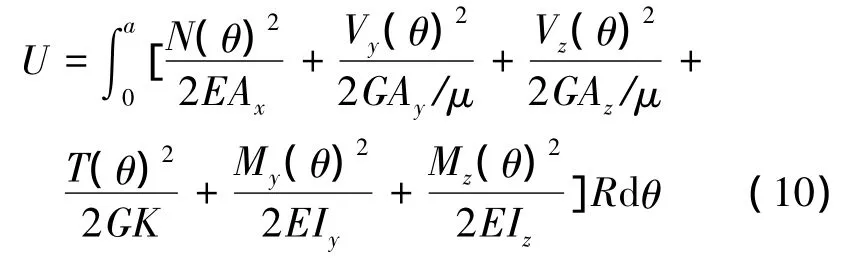
式中:Ay、Az、Ax分别为箱梁y、z方向的剪切面积、截面积;Ⅰy、Ⅰz、K为箱梁y、z轴方向的截面惯性矩、截面扭转常数;μ为剪切系数。
由卡氏原理求出T3中各元素:
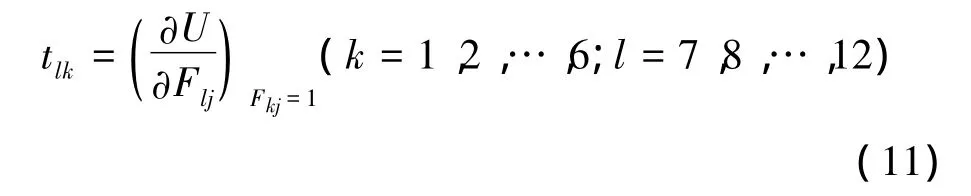
计算得到

式中:


2.4 求解 T4
T4各项的物理意义为:当悬臂梁在i端有支座位移 Ui=[uxiuyiuziφxiφyiφzi]T作用时,在截面j端产生的位移:
Uj=[uxjuyjuzjφxjφyjφzj]T即:

选取计算基本体系为i端固定的悬臂梁,令i端分别发生各个方向的单位支座位移uli时,求j端产生的相应位移值tjk。根据虚功原理,采用单位力法,因在静定结构中,支座位移不产生内力,因此虚功原理表达式简化为

式中:tjk为i端位移值,uli为i端支座位移(分别取uxi、uyi、uzi、φxi、φyi、φzi);Ril为i端支座反力。
计算结果如下:


3 外荷载作用下的传递矩阵
3.1 基本概念及求解方法
考虑外荷载作用时,为使计算简单,将外荷载项引入传递矩阵内部,在单元传递关系中,增加一个恒等式1≡1。
定义梁上任意点的状态矢量为 S=[NVyVzTMyMzuxuyuzφxφyφz1]T,则单元两端传递关系为
式中:T=为13×13矩阵,表示包含外荷载项的曲梁单元由i端到j端的传递矩阵;pt1,p-p t12,p为外荷载p引起的内力和变形,根据外荷载的不同类型,p取为qz、Pz、Mx等。
定义:


式中:SPF为外荷载p引起的力向量,SPδ为外荷载p引起的位移向量。
将外荷载分别单独作用于单元基本计算体系,求解单元的外荷载向量。
3.1.1 SPF求解
SPF各项的物理意义为:当悬臂梁在单独单位外荷载下作用时,在截面j端产生的力 Fj={NjVyjVzjTjMyjMzj}T,选取基本体系为j端固定的悬臂梁,由平衡条件得
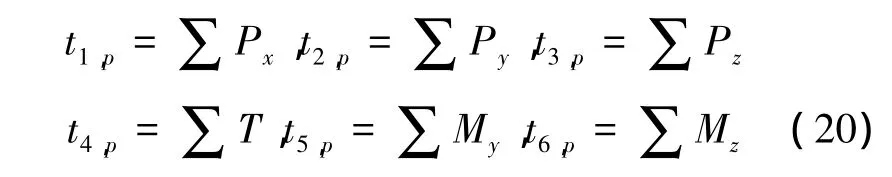
式中:Px、Py、Pz、T、My、Mz分别为荷载的x向、y向、z向分量及其对j端的力矩。
3.1.2 SPδ求解
SP各项的物理意义为:当悬臂梁在单独单位外δ荷载下作用时,在截面j端产生的位移 Uj=[uxjuyjuzjφxjφyjφzj]T。选取计算基本体系为j端固定的悬臂梁,参照T3求解过程,将节点力换为外荷载,由卡式定理求解。
3.2 均布竖向荷载qz作用下外荷载项的求解
如图2所示,均布竖向荷载qz作用下,由平衡条件和卡式定理得:单元j端的外荷载向量为
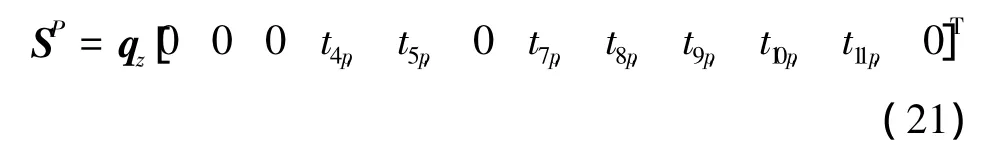
式中:
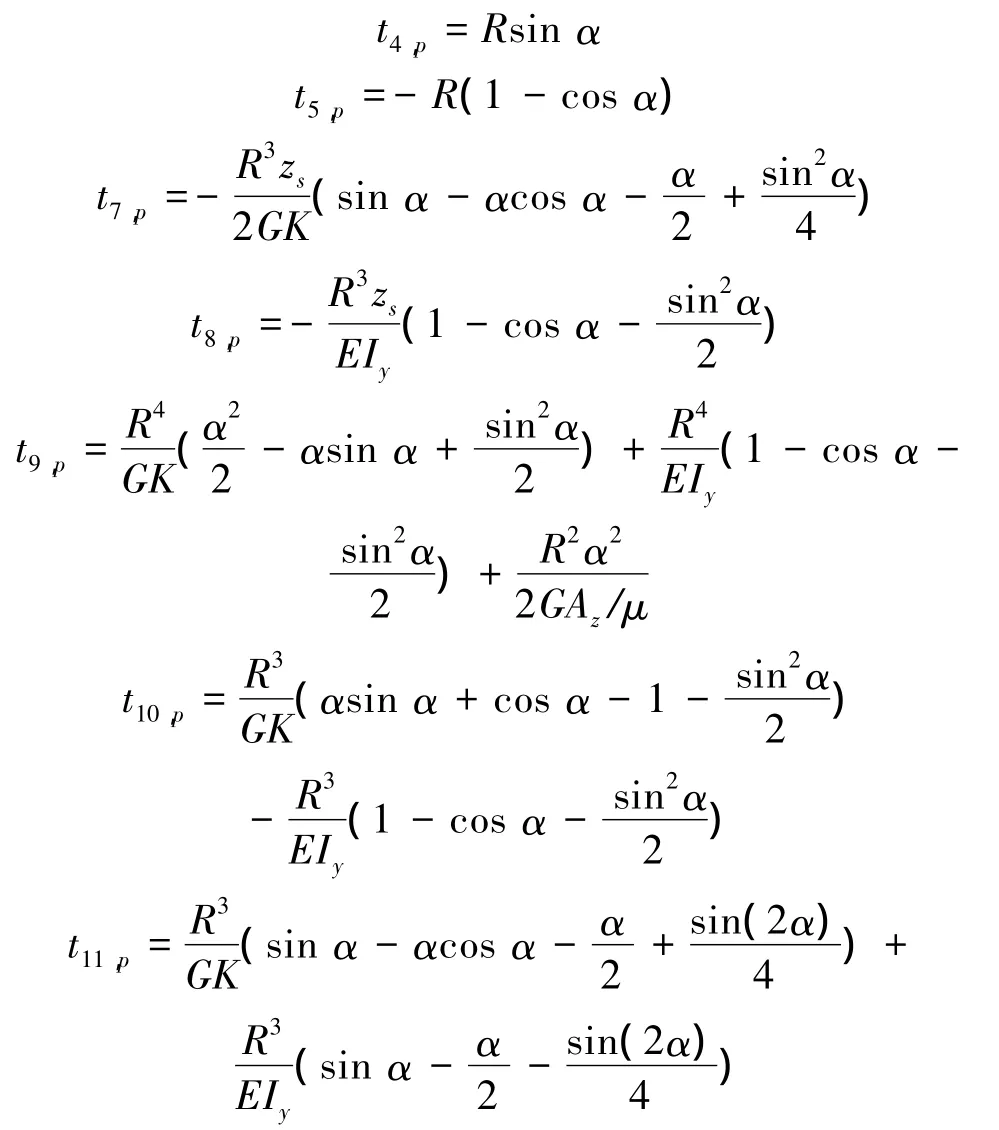

图2 均布竖向荷载qzFig.2 Vertical uniformly distributed load qz
3.3 集中竖向荷载Pz作用下外荷载项的求解
如图3所示,Pz作用下,由平衡条件和卡式定理得:单元j端的外荷载向量为
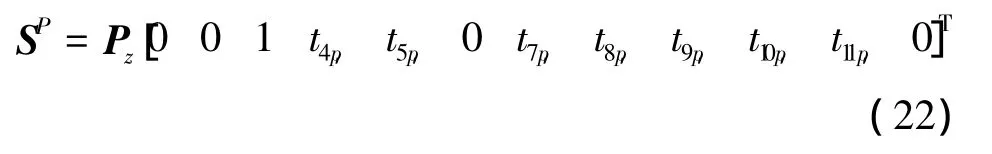
式中:

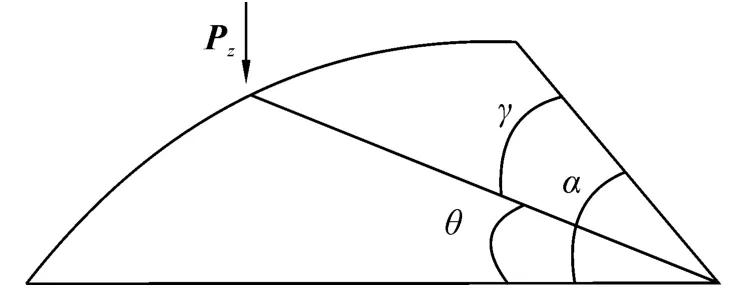
图3 集中竖向荷载PzFig.3 Vertical concentrated load Pz
3.4 集中扭转荷载Mx作用下外荷载项的求解
如图4所示,Mx作用下,由平衡条件和卡式定理得:单元j端的外荷载向量为

式中:



图4 集中扭转荷载MxFig.4 Concentrated torsional load Mx
4 计算实例
为了验证公式的正确性,采用模型试验梁示例。如图5所示单跨曲线箱梁桥,桥长30 m,梁宽8 m,曲线半径R=30 m,圆心角为57°,单箱单室截面,所受荷载为沿全桥的均布荷载100 kN/m,集中竖向力280 kN,集中竖向扭矩1 000 kN·m,求截面内力。

图5 桥梁计算简图及截面尺寸(cm)Fig.5 Bridge calculation diagram and section size(cm)
将该桥梁平均分为8段(节点编号顺序如图5),定义任意截面的状态矢量为 Sk=[NVyVzTMyMzuxuyuzφxφyφz1]Tk(k=1,2,…,9),则每段梁的传递关系为
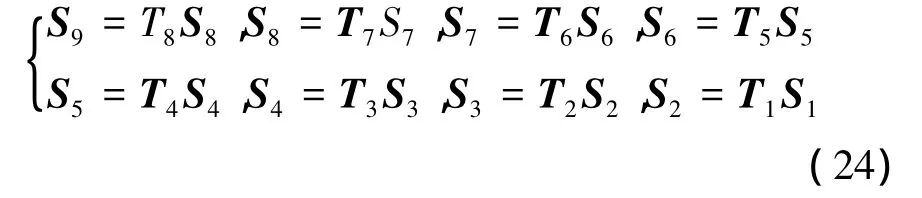
式中:Tk=为各段梁单元的传递矩阵。
T1,3,4,5,6,7中 ,pt1,p,pt2,p,…,pt12,p为均布荷载下SPqz中相应数值,即pti,p=qztqz i,p,式中 α=7.125°;
T2中,pt1,p,pt2,p,…,pt12,p为均布荷载SPqz和集中荷载SPFz下中相应数值的和,即pti,p=,式中:α=7.125°,θ=0°,γ=7.125°;
T8中,pt1,p,pt2,p,…,pt12,p为均布荷载SPqz和集中扭转荷载SPMx下中相应数值的和,即pti,p,式中 α =7.125°,θ=0°,γ =7.125°。
结构整体传递方程为

将边界条件:
S1=[NVyVzT0 0 0 0 0 0 φyφz1]1T
S9=[0VyVzT0 0ux0 0 0 φyφz1]9T
代入式(25)得到边界条件中的未知参数,然后代入每段梁的传递矩阵式(24),得到所有截面的状态矢量。
将上述传递过程采用Matlab软件进行编程计算,得到结果如表1所示。
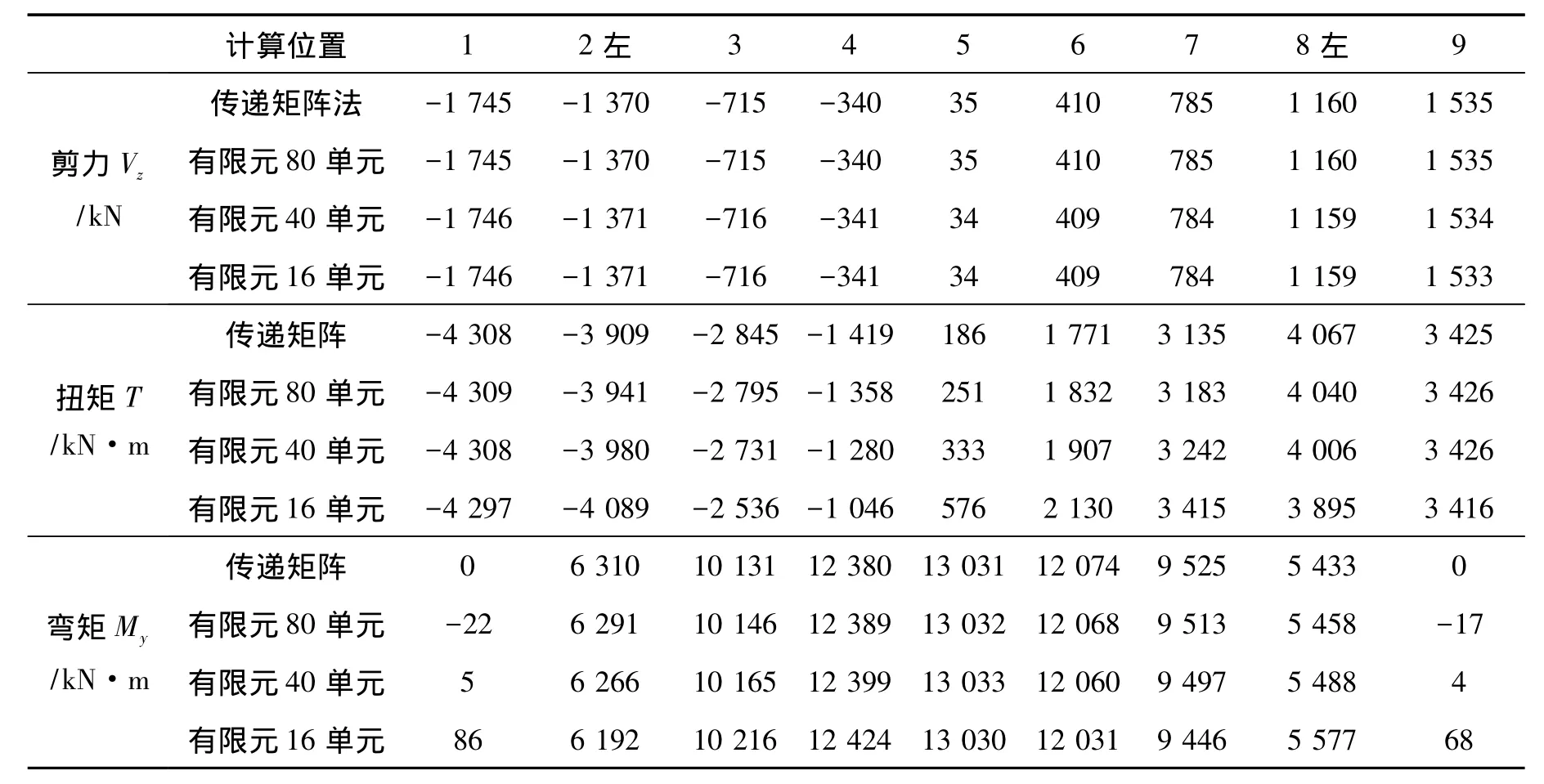
表1 传递矩阵法(TMM)与有限元法(FEM)计算的桥梁内力值Table 1 Internal force of the model bridge calculated by TMM and FEM
为与传递矩阵法相比较,将该曲线梁桥采用有限元软件Midas进行建模分析,采用“以直代曲”法,将全桥划分为16,40,80个直梁单元分别进行建模分析,其计算结果如表1。
对比表1有限元软件Midas与本文传递矩阵公式法计算得到的内力结果,可看出2种方法计算结果基本吻合,有限元分析中,随着单元划分数量增加,其结果越来越接近于传递矩阵法计算结果,说明相比于有限元法,传递矩阵公式法更为精确,划分8个单元的精度便可高于有限元法80个单元的结果,原因在于本文推导传递矩阵公式均为解析解。
4 结论
1)本文推导了曲线箱梁桥的空间传递矩阵公式,针对实例进行了编程运算,与有限元法计算结果进行对比,二者结果基本吻合,说明该公式是有效的,本文推导方法可行。
2)通过对不同单元划分情况下的有限元分析结果与传递矩阵法分析结果进行对比可得出,本文传递矩阵公式法因其为精确解析解,计算结果比“以直代曲”有限元法法更为精确,划分较少单元却能达到很高的精度,计算效率提高。
3)由于本文推导公式均为显式,且为精确解,在简单荷载情况下,手算也可实现。可用于工程及学习中的计算及检验。
4)从本文推导过程可看出,与传统初参数法相比较,本文推导方法概念清晰,计算简单,可推广应用于其他结构在各种不同荷载情况下传递矩阵公式的推导。
[1]QIAO J L,JIN Y,TIAN W L,et al.The shear-lag effect on curved box girder bridge considering prestress and initial curvature[J].Applied Mechanics and Materials,2012,204:2100-2104.
[2]TAYI N,ÖZAKC A M.Free vibration analysis and shape optimization of box-girder bridges in straight and curved planform[J].Engineering Structures,2002,24(5):625-637.
[3]CHANDRA MOHAN RAO B D V,RAMANA RAO N V.A-nalysis and optimization of box girder bridges in curved planform[J].Journal of The Institution of Engineers(India):Series A,2012,93(1):1-8.
[4]GOMEZ H C,FANNING P J,FENG M Q,et al.Testing and long-term monitoring of a curved concrete box girder bridge[J].Engineering Structures,2011,33(10):2861-2869.
[5]赵青,肖卓.行波效应对连续曲线箱梁桥地震反应的影响[J].地震工程与工程振动,2010,3:123-128.ZHAO Qing,XIAO Zhuo.Effects of traveling wave on seismic responses of continuous curved box-girders bridge[J].Journal of Earthquake Engineering and Engineering Vibration,2010,3:123-128.
[6]邵容光,夏淦.混凝土弯梁桥[M].北京:人民交通出版社,1994:71-74.SHAO Rongguang,XIA Gan.Curved concrete beam bridge[M].Beijing:China Communications Press,1994:71-74.
[7]田秀兰,陈伏立.曲线梁桥设计理论述评[J].福建建筑,2005(1):368-370.TIAN Xiulan,CHEN Fuli.Commentary of the curved bridge design theory[J].Fujian Architecture and Construction,2005(1):368-370.
[8]常连生,刘衍平.求解连续梁弯曲的传递矩阵法[J].现代电力,1998,4:74-79.CHANG Liansheng,LIU Yanping.Transfer matrix method to solve the curved continuous beams[J].Modern Electric Power,1998,4:74-79.
[9]李惠生.用传递矩阵法计算弯梁的内力和变形[J].桥梁建设,1991,1(3):65-66.LI Huisheng.Internal force and deformation calculations of the curved beams with the transfer matrix method[J].Bridge Construction,1991,1(3):65-66.
[10]瞿尔仁,王建立.传递矩阵法在曲线桥结构分析中的应用[J].合肥工业大学学报:自然科学版,1999,22(6):73-79.QU Erren,WANG Jianli.Transfer matrix method applied to structural analysis of curve bridge[J].Journal of Hefei University of Technology:Natural Science,1999,22(6):73-79.
[11]项贻强,金海明.铰接曲板桥传递矩阵法的计算[J].华东公路,1991,73(6):53-58.XIANG Yiqiang,JIN Haiming.Calculations of the articulated curved slab-bridge by transfer matrix method[J].East China Highway,1991,73(6):53-58.
[12]何云勇.一种分析曲线箱梁剪力滞效应的传递矩阵法[J].重庆交通大学学报:自然科学版,2010,29(5):670-673.HE Yunyong.Transfer matrix method for analyzing shear lag effect of curved box girder bridge[J].Journal of Chongqing Jiaotong University:Natural Sciences,2010,29(5):670-673.
[13]孙建鹏.曲线箱梁桥状态传递理论研究[D].西安:西安建筑科技大学,2010:48-57.SUN Jianpen.Study on state transfer theory of curved box bridge[D].Xi'an:Xi'an University of Architecture and Technology,2010:48-57.
[14]王福敏.曲线梁桥传递矩阵设计法与工程应用实践[M].北京:人民交通出版社,2009:1-34.WANG Fumin.Transfer matrix design method of the curved girder and its engineering application[M].Beijing:China Communications Press,2009:1-34.

