舰载风速仪测量误差与安装位置的关系研究
郜冶,谭大力,李海旭,王金玲,刘长猛
(1.哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001;2.海军装备研究院,北京100192;3.中国船舶工业系统工程研究院,北京100094)
大型水面舰船的机动性对军事战术的实施尤其对舰载机的起飞降落过程起着决定性作用,这就要求舰船在航行过程中必须确定相对于优势风的正确航向和特定的前进速度,确保舰载机安全着舰[1]。目前大型舰船主要依靠安装在船桥中央桅杆上的测风仪器测量风速,风速仪本身的测量精度符合要求,但由于受舰船甲板及其舰上岛型建筑周围涡流的影响安装在涡流区的风速仪测得的风场与实际真风存在很大的误差。在国外,M.L.Thiebaux利用风洞试验研究了舰载风速仪的误差校正问题[2];P.K.Taylor和 E.C.Kent等针对商用船,利用实验和CFD方法研究了受船体影响其周围风场产生的扭曲和变形对风速仪测量精度的影响,并与卫星测报数据进行了对比[3-4];Philippe L.Nacass采用 CFD计算船载风速仪周围的气流失真现象[5]。在国内,刘连吉等用实验方法研究了船上风速仪测量风速与浮标测量风速的误差,并提出了测量风速的改进意见[6-7];刘慧等将船测风场资料与QuikSCAT卫星遥感风场资料进行对比分析研究了船测风场偏差统计特征[8]。近年来郜冶等致力于舰船流场的CFD计算,文献[9]中运用CFD计算空气正向流过滑跃式舰船产生的甲板气流场,讨论分析不同网格划分形式对计算结果的影响,通过对全尺寸的滑跃式甲板舰船的数值计算分析得到舰船甲板气流场涡旋结构特征,并将不同湍流模型应用于流场计算,分析了舰船流场的特点。文献[10]利用FLUENT软件UDF接口将LK和MMK模型引入FLUENT进行流场计算改进了计算结果。
本文采用数值模拟方法对不同工况下风速仪周围的气流场进行计算分析,得出风速仪更加合适的安装位置。如计算条件允许,理论上可以研究流体在任何条件下的运动,再现风速仪周围的风场。
1 数值模拟物理模型与数学描述
1.1 物理模型
为便于计算,将风速仪安装位置处物理模型(包括梯形柱台、雷达、天线和其他附属结构)进行合理简化,忽略掉不影响流场特征的细微结构如毫米级的天线、柱台上的小孔等,简化后的模型如图1所示。
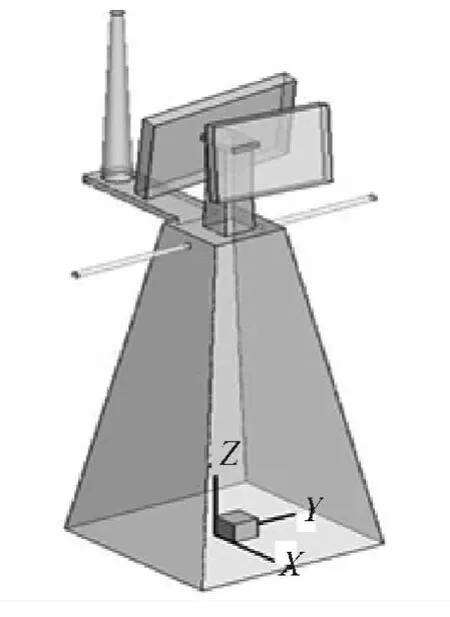
图1 计算模型Fig.1 The calculation model
计算区域X轴表示船长方向,由船头指向船尾为正方向,Y轴表示船宽方向,由左舷指向右舷为正方向,Z轴表示竖直方向,由下方指向上方为正方向,模型关于中心位置左右对称。坐标原点位于梯形柱体底部中心处,现有方案风速仪安装在如图2中所示监测点位置,其坐标分别为D(0.0 m,-3.68 m,13.23 m)、D'(0.0 m,3.68 m,13.23 m)。
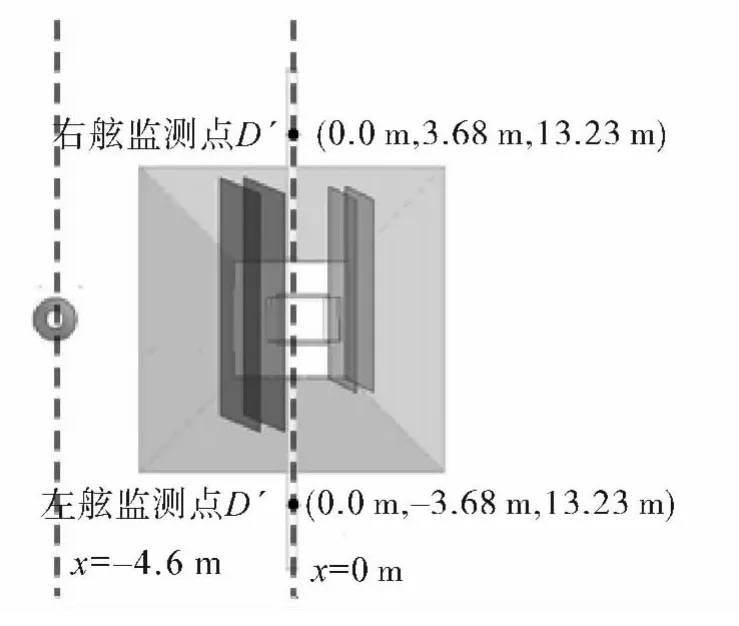
图2 风速仪监测点位置俯视图Fig.2 The location of the anemometers in the top viewport
1.2 数学模型
舰船及其风速仪周围的流场属于三维复杂湍流场,为简化计算设空气为不可压缩流体且符合Boussinesq假设,流动为稳态紊流,忽略固体壁面间的热辐射。采用标准k-ε两方程模型对气流场进行数值模拟。建立流场稳定后的湍流控制通用方程[11-12]:
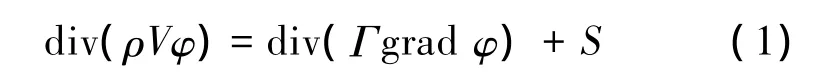
式中:div(ρVφ)表示对流项,div(Γgrad φ)表示扩散顶,S表示源项。控制方程包括连续方程如式(2)、动量方程如式(3)、能量方程如式(4)、k方程如式(5)和ε方程如式(6)。
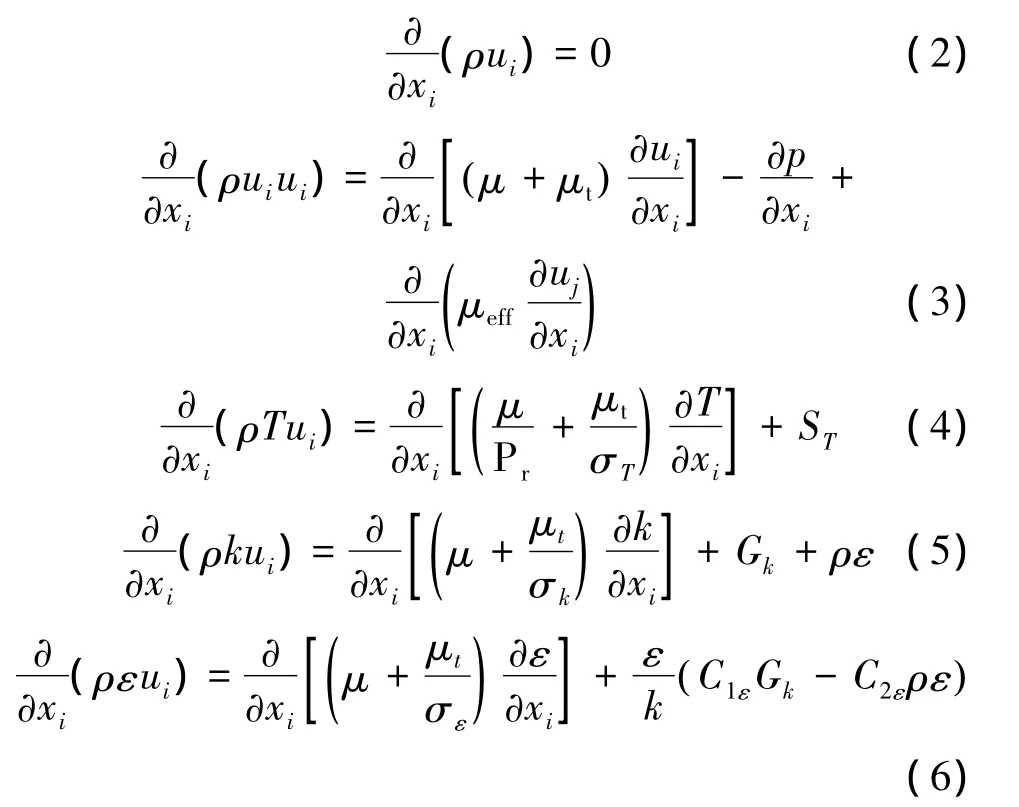
式中:Gk是由平均速度梯度引起的湍动能k的产生项,μ是湍动粘度,可表示t成湍动能k和耗散率 ε 的函数,即 μt=ρCμk2/ε;C1ε、C2ε为经验常数;σk、σε分别是湍动能k和耗散率ε对应的Prandtl数。在数值模拟过程中,各系数取为Cμ=0.09,C1ε=1.44,C2ε=1.92,σk=1.0,σε=1.3,σT=0.9。
2 网格划分及边界条件
2.1 网格划分
流场计算区域取风速仪前为10倍柱台底面边长(柱台底面边长为5.75 m),风速仪后为20倍柱台底面边长,左右均为5倍柱台底面边长,垂向为5倍柱台底面边长,基于柱台底面边长为特征尺度的雷诺数量级为1.0×107。由于计算模型比较复杂采用非结构网格,对梯形柱台、雷达、天线及附属结构区域进行网格加密。全部网格由ANSYS ICEM生成,网格总数为8.77×106,计算区域及全流场网格如图3所示,局部网格加密如图4所示。
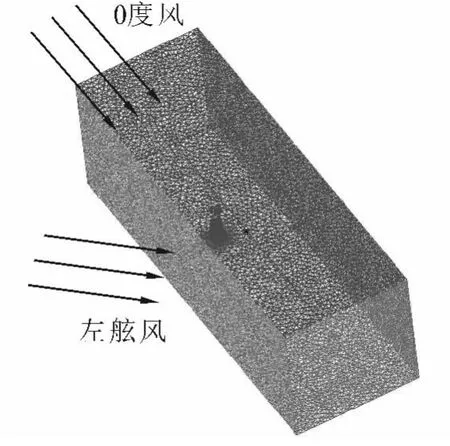
图3 计算区域及全流场整体网格Fig.3 The calculation region and grids for the whole flow field

图4 局部网格加密Fig.4 The refinement of local grid
2.2 边界条件
计算中入口设为速度入口(具体速度方向大小随不同计算工况改变),梯形柱体、雷达、天线及附属结构所有表面均设定为无滑移壁面,其余边界均设为自由滑移壁面,出口设为压力出口。
3 数值计算与结果分析
3.1 CFD计算方法验证
采用文献[11]中的方法验证CFD计算方法的准确性,将相同计算方法及网格划分方法的美国LHA级舰船的CFD计算结果与文献[15]中的风洞实验结果进行对比分析。LHA模型为1/48缩比模型,全长为 5.2 m,甲板宽为 0.75 m,网格数量约为 2.0×106,U0=6.858 m/s,使用标准k-ε 模型进行计算。验证计算中,着舰点位置如图5中所示。
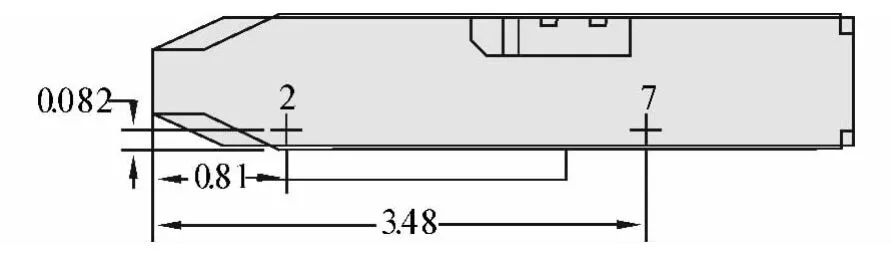
图5LHA着舰点的位置(m)Fig.5 The touchdown points of LHA(m)
图6为CFD计算结果与文献[15]中风洞试验V-22旋翼通过舰点2的倾斜轨道上垂向速度对比。横坐标为坐标值与甲板宽度d的比值,纵坐标为Z向速度W与入口速度U0的比值。图6中数据对比显示CFD计算结果与风洞试验数据吻合较好,误差不超过7%。证明论文中运用的网格划分方法及标准k-ε模型可以用于预测船体绕流场的特征。
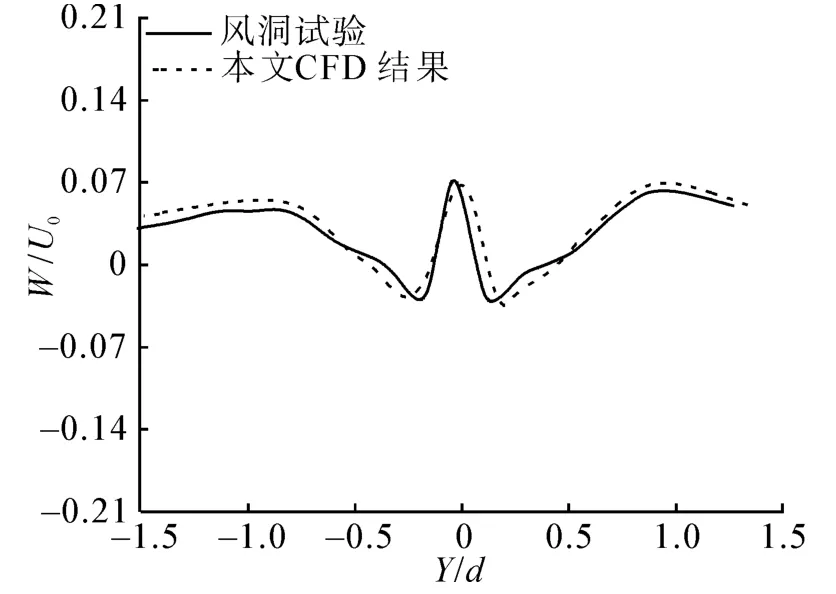
图6 着舰点2倾斜轨道上垂向速度对比Fig.6 The vertical velocity of inclined orbit comparison at touchdown point 2
3.2 现有风速仪安装方案流场计算及数据分析
为讨论不同船速、风速及不同风向角对风速仪测量位置处流场的影响,对现有安装方案设置3种工况进行对比,当船速3 m/s,风速3 m/s(低航速低风速)时记为工况A;当船速14 m/s,风速3 m/s(高航速低风速)时记为工况 B;当船速14 m/s,风速14 m/s(高航速高风速)时记为工况C。并对每种工况设置4种不同的风向角进行计算,图3中给出了风向角示意表示,从船体正前方吹风时设为是0°风,从船体左舷吹风时设是左舷风,由于模型关于中心位置左右对称,因此只计算左舷风。计算时风向角分别选取 0°、10°、20°、30°。将每种工况左右监测点D、D'处数据进行提取,分离出此处风向角α'及风速υ',并与无穷远处真风风向角α及风速υ进行对比,得到风向角差值 Δα和风速差值的模,其计算方法如图7所示。现定义风向角差值Δα方向:与实际真风相比,监测点真风逆时针偏转为正,顺时针偏转为负。
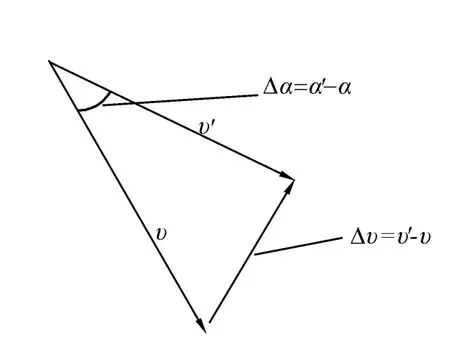
图7 风向角差值和风速差值计算示意图Fig.7 The calculation schematic diagram for wind angle and vector difference
图8和图9分别为工况A、B、C在不同风向角α时α'及e(υ')计算结果,其中e(υ')表示风速值误差。风速仪在现有安装位置得到的α'及e(υ')均较大,其中工况A与工况C误差相差不大,而工况B中α'及e(υ')远远高于工况A和工况C,即低风速高船速时风速仪的测量误差急剧升高;随α值增大,各工况近风侧D测点(左舷测点)α'误差逐渐减小,远风侧D'测点(右舷测点)α'误差逐渐增大,且远风侧误差明显小于近风侧误差;但随风向角α增大,工况B及工况C中风速值误差e(υ')减小,工况A在α=30°时风速值误差e(υ')明显增大,且远风侧风速值误差始终略大于近风侧误差。
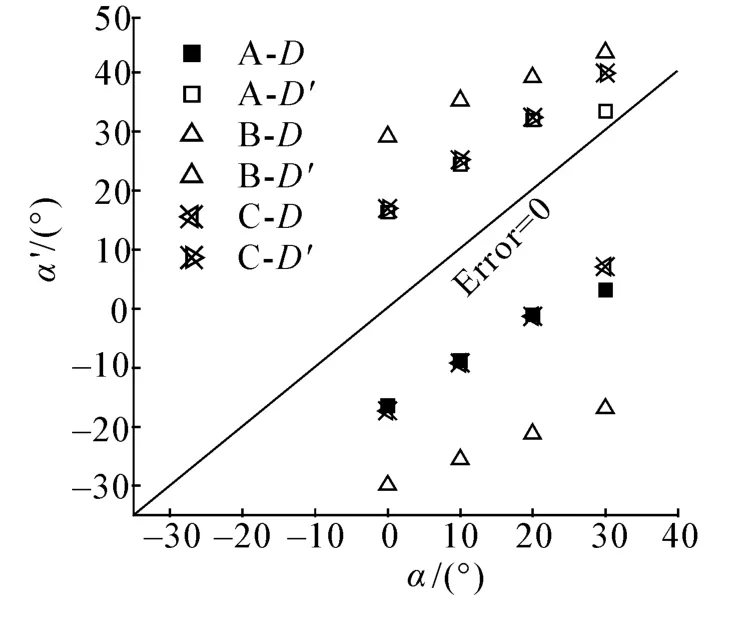
图8 3种工况不同位置处α'计算结果Fig.8 The calculation result α'for the 3 conditions
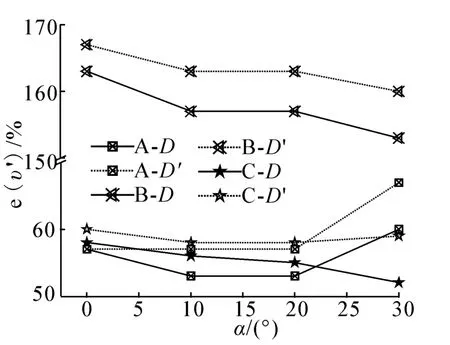
图9 3种工况不同位置风速值误差计算结果Fig.9 The wind speed error for the 3 conditions
3.3 风速仪其他安装方案流场计算及数据分析
鉴于风速仪在现有安装位置风向角及风速值测量误差均较大,特设置风速仪不同安装位置进行计算,试图找到更合适的安装位置以减小测量误差。
不改变风速仪安装高度,分别令x为0 m、-4.6 m 时,y为±3、±4、±5、±6、±7,±8 m,即将风速仪安装位置在x=0 m与z=13.23 m及x=-4.6 m与z=13.23 m交线上分别由内向外进行平移。风速仪监测点分布线如图2中所示。
3种工况都分别对α为0°和30°时,风速仪安装在不同测点时的流场风速进行计算。图10和11分别为3种工况在不同风向角α值时不同测点的α'计算结果,图12和13分别为3种工况在不同风向角α值时不同测点的风速值误差e(υ')。
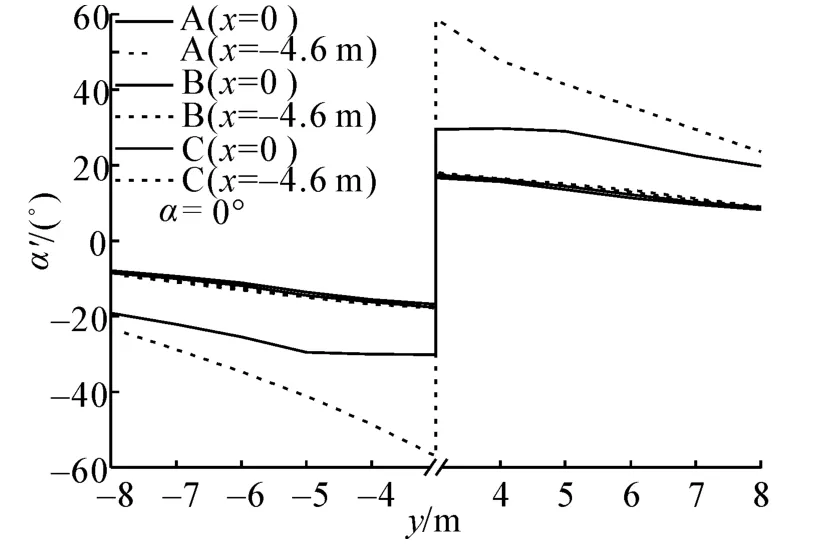
图10 α为0°时3种工况不同位置处α'计算结果Fig.10 α'calculation result for the 3 conditions in 0°
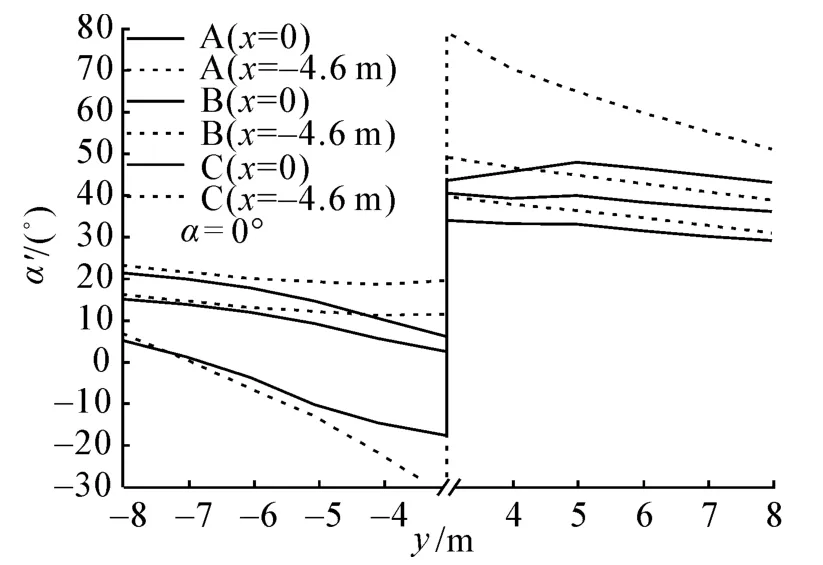
图11 α为30°时3种工况不同位置处α'计算结果Fig.11 α'calculation result for the 3 conditions in 30°
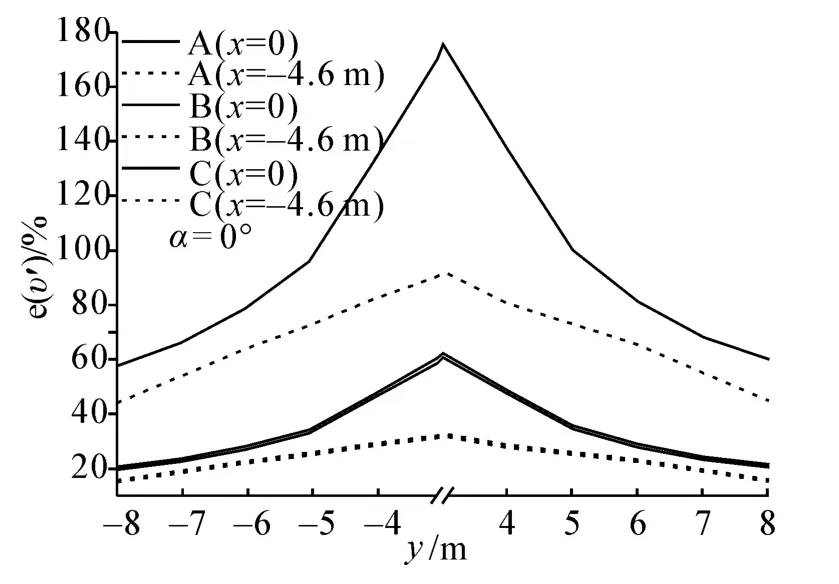
图12 α为0°时3种工况不同位置风速值误差计算结果Fig.12 Wind speed error for the 3 conditions in 0°
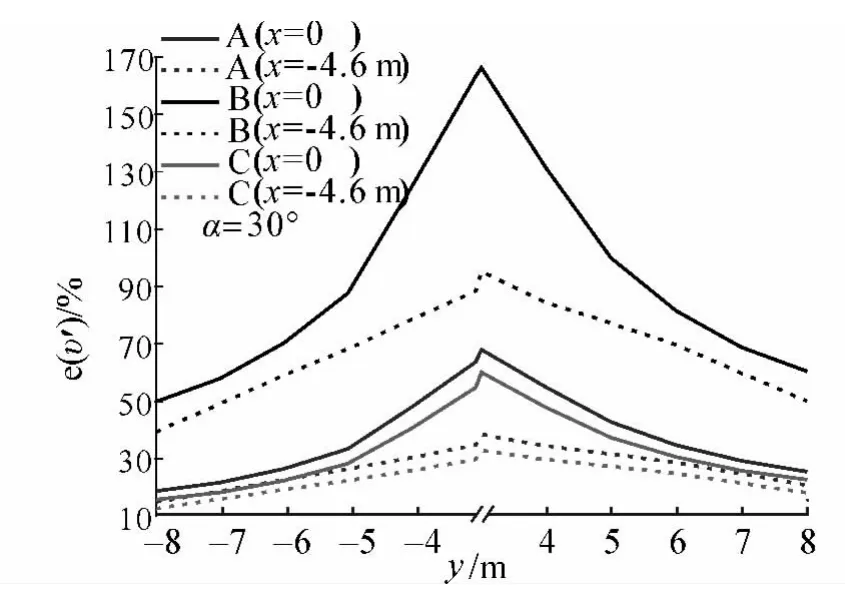
图13 α为30°时3种工况不同位置风速值误差计算结果Fig.13 Wind speed error for the 3 conditions in 30°
计算结果显示随着风速仪安装位置由内向外移动,风向角α'及风速值误差e(υ')均随y值绝对值(风速仪监测点距中心的距离)增大而减小,即将风速仪安装位置向外移动有助于减小测量误差。在远风侧,3种工况x=-4.6 m处的α'误差普遍略大于x=0处,且随α增大2位置处的α'差距加大。在近风侧,工况A和C在x=-4.6 m处的α'误差小于x=0处,且随风向角α增大两位置处的α'差距加大;而工况B在x=-4.6 m处的风向角α'误差略大于x=0 m处,且随风向角α增大两位置处的α'差距减小。对于风速值,3种工况在x=-4.6m处误差均明显小于x=0处,且随风向角增大两位置处风速值误差差距加大。即将风速仪安装位置向前移到天线位置处可以明显减小风速值测量误差且风向角测量误差不会显著增大。
3.4 船体结构对流场影响
以上计算中仅考虑风速仪安装位置的物理模型,忽略了船体结构的影响。为讨论船体结构对风速仪测量位置处流场结构的影响,将船体模型和风速仪模型合并,如图14所示。当船速为0,风速为5 m/s时为工况D,当船速为0,风速为20 m/s时为工况E,且分别对风速仪模型及合并模型进行计算。工况D对风向角为0°,工况E对风向角为0°和30°时,风速仪不同测点的流场进行计算。
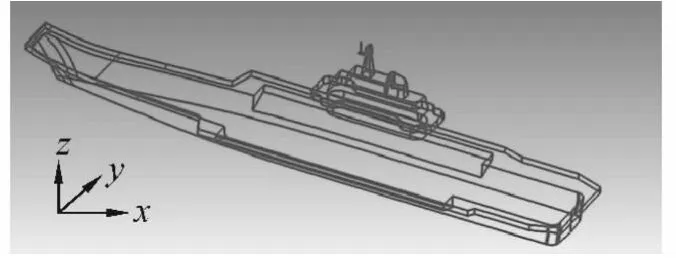
图14 船体和风速仪合并模型Fig.14 The merge model of ship and anemoscope
图15~20分别为工况D、E风向角及风速值误差计算结果。计算结果显示2种工况风速仪单独模型与合并模型测量误差随y值的变化趋势是相同的,随风速仪安装位置向外延伸两模型的风向角及风速值测量误差差距均减小。
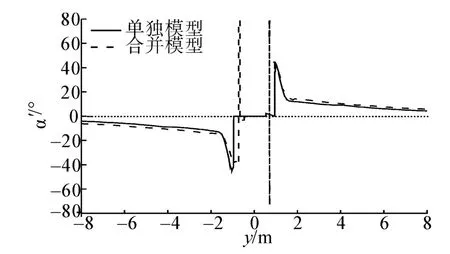
图15 α为0°时工况D风向角差值α'计算结果Fig.15 α'calculation results for condition D in 0°
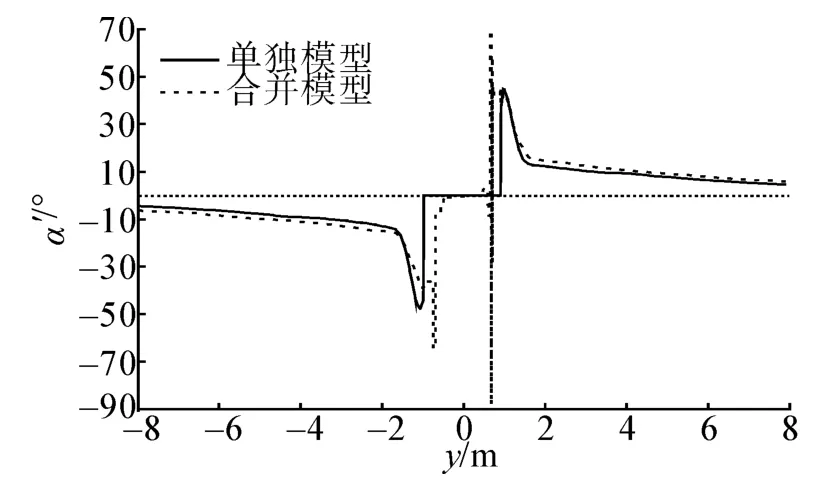
图16 α为0°时工况E风向角差值α'计算结果Fig.16 α'calculation results for condition E in 0°
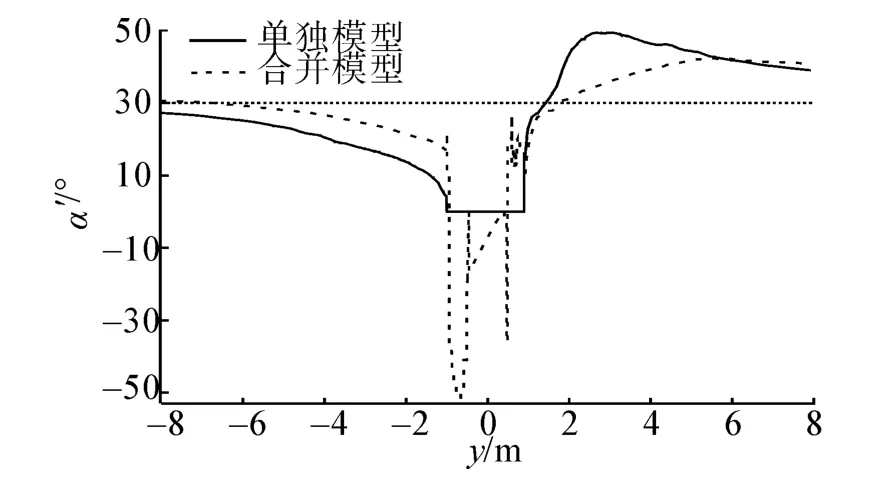
图17 α为30°时工况E风向角差值α'计算结果Fig.17 α'calculation results for condition E in 30°
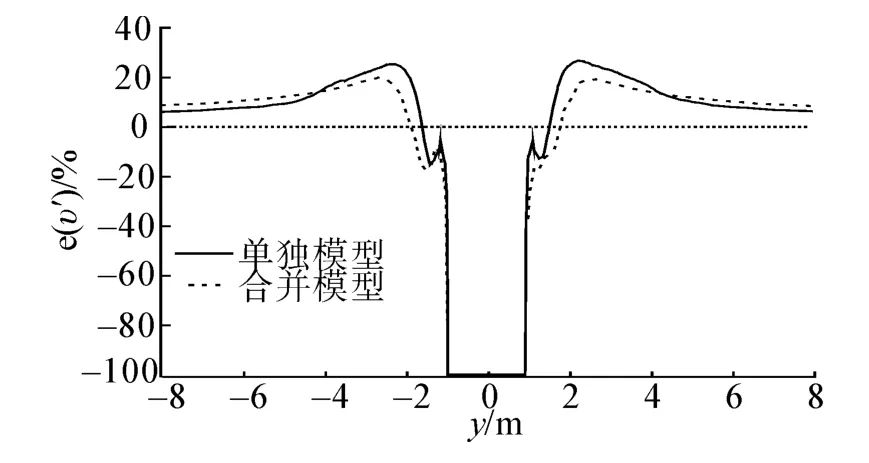
图18 α为0°时工况D风速值误差计算结果Fig.18 e(υ')calculation results for condition D in 0°
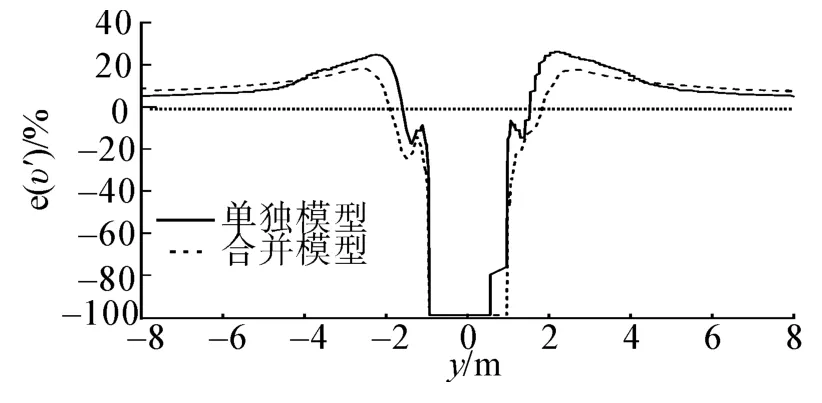
图19 α为0°时工况E风速值误差计算结果Fig.19 e(υ')calculation results for condition E in 0°
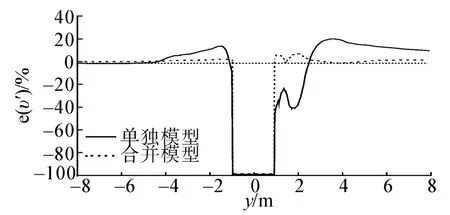
图20 α为30°时工况E风速值误差计算结果Fig.20 e(υ')calculation results for condition E in 30°
α=0°时,距离中心位置3 m以外,在左右舷对称位置2种模型测得的风向角α'数值基本相等但方向相反,且2种模型测量结果的差值基本维持在2°以内;对于风速值测量误差,在距离中心位置1~4 m,风速仪单独模型测量结果明显大于合并模型的测量结果,在距离中心位置4 m以外,合并模型测量的风速值误差略微大于风速仪单独模型的测量结果但两模型的测量误差在3%以内。
α=30°时,远风侧的风向角及风速值误差测量结果均大于近风侧的测量结果,近风侧在4 m以外两模型风向角测量值的差值在5°以内,风速值误差的差值在2%以内,而在远风侧,2种模型的测量误差差距相对较大。
4 结论
1)风速仪在现有安装位置测量误差较大,其中低风速高船速时风速仪的测量误差急剧升高。
2)随吹风角度增大,近风侧风向角测量误差逐渐减小,远风侧风向角测量误差逐渐增大,且远风侧风向角测量误差明显小于近风侧风向角测量误差。
3)随吹风角度增大,风速值测量误差变化不大,且远风侧风速值测量误差始终略大于近风侧风速值测量误差。
4)将风速仪安装位置向外平移有利于减小风向角和风速值测量误差;将风速仪安装位置向前移到天线位置处可以明显减小风速值测量误差且风向角测量误差不会显著增大。
5)船体本身会对风速仪附近的流场产生较大的影响。在此区域内,合并模型风速仪测量精度明显较风速仪单独模型低,随风速仪安装位置外移,2种模型的测量差距减小,尤其在近风侧2种模型的测结果基本相同。此时可以使用风速仪单独模型代替合并模型进行定性分析,但是定量分析时应该使用合并模型。
[1]宋剑,何建忠.航空母舰在随机海况下的运动统计特性[J].舰船电子工程,2011,31(3):67-69.SONG Jian,HE Jianzhong.Statistical properties of the movement of aircraft carrier in the random sea conditions[J].Ship Electronic Engineering,2011,31(3):67-69.
[2]THIEBAUX M L.Wind tunnel experiments to determine correction functions for shipborne anemometers[J].Hydrog and Ocean Sci,1990,36(2):57-61.
[3]TAYLOR P K,KENT E C,YELLAND M J,et al.The accuracy of wind observations from ships[J].Advances in the Applications of Marine Climatology,1995,2(2):132-155.
[4]TAYLOR P K,KENT E C.The accuracy of meteorological observations from voluntary observing ships-present status and future requirements[C]//WMO,First Session of the CMM Subgroup on Voluntary Observing Ships.Athen,Geneva,1999:12.
[5]PHILIPPE L N.Shipborne wind measurements corrected for airflow distortion by computational fluid dynamics[R]//Brétigny-sur-Orge:Centred'Aviation Météorologique,2001:228-233.
[6]刘连吉,赵永平.船上气温、湿度和风速观测的代表性[J].山东海洋学院学报,1981,11(3):24-31.LIU Lianji,ZHAO Yongping.The reliability of the wind speed air temperature and humidity observed on ship[J].Journal of Shandong College of Oceanology,1981,11(3):24-31.
[7]刘连吉.对现用海洋水文气象要素调查规范的改进意见[J].海洋技术,1982,1(2):70-73.LIU Lianji.Suggestions on the instruction manual for obtaining oceanographic and meteorological data[J].Acta Oceanologica Sinica,1982,1(2):70-73.
[8]刘慧,胡松,邹晓荣.船测资料与智利外海QuikSCAT风场比较分析[J].遥感技术与应用,2012,27(5):763-769.LIU Hui,HU Song,ZOU Xiaorong.Comparison between the fishing vessels and QuikSCAT scatterometer wind data of the offshore Chile[J].Remote Sensing Technology and Application,2012,27(5):763-769.
[9]刘长猛,郜冶.滑跃式甲板气流场数值模拟[J].华中科技大学学报,2012,40(10):68-71.LIU Changmeng,GAO Ye.Numerical simulation of airwake on ski jump deck[J].Journal of Huazhong University of Science and Technology,2012,40(10):68-71.
[10]郜冶,刘长猛.护卫舰气流场数值计算研究[J].哈尔滨工程大学学报,2013,34(1):1-5.GAO Ye,LIU Changmeng.Numerical simulation of frigate ship airwake[J].Journal of Harbin Engineering University,2013,34(1):1-5.
[11]LAUNDER B E,SPALDING D B.The numerical computation of turbulent flows[J].Comput Methods Appl Mech Eng,1974,80(3):269-289.
[12]COMINI G,GIUDICE S A.(k-ε )model of turbulent flow[J].Numer Heat transfer,1985,90(8):299-316.
[13]RAJAGOPALAN G,SCHALLER D,WADCOSK A J,et al.Experimental and computational simulation of a model ship in a wind tunnel[C]//43rd AIAA Aerospace Sciences Meeting.[S.l.],2005.

