海上超大型浮体的水弹性响应预报
万志男,翟钢军,程勇
(1.中交第四航务工程勘察设计院有限公司,广东广州510230;2.大连理工大学深海工程研究中心,辽宁 大连116024)
随着地球上人口的急剧膨胀,陆上资源供应已趋极限,为了缓解能源危机,各国都把经济发展的重点转移到海洋,海洋开发将形成如海洋油气工业、海洋化学工业、深海采矿业等一批新兴产业[1]。面对这一形势,国际海洋工程界掀起了研究超大型浮体(VLFS)的热潮,所谓超大型浮体是指那些尺度以公里计的浮式海洋结构物,其长宽方向与厚度方向的尺度比值较大,是一种极为扁平、柔度非常大的结构,必须考虑结构的弹性变形,这是一个典型的流固耦合问题,需要用由Bishop和Price[2]提出的水弹性理论分析,目前,日本、美国等国家取得了大量研究成果,以日本的超大型浮体(Mega-Float)和美国的移动海上基地(MOB)为代表[3-4],国内学者如吴有生[5-7]发展了适用广泛的三维水弹性理论,崔维成等[1,8]也对超大型浮体的结构动力特性及技术开发做了相关研究。滕斌等[9]比较了不同模态的收敛速度。黄国燕[10]提出了一种超大型浮体响应计算的简化方法。随着水弹性理论的不断发展,多种数值计算方法被应用于超大型浮体的水弹性计算中[11],特征函数法求解速度快,占用内存小,精确度高,本文采用特征函数法利用浮体结构的边界条件及板内外速度势及速度连续条件建立方程组求解速度势;应用模态函数展开法对板的挠曲变形进行模态展开计算结构的挠曲变形及弯矩分布,分别讨论了水深、波长及其他环境参数对超大型浮体水弹性响应的影响,并对水弹性问题中几种常用的模态函数进行了比较。
1 模型及基本假设
线性水弹性理论假定流体为均质、无粘、无旋、不可压缩的理想流体,把浮体假定为一个规则且与波浪的传播方向平行的薄板,图1是超大型浮体的薄板模型,x为波浪传播方向,z代表水深方向,板半长为b,板厚度为t,吃水量为d,水深为h。

图1 坐标示意图Fig.1 Sketch of coordinate system
基于上述假设,考虑线性近似下在等深度h水下传播的二维行进波问题,由于问题是线性的,速度势 Φ(x,z,t)和挠曲变形W(x,t)等物理量都是频率为ω的简谐函数。分离出时间因子e-iωt,得到速度势以及挠曲变形表达式如下:

式中:ω代表圆频率,w(x)为薄板的挠曲变形,选取一组适当的模态函数对其展开为

式中:N为模态数,ζl是对应第l阶模态的待求系数,fl(x)为对应薄板的第l阶模态函数。
2 速度势求解
根据流场特点,将流体沿±b划分为3个子域,对速度势进行特征展开,并在2个边界上对速度势和速度做连续匹配建立方程组求解速度势,这样计算量比较大,Mei和Black等[12]提出将上述问题分解成对称和反对称问题的处理方法,简化了计算量。流场中的速度势可分为3大部分:

式中:φⅠ为入射势,φD为绕射势,φlR为第l阶模态所对应的辐射势,入射势为
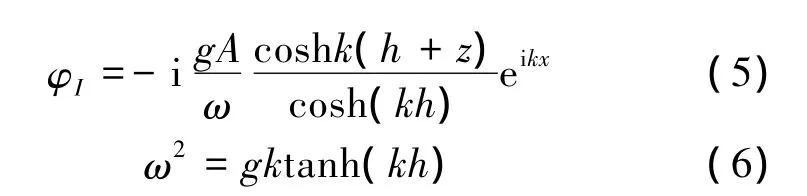
式中:g为重力加速度,A为波幅,k为波数。
2.1 流场控制方程和边界条件
假设流体为理想流体,波浪与浮体结构的相互作用问题可以归结为满足一定边界条件和初始条件的拉普拉斯方程求解问题。
流场的控制方程:

自由水面条件:
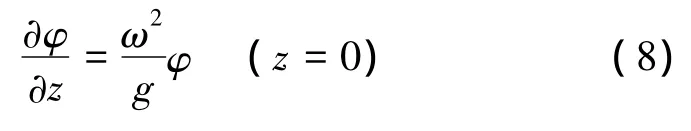
海底条件:

远场条件:
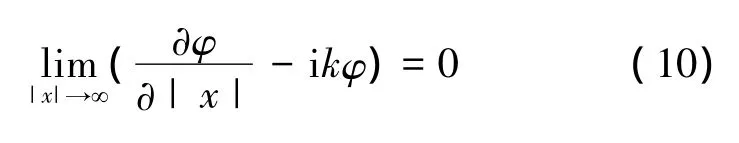
物面条件:
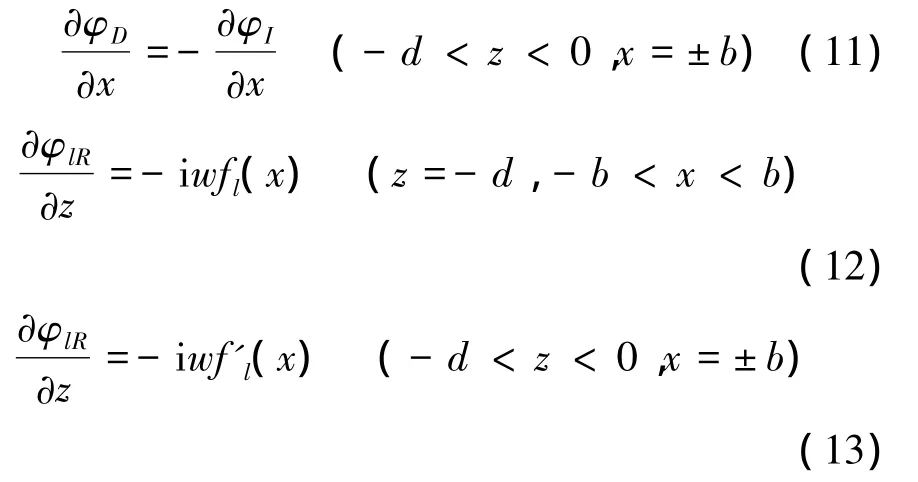
2.2 求解速度势
速度势可分解为对称和反对称速度势,对于辐射问题,入射波是不存在的,由于上下边界为非齐次边界条件,所以该区域的辐射速度势需要分解为通解和特解,速度势表达式为
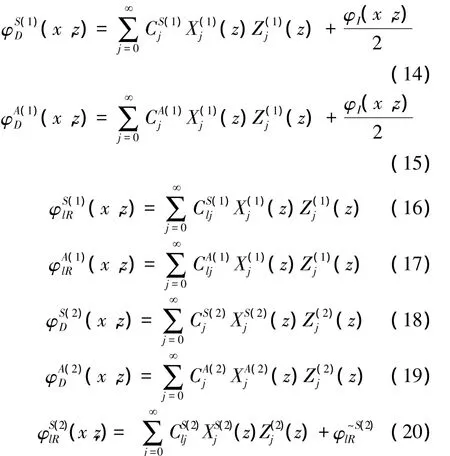

式中:上标S、A分别代表对称和反对称,为未知待求的绕射和辐射系数为辐射势特解,满足正交关系。

另外流体应该满足速度势和速度连续的匹配条件:

由速度势及速度连续条件求出绕射系数和辐射系数,得到各区域的绕射势和辐射势。
3 浮体结构运动方程
把超大型浮体简化为二维薄板,挠曲方程为
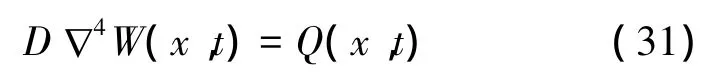
式中:弯曲刚度D=EⅠ,E为弹性模量,Ⅰ为截面惯性矩。
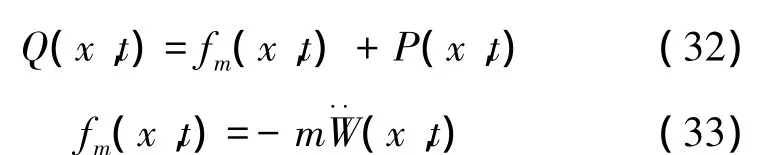
式中:fm(x,t)为惯性力,m为单位板长的质量,P(x,t)为薄板底部对应x处的流体压力。分离出时间因子后,弹性浮体的运动响应为
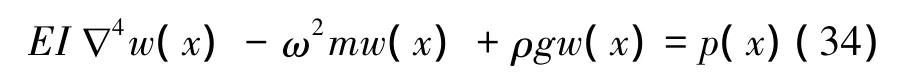
底板流体压力可以分为绕射引起的流体压力pD(x)和辐射引起的流体压力plR(x),其表达式分别为


式中:ρ为流体密度。把式(3)、(35)、(36)代入式(34)进一步得到弹性浮体的频域运动方程:
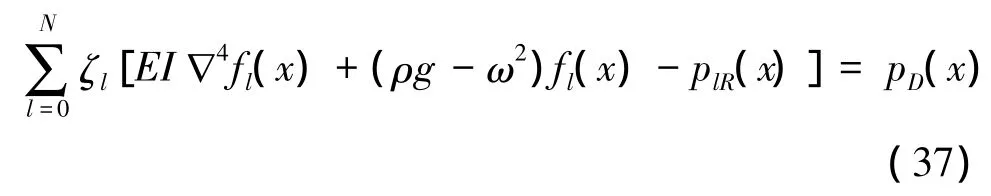
对上式两边同时乘以fi(x)并沿着薄板底面积分后得到弹性结构运动方程:
式中:Kij为刚度矩阵,Mij为结构质量矩阵,Maij为附加质量矩阵,Cij为辐射阻尼矩阵,Ci为流体作用力向量。浮体内部的弯矩可以求得

4 模态函数及特解
4.1 模态函数
水弹性问题中常采用 Newman[13]自然模态和Madea[14]自然模态,此外 Eatock Taylor 和 Ohkusu[15]利用刚体模态和正弦函数描述弹性梁的振动,余弦函数满足正交性,可作为模态函。滕斌,勾莹[9]对各种模态函数作了介绍,本文采用Newman自然模态。

式中:上标S、A代表对称模态和反对称模态,x的取值范围在-b~b,μSl和μAl满足特征方程:
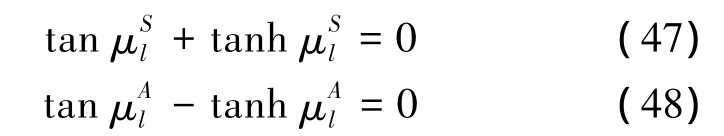
4.2 辐射势特解

5 数值结果分析
5.1 程序验证
为了验证数值方法及程序的可行性,以 C.Wu等[16]试验模型作为算例,比较计算结果与实验结果,试验模型的主要参数为:长10 m,宽0.5 m,高0.038 m,吃水0.008 36 m,弹性模量103 MPa,材料密度为220 kg/m3,图2为水深1.1 m,波浪周期为1.429 s薄板的水弹性响应位移和弯矩分布情况,本文计算结果与试验结果较好地吻合。


图2 波周期为1.429 s时薄板变形和弯矩分部Fig.2 Deflection and bending moment of floating structure at wave period 1.429 s
5.2 广义波浪激励力的计算
选用C.Wu等[16]的试验模型,计算不同水深下超大型浮体所受广义波浪激励力。如图3所示。


图3 水深0.8 、1.0 、1.2 m时的广义激励力Fig.3 Generalized wave exciting force at water depths of 0.8 、1.0 and 1.2 m
无量纲化后,取前8阶模态,发现能取得较好的收敛效果。
5.3 水深及波长对超大型浮体水弹性响应的影响
进一步研究在不同水深条件下,超大型浮体两端和中间的水弹性响应随波长的变化,结果如图4所示。
采用无量纲化,浮体中间的变形值随着波长增大而增大,而浮体迎浪端与背浪端变形值在个别区间内仍有波动,这点需要特别注意。取0.8 m、1.0 m和1.2 m 3个水深值,随着水深的增加,浮体两断以及中间处的变形并不是单调递增或者单调递减,在2b/λ<5时,浮体迎浪端与背浪端的变形值没有明显的变化规律,而中间处的变形值随着水深增加而减小,在2b/λ>5时,浮体的迎浪端、背浪端及中间处的变形值均随着水深增加而增大。
5.4 其他参数对浮体水弹性的影响
超大型浮体柔度较大,本文计算了水深为1.0 m,波长为4.0 m下浮体的变形随刚度的变化趋势。如图5所示,浮体的变形随着刚度的增加而减小。
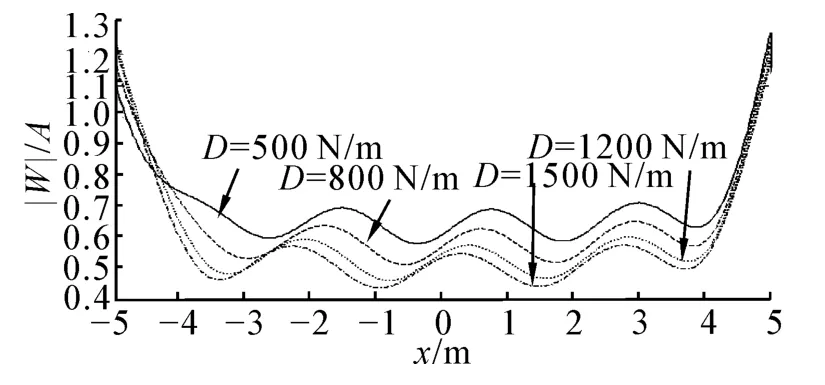
图5 不同刚度下浮体的变形Fig.5 Deflection of the structure at different rigidities
另外本文还探究了不同吃水深度下浮体的变形,下面给出了在水深为1.0 m,波长4.0 m下浮体变形值随浮体吃水深度的变化趋势,如图6所示,随着吃水深度不断增加,浮体的变形略微增大。

图6 不同吃水深度下结构的变形Fig.6 Deflection of structure at different draft
5.5 几种常用模态函数的比较
前面的研究都是建立在Newman模态上,类似地,还可以应用其他一些常用的模态函数来解决水弹性计算问题,对各种模态函数得到的计算结果与试验结果进行比较,如图7所示。

图7 不同模态函数的数值计算结果与实验结果的比较Fig.7 Comparison between experimental and computational results of different model functions
图7为Newman模态、Madea模态、正弦模态和余弦模态,周期分别为0.7 s和1.429 s时4种常用的模态函数的水弹性变形分布。
4 结束语
波浪于超大型浮体的作用是涉及结构动力学和水动力学的一门交叉学科,本文结合特征函数法和模态函数法,计算超大型浮体的水弹性响应,对比数值计算结果与国外学者的实验结果,发现两者较好地吻合。进一步分析了水深、波要素及其他环境参数对超大型浮体的水弹性响应的影响,同时对水弹性问题中几种常用的模态函数进行了比较,丰富了超大型浮体水弹性问题的研究,为超大型浮体的间接时域分析提供了参考依据。
[1]崔维成,吴有生.超大型海洋浮式结构物动力特性研究综述[J].船舶力学,2001,5(1):73-81.CUI Weicheng,WU Yousheng.Recent researches on dynamic performances of very large floating structures[J].Journal of Ship Mechanics,2001,5(1):73-81.
[2]BISHOP R.A general linear hydroelasticity theory of floating structures moving in a seaway[J].Philosophical Transactions of the Royal Society of London,Series A:Mathematical and Physical Sciences,1986,316:375-426.
[3]WATANABE E,WANG C,UTSUNOMIYA T,et al.Very large floating structures:applications,analysis and design[J].CORE Report,2004,2:104-109.
[4]TAY C W.Very large floating structures:applications,research and development[J].Procedia Engineering,2011,14:62-72.
[5]田超,吴有生.船舶水弹性力学理论的研究进展[J].中国造船,2008,12:1-11.TIAN Chao,WU Yousheng.Review of research on the hydroelasticity of ship[J].China Shipbuilding,2008,12:1-11.
[6]田超,吴有生.航行船舶的三维非线性水弹性分析[J].船舶力学,2007,11:68-78.TIAN Chao,WU Yousheng.Three-dimensional non-linear hydroelastic analysis on ships with forward speed[J].Journal of Ship Mechanics,2007,11:68-78
[7]WU Y,CUI W.Advances in the three-dimensional hydroelasticity of ships[J].Proceedings of the Institution of Mechanical Engineers,Part M:Journal of Engineering for the Maritime Environment,2009,223:331-348
[8]崔维成,吴有生.超大型海洋浮式结构物开发过程需要解决的关键技术问题[J].海洋工程,2000,18(3):1-8.CUI Weicheng,WU Yousheng.Technical problems in the development of very large floating structures[J].Ocean Engineering,2000,18(3):1-8.
[9]滕斌,勾莹.大型浮体水弹性作用的频域分析[J].工程力学,2006,23:36-48.TENG Bin,GOU Ying.Hydrostatic analysis of very large floating structure in frequency domain[J].Engineering Mechanics,2006,23:36-48.
[10]黄国燕,赵耀.超大型浮体水弹性响应的简化方法[C]//中国钢结构协会海洋钢结构分会2010年学术会议暨第六届理事会第三次会议论文集.洛阳,中国,2010.
[11]KOROBKIN A.The mathematical challenges and modelling of hydroelasticity[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,2011,369:2803-2812.
[12]MEI C C,BLACK J L.Scattering of surface waves by rectangular obstacles in waters of finite depth[J].Journal of Fluid Mechanics,1969,38:499-511.
[13]NEWMAN J.Wave effects on deformable bodies[J].Applied Ocean Research,1994,16:47-59.
[14]MAEDA H,MASUDA K,MIYAJIMA S,et al.Hydroelastic responses of pontoon type very large floating offshore structure[J].Journal-Society of Naval Architects of Japan,1995,178:203-212.
[15]TAYLOR R E,OHKUSU M.Green functions for hydroelastic analysis of vibrating free-free beams and plates[J].Applied Ocean Research,2000,22:295-314.
[16]WU C,WATANABE E,UTSUNOMIYA T.An eigenfunction expansion-matching method for analyzing the wave-induced responses of an elastic floating plate[J].Applied Ocean Research,1995,17:301-310.

