新型航标装置浮体水动力特性数值模拟研究
余 葵,戴一锋,孟繁超,毛德涵,刘 阳,梁家华
(1.重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;2.重庆交通大学 重庆市桥梁通航安全与防撞工程技术研究中心,重庆 400074;)
引言
山区河流航段的传统航标位于山高水急、坡度接近90 度的悬崖边,航标的维护需要在悬崖新型上开展高空作业,维护难度大,存在极大的安全隐患。为此,重庆交通大学研发了新型自浮升降式航标装置,解决了传统航标寿命短、易出故障及维护困难的问题,提高了行船的通航安全系数。
新型航标装置的水动力特性十分复杂,受大气环境、波浪条件、水流条件和材料性质等诸多因素影响。浮体结构的稳定性受到风、浪、流等因素的共同作用,装置运行时,浮体结构及部分导向柱长期在30 m 水位变动区工作,浮体结构受到波浪影响很大。因此,研究浮体结构在波浪情况下的运行稳定性(水动力特性)是十分必要的。
1 软件建模
国内外学者对海上船舶、海洋平台和海上风机平台等浮体结构的水动力特性进行了较多研究,Inglis 等[1-3]通过二维船舶运动理论和三维船舶运动理论分别求解了不同形状浮体的水动力响应数值结果。并基于非线性势理论,对三维浮体结构在不同入射角波浪作用下的相互作用进行了数值研究。王凌宇等[4-6]通过水动力计算软件AQWA 中的频域计算模块和时域模,建立了类海蟒式波能装置的仿真模型。在单向规则波作用下,利用频域模块分析了入射波频率的变化对浮体的垂荡、纵荡两方向上的运动响应幅值算子、附加质量、辐射阻尼的影响,利用时域模块分析了浮体所受波浪力、浮体位移和速度随时间的变化。以上研究成果为新型航标装置浮体受波浪作用水动力特性数值研究提供了理论研究基础。
1.1 模拟工况
本文主要研究新型航标浮体结构在波浪中的运动响应,试验要素主要有波高和周期。根据相关文献资料,三峡库区蓄水前最大风浪波高不超过1 m[7],结合现场调研,取重现期为3 年的波浪作为典型波浪,如表1 所示。
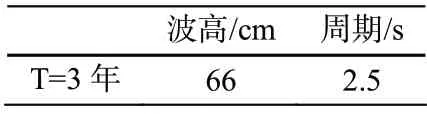
表1 波浪要素
试验选取浮体吃水深度为浮子高度的1/2 如表2 所示。

表2 模拟工况
1.2 模型建模
试验模型按1:15 比尺进行建模,因小尺寸浮体采用AQWA 软件所得计算结果不精确,浮体与导向柱之间的间距过小而不易实现滑动,故采用原型比尺进行建模计算。四种浮体高度均为2 m,其中环型、哑铃型、水滴型浮体长度为5.5 m,宽度为2.5 m,圆柱形浮体直径为2.2 m,建模如下图所示。

图1 浮体建模
1.3 网格划分
保证浮体最大允许频率大于试验波频0.4 Hz[8],因此,在浮体网格划分时,网格允许量和最大控制尺寸取为0.05 m 和0.25 m,自动划分浮体网格,如图2 所示。
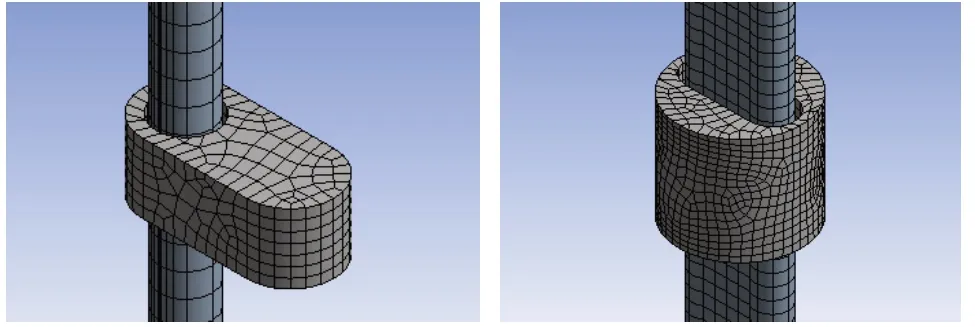
图2 网格划分
2 浮体水动力特性研究
采用AQWA 软件对浮体进行仿真计算,固定浮体的水平运动,在规则波作用下,分析浮体竖向运动响应幅值算子、附加质量和辐射阻尼及一阶波浪激振力随入射波频率的变化规律,探讨入射波方向和浮体形状对浮体结构水动力特性的影响。
2.1 运动响应幅值算子
在不同波频的波浪作用下,浮体结构在其平衡位置附近做往复振动,当入射波频率接近浮体结构的固有频率时,浮体结构就会发生共振。
单位规则波作用下浮体结构运动响应幅值算子(RAOs)[9](亦称传递函数)数学表达式为:

式中,R为浮体响应幅值,A为规则波波幅,H为运动响应幅值算子,其与入射规则波的方向以及浮体的位置和几何形状有关。在线性波理论的假设下,浮体的响应幅值与入射规则波的波幅成正比。
因本课题的水工物模试验是单向造波,为便于比较修正,也用AQWA 软件仿真模拟单向造波,每45°计算一次浮体的垂荡响应幅值算子。因浮体结构关于X轴对称,仅需分析与X轴夹角在0°~180°范围内的入射波向。在相同吃水及不同浪向角下不同形状浮体结构的垂荡响应幅值算子计算结果如图3 所示。
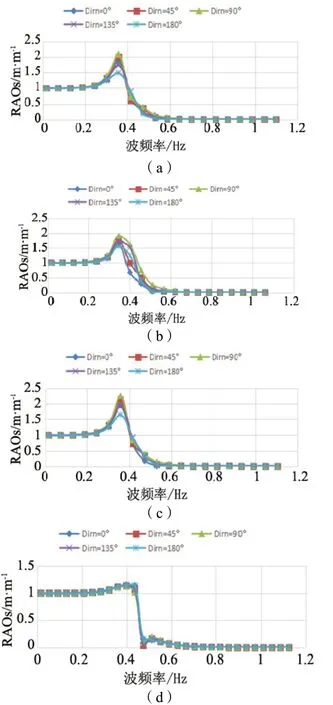
图3 4 种浮体不同浪向角的垂荡响应幅值算子
从图3 可知,环形、哑铃形、水滴形浮体均在0.36 Hz 左右出现峰值,其中90°浪向角时局部峰值最大,180°浪向角时峰值最小,说明三种形状浮体结构的垂荡RAOs 受浪向角的影响。而圆柱形浮体在各个浪向角下,垂荡RAOs 响应曲线几乎没变化,说明浪向角对圆柱形浮体的垂荡RAOs 几乎没影响。
浮体的运动响应幅值算子与浮体的结构存在直接关系,在180°浪向角下的不同形状浮体的垂荡RAOs 计算结果如图4 所示。

图4 不同浮体180°浪向角下垂荡响应幅值算子
由图4 可知,圆柱形浮体的垂荡RAOs 峰值最小,环形、哑铃形、水滴形浮体的垂荡RAOs 峰值较接近,水滴形的垂荡RAOs 峰值最大。说明圆柱形浮体受波浪的影响较小,而环形、哑铃形、水滴形浮体受波浪的影响较大。
由上述结论可知,圆柱形浮体的特征最典型,受波浪的影响最小。
2.2 附加质量与辐射阻尼
浮体的附加质量与辐射阻尼是浮体关于浮体形状、摇荡频率与前进速度的函数,当浮体在理想的流体中运动时,所受到的力与力矩可由速度、加速度以及附加质量与辐射阻尼决定,因此,对附加质量与辐射阻尼的研究非常重要[10]。
当浮体在理想的流体中运动时,四种形状的浮体垂荡方向上的附加质量系数和辐射阻尼系数计算结果如图5、6 所示。
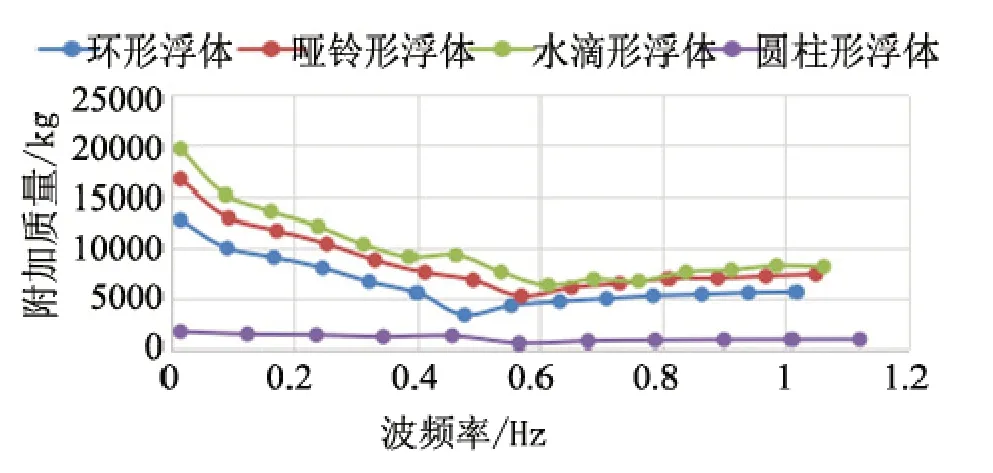
图5 浮体的垂荡附加质量系数
从图5 可知,浮体的垂荡附加质量系数大小与形状有关,其中圆柱形的垂荡附加质量系数最小,水滴形浮体的垂荡附加质量系数最大。
从图6 可知,与垂荡附加质量系数的趋势一致,浮体的垂荡辐射阻尼系数大小与形状有关,其中,圆柱形的垂荡辐射阻尼系数最小,水滴形浮体的垂荡辐射阻尼系数最大。

图6 浮体的垂荡辐射阻尼系数
2.3 一阶波浪力
在线性波理论的假定下,入射波浪在遭遇浮式结构时,会产生复杂的波浪绕射。一阶波浪力是考虑了绕射影响后的入射波浪对浮式结构的作用力,是Froude-Kriloff 力和一阶绕射力的叠加[10]。
浮体在不同浪向角的一阶波浪力计算结果如图7 所示:
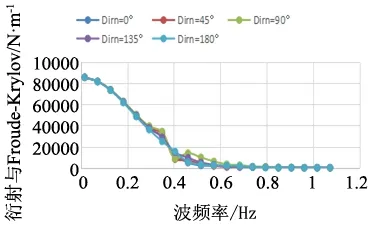
图7 相同浮体不同浪向角的垂荡一阶波浪力曲线
从图7 可知,浮体的垂荡一阶波浪力随浪向角变化不明显,说明浪向角对浮体的垂荡一阶波浪力影响较小。
分析不同形状浮体的一阶波浪力,在180°浪向角下浮体的垂荡一阶波浪力计算结果如图8 所示。

图8 浮体的垂荡一阶波浪力曲线
从图8 可知,浮体的垂荡一阶波浪力大小与形状有关,其中,圆柱形浮体的垂荡一阶波浪力最小,水滴形浮体的垂荡一阶波浪力最大。
3 结语
通过AQWA 软件分析装置中浮体的水动力特性。本文的结论如下:
1)三种形状浮体结构的垂荡RAOs 受浪向角的影响,而圆柱形浮体结构受浪向角的影响最小。
2)浮体结构的垂荡附加质量系数大小与形状有关,其中圆柱形的垂荡附加质量系数最小,水滴形浮体的垂荡附加质量系数最大。
3)浮体结构的垂荡一阶波浪力大小与形状有关,圆柱形浮体的垂荡一阶波浪力最小,水滴形浮体的垂荡一阶波浪力最大。
根据数值模拟得出圆柱形浮体水动力特性最优,验证了圆柱形浮体的稳定性。
——蝴蝶

