高精度模糊控制器在水轮机调节中的应用

曹 欢， 杨 棣

(中国长江电力股份有限公司三峡水力发电厂，湖北 宜昌 443000)

0 引 言

水轮机调节系统是一个高度非线性的、时变的复杂控制系统，系统内含有时滞、转速死区，而且还呈现出非最小相位特性。尽管现在的微机调节器多种多样，但就其调节规律而言，多为传统的PID，真正的高级控制策略目前还在研究和试验阶段。之前很多学者将模糊控制理论用于水轮机调节控制中[3-4]，其调节规律有着明显的改善，减小了系统的超调量，增加了系统的稳定性。模糊控制是一种专家系统，他需要工作人员在长期工作中积累的经验，并实现了数学表达。然而，在利用模糊控制理论的时候，其论域很难确定，往往要花很长时间对其调试，才能达到较好的论域值，且该论域值在试验中不能进行调整，无法实现自适应的要求，针对此问题，我们设计了一类基于变论域的高精度模糊控制器[5-6]，它是在模糊PID控制基础上对原有的模糊控制进行了改进与优化，使模糊控制器在微偏差范围内也能保证精度的要求，且不改变其粗调快速的优点。

1 控制器设计

1.1 PID控制器

PID器也称为比例-积分-微分控制器，已有70多年的应用历史，作为最早实用化的工业控制器到现在依然有着最广泛的应用。PID控制器算法简单，对于连续PID算法有：

(1)

(2)

(3)

公式(2)减去(3)，经过化简可得增量式数字PID算式：

△Dy(n)=Dy(n)-Dy(n-1)=Kp[e(n)-e(n-1)]+Kie(n)+Kd[e(n)-2e(n-1)+e(n-2)]

(4)

1.2 模糊PID控制器

模糊集合理论(Fuzzy Sets)[5]是美国加州大学Zadeh L A教授于1965年提出来的，其实质就是在描述复杂系统时，当有效性和精确性无法兼顾时可以进行模糊处理。

设X是对象x集合，x是X上任意一个元素。X上的模糊集合A定义为一组有序对。

A={(x,μ(x))|x∈X}

(5)

其中μ(x)称为模糊集合A的隶属函数(Member Function，MF)，X称为论域。模糊集合完全由隶属函数所表征。模糊PID控制最重要的步骤是找出比例(Proportion)、积分(Integration)和微分(Differentiation)系数与误差e、误差对时间的一阶导数ec之间的关系，关系的建立主要基于以下几个原则[8]：

(1)当|e|较大时，为使系统具有较好的跟踪性能，Kp应取较大，Kd应取较小。同时为了避免出现较大的超调，应对积分作用加以限制，Ki通常取0；

(2)当|e|处于中等大小时，我们希望系统响应具有较小的超调，Kp应取得尽量小，此时，Kd的大小对系统响应的影响就比较大，Ki的取值要适当。

(3)当|e|较小时，为使系统具有较好的稳定性能，Kp和Ki的值都应取的大些，同时为避免系统出现振荡，Kd值的选择根据ec来确定；当ec值较小时Kd取大些，当ec值较大时Kd取小些，Kd值通常是中等大小。

然后根据规则列出模糊规则表，实现在线自适应调整。

1.3 高精度模糊PID控制器

高精度模糊控制器采用变论域(Variable Universe)思想，思想的实质是根据实时变化的实际情况对原先不能改变的初始论域进行在线自适应的论域伸缩。

图1 论域压缩

常用的模糊控制规则模型如Mamdani模型等，从数值分析的角度理解，皆为一种插值函数。两峰点之间的距离就决定了精度的高低。传统的模糊控制不能改变峰点之间的间距，精度基本不变，不能使模糊规则更好地发挥控制作用。因此，我们引进伸缩因子α(x)和β(x)[1-2]，不妨假设输入变量的初始论域Xi=[-Ei，Ei](i=1，2，…)，添加伸缩因子之后变成Xi=[-α(x)Ei，α(x)Ei]，其中α(x)是输入变量x的连续函数，且满足：

α(x)=1-λe-kx2λ∈(0,1)k>0

(6)

同理β(x)作用于输出变量论域中，且满足要求：

(7)

变论域的关键就在于确定伸缩因子的大小，使得最终的控制效果达到最优。

2 水轮机调节器数学模型

水轮机调节器的数学模型我们都以传递函数的形式来表示，对于线性定常系统的的传递函数，是分别通过Laplace变化的输出量与输入量的比值，以s为变量的代数方程。

电液随动系统的数学模型为：

(8)

式中Ty是主接力器时间常数；Ty1是引导阀和辅助接力器时间常数。当Ty1与Ty相比小得多时，上式近似表示为：

(9)

水轮机组段数学模型(以y→mt为例)：

(10)

式中ey是水轮机力矩对导叶开度的传递系数；eqy是水轮机流量对导叶开度的传递系数；eqh是水轮机流量对水头的传递系数；Gh(s)是有压过水系统传递函数，假设为刚性水击，即认为管壁和水流都不可压缩，Gh(s)= -Tωs，Tω是水流惯性时间常数。

上式可简化为：

(11)

水轮机力矩到发电机转速的数学模型：

(12)

式中Ta是机组惯性时间常数；eg发电机(负荷)自调节系数；ex水轮机自调节系数。

3 高精度模糊控制器仿真

该水轮机调节器模型图由图2所示：

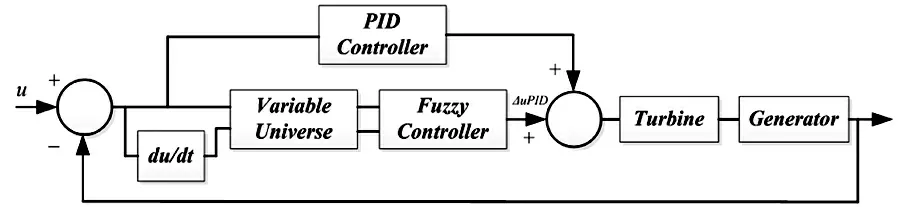
图2 高精度模糊控制器模型

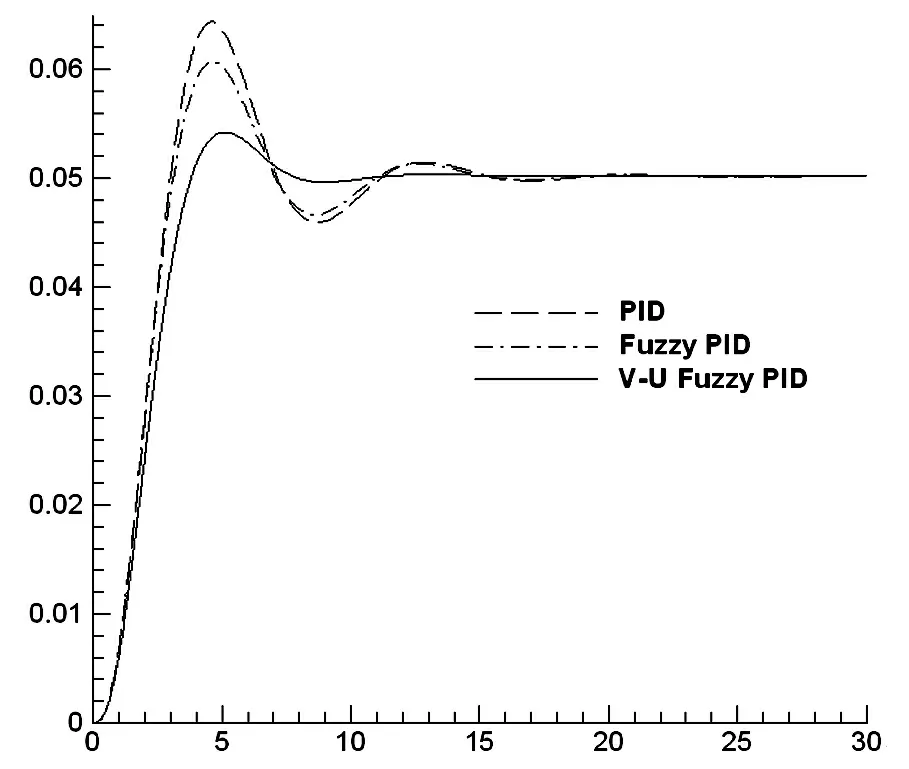
图3 发电机频率变化5%时阶跃响应

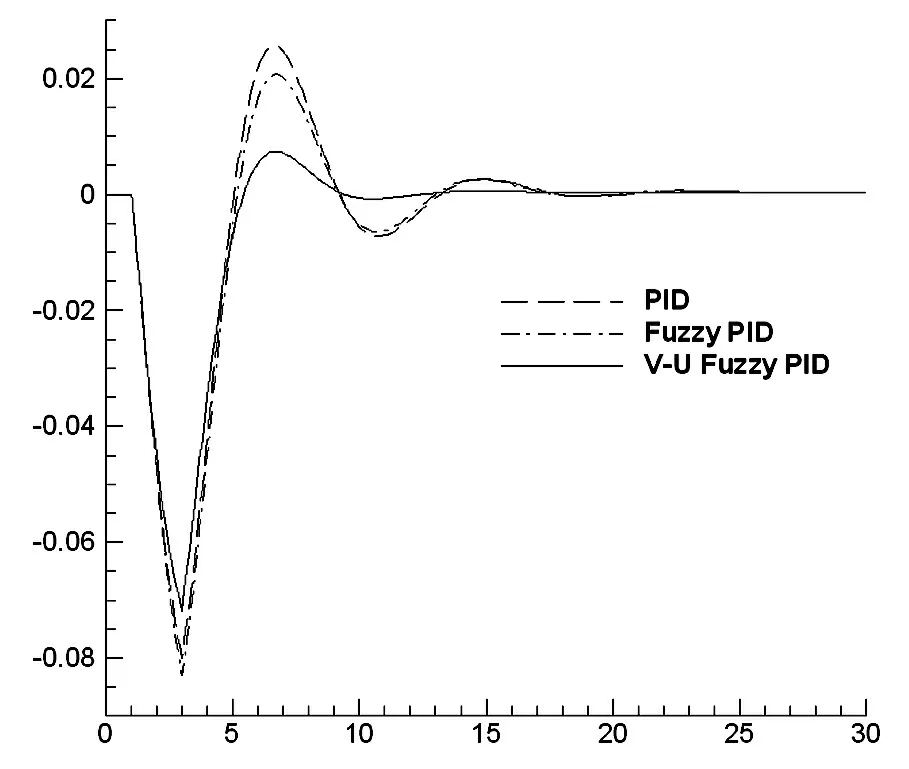
图4 甩10%负荷时的发电机转速阶跃响应

其调节对象的各项参数为：ey= 0.57，eqy=0.69，eqh=0.51，Tω=1.45 s，Ta=5.66 s，eg-ex=1。以下我们分别对比传统PID控制器、模糊PID

控制器和高精度模糊控制器分别在两种工况下的状态响应。

(1)无负载扰动的情况下，增加2.5Hz的频率扰动。

(2)无频率扰动的情况下，加入10%的负载扰动，见图4。

4 结 论

通过传统PID控制器、模糊PID控制器和高精度模糊PID控制器在频率扰动和负荷扰动两种工况下的扰动可以清晰的看到，高精度模糊控制器相比于另外两种控制器，动态特性好，曲线过冲小，较强的抗扰动能力；调节能力强，速度快且过程平稳；鲁棒性强，综合性能较优。是一种行之有效的控制方法，该高精度模糊控制器在工业系统控制中将有广阔的应用前景。

参考文献：

[1] 李洪兴. 变论域自适应模糊控制器[J].中国科学(E辑)，1999，29(1)：32-42.

[2] 李洪兴.非线性系统的变论域稳定自适应模糊控制器[J].中国科学(E辑)，2004，32(2)：211-223.

[3] 陈国平，孙培德，李俐，等.模糊控制器在水轮机调节中的应用及Simulink仿真[J].水力发电，2006，32(7)：53-55.

[4] 喻菁，周建中.模糊PID控制在水轮机调节中的应用研究[J].水利科技，2003，1：49-54.

[5] 李洪兴. Fuzzy控制的本质与一类高精度Fuzzy控制器的设计[J].控制理论与应用，1997，14(6)：868-872.

[6] 田勇，沈祖诒.水轮机调解中高精度模糊控制器的应用[J].水利水电科技进展，2006，26(5)：55-58.

[7] Zadeh L A. Fuzzy Sets[J]. Information and Control，1965，8：338-353.

[8] 李勇. 水轮机调节系统模糊PID控制器设计及仿真研究[J].工程技术，2010，75-79.

作者简介:

曹 欢(1984-)，男，湖北钟祥人，工程师，电气工程及其自动化本科毕业，从事水电厂运行维护工作；杨 棣(1990-)，男，山东无棣人，助理工程师，热能与动力工程本科毕业，从事水电厂运行维护工作.