谈谈动态平衡中那些不变的力
(南京市第二十九中学,江苏 南京 210036)
共点力平衡问题是高考的热点,尤其是动态平衡问题.所谓“动态”即有力在变,所谓“平衡”即在变化的整个过程中物体受到的所有力的合力为零,这样的状态我们也称为准静态.也就是无限接近静止状态,其实可以当成静止来处理.动态平衡问题通常会出现“缓慢”、“慢慢”、“逐渐”等典型的表述,抓住这些字眼然后结合题意进一步分析.我们发现在共点力动态平衡问题中,有这么一类题,条件在发生变化,物体也在缓慢移动.从表面看在动,其实各力的大小和方向都保持不变.这样的题有什么样的特征,用到哪些知识,应该如何分析,就让我们一起来探讨吧.
1 问题的由来
通过下面的例题,我们希望找到这类题所遵循的共同规律,达到做一题会一类的效果.
例1 如图1所示,晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,绳子的质量及绳与衣架挂钩间摩擦均忽略不计,衣服处于静止状态.如果保持绳子A端在杆上位置不变且绳长也不变,将B端在杆上分别移动到不同的位置.下列判断正确的是( ).

图1
A.B端移到B1位置时,绳子张力不变
B.B端移到B2位置时,绳子张力变小
C.绳对挂钩的弹力变小
D.绳对挂钩的弹力不变

图2
分析:对挂钩进行受力分析,如图2所示,受竖直向下的拉力FT(大小等于衣服的重力G)、沿绳的拉力FT1和FT2.由于是光滑的挂钩挂在绳子上,而同一根绳子上的拉力相等,即FT1=FT2.又因为衣服处于静止状态,FT1和FT2的合力与FT等大反向.所以FT1和FT2的合力方向竖直向上,那么绳OA和OB与竖直方向的夹角相等都为θ.且有2FT1cosθ=mg.
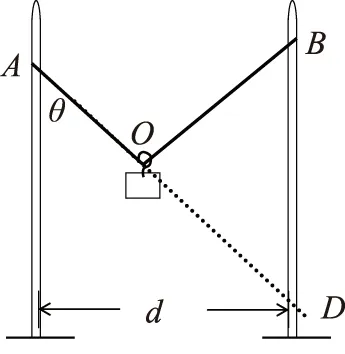
图3
设绳子的长度为L,两杆间的距离为d,那么延长AO交另一杆于D点,如图3所示,由几何关系易得OB等于OD,那么AD就等于绳长L.所以sinθ=d/L.那么在保证A点不动的情况下将B点移动到B1或B2,绳长不发生变化,即θ不变,所以绳中拉力不变.移动后的图形如图4所示.答案为A、D.
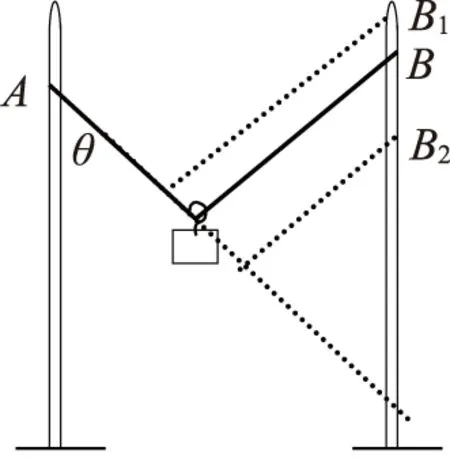
图4
通过上面的分析我们发现,无论B点在杆上怎么移动,只要保证L和d不变,那么θ角就不变,两力的夹角不变,两力的合力也不变,那么这两个力必然不变.
2 问题的探究
当然,我们不必满足于B点在杆上移动的情况,其实掌握上面的规律,B点无论移动到哪里我们都可以很快的给出答案,不妨来看下面例题.
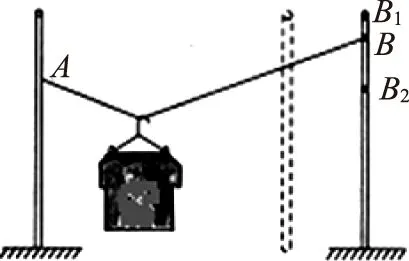
图5
例2 如图5所示,晾晒衣服的绳子轻且光滑,悬挂衣服的衣架的挂钩也是光滑的,轻绳两端分别固定在两根竖直杆上的A、B两点,衣服处于静止状态.如果保持绳子A端位置不变,将B端分别移动到不同的位置.下列判断正确的是( ).
A.B端移到B1位置时,绳子张力变大
B.B端移到B2位置时,绳子张力变小
C.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变大
D.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变小
分析:在上题的基础上,在杆上移动B点不改变θ角,很快判断A和B都是错的.将杆移动到图中虚线位置,那么d变小,而L不变,则根据sinθ=d/L得θ角变小.再根据力的合成规律,两个大小相等的力保持合力不变,减小两个力的夹角,那么这两个力都变小.可以判断D正确.
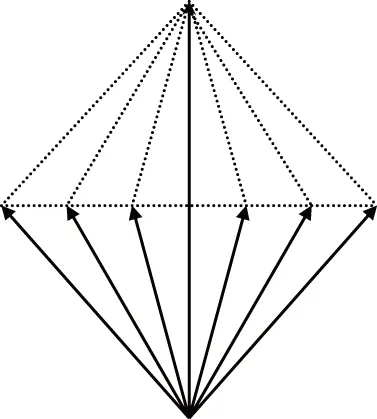
图6
这让我们想到两个小孩提一桶水,怎样提最省力.无论两小孩手臂之间的夹角多大,水的总重力是一定的,即两个小孩对水的拉力的合力是个定值,所以在夹角变小时拉力变小.可以从图示中直观的得出这个结论,如图6所示,在对角线不变的情况下,两临边夹角越小,这两个边越小,即分力越小.
例3 在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图7所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高).则绳中拉力大小变化的情况是( ).
A.先变小后变大
B.先变小后不变
C.先变大后不变
D.先变大后变小
分析:当绳子的右端从B点移动到支架右侧圆心等高处的过程中,绳子和竖直方向的夹角θ在不断变大,所以绳中的拉力也随之增大.再往下移到C点的过程中,θ角不变,所以绳中拉力不发生变化.所以绳中拉力大小变化的情况是先变大后不变.故选C.
掌握了这其中的规律,知道绳子端点的移动导致的绳子和竖直方向的夹角变化情况,竖直移动夹角不变,水平靠近夹角变小,水平远离夹角变大.再根据力的合成的知识,在合力不变的情况下,两等大的分力的大小随夹角的变大而变大、变小而变小.这样一来,做这类题就觉得很轻松了.
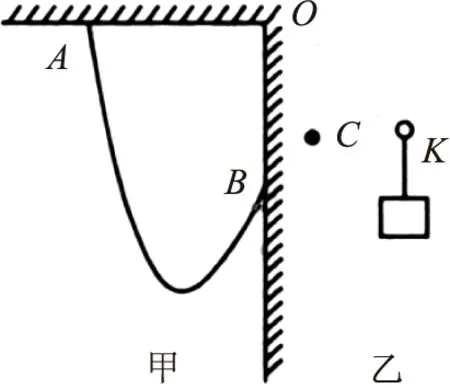
图8
例4 如图8甲所示,将一条轻而柔软的细绳一端拴在天花板上的A点,另一端拴在竖直墙上的B点,A和B到O点的距离相等,绳的长度是OA的两倍.图8乙所示为一质量可忽略的动滑轮K,动滑轮下端悬挂一质量为m的重物.一切摩擦可忽略.
(1)现将动滑轮和重物一起挂到细绳上,在达到平衡时,绳所受的拉力是多大?
(2)保持A点固定不动,将B点逐渐上移至O点,绳子的拉力如何变化?
(3)保持A点固定不动,将B点逐渐上移至C点,绳子的拉力如何变化?
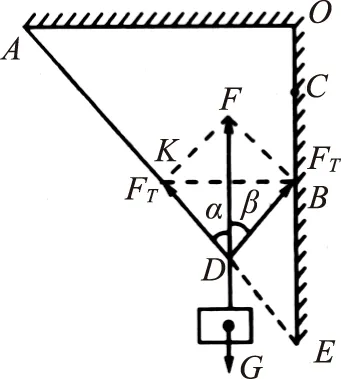
图9
分析:(1)画出动滑轮和物体达到平衡时的受力图(如图9).由于滑轮是挂到绳上的,AB仍为一条绳,因此绳各处的张力大小相等.

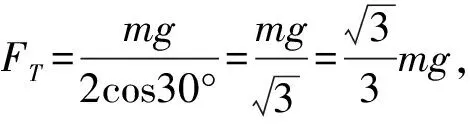
(2)保持A点固定不动,将B点逐渐上移至O点,两绳与竖直方向的夹角不变,所以绳子拉力不变.
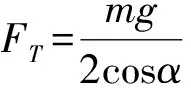
3 问题的一般意义
要能够真正掌握这类题的规律,还得学会去分析问题最本质的东西.不能肤浅的认为水平移动θ角就变化.最本质的是力的合成的知识和共点力平衡的条件.
例5 如图10所示,A、B两物体的质量分别为mA、mB,且mA>mB,整个系统处于静止状态.滑轮的质量和一切摩擦均不计,如果绳一端由Q点缓慢地向左移到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角θ的变化情况是( ).
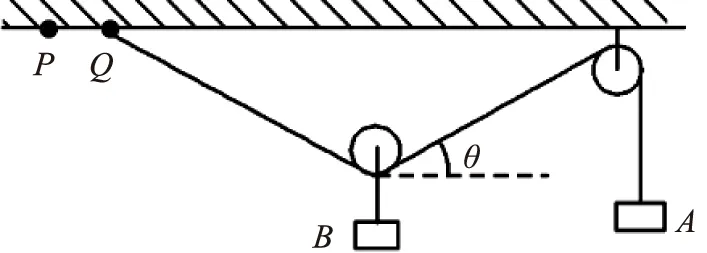
图10
A.物体A的高度升高
B.物体A的高度降低
C.θ角不变
D.θ角变小
分析:由于Q点在缓慢移动,所以系统始终处于平衡状态.对A分析可知,绳中的拉力FT大小始终为mAg.对B分析,由力的平衡可得2Fsinθ=mBg,故θ角不变.又因悬点由Q移动到P,左侧部分绳子变长,如图11所示,故A应升高.所以A、C正确.
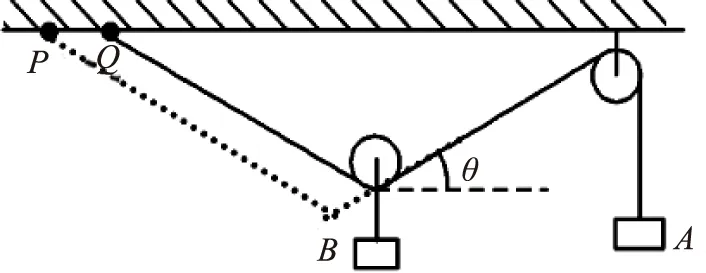
图11
这道题看上去悬点在水平移动,但和前面的题是不同的.通过对A的分析可知绳中的拉力始终不变,这样就可以从力不变推知夹角不变,和前面的由夹角不变推知力不变刚好相反.题目是千变万化的,但所考察的知识和规律是相对固定的,只有掌握了其中的解题方法才能以不变应万变.
参考文献:
蒋亚林 .力学动态平衡问题解法指导 . 中学物理, 2014,32(1) .
吴含章 .力学动态平衡问题的解法类析 .新高考:高一物理,2013,(5) .

