论动量定理教学的逻辑与结构
(1.首都师范大学物理系,北京 100048;2.北京市通州区玉桥中学,北京 101101)
1 传统教学的问题与分析
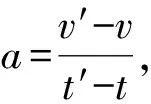
事实上,在1994年就曾经有教师对动量定理应用的相关问题进行过调查和统计.这位教师参加当年高考阅卷工作后发现,填空题中得分率最低的是一道涉及动量定理的题目,于是对420名考生的试卷进行了统计,其中有12.1%的学生写了正确答案,有47.1%的学生仅仅因为运用动量定理的过程中没有考虑重力的作用而写了错误答案,剩下的则可能是由于各方面原因没有写出正确答案.以上结果表明,在日常教学中处理打击碰撞等问题时,过分强调和突出冲力的作用,因而重力往往被学生忽略掉.
我们认为,前人的研究是非常重要的,这些研究结果应当得到肯定并给予重视,然而在现行人教版教材的例题解析中,运用动量定理时仍然没有任何有关重力的讨论,而直接忽略重力的存在,极易给学生以“碰撞问题中重力一定可以忽略不计”的错误认识.
此外,我们认为教材中动量定理推导过程的引入与学生的认知不相符合,动量定理与学生之前接触到的物理知识最大的不同是时间参量的介入,从时间参量的影响效果出发更容易给学生造成认知上的冲突.而且,教材中提到动量定理不仅适用于恒力情形,也适用于变力情形,但是对于为什么适用于变力情形并没有给出具体证明,不能有理有据地给学生呈现定理的来龙去脉,致使学生对定理的应用范围没有清晰透彻的理解.
2 教学的设计与阐释
基于以上认识,我们对“动量定理”一节进行深入研究,提出了以下教学设计,教学逻辑图如图1所示.

图1
(1)生活化的定理导入
教师在上课之前给学生布置课前作业,让学生回家学习煮鸡蛋,用煮熟的鸡蛋完成课外探究实验“能让熟鸡蛋落地而不破壳吗?如果可以,最高能从多高的地方落下而保证鸡蛋不破?”
课堂开始,教师先请几个小组选出的代表分别将本小组的最好成果演示给大家,实验结束后实验材料放置在讲台留作观察之用.接下来,教师提出问题:“为什么生活中常见鸡蛋落地会摔破,在今天的课堂中能够有所改变,有的同学能将鸡蛋从那么高的地方落下而鸡蛋完好无损?”同学们可以分析出应该是跟“地面”的硬度有关,在教师的引导下学生进一步推测“鸡蛋落地的高度与‘地面’的碰撞时间有关,鸡蛋初始位置越高,碰撞时间越长.”然后,教师再提出问题:“鸡蛋与‘地面’碰撞的过程中有哪些物理量发生了变化?”大部分同学可以分析出鸡蛋的速度从一个较大值变成了零.有些善于思考的同学则会想到新学的动量P也发生了变化.对此,教师给予适时引导使学生明晰“鸡蛋初始位置越高,碰撞过程中动量的变化量就越大”.于是,教师可以顺理成章地引出本节课的主题:既然鸡蛋初始位置越高,则碰撞时间越长、动量的变化量就越大;鸡蛋的动量变化量和碰撞时间之间是否存在一定的关系呢?下面我们来研究这个问题.
(2)彰显科学方法的定理推导
显然,鸡蛋与地面碰撞过程中,鸡蛋所受到的合力一直是变力,如果直接讨论全过程,运用现阶段物理知识分析起来会比较困难.因此我们可以运用数学上的极限法,把碰撞过程“无限细分”为n个时间段,n趋近于无穷大.这样每一个极短的时间段内,物体所受到的合力可以近似看作是恒力,即运动过程可以看作是匀变速直线运动.
我们设鸡蛋的质量为m,刚与地面接触时的速度为v0,动量为P0;第一个极短的时间段时间为Δt1,所受合力为F1,加速度为a1,末时刻速度为v1,动量为P1,动量变化量为ΔP1;第二个极短的时间段时间为Δt2,合力为F2,加速度为a2,末时刻速度为v2,动量为P2,动量变化量为ΔP2;以此类推,设最后一个极短的时间段时间为Δtn,合力为Fn,加速度为an,末时刻速度为vn,动量为Pn,动量变化量为ΔPn.
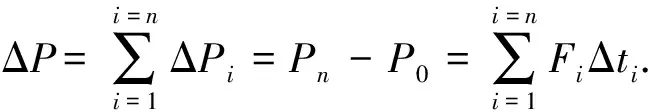
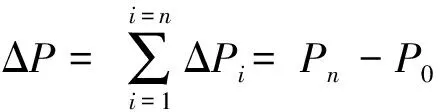
(3)在变式中体现定理应用
依据由简到繁、由抽象习题到原始问题的思路,我们设计了如下包括物理变式起点、节点、落脚点的三个问题,其变式教学结构如图2所示,并结合以下例题进行教学.
例1 一冰球m=50g,以15m/s的速度滚来,运动员用球杆将球击回,速度变为45m/s,打击时间为0.01s,求撞击力.
此典型例题的解答能够较好地诠释动量定理的重要特征和物理意义,求解时需要学生注意以下问题:(1)动量定量是矢量式.(2)动量定理不仅适用于恒力,同时也适用于变力,从而拓宽了解题口径.(3)碰撞问题中重力能否忽略不计需要看情况而定,只有碰撞时间极短,重力与碰撞力相比极小的情况下才能忽略不计.
例2 质量m=10kg的物体,放在光滑水
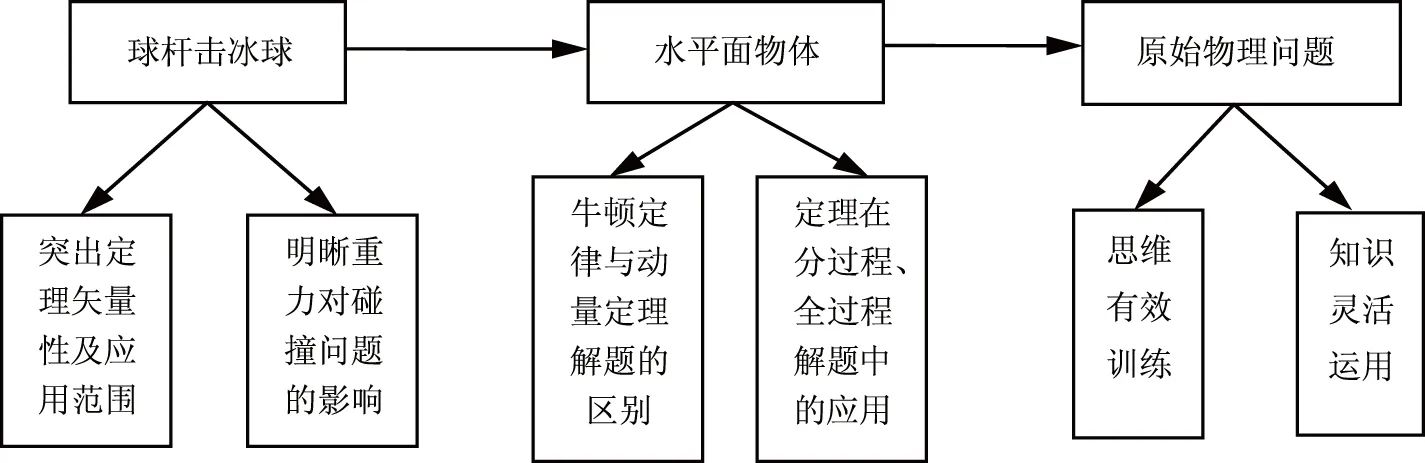
图2
平面上,现施F=100N的水平推力,求该物体在2秒时的速度?
拓展一:假设水平面不光滑,有摩擦力f=40N,其他条件不变,求物体2秒时的速度.
拓展二:在拓展一中,如果在2秒时撤去外力F,物体还能运动多久(设摩擦力不变)?
本例题经由两次拓展,充分展现了动量定理与牛顿定律的区别和联系,在不同情形下的定理应用,可达到训练学生知识迁移能力之效果.原题目采用一题多解,解法一,用牛顿定律和运动学公式求解;解法二,用动量定理求解,由此学生可以更深刻的认识牛顿定律和动量定理的联系.拓展一着重强调动量定理应用时是合力的冲量,应作好受力分析.拓展二亦可一题多解,解法一,分过程用动量定理;解法二,全过程用动量定理.三个问题步步深入,突出应用动量定理解题的好处:不涉及运动过程中的加速度和位移,用它处理问题比用牛顿定律方便;全过程用动量定理要比分过程用动量定理更加方便;应用动量定理时要注意是合力的冲量.
例3 在一起发生在很短时间的撞车中,需要多大的力才能抱住怀中婴儿,保证婴儿的安全?
这一原始物理问题由于没有提供具体的数据,所以需要由问题的特点提取出原始问题的本质,即问题是什么.在认识问题之后,要搞清楚问题的科学背景和相关知识,对问题中事物的本质属性进行分析、综合、比较,抽取出事物的本质属性,据此设置相应的参量,原始问题便被抽象为对应的习题.然后应用相关物理知识,推导得出结论.由于原始问题具有开放性,不一定具有唯一答案,所以对结论要持怀疑态度,并对结论进行评价.
该变式组的完成可以采取教师精讲与学生练习相结合的方式,教师只需引导学生解决1、2两题,在解题过程中让学生更深刻地体会动量定理的物理意义和适用条件.最后,问题的情境性从抽象到生态化过渡,利用原始物理问题的介入不仅使学生的逻辑思维得到训练,同时非逻辑思维也能得以提升.
3 教学的总结与启示
(1)实现物理新授课导入的生活化
传统教材利用运动钢球碰到墙壁后弹回的例题引出推导过程,脱离学生的生活经验,而且将整个物理现象“掐头去尾留中段”,很难激起学生的学习兴趣.比较而言,我们的教学设计由学生的演示实验导入,实验内容是我们日常生活中经常会遇到的现象:鸡蛋落地.演示实验中鸡蛋从高空落下完好无损的现象,与学生“鸡蛋落地很容易摔破”的生活经验产生了冲突,这一认知冲突是教学得以“破题”并顺利展开的关键.由此可见新授课导入生活化的重要作用与价值,我们认为,这一做法值得被物理教学广泛采用.
(2)在理论推导中实现物理思维的训练
物理学的基本特点要求教学应当重视理论推导,这种理论推导需要学生具有较强的物理思维能力和运算能力.教学中,通过呈现鸡蛋落地不破的实验现象,学生在教师的引导下分析出动量变化与碰撞时间可能存在一定联系,由此作为切入口,利用极限法、近似法、求和法进行演绎推理,进而得出动量定理的表达式.这样经由理论推导,整个过程脉络清晰、环环相扣,体现了推导的规范性、以及可操作性、可把握性,从而使学生深刻地体验到科学方法的效用和魅力,并自然地训练学生的逻辑思维.
(3)重视物理变式教学的设计与研究
动量定理蕴含的物理意义需要学生全面透彻地理解和运用,新授课中的练习就显得尤为重要.本节中,首先,动量定理的物理意义决定了其矢量性的特点,对此学生要非常明确,而且碰撞问题中重力能否忽略学生需要具备自己的判断,就该问题通过教师在新授课中对典型例题的解析可以加深学生的认识.其次,通过一题多问、一题多解的题目设置,使学生认识到动量定理与牛顿第二定律的区别和联系,以及定理在不同情况下的运用方法,从而达到明晰定理内涵、完成知识迁移之目的.最后,通过原始物理问题的设置,可以让学生的直觉思维、抽象思维等思维能力得到发展,从而提高解决实际问题的能力,实现物理变式教学生态化的落脚点.由此,正如有论者所言:通过变式教学由易到难、由近及远、由抽象到生态化的系统平台,学生思维方法的训练可以有序展开和逐步提升,并能成为突破物理思维障碍的“利器”.
参考文献:
人民教育出版社,课程教材研究所,物理课程教材研究开发中心.物理(选修3—5).北京:人民教育出版社,2010:7-9.
陶昌宏.从一道高考题谈动量定理的教学.物理教师,1994,(12).
向之乎.《动量定理》创新教学设计.物理教学探讨,2006,(12上).
蔡燃,陈清梅,邢红军.原始问题教学--培养创造性思维的新途径.教育理论与实践,2008,(5).
胡扬洋,陈清梅,邢红军.中国物理变式教学研究:传统与发展.教育导刊,2014,(2上).

