浅海中单矢量水听器高分辨方位估计方法
李楠松,朴胜春,宋海岩,张海刚
(1.哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;2.黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨150050)
与传统的声压标量水听器不同,矢量水听器可以同时、共点地测量声场中该处的声压和3个方向上的振速,即依靠单个矢量水听器就可以完成水下目标的方位估计,因而它的应用受到越来越大的重视,因此基于单矢量水听器的方位估计问题是水声信号处理研究的一个重要领域[1-3]。近年来,国内外关于单矢量水听器方位估计问题取得了一些研究成果,如文献[4]给出了4种基于声强流谱的单矢量水听器方位估计方法;Nehoria在文献[5]中提出了基于声强流矢量分解和基于速度协方差分解的2种方位估计算法等。
目前绝大多数单矢量水听器的方位估计都是基于声能流的最大似然估计[6],而高分辨方位估计算法是建立在基于空间分布阵列模型的基础之上,而且针对宽带信号的处理还要建立起相应的频域模型。根据单矢量水听器本身就具有阵列流型且不需要传统阵列处理中需要对阵列进行校准这一特点,将阵列信号处理中常用的高分辨算法应用于单矢量水听器,使其拥有以往只有阵列信号处理才能得到的高分辨方位估计能力[7-8]。然而,在远程方位估计问题中,不可避免需要考虑信道对方位估计的影响。在不能与实际声传播条件精确匹配的情况下,高分辨方位估计方法的估计精度及稳健性将会下降。鉴于此,本文充分考虑浅海信道对声传播的影响机制,首先推导出简正波理论下单矢量水听器的信号接收模型,然后将其与矢量最优化理论相结合,同时针对环境失配和系统失配问题,设置合适的最优化目标函数,获取该优化问题下的最优权矢量,得到简正波模型下的稳健处理器形式,以提高对失配问题的适应性和稳健性。
1 单矢量水听器的简正波接收模型
在理想情况下,N个远场窄带信号入射到空间L元阵列上,阵列接收窄带信号的波达方向(DOA)数学模型为
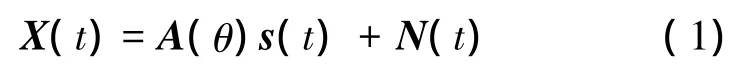
式中:A(θ)是空间阵列的L×N维流型矩阵,X(t)是阵列的L×1维快拍数据矢量,s(t)是空间信号的N×1维矢量,N(t)是阵列的L×1维噪声数据矢量。不考虑海洋信道对声传播的影响,即假设信号以平面波的形式传播时,单矢量水听器接收到的信号声压p和正交的二维振速Vx、Vy可以表示为

式中:x(t)为声压通道接收到的声压波形,θ为入射声波的水平方位角,θ的取值范围为0<θ<2π。即平面波时,第n个水声信号在矢量水听器上的阵列流型a(θn)可表示为a(θn)=[1cos(θn)sin(θn)]T。a(θn)的3个分量分别对应矢量水听器的声压通道以及Vx、Vy2个振速通道。
在远程方位估计问题中,不可避免需要考虑信道对方位估计结果的影响。在不能与实际声传播条件精确匹配的情况下,高分辨方位估计方法的分辨精度及稳定性将会出现下降,所以需要考虑水声信道对声传播的影响。在水声学中,波动理论是研究水声信号传播问题的重要方法之一。简正波处理方法主要研究简谐声信号的振幅和相位在声场中的变化,适用于低频浅海远距离的传播条件[9]。
根据简正波理论,将浅海看作具有自由平整界面,硬质海底,水深一定,水平不变的海洋模型,即声速、密度只与深度z有关。假定声源为各向同性的,海水为水平分层介质,假设激发M阶简正波,则声压场可表示为

式中:p(r,z,t)为声压,ρ(z)为介质的密度,Zm(zs)、Zm(zr)分别为第m阶简正波在声源和接收器深度的本征函数,km为第m阶简正波的本征值,为第一类Hankel函数,则单矢量水听器接收信号可表示为

式(4)可进一步写为

式中:A=[A1A2…AM]为扩展的导向矢量空间,对应的第m列即为矢量水听器的阵列流型a(θk)=[1cos(θk)sin(θk)]T。
B为加权因子,即简正波模型下矢量水听器接收信号的源矢量为:D=A×B。通过以上推导可得出简正波模型下矢量水听器接收到的信号为

2 矢量最优化算法
2.1 稳健性算法的提出
设当前扫描方位角为θt,根据空间位置关系,可得到该方向上实际的扩展导向矢量空间为A(θt),加权系数为B(θt),源矢量为D(θt);真实的扩展导向矢量空间为(θt),加权系数为(θt),源矢量为(θt)。考虑源矢量误差ΔNM的影响,将实际源矢量D(θt)重新表达为

ΔNM的范数可以由常数ε>0进行约束:

则实际的源矢量D(θt)将属于集合:
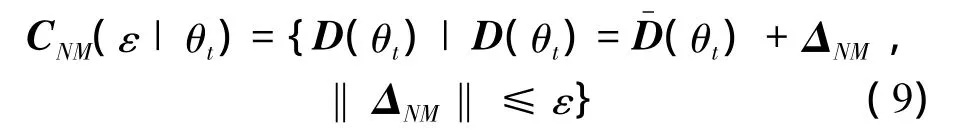
对属于集合CNM(ε|θt)的源矢量进行约束,即阵列响应的绝对值不小于1。

因此,稳健算法可以表示成约束最优问题[10-11]:

将矢量最优化约束优化问题与简正波模型相结合,提出了简正波模型的浅海稳健方位估计方法(NM-VORB),该方法对源矢量失配与有限采样效应等进行联合约束。该算法可表达为
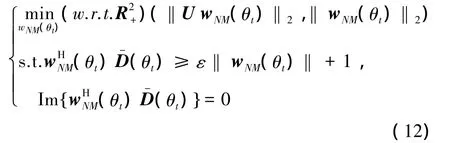
其中,U可由R进行Cholesky分解R=UHU得到。目标函数中的()表示在正实数域中讨论和的取值。式(12)为具有 2个目标函数和的 矢 量 最 优 化 问 题。 其 中,为惩罚项,其作用是在U存在扰动的条件下,使得原目标函数能够得到稳定的权矢量
2.2 稳健算法的Lagrange快速求解
根据Tikhonov正则化方法,式(12)同样可以表达为

其中,τ>0为约束参数。进一步对式(13)的约束函数进行化简:

利用Lagrange乘数法对上式进行求解,经推导可得最优权矢量可表示为

式中:为采样数据协方差矩阵,ξNM为最优对角加载因子,写为

2.3 稳健方位估计结果
将目标在t时刻时的最优权系数wNM(θt)代入目标函数(θt)R wNM(θt)中,可得在最优权系数下输出功率为

在感兴趣的角度范围进行谱峰搜索,即可得到单矢量水听器基于简正波模型的矢量最优化稳健波束形成空间谱图。
3 计算机仿真分析
3.1 窄带信号的方位估计
仿真的环境参数如图1所示:海水深度26 m,海水声速c1=1 517 m/s,c2=1 500 m/s。沉积层厚度2 m,声速c3=1 580 m/s,c4=1 600 m/s,密度1.6g/cm3,吸收系数α1=0.02 dB/λ。基底声速c4=1 700 m/s,密度 1.8 g/cm3,吸收系数α2=0.04 dB/λ。声源入水深度5 m,矢量水听器位于海底,声源距矢量水听器潜标的距离为 3 km,声源频率300 Hz。采样频率为3 000 Hz,采样快拍数6 000,搜索步长为 Δθ=0.1°,进行100次 Monte-Carlo实验。在该仿真条件下,利用简正波程序Kraken计算出共激发出5阶简正波。
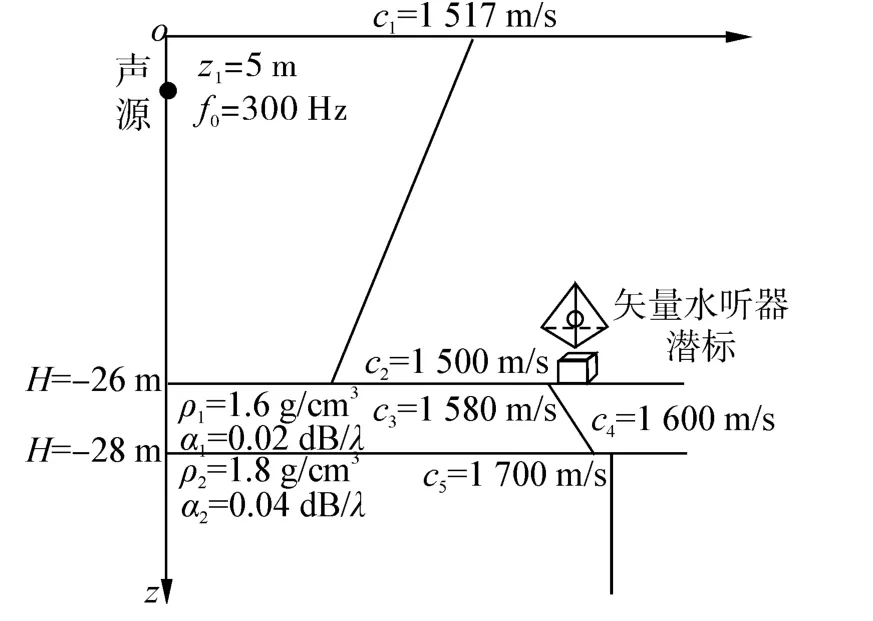
图1 仿真环境及矢量水听器潜标参数模型Fig.1 The simulation environment and vector submersible buoy parameter model
图2给出不同信噪比下窄带信号位于120°方向时4种方法的方位估计性能曲线。其中,NMCBF、NM-MVDR、NM-VORB分别为基于简正波模型的常规波束形成、最小方差信号无畸变波束形成和本文的矢量最优化波束形成(下同)。可以看出在信噪比大于5 dB时,4种方法的估计偏差都在1°以内,说明在具有一定的信噪比下,4种方法都可以对目标进行准确的方位估计。当信噪比小于-5 dB时,方位估计偏差和标准差显著增大,不能给出目标准确方向,说明该方法对信噪比有一定的要求。在本文仿真条件下,当信噪比大于-2 dB时基于单矢量水听器的高分辨方位估计方法和互谱法均能够有效地对目标进行方位估计,并且随着信噪比增高,方位估计的结果趋近于无偏估计。
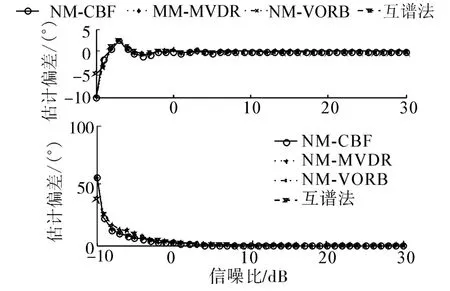
图2 不同信噪比下窄带信号方位估计性能Fig.2 The performance of DOA estimation of narrowband signals at different SNRs
表1给出不同信噪比(SNR)、不同入射角情况下4种方法的方位估计结果。将谱峰与最大旁瓣比(peak-to-sidelobe-ratio)表示为 PSR,-3 dB波束宽度表示为Θ-3dB。可以看出,4种方法的方位估计偏差都在1°以内,说明在较高的SNR情况下,这4种方法都可以准确的估计出目标的方位角,证明了算法的正确性和有效性。在相同的条件下,本文提出的矢量最优化算法具有更高的PSR以及更窄的Θ-3dB,方位估计性能最优。
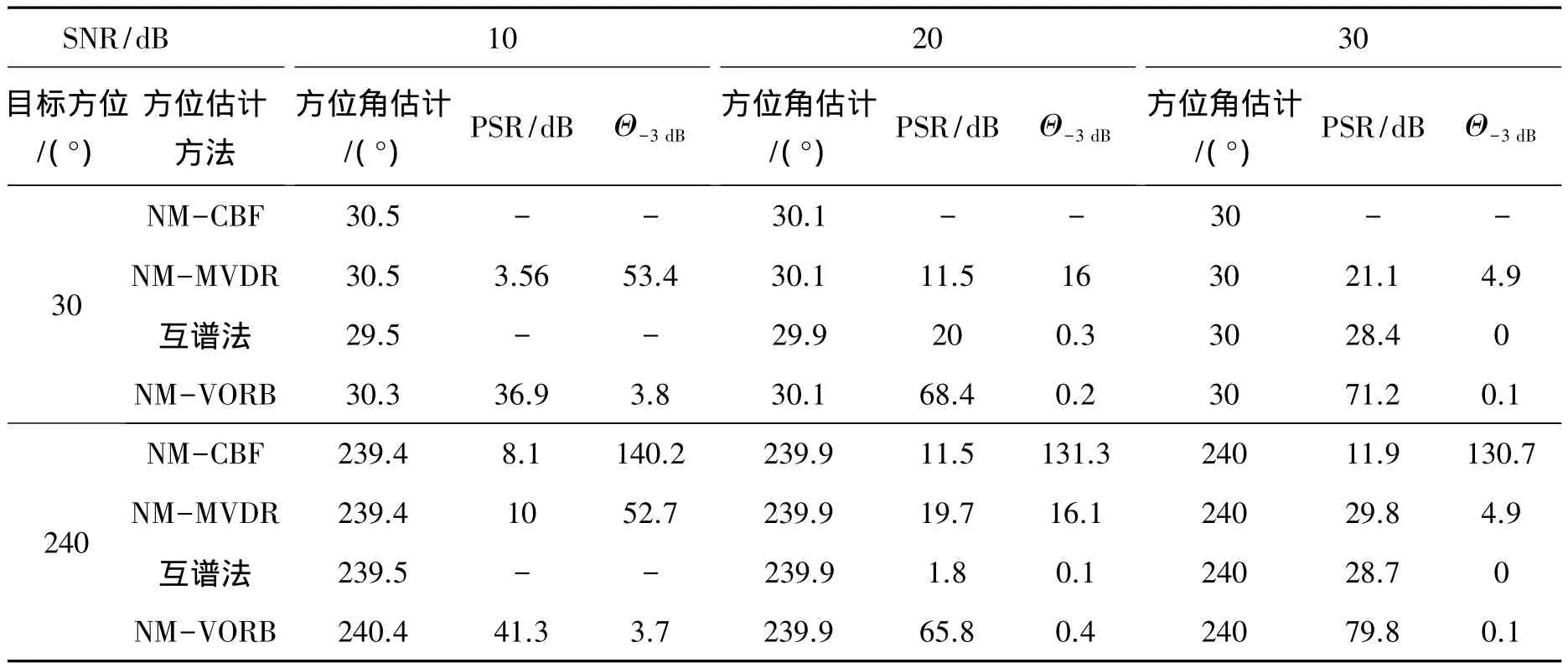
表1 不同入射角及信噪比条件下,4种方法的方位估计对比(窄带信号)Table 1 The performance of DOA estimation results of the four methods under different incidence angles and SNR(narrowband)
由图3的空间谱估计结果可以看出:1)尽管NM-CBF法可以估算出目标的方位角,但其空间谱主瓣很宽,旁瓣水平很高且背景起伏较大,总体性能很差;2)NM-MVDR的性能优于NM-CBF,但是旁瓣水平较高,稳健性容易受到环境失配的影响;3)互谱法的性能优于前2种方法,但是最大主旁瓣比不是很高且旁瓣不平滑;4)NM-VORB算法在相同的条件下,具有最为尖锐的谱峰和最大的主瓣与旁瓣比,保证较高方位估计精度的同时具有较高的背景抑制能力。综合不同信噪比以及不同的入射角情况均能够发现,在4种方法中,NM-VORB算法具有最为优秀的方位估计性能,给出最好的方位估计结果。
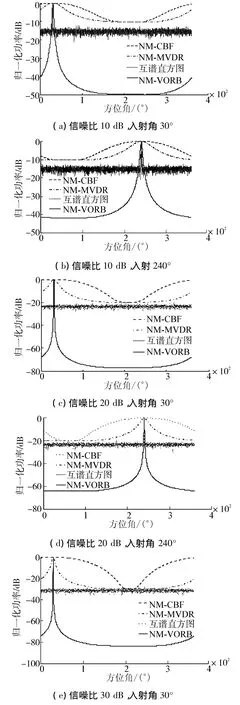
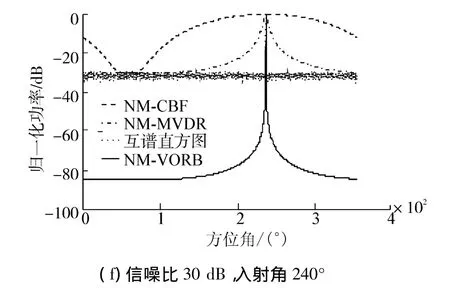
图3 不同信噪比、不同入射角4种方法的空间谱Fig.3 The spatial spectrum of the four different methods under different SNR and incidence angles
3.2 宽带信号的方位估计
仿真的环境参数与图1基本相同。矢量水听器位于海底,声源与矢量水听器潜标的距离为3 km,声源为50~1 000 Hz的宽带信号。采样频率为3 000 Hz,采样快拍数 6 000,Δθ=0.1°,进行100 次Monte-Carlo实验。在该仿真条件下,利用简正波程序Kraken计算出信号频带范围内共激发出950阶简正波。
图4给出不同信噪比下宽带信号位于120°方向时4种方法的方位估计性能曲线。可以看出,4种方法对于宽带信号和窄带信号的方位估计性能类似,在此不再赘述。

图4 不同信噪比下宽带信号方位估计性能Fig.4 The performance of DOA estimation of broadband signals at different SNRs
观察图5和表2可以发现,虽然相比于单频时的最大主旁瓣比有所降低,但是由于信号信息量的增加,其测量精度和算法的稳健性有所提高。本文提出的矢量最优化方法依然具有最尖锐的谱峰,其他方面与窄带信号的方位估计类似。需要指出的是传统的宽带信号阵列处理需要建立相应的频域模型,或是采用非相干信号子空间方法,即将宽带信号在频域上分成若干窄带信号,利用窄带的DOA估计方法估计方位,或是采用相干信号子空间方法,通过聚焦变换,将所有子带的能量映射到某一频段上,再参考窄带的DOA估计方法估计方位[12],而本文的单矢量水听器高分辨估计算法都是基于时域模型对宽带信号和窄带信号进行处理,避免了传统算法时频变换的过程,这也是单矢量水听器高分辨算法的一大优势。
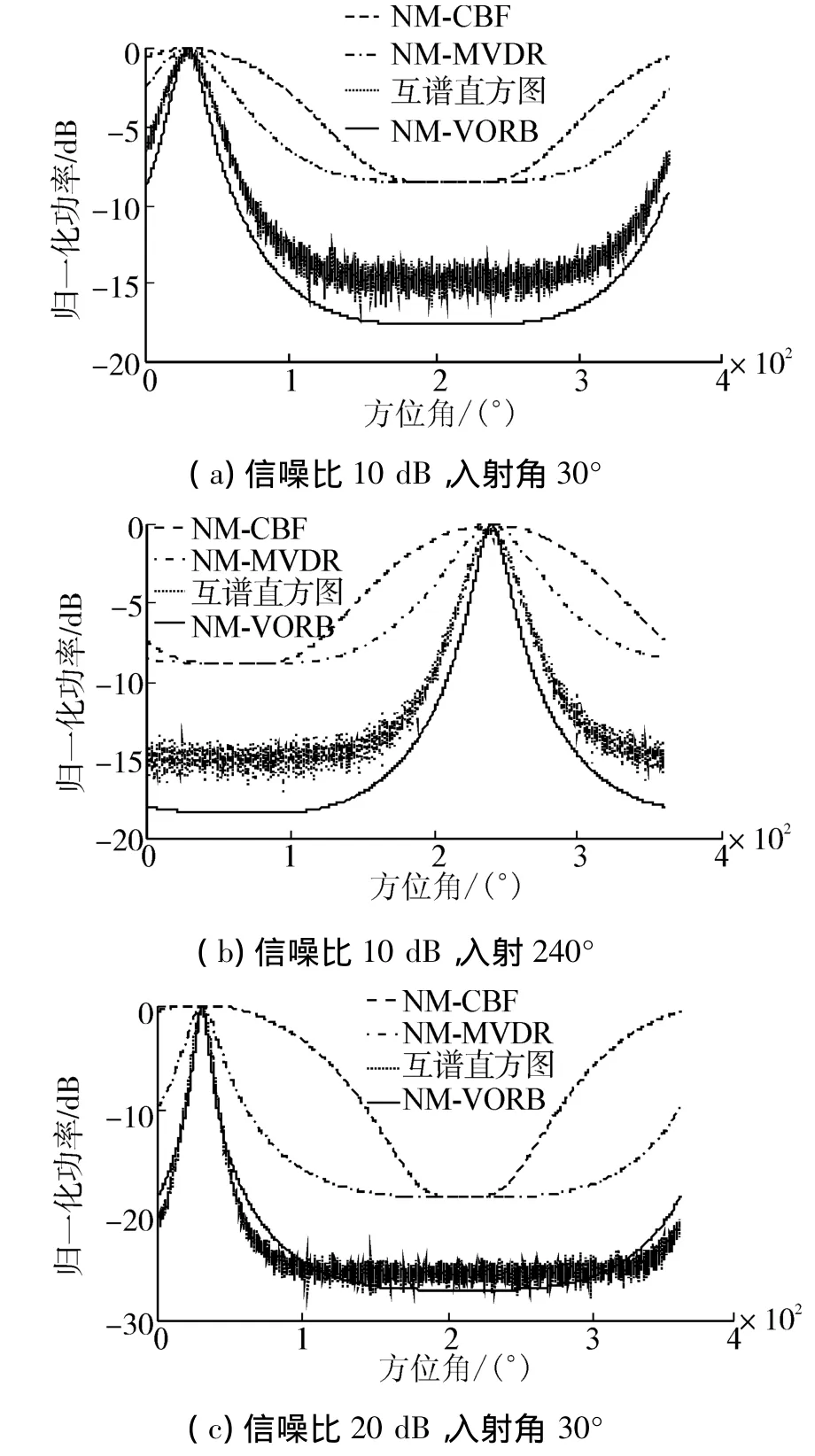

图5 不同信噪比、不同入射角4种方法的空间谱Fig.5 The spatial spectrum of the four different methods under different SNRs and incidence angles
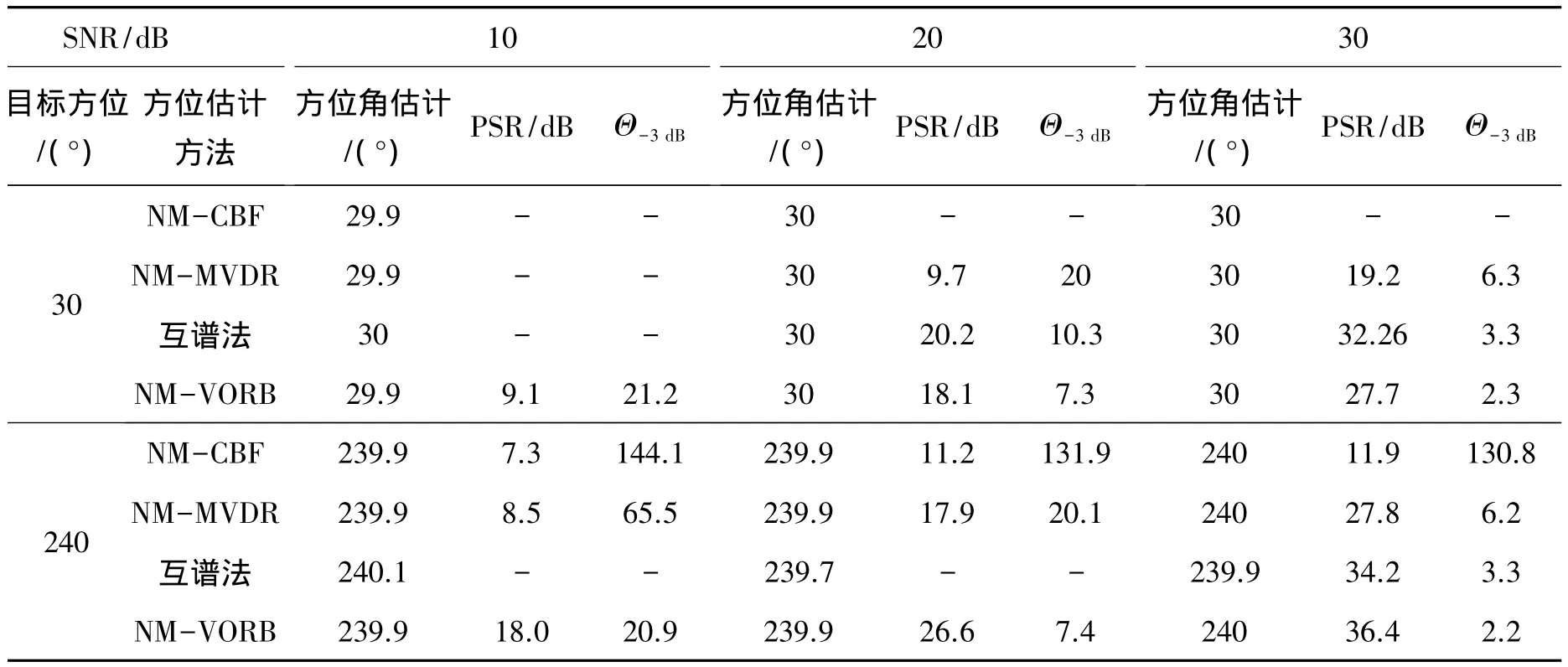
表2 不同入射角及信噪比条件下,4种方法的方位估计对比(宽带信号)Table 2 The performance of DOA estimation results of the four methods under different incidence angles and SNR(wideband)
4 海试数据分析
为了验证算法的有效性,处理了海上实验数据。实验中,目标是频率为300 Hz的单频信号、采样频率为10 kHz,搜索步长为Δθ=0.1°,海洋环境参数与仿真条件相同。
图6给出了3种方法处理相同0.2s数据得到的空间谱,NM-CBF、NM-MVDR、NM-VORB 3 种方法对目标方位的估计结果分别为 292.1°、293°以及292.9°,3种方法的方位估计结果与目标实际的方位很接近。
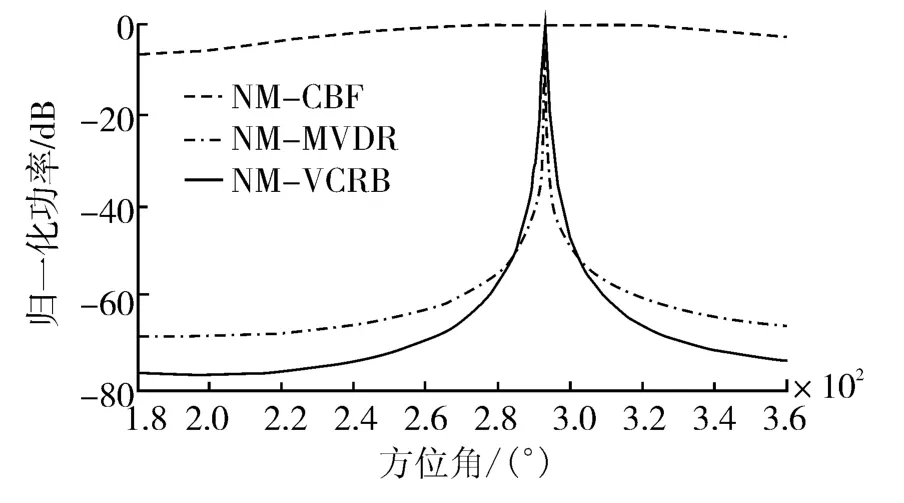
图6 3种方法处理海试数据得到的空间谱Fig.6 The spatial spectrum of the three different methods given by sea trial data
实验结果验证了单矢量水听器高分辨方位估计算法的有效性。与仿真情况相似,NM-CBF方法的空间谱谱峰很宽,性能很差。NM-MVDR与NMVORB均有很尖锐的空间谱,但是NM-VORB算法的PSR更大,在保证方位估计精度的同时有着更强的稳健性,总体性能依然是NM-VORB最优。
图7给出了处理5 s海试数据得到的瀑布图。
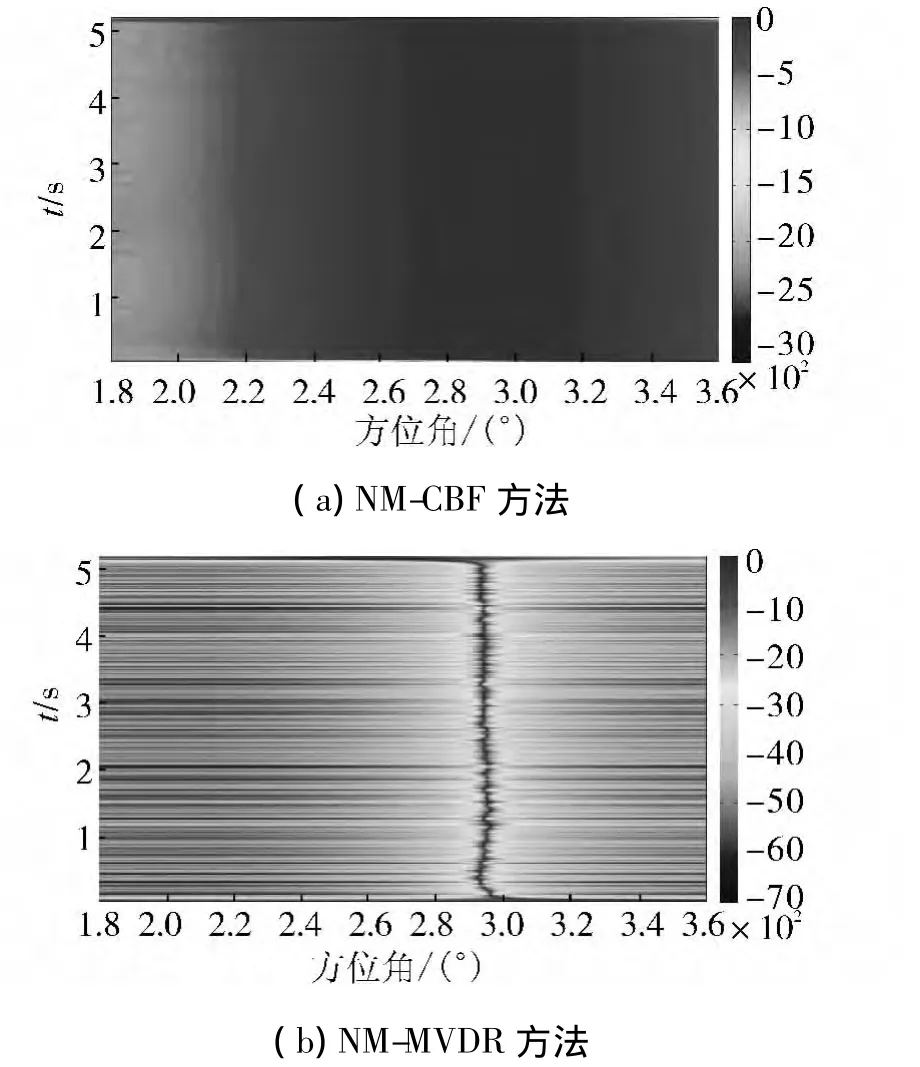

图7 4种方法处理海试数据得到的瀑布图Fig.7 The chat of waterfall of the four different methods given by sea trial data
从图7中可以看出实验结果与仿真结果很相似,本文提出的NM-VORB方法拥有更清晰的目标时间方位历程,海试数据的处理结果充分的验证了本文提出的单矢量水听器高分辨算法的有效性。
5 结束语
本文根据单矢量水听器阵列流型的特点,将稳健自适应波束形成的方法应用到单矢量水听器方位估计上,并且充分考虑信道对声传播的影响,用简正波理论构造单矢量水听器的接收模型,利用单个矢量水听器对浅海中目标进行方位估计,得出以下结论:
1)单矢量水听器可以对目标进行高分辨方位估计,并且在考虑信道影响的情况下,得到了较好的仿真和实验结果。
2)与传统的高分辨方法相比,基于简正波理论的单矢量水听器的矢量最优化算法具有更为尖锐的谱峰和更低的旁瓣水平,性能最佳。
3)在较低信噪比下,单矢量水听器高分辨方位估计的误差很大,如何提高在较低信噪比下的性能是以后的研究中需要解决的问题。
[1]孙贵青,李启虎.声矢量传感器信号处理[J].声学学报,2004,29(6):491-498.SUN Guiqing,LI Qihu.Acoustic vector sensor signal processing[J].Acta Acustica,2004,29(6):491-498.
[2]周士弘.分层介质波导中的声矢量场传播[J].哈尔滨工程大学学报,2004,25(1):38-42.ZHOU Shihong.Acoustic vector fields propagation in horizontal-stratified waveguide[J].Journal of Harbin Engineering University,2004,25(1):38-42.
[3]杨士莪.单矢量传感器多目标分辨的一种方法[J].哈尔滨工程大学学报,2003,24(6):591-95.YANG Shi’e.Method of multi_sources distinguishing by single vector transducer[J].Journal of Harbin Engineering U-niversity,2003,24(6):591-595.
[4]姚直象,惠俊英,殷敬伟,等.基于单矢量水听器四种方位估计方法[J].海洋工程,2006,24(1):122-127.YAO Zhixiang,HUI Junying,YIN Jingwei,et al.Four approaches to DOA estimation based on a single vector hydrophone[J].The Ocean Engineering,2006,24(1):122-127.
[5]NEHORAI A,PALDI E.Acoustic vector-sensor array processing[J].IEEE Transactions on Signal Processing,1994,42:2481-2491.
[6]惠俊英,惠娟.矢量声信号处理基础[M].北京:国防工业出版社,2009:57-60.
[7]王永良.空间谱估计理论与算法[M].北京:清华大学出版社,2004:22-23.
[8]WANG Yongliang.The theory and arithmetic of spatial spectrum[M].Beijing:Tsinghua University Press,2004:22-23.
[9]顾晓东,邱志明,袁志勇.单矢量水听器ESPRIT波达方向估计算法[J].哈尔滨工程大学学报,2009,30(8):867-871.GU Xiaodong,QIU Mingzhi,YUAN Zhiyong.ESPRIT algorithm for DOA estimation using a single vector hydrophone[J].Journal of Harbin Engineering University,2009,30(8):867-871.
[10]杨士莪.水声传播原理[M].哈尔滨:哈尔滨工程大学出版社,2007:26-28.
[11]VOROBYOV S A,GERSHMAN A B,LUO Z Q.Robust adaptive beamforming using worst-case performance optimization:a solution to the signal mismatch problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.
[12]宋海岩.具有高稳健型的浅海目标方位估计方法研究[D].哈尔滨:哈尔滨工程大学,2012:34-38.SONG Haiyan.Research on robust bearing estimation method in shallow water[D].Harbin:Harbin Engineering University,2012:34-38.
[13]梁国龙,张锴.单矢量水听器的高分辨方位估计应用研究[J].兵工学报,2011,32(8):986-990.LIANG Guolong,ZHANG Kai.Research on high-resolution direction-of-arrival estimation based on an acoustic vectorhydrophone[J].Acta Armamentarii,2011,32(8):986-990.

