一种水平蒸汽发射系统的基本性能优化设计
严志腾,金家善,朱 泳
(海军工程大学动力工程学院,湖北武汉430033)
一种水平蒸汽发射系统的基本性能优化设计
严志腾,金家善,朱 泳
(海军工程大学动力工程学院,湖北武汉430033)
针对水平蒸汽发射系统各组成部分参数相互耦合的问题,应用变质量热力学理论,建立了水平蒸汽发射系统各组成部分的动态数学模型,并对系统的发射过程进行了动态仿真,分别得到了3种不同类型发射阀下的流量系数与载荷无量纲速度随无量纲位移变化曲线之间的对应关系,在此基础上,对系统发射性能进行了分析和优化设计,进而得到了优化后3种不同类型发射阀的流量系数及系统相关参数之间的关系,为系统的设计和试验提供了理论指导。
水平蒸汽发射系统;发射阀;性能分析;优化设计;流量系数
水平蒸汽发射系统是一类实现蒸汽内能向载荷动能转换的弹射动力系统,其工作原理类似于舰载蒸汽弹射系统[1],也是以高压水蒸汽作为动力源的弹射动力系统。而按照动力源的不同,目前还有分别以高压气体[2-3]和燃气、蒸汽的混合工质[4]为动力源的弹射动力系统。
近年来,许多学者对以高压气体或燃气、蒸汽的混合工质等为动力源的弹射动力系统进行了优化设计[5-7],而对于以蒸汽为动力源的弹射动力系统,虽然也有些学者对其进行了建模仿真研究[1],但在系统的优化设计方面,目前还没有相关的研究成果报道。因而本文便对系统进行了性能分析和优化设计,以期得到最优的系统发射性能。
1 系统结构及原理
水平蒸汽发射系统主要由蒸汽蓄热器、发射阀、汽缸、活塞组件、载荷等部件以及连接它们所布置的蒸汽管路组成,其基本构成如图1所示。图中,P0为蒸汽蓄热器内湿蒸汽压力,MPa;T0为蒸汽蓄热器内温度,℃;h0为蒸汽蓄热器内工质的比焓,kJ/kg;ρ0蒸汽蓄热器内密度,kg/m3;V0为蒸汽蓄热器内体积,m3;a蒸汽蓄热器内充水系数;上标′和″分别代表湿蒸汽的水部和汽部参数;Q为瞬时放汽流量,kg/s;Pc为汽缸内压力,MPa;hc为汽缸内工质的比焓,kJ/kg;ρc为汽缸内密度,kg/m3;Vc为汽缸内体积,m3;Dp为活塞直径,mm;mp、mf分别为活塞组件和载荷的质量,kg;AP为蒸汽作用到活塞组件上的有效横截面积,m2;Ff为汽缸内壁的摩擦力,N;N为汽缸支持力。
系统中蒸汽蓄热器是在极短时间内为载荷提供规定压力和数量蒸汽的储能设备,其下部为水空间,上部为汽空间[8]。在运行时,通过发射阀的控制,蒸汽蓄热器汽部饱和蒸汽在极短时间内由蒸汽管路大量充入汽缸,汽缸内蒸汽膨胀经由活塞组件对载荷做功,从而推动两者向前做加速运动,最终达到规定的位移,并在该位移下同时满足规定的速度要求。

图1 水平蒸汽发射系统基本构成图Fig.1 Basic structure chart of horizontal steam-launch system
2 系统的动态数学模型
在建立系统各子模块的数学模型之前,还需在允许的范围内给出以下假设条件:
1)放汽过程中,蒸汽热力状态变化过程视为准平衡过程,且忽略蒸汽的宏观动能和蒸汽在管路流动中的阻力;
2)蒸汽蓄热器为刚性容器,内部参数采用集总参数法处理;
3)由于蒸汽蓄热器和管路外都敷有保温层,且放汽时间极短,故忽略工质与外界的换热,包括蒸汽蓄热器与蒸汽之间的换热等;
4)假设发射阀刚开启前,汽缸余隙容积内的蒸汽处于一定压力Pc0和汽缸预热温度Tc0条件下的热力状态;
5)忽略汽缸内蒸汽与汽缸之间的换热,以及汽缸中初始空气的影响;
6)忽略汽缸内蒸汽的漏泄;若汽缸内蒸汽存在湿蒸汽状态,则忽略蒸汽中冷凝水所占的体积;
7)假设活塞组件和载荷是刚体且不发生变形、不影响力的作用点(线)的宏观变化。
2.1 蒸汽蓄热器热力学模型
取蒸汽蓄热器空间作为一个控制容积来进行热力学分析,该控制容积内工质状态变化规律同时满足质量守恒方程、能量守恒方程和体积守恒方程[9]。
控制容积内工质满足质量守恒方程:

控制容积内工质满足能量守恒方程:
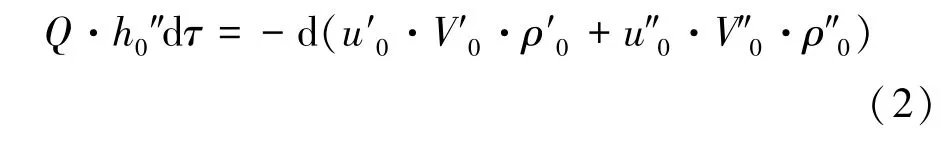
式中:u0为工质比热力学能,kJ/kg。
该控制容积内工质同时满足体积守恒方程:
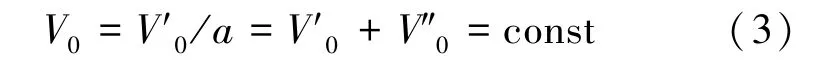
蒸汽蓄热器的累积放汽量可表示为

根据水和水蒸气热力性质可知,蒸汽蓄热器内湿蒸汽的汽部和水部状态函数都仅是压力或温度的单值函数,都可用水和水蒸气热力计算函数[10]得出:
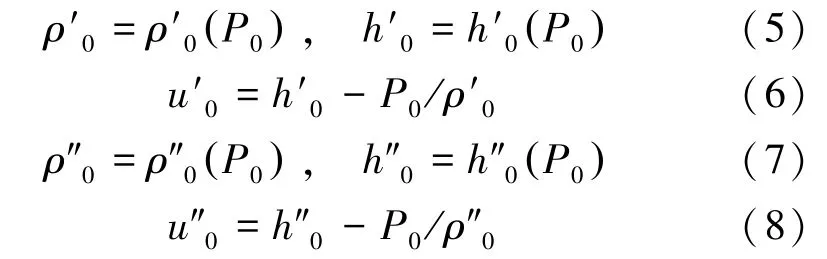
2.2 发射阀流量特性模型
针对系统中发射阀的研究,主要从对数、直线和快开调节阀这3种常见类型进行分析。
工质流经调节阀的流动主要分为阻塞流和非阻塞流2种情况,而在系统中,流经发射阀的工质为干饱和蒸汽,是可压缩流体。对于可压缩流体,一般用临界压差比XT与比热比系数FK的乘积作为产生阻塞流的临界条件[11]。
当X≥FK·XT时,为阻塞流[11]:
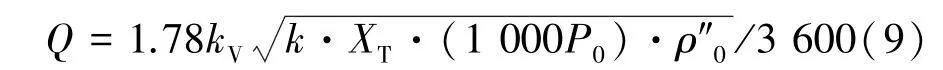
式中:X为压差比,X=(P0-Pc)/P0(Pc为汽缸内压力,MPa);FK=k/1.4(k为蒸汽的绝热指数,蒸汽过热时k=1.3;蒸汽饱和时k=1.135);XT的数值只决定于阀的流路情况及结构;kv为对应于发射阀某一开度下的流量系数,表征调节阀的流通能力。
当X<FK·XT时,为非阻塞流[11]:

式中:y为膨胀系数,y=1-X/(3 FK·XT)。
2.3 汽缸热力学模型
取汽缸内容积为控制容积来进行热力学分析,该控制容积内工质状态变化规律同时满足质量守恒方程和能量守恒方程。
控制容积内工质满足质量守恒方程:

式中:Vc0为初始时刻汽缸的余隙容积;x为活塞组件及载荷的位移,m。
能量守恒方程为

式中:uc为汽缸内蒸汽比热力学能,kJ/kg。
汽缸内水蒸汽状态参数为压力和密度的函数,都可用水和水蒸气热力计算函数[10]得出:

2.4 活塞组件和载荷动力学模型
活塞和载荷的受力分析如图1所示。
活塞组件和载荷沿加速度方向的运动方程为

至此,由以上方程(1)~(17)联立所组成的方程组,即为水平蒸汽发射系统的动态数学模型。通过该模型对系统放汽过程进行数值仿真,就可得到相应的系统性能参数随时间变化规律,进而通过系统相关输入参数的调整,对系统进行性能分析和优化设计。
3 系统性能分析及优化设计
3.1 系统的数值仿真和性能分析
给定发射阀的开阀规律为线性开阀(即在规定的放汽时间下,阀相对开度从0开度线性增加到最大开度1)条件下,对系统的放汽过程进行数值模拟,便可得不同Kv值的发射阀下,载荷无量纲速度w∗随无量纲位移x∗变化的系统性能曲线,如图2~4所示,用于系统数值仿真计算所用的主要参数如表1所示。其中,w∗和x∗的取值范围都在0~1。
在图2~4的每个图中,所给出的3条实线都分别代表了3种不同Kv值下载荷无量纲速度w∗随无量纲位移x∗变化曲线;点划线则为所有不同的Kv值下,系统放汽结束时载荷所能达到的位移及对应速度的点所连成的曲线;而载荷需在规定的无量纲位移x∗内达到规定无量纲速度w∗的系统使用要求,则在图中用空心圆点来表示,该点的坐标(x∗,w∗)取值为(0.82,0.9)。由此可以看出,每个图中的点划线左侧区域,即为系统放汽过程中,载荷所能到达的无量纲位移x∗和对应的无量纲速度w∗的点集区域。
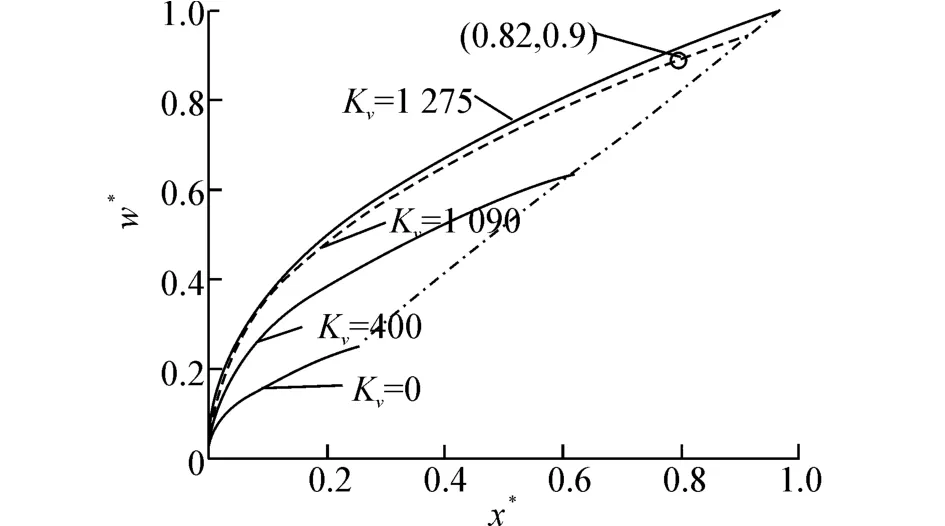
图2 直线调节阀下载荷速度与位移之间关系曲线Fig.2 The relation curve between load speed and displacemen of the linear regulator

图3 对数调节阀下载荷速度与位移之间关系曲线Fig.3 The relation curve between load speed and displacemen of the logarithmic regulator

图4 快开调节阀下载荷速度与位移之间关系曲线Fig.4 The relation curve between load speed and displacemen of the quick opening valve
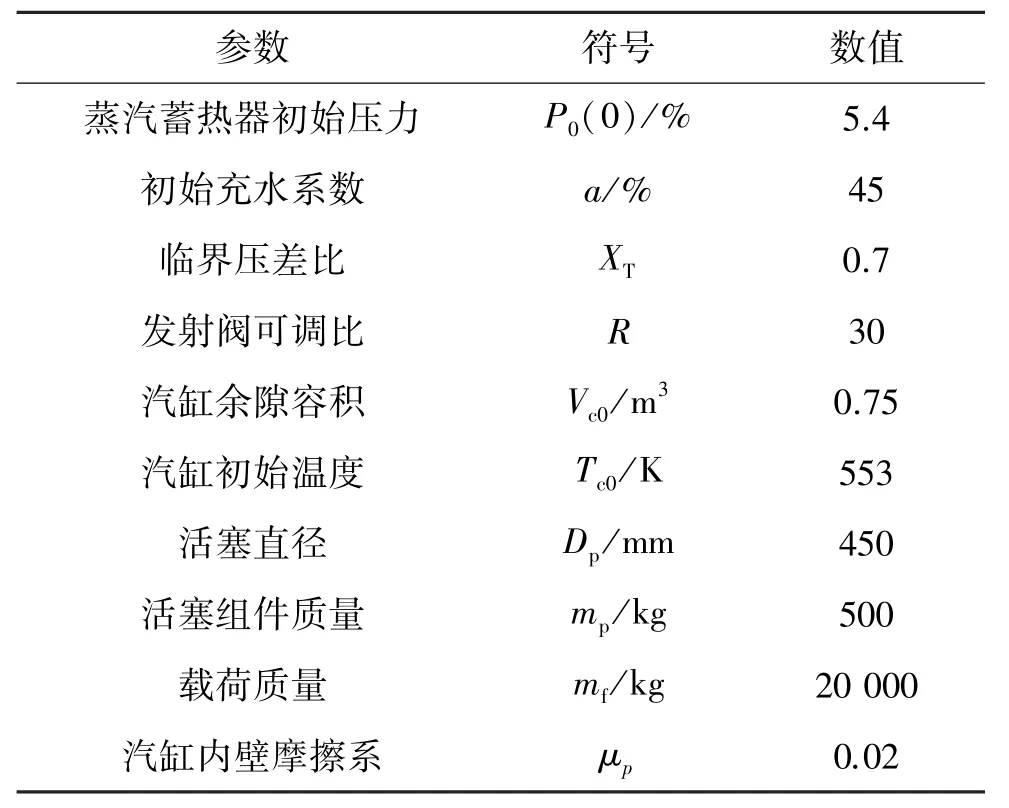
表1 主要仿真参数Table 1 Main simulation parameters
另外还需注意的是,当发射阀Kv值趋近于0时,由蒸汽蓄热器流入汽缸的蒸汽流量也趋近于0,然而从图2~4中都可以看出,由系统的仿真计算得出载荷位移却并不趋近0,在3种不同类型调节阀下x∗皆为0.27。这是因为系统的仿真计算是基于汽缸在蒸汽蓄热器放汽前的极短时间内已充入了一定量蒸汽(即该余隙容积空间存在着假定的压力Pc0和温度Tc0)的初始条件下进行的,而如果Kv值趋近于0,会造成发射阀的流通能力过小,使得汽缸已无法在蒸汽蓄热器放汽前的极短时间内充入足够的蒸汽,从而造成该余隙容积空间达不到假定的压力Pc0和温度Tc0,故该假设条件将不再适用,需要进行修正。但在对系统进行优化设计的过程中发现,发射阀的Kv值都在初始条件的适用范围内,因此仍然可以借助图4~6所给出的载荷无量纲位移x∗和无量纲速度w∗的点集区域,对3种不同类型调节阀下系统的优化设计开展研究。从图2~4中可以看出,在点集区域内,发射阀Kv值选得越大,相同的无量纲位移下载荷所能达到的无量纲速度也越大;随着发射阀Kv值的增大,在系统放汽过程结束时,载荷所能达到的无量纲位移和无量纲速度也在
同时增大;在直线调节阀和快开调节阀下,代表着系统使用要求的空心圆点落在了点集区域内(分别如图4和图6所示),而在对数调节阀下,该空心圆点则落在了点集区域外(如图5所示)。显然,如果空心圆点落在点集区域内,则表明存在着某一Kv值,使得载荷在无量纲位移x∗为0.82时,其所达到的无量纲速度w∗恰好为0.9,从而使得系统的发射性能达到最优;反之,如果空心圆点落在点集区域外,则选取任何的Kv值,都无法使载荷在无量纲位移x∗为0.82时,其所达到的无量纲速度w∗恰好为0.9。因此,在无量纲位移x∗为0.82时,载荷所能达到的最小无量纲速度,即对应着系统所能达到的最优发射性能。显然,坐标为(0.82,)的点正好落在系统放汽结束时载荷所能达到的位移及对应速度的点所连成的曲线,即点划线上。
3.2 优化设计结果分析
通过3.1节的分析可知:在直线和快开调节阀下,当Kv值分别为1 090和825时,载荷在位移为0.82时,其无量纲速度刚好为0.9,即系统在这一发射性能上达到了最优;而在对数调节阀下,当Kv值为2 450时,载荷所能达到的速度超过规定值额度最小,此时,载荷的无量纲位移为0.82时,其无量纲速度为0.91。显然,对于优化后的系统,当发射阀选用对数调节阀时,调节阀口径最大,直线调节阀的口径次之,而快开调节阀的口径最小。
优化后3种不同类型发射阀下,无量纲累积放汽量及蒸汽蓄热器无量纲压力随载荷无量纲位移变化曲线如图5所示,同时可得载荷无量纲加速度随无量纲时间变化曲线如图6所示。

图5 累积放汽量及蒸汽蓄热器内压力随载荷位移之间关系曲线Fig.5 Cumulative discharge of steam and steam accumulator pressure varies with the load displacement
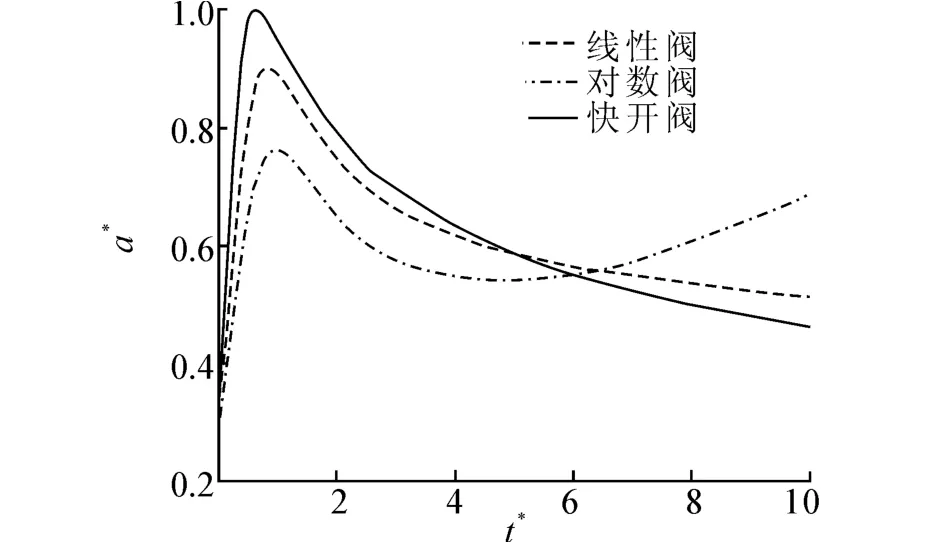
图6 载荷加速度随时间变化曲线Fig.6 Curves of load acceleration varies with time
图5可以看出:当载荷位移较小时,在相同的载荷无量纲位移下,快开调节阀下累积放汽量最大,直线调节阀下次之,对数调节阀下最小,对应的快开调节阀下蒸汽蓄热器内无量纲压力下降最快,直线调节阀下次之,对数调节阀下最慢;随着载荷的位移不断增加,在相同的无量纲位移下,对数调节阀下累积放汽量最大,直线调节阀下次之,快开调节阀下最小,对应的对数调节阀下蒸汽蓄热器内无量纲压力下降最快,直线调节阀下次之,快开调节阀下最慢。当载荷位移为0.82时,直线、对数和快开调节阀下累积放汽量分别为0.62、0.83和0.56。显然,在对数调节阀下,系统需消耗最多的蒸汽量,才能使载荷在规定的位移达到规定的速度,而直线调节阀下所需消耗的蒸汽量次之,快开调节阀下最小。
图6可知,对数、直线和快开调节阀下载荷加速度的波动幅度依次增大,经计算,载荷加速度峰均比分别为1.27、1.46和1.60。
4 结论
1)通过建立水平蒸汽发射系统的动态数学模型,在给定发射阀开阀规律为线性开阀的情况下,得到了发射阀流量系数与载荷无量纲速度随无量纲位移变化曲线之间的对应关系。
2)依据仿真得到的发射阀流量系数与载荷无量纲速度随无量纲位移变化曲线之间的对应关系,对系统进行了优化。结果表明,当直线调节阀和快开调节阀的最大流量系数分别为1 090和825时,载荷在规定的位移内能够刚好达到规定的速度,而在对数调节阀下,当载荷达到规定的位移时,其所能达到的最小的无量纲速度为0.91,稍高于规定的速度,此时,发射阀的最大流量系数为2 450。
3)优化后,直线、对数和快开调节阀下载荷加速度峰均比分别为1.46、1.27和1.60。
[1]程刚,倪何,孙丰瑞.舰载蒸汽弹射系统建模与仿真研究[J].武汉理工大学学报:交通科学与工程版,2010,34(2):301-305.
CHENG Gang,NI He,SUN Fengrui.Modeling and simulation research on naval steam-power aircraft launch system[J].Journal of Wuhan University of Technology:Transportation Science and Engineering,2010,34(2):301-305.
[2]戴龙成,宣益民,尹健.弹射装置的数理建模和动力学分析[J].弹道学报,2001,13(4):17-23.
DAI Longcheng,XUAN Yimin,YIN Jian.Modeling and dynamic analysis of nitrogen launching system[J].Journal of Ballistics,2001,13(4):17-23.
[3]练永庆,王树宗,陈一雕.气动式水下武器发射器内弹道优化研究[J].弹道学报,2002,14(2):1-5,12.
LIAN Yongqing,WANG Shuzong,CHEN Yidiao.Optimal study on the under water weapon’s interior of compressedair launcher[J].Journal of Ballistics,2002,14(2):1-5,12.
[4]CHEN Qinggui,ZHOU Yuan,WANG Haiyang,et al.Submarine-launched cruise missile ejecting launch simulation and research[C]//Proceedings of the 2011 IEEE International Conference on Electronic and Mechanical and Information Technology.Harbin,China,2011:4542-4545.
[5]廖振强,王涛,何大平,等.抛放弹弹射机构优化设计[J].南京理工大学学报,2002,19(3):259-263.
LIAO Zhenqiang,WANG Tao,HE Daping,etal.Optimization of blank cartridge ejection device[J].Joural of Nanjing University of Science and Technology,2002,19(3):259-263.
[6]陈庆贵,齐强,周源,等.发射动力系统内弹道优化设计计算[J].舰船科学技术,2003,27(5):573-577.
CHEN Qinggui,QI Qiang,ZHOU Yuan,et al.Interior trajectory optimization design and computation of launching power system[J].Ship Science and Technology,2003,27(5):573-577.
[7]戴龙成,宣益民,尹健.氮气作动筒结构参数的优化设计[J].弹道学报,2002,14(1):73-76,83.
DAI Longcheng,XUAN Yimin,YIN Jian.Optimization of pneumatic device system[J].Journal of Ballistics,2002,14(1):73-76,83.
[8]胡继敏,金家善,严志腾.汽源参数变化对储汽筒充汽系统变工况性能的影响[J].海军工程大学学报,2012,24(5):102-107.
HU Jimin,JIN Jiashan,YAN Zhiteng.Influence of the change of steam source paramters on the variable operating status characteristics ofseam accumulator system[J].Journal of Naval University of Engineering,2012,24(5):102-107.
[9]HU Jimin,JIN Jiashan,YAN Zhiteng.Fluid-solid coupling numerical simulation of charge process in variable-mass thermodynamic system[J].Journal of Central South University,2012,19(4):1063-1072.
[10]WAGNER W,COOPER J R,DITTMANN A,et al.The IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam[J].Journal of Engineering for Gas Turbines and Power,2000,122(1):150-182.
[11]吴国熙.调节阀使用与维修[M].北京:化学工业出版社,1999:101-114.
WU Guoxi.Operation and maintenance of control valve[M].Beijing:Chemical Industry Press,1999:101-114.
Optimal design of fundamental performance of the horizontal steam-launching system
YAN Zhiteng,JIN Jiashan,ZHU Yong
(College of Power Engineering,Naval University of Engineering,Wuhan 430033,China)
Focusing on the intercoupling of the parameters of each component of the horizontal steam-launching system,and based on the variable-mass thermodynamic theory,the dynamic mathematical model for each component of the system was established.In addition,a dynamic simulation ofthe launching process ofthe system was conducted and the corresponding relations between the flow coefficient,and the load dimensionless velocity and the dimensionless displacement variation curve under three kinds of different launching valves were respectively attained.On this basis,the performance of the system was analyzed and the optimal design of the system was carried out.Subsequently,the relations between the flow coefficientand the correlative parameters ofthe system under the three kinds of different launching valves were acquired.The results provide a theoreticalguidance for the design and experiment of the system.
horizontal steam-launching system;launching valve;performance analysis;optimal design;flow coefficient
10.3969/j.issn.1006-7043.201212026
TP202+.7
A
1006-7043(2014)02-0184-05
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201212026.html
2012-12-09.网络出版时间:2014-1-2 14:52:52.
严志腾(1986-),男,博士研究生;
金家善(1962-),男,教授,博士生导师.
金家善,E-mail:yan108zhi@163.com.

