高速切削锯齿形切屑形成过程的有限元模拟
段春争,王肇喜,李红华
(大连理工大学机械工程学院精密与特种加工教育部重点实验室,辽宁大连116024)
高速切削锯齿形切屑形成过程的有限元模拟
段春争,王肇喜,李红华
(大连理工大学机械工程学院精密与特种加工教育部重点实验室,辽宁大连116024)
为了研究和预测高速切削切屑形成过程,使用有限元分析软件ABAQUS建立了高速切削高温合金的有限元模型,采用Johnson-Cook热粘塑性材料本构模型、剪切损伤切屑分离准则以及刀-屑界面粘结-滑移混合摩擦模型,对高速切削高温合金过程中锯齿形切屑的形态及切削力进行了研究。通过模拟与实验的对比分析,验证了有限元模型的准确性。切削参数对切屑形成的影响的研究结果表明,高速切削过程中锯齿形切屑的锯齿化程度、切削力以及绝热剪切带内的等效塑性应变随切削速度、刀具前角以及切削厚度的改变而规律性地变化。
高速切削;有限元模拟;锯齿形切屑;高温合金;本构模型;切屑分离准则
高速切削是一个涉及高弹塑性变形和高切削温度的复杂过程。与传统切削在加工机理方面相比,高速切削常会产生锯齿形切屑。锯齿形切屑的形成导致切削力与切削热周期性波动,加快了刀具的磨损速率,降低刀具寿命和加工质量。因此,研究锯齿形切屑的形成机理对于优化高速切削过程具有重要意义。目前,主要有实验和有限元模拟2种方法。很多学者通过实验方法对高速切削锯齿形切屑的形成过程进行了深入研究[1-4]。大量的实验结果表明锯齿形切屑的形成机理主要分为绝热剪切理论和周期性断裂理论。多数学者认为,锯齿形切屑的形成原因是由于第一变形区内的剪切变形高度局部化,使第一变形区温度急剧升高,造成材料热软化效应超过加工硬化效应,剪切区内发生局部剪切断裂。虽然通过实验研究切削机理是一种可靠的方法,但高速切削实验条件复杂,并且很难在切削过程中准确获得切削温度、应力、应变等数据[5]。因此,采用有限元技术与实验相结合的方法成为研究和预测切削过程的一种有效手段,通过有限元模拟能够获得更多有效数据,从而提高研究结果的准确性。
创建高速切削有限元模型时,关键问题是能否合理地确定材料本构模型,切屑分离准则以及刀-屑摩擦模型。高速切削过程是非线性且十分复杂的材料去除过程,其中第一变形区的材料承受大的应变和应变率及很高的温升,因此,材料特性只能用热粘塑性本构模型描述[5-8]。高速切削过程中,必须采用物理准则作为切屑分离准则,以使模拟结果不因切削条件改变而变化。刀-屑界面上的摩擦会明显影响高速切削过程中切屑的形成机理,应该采用精确的模型来描述刀-屑界面的摩擦状态。
本文使用ABAQUS有限元分析软件建立了高速切削高温合金的正交切削有限元模型,对高温合金在不同切削参数下的锯齿形切屑形态和切削力进行了预测,并通过与实验结果的对比,验证了模型的准确性。
1 高速切削有限元模型的建立
1.1 几何模型的建立
在切削建模过程中,考虑到切削宽度远大于切削厚度,因此将切削过程简化为二维平面应变问题来处理[6]。如图1所示,工件网格采用4节点平面应变双线性热力耦合减缩积分单元(CPE4RT)进行离散处理。刀具网格为3节点平面应变三角形线性热力耦合单元(CPE3T)。为了在模拟的最后阶段,计算结果能够更好的收敛,切削层的网格相对切削平面倾斜45°[7]。

图1 金属切削加工有限元模型Fig.1 Finite element model of metal cutting
1.2 材料本构关系
普通切削速度下,金属切削过程的模拟常采用热弹塑性本构模型,但是,高速切削时,工件材料在高温、大应变和大应变率的情况下发生塑性变形,因此必须综合考虑各因素对工件材料流动应力的影响。本文采用包含了温度效应和应变率强化效应的Johnson-Cook热粘塑性材料本构模型,该本构关系的模型常数是通过使用分离式霍普金森杆的高速变形试验获得的,适合于材料在较大应变率范围内变形的情况,并且温度升高是由塑性变形导致的。高速切削加工过程中切屑第一变形区内的材料变形是一个典型的高速变形过程,因此该本构模型适用于高速切削过程的模拟,模型使用式(1)等效流动应力:


表1 GH4169高温合金Johnson-Cook模型中的材料参数Table 1 Johnson-Cook behavior law parameters of GH4169
1.3 刀-屑接触摩擦模型
传统切削加工的模拟中,普遍采用库伦摩擦理论描述刀-屑界面之间的摩擦。而高速切削中,刀-屑接触面间的材料发生微观改变,例如绝热剪切、相变甚至熔化等,前刀面上的正应力和温度会迅速增加。当前刀面上的正应力超过一定极限后,传统的库伦摩擦理论就不能准确地反映刀-屑接触面之间的摩擦状态以及工件与刀具间的摩擦应力与正应力的关系。
Zorev等的实验研究表明,高速切削时刀具与切屑的摩擦表面可划分为2个区域[5,8,10]:滑移区和粘结区。在滑移区,服从库伦摩擦定律;在粘结区,刀-屑接触点处的摩擦剪应力等于极限剪切应力。本文采用了粘结-滑移混合摩擦模型来描述刀-屑接触面之间的摩擦,整个刀-屑接触区域可描述为

式中:τf为摩擦应力,σn为法向应力,kchip为切削材料的极限剪切应力,μ为摩擦系数。当μσn≥kchip为粘结摩擦区,当μσn<kchip为滑动摩擦区。
1.4 切屑分离准则
目前切屑和工件的分离准则主要有几何分离准则和物理分离准则2大类。几何分离准则主要是通过刀尖与分离线之间的临界距离来判断切屑是否分离,不能很好地反映被加工材料的物理性质。而物理分离准则是通过一些特定物理量的数值是否达到临界值来判断,因此更符合实际的金属切削过程。由于高速切削高温合金过程中,切屑变形非常大,材料的剪切应变率很高,刀尖处发生严重的剪切损伤,此时,使用剪切损伤准则能更准确地反映切屑与工件材料的分离断裂情况。
剪切损伤(shear damage)准则是根据单元积分点处的等效塑性应变进行定义的,当被切削材料某一点处的等效塑性应变达到材料本身的等效塑性断裂应变时,就认为材料发生失效。该断裂准则假设断裂初始时的等效塑性应变为剪切应力比和应变率综合作用的结果,即:θ()。其中,θs=q+ksp()/τmax为剪切应力比,τmax为最大剪切应力,ks为材料参数。当满足式(3)时,发生初始断裂。
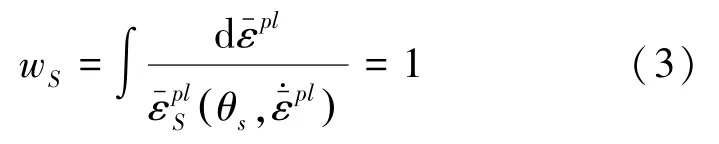
式中:wS是一个单调增加的状态变量,它随着等效塑性应变增量的变化而变化,当wS达到1时,断裂发生,此时材料单元被从网格中删除,实现切屑与工件的分离。
目前,使用有限元方法研究金属切削过程,为了使切屑与工件更好地分离,建模时经常设置一层独立于工件和切屑的分离线,这与实际的切削情况不相符[11]。本文在建模时,没有设置分离线,而是在工件与切屑接触区设置了一层切削损伤区,该损伤区与工件和切屑成为一个整体,如图2所示。此种方法消除了设置分离线造成的人为误差,更符合高速切削过程中刀具与切屑的实际接触情况。

图2 工件模型上的损伤区Fig.2 Damage zone in the workpiece
2 高速切削实验
实验在CA6140A车床上采用车削端面的方法对GH4169高温合金进行加工,属于典型的正交切削,刀具材料为硬质合金(YD201)。实验参数与有限元模拟的参数相同,切削速度的范围为10~300 m/min,切削厚度分别为0.07、0.10、0.15 mm,刀具前角γ0分别为-10°、0°、10°。切削过程中,使用压电式测力仪测量切削力并收集切屑。将不同切削条件下获得的切屑垂直嵌入由环氧树脂和固化剂按一定比例混合成的溶液中,固化后再经过研磨、抛光和腐蚀,获得高温合金切屑的金相表面,使用LEICA MEF4A型金相显微镜对切屑的微观形貌进行观察。
2.1 锯齿形切屑形态
实验与模拟发现,随着切削速度的提高,切屑形态由低速时的带状切屑转变为锯齿形切屑。图3是切削速度为113.4 m/min,刀具前角为0°,切削厚度为0.10 mm时高温合金的切屑形态。图3(a)为实验所得切屑金相照片,图3(b)为模拟所得的切屑形貌图。高速切削过程中,第一变形区内的温度瞬间升高,造成材料的热软化效应超过了加工硬化效应,第一变形区处于绝热剪切失稳状态,剪切抗力迅速减小,材料的承载能力下降,切屑沿主剪切区发生周期性的绝热剪切断裂最终导致了锯齿形切屑的形成。图中实验所得的锯齿形切屑形态与模拟结果基本吻合,切屑2齿之间形成规则而狭窄的绝热剪切带,锯齿形状比较锋利,这证明了有限元模拟可以较为准确地预测高速切削过程中的切屑形态。

图3 模拟与实验切屑形态对比Fig.3 Comparison between simulated and experimental chip morphologies
2.2 瞬态切削力
图4为切削参数与图3相同时的瞬态切削力曲线图,其中图4(a)为实验测量的瞬态切削力曲线图,4(b)为模拟所得的瞬态切削力曲线图。
图4中,切削加工达到稳态时,切削力出现规律性波动,这与锯齿形切屑的形成有关。刀具对工件进行切削加工时,被切削材料会逐渐达到发生剪切断裂时的等效塑性应变,材料发生断裂,切屑与工件分离,切削力减小。随着刀具的继续切削加工,刀具与新的工件材料接触,切削力增大,当切削进行一段时间后,又会出现切屑与工件的分离,切削力又减小,如此往复地进行[8]。由图4可知,实验与模拟所得的切削力波动图非常接近。

图4 实验与模拟瞬态切削力对比Fig.4 Comparison between experimental and simulated transient cutting forces
2.3 Mises等效应力与应变
图5为切削条件与图3相同时,刀-屑接触面上某一个单元的Mises等效应力随着时间的变化曲线。

图5 米塞斯应力随时间变化曲线Fig.5 Curve of Mises stress vs time
由图5可知,初始Mises等效应力为0,随着切削进行,数值不断变大,当此单元及周围部分与刀具相互作用形成切屑时,则出现最大的Mises等效应力,刀具继续进行切削,此单元相应的Mises等效应力又逐渐减小。由此可知,随着切削的进行,切屑开始形成的部分会出现最大的应力值,向曲线两侧数值逐渐减小[5]。从曲线中还可以看到Mises等效应力出现波动,这与切削力达到稳定状态后出现波动的原因相似。切削参数与图3相同时,模拟的锯齿形切屑绝热剪切带内等效塑性应变分布的带状图、等高线云纹图及实验所得绝热剪切带的金相照片如图6所示。

图6 第一变形区应变分布的模拟及实验结果Fig.6 Simulated and experimental results of strain distribution in the primary deformation zone
从图6(a)中可以看出,该加工条件下绝热剪切带内发生很大的局部化变形,带内平均应变值在5左右。图6(b)中绝热剪切带内等效塑性应变等高线呈梯度变化,越靠近绝热剪切带中心,对应的等效塑性应变越大;距离绝热剪切带中心越远,对应的等效塑性应变越小。锯齿形切屑的各个剪切带之间材料发生的塑性应变极小,几乎为零。图6(c)可以看到,绝热剪切带内晶粒很小,说明由于剪切变形的高度局部化引起了绝热剪切带内晶粒细化。绝热剪切带周边区域的晶粒沿着剪切的方向被拉长。而远离剪切带区的晶粒变形很小,基本没有变化。对比研究表明,有限元模拟所得第一变形区的应变分布情况与实验基本一致,能够反映主剪切区应变的分布情况。
2.4 切削参数对锯齿形切屑形成过程的影响
2.4.1 切削参数对锯齿形切屑形态的影响
对于锯齿形切屑,常采用锯齿化程度GS[4]衡量锯齿形切屑的变形程度。GS的定义如下:
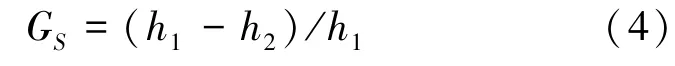
为了研究切削速度对于切屑形态的影响,实验与模拟采用相同的切削参数,即刀具前角为0°,切削厚度为0.10 mm,切削速度分别为45.4、70.6、113.4 m/min。此时,实验与模拟所得切屑的锯齿化程度的对比结果如图7所示。

图7 不同切削速度下实验与模拟锯齿化程度对比Fig.7 Comparison between experimentaland simulated sawtooth degree under different cutting speeds
由图7可知,模拟所得的切削速度对锯齿化程度的影响趋势与实验结果基本一致,能够预测切削速度对切屑锯齿化程度的影响,即随着切削速度的增大,锯齿化程度增大。这是因为随着切削速度的提高,工件材料的应变率变大,同时切削速度的增加也会引起切削热增加,而切削变形时间却大大缩短,切削热不能及时散出,使得热软化效应大于材料的硬化效应,造成绝热剪切变形加剧,从而更有利于锯齿形切屑的形成。
当切削速度为113.4 m/min,切削厚度为0.10 mm,刀具前角分别为-10°、0°、10°时,实验与模拟得到的切屑锯齿化程度的对比如图8所示。可以看出,实验和模拟结果都表明刀具前角对锯齿化程度的影响具有相同的规律,并且模拟结果与实验结果较为接近。随着刀具前角的增加,切屑锯齿化程度逐渐减小。这是由于刀具前角越小,刀具与切屑接触的摩擦区压应力就越大,同时,主剪切区内剪切应变加剧,造成切削热增加,温度升高,导致绝热剪切变形更明显,切屑变形程度更大。
切削速度为113.4 m/min,刀具前角为0°,切削厚度分别为0.07、0.10和0.15 mm时,实验与模拟所得的切屑锯齿化程度结果如图9所示。由图可知,模拟结果与实验结果趋势一致,都是随着切削厚度的不断增加,锯齿化程度不断增大。切削厚度越大,切削加工时产生的热量就越多且热量不容易扩散,绝热剪切热软化作用更加明显,导致锯齿形程度加剧。

图8 不同刀具前角下实验与模拟锯齿化程度对比Fig.8 Comparison between experimental and simulated sawtooth degree under different tool rake angles

图9 不同切削厚度下实验与模拟锯齿化程度对比Fig.9 Comparison between experimental and simulated sawtooth degree under different cutting thickness
2.4.2 切削参数对切削力的影响
为了研究不同切削速度对切削力的影响规律,实验和模拟采用与图7相同的切削参数。将实验和模拟获得的稳态切削时的平均主切削力进行对比,如图10示。

图10 不同切削速度下实验与模拟平均主切削力对比Fig.10 Comparison between experimental and simulated average principal cutting force under different cutting speeds
由图10可知,模拟结果与实验结果基本吻合,变化趋势都是随着切削速度的提高,平均主切削力降低,这说明切削速度对切削加工过程中的切削力具有重要的影响。随着切削速度的增加,高速切削过程中高温合金材料的变形速率增大,导致变形区内温度大幅升高,材料软化作用增强而硬化作用减弱,当达到绝热剪切条件后,材料内部出现绝热滑移,切削力减小。
图11为与图8所述切削条件相同时,实验与模拟所得稳态切削时平均主切削力的对比情况。由图可知,模拟所得平均主切削力随刀具前角的变化趋势与实验所得的情况一致。刀具前角越小,平均主切削力越大。这是因为刀具前角越小,相应的剪切角就变小,剪切应力越大,刀-屑接触面上的正应力增大导致摩擦力变大,致使切削力增大。

图11 不同刀具前角下实验与模拟平均主切削力对比Fig.11 Comparison between experimental and simulated average principal cutting force under different tool rake angles
图12为切削参数与图9相同时,实验与模拟获得的稳态切削时平均主切削力的对比情况。可以看出,模拟结果与实验结果具有较好的一致性,变化趋势都是平均主切削力随着切削厚度的增加呈上升趋势。切削力增大的主要原因是因为随着切削厚度的增加,单位时间内刀具的切削面积变大,相应的切屑的变形抗力增加,同时导致前刀面承受的正压力升高,产生的摩擦抗力增大,从而导致切削力大幅提高。

图12 不同切削厚度下实验与模拟平均主切削力对比Fig.12 Comparison between experimental and simulated average principal cutting force under different cutting thickness
2.4.3 切削参数对等效塑性应变的影响
在实验和模拟所得的锯齿形切屑上都发现了明显的绝热剪切带,如图3所示。切屑的锯齿化程度与绝热剪切带内发生的剪切应变有着密切关系。当一个完整的锯齿形切屑形成之后,绝热剪切带内的剪切应变计算公式如下[12]:

式中:L为锯齿间距,H为切屑的高度,h为锯齿的高度,ac为切削厚度,δ为绝热剪切带的平均宽度,γ0为刀具前角,v为切削速度。
根据式(5),测量出相应的参数就可以计算锯齿形切屑绝热剪切带内的剪应变。由模拟结果可以得出锯齿形切屑绝热剪切带内的平均等效塑性应变,模拟数据与实验计算出的值进行对比,如图13所示。
图13表明,模拟结果与实验结果趋势一致,随着刀具前角的增大,对应的锯齿形切屑绝热剪切带内的等效塑性应变减小。这说明刀具前角对锯齿形切屑绝热剪切带内的等效塑性应变有重要影响,刀具前角越小,刀具与切屑之间的接触长度越大,刀具对切屑的挤压作用增大,从而被加工材料受到刀具的切削作用形成锯齿形切屑时,绝热剪切带内发生的剪切滑移变形加剧,导致等效塑性应变增大。
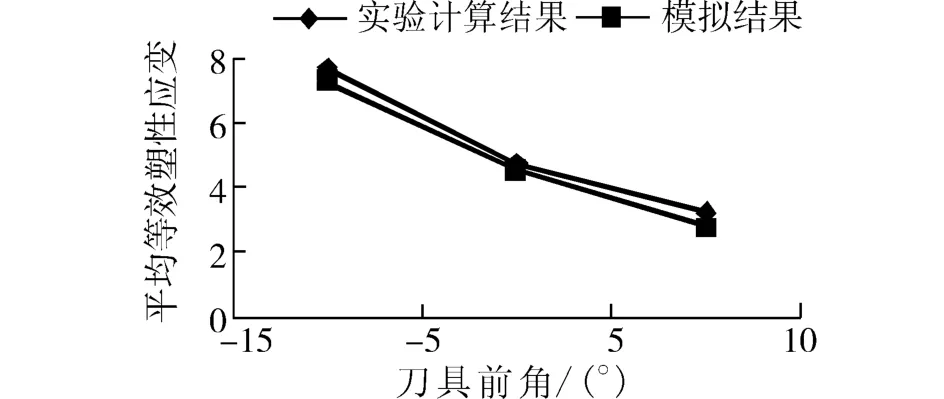
图13 不同刀具前角下实验与模拟平均等效塑性应变对比Fig.13 Comparison between experimental and simulated equivalent plastic strain under different tool rake angles
3 结束语
使用ABAQUS建立了高速切削高温合金的有限元模型,采用Johnson-Cook热粘塑性材料本构模型、剪切损伤切屑分离准则以及刀-屑界面粘结-滑移混合摩擦模型,对高速切削高温合金过程中的切屑形态及切削力进行了研究。研究结果表明,锯齿形切屑的锯齿化程度随着刀具前角的增加而减少,同时随着切削速度的增加及切削厚度的增加而增大。切削力随着切削速度和刀具前角的增大而减小,随着切削厚度的减小而减小。不同的刀具前角会影响锯齿形切屑绝热剪切带的形成,刀具前角越小,绝热剪切带内等效塑性应变越大。通过模拟与实验结果的对比研究表明,两者有较好的一致性,说明本文提出的有限元模型能够用来较为准确地预测高速切削过程中锯齿形切屑的形成和切削力。
[1]SHAW M C,VYAS A.The mechanism of chip formation with hard turning steel[J].CIRP Annals-Manufacturing Technology,1998,47(1):77-82.
[2]KOMANDURI R,BROWN R.On the mechanics of chip segmentation in machining[J].Journal of Engineering for Industry,1981,103:33-51.
[3]ODESHI A G.Effect of heat treatment on adiabatic shear bands in a high-strength low alloy steel[J].Materials Science and Engineering,2006,419:69-75.
[4]SCHULZ H,ABELE E,SAHM A.Material aspects of chip formation in HSC machining[J].CIRP Annals-Manufacturing Technology,2001,50(1):45-48.
[5]孔虎星,郭拉凤,尹晓霞.基于ABAQUS的钛合金切削有限元分析[J].机电技术,2011(4):22-23.
KONG Huxing,GUO Lafeng,YIN Xiaoxia.FE simulation of titanium alloy cutting based on ABAQUS[J].Mechanical and Electrical Technology,2011(4):22-23.
[6]VAZIRI M R,SALIMI M,MASHAYEKHI M.A new calibration method for ductile fracture models as chip separation criteria in machining[J].Simulation Modelling Practice and Theory,2010(18):1286-1296.
[7]UMBRELLO D.Finite element simulation of conventional and high speed machining of Ti6Al4V alloy[J].Journal of Material Processing Technology,2008,196:79-87.
[8]蒋志涛,刘泓滨,王飞,等.ABAQUS的高速铣削二维仿真分析[J].现代制造工程,2008(8):45-47.
JIANG Zhitao,LIU Hongbin,WANG Fei,et al.Finite element analysis of two-dimensional high-speed milling process based on ABAQUS[J].Modern Manufacturing Engineering,2008(8):45-47.
[9]王威.高速切削加工高温镍基合金GH4169的切削力和切削热的研究[D].青岛:青岛理工大学,2010:53.
WANG Wei.High-speed machining high temperature alloy GH4169 nickel-based cutting force and cutting heat[D].Qingdao:Qingdao University of Technology,2010:53.
[10]ZOREV N N.Inter-relationship between shear process occurring along tool face and shear plane in metal cutting[C]//International Production Engineering Research Conference.New York,USA,1963:42-49.
[11]ZHANG B,BAGCHI A.Finite element simulation of chip formation and comparison with machining experiment[J].Journal of Engineering for Industry,1994,116:289-297.
[12]DUAN C Z,WANG M J,PANG J Z.A calculational model ofshear strain and strain rate within shear band in a serrated chip formed during high speed machining[J].Journal of Materials Processing Technology,2006,178:274-277.
Finite element simulation of the formation process of a serrated chip in high-speed cutting
DUAN Chunzheng,WANG Zhaoxi,LI Honghua
(Key Laboratory for Precision and Non-Conventional Machining of the Ministry of Education,Dalian University of Technology,Dalian 116024,China)
In order to study and predict the formation process of the serrated chip in high-speed cutting(HSC),a finite elementmodelofthe high-speed cutting ofsuperalloy was constructed by using the finite elementanalysis software ABAQUS.By the adoption ofthe Johnson-Cook thermalvisco-plastic constitutive model,the separation criterion of the chip damaged in shearing and the sticking-sliding mixed friction model of the tool-chip interface,as well as the morphology ofthe serrated chip and the cutting force in the high-speed cutting of the superalloy were studied.Through the contrast analysis of the simulation and experiment,the results verify the accuracy of the finite element model.The research results of the effects of the cutting parameters on the chip show that the serrated degree of the chip formed in the high-speed cutting,the cutting force and the equivalent plastic strain inside the adiabatic shear band regularly change with the variation of the cutting speed,rake angle of the cutter and cutting thickness.
high-speed cutting;finite element simulation;serrated chip;superalloy;constitutive model;chip separation criterion
10.3969/j.issn.1006-7043.201212074
TG506
A
1006-7043(2014)02-0226-07
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201212074.html
2012-12-18.网络出版时间:2014-1-2 14:55:22.
国家自然科学基金资助项目(50875033).
段春争(1970-),男,副教授,博士.
段春争,E-mail:duancz@dlut.edu.cn.

