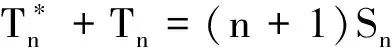两两PQD序列部分和之和的一个大数律

沈建伟

(浙江科技学院理学院,浙江 杭州 310023)

0 引 言

Resnick[1]及Arnold等[2]在研究纪录值的极限理论时发现有对随机变量序列部分和之和的极限性质进行研究的必要性.事实上,随机游动、破产理论及时间序列理论中均有必要研究部分和之和.文献[3-4]得到了I.I.D.随机变量序列部分和之和的强大数定律;文献[5-6]得到了对称同分布NA序列随机变量部分和之和的大数定律;文献[7-8]研究了对称分布的两两NQD序列随机变量部分和之和的强大数定律;文献[9]推广了文献[10]的结论,得到了分布对称但不同分布的PA序列部分和之和的弱大数定律,并通过对PA列收敛速度的限制弱化了文献[10]中定理的条件.本文把结果推广到了两两PQD序列随机变量部分和之和的情形,并去除了分布对称和同分布的限制条件.

定义1[11]称随机变量X和Y是PQD(positively quadrant dependent)的，若对∀x,y∈R都有

P{X≤x,Y≤y}≥P{X≤x}P{Y≤y}.

称随机变量序列{Xn,n≥1}是两两PQD的，若对∀i≠j,Xi与Xj是PQD的.

定义2若随机变量X与-X同分布,则称X为对称随机变量.

引理1[11]设随机变量X和Y是PQD的，则

1)EXY≥EXEY;

2) 若f,g同为非降(或非增)函数，则f(X)与g(Y)仍为PQD的.

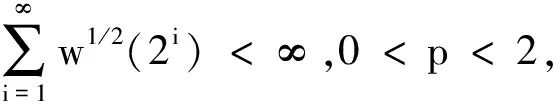
引理4[13]设{Xn,n≥1}是任意随机序列.如果存在某随机变量X,使对任意x>0及n≥1,有P{|Xn|≥x}≤cP{|X|≥x},则对∀β>0,∀t>0有

E|Xn|βI(|Xn|≤t)≤c(E|X|βI(|X|≤t)+tβP{|X|>t}),E|Xn|βI(|Xn|>t)≤cE|X|βI(|X|>t).

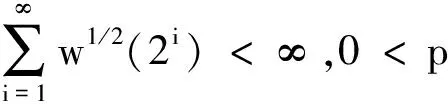
1 主要结果

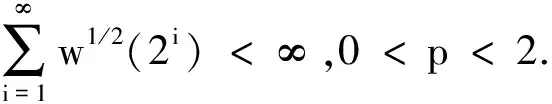
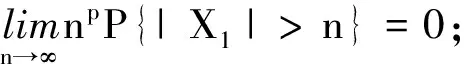
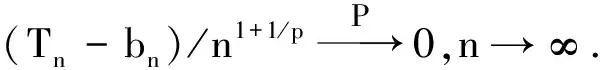
2 定理的证明

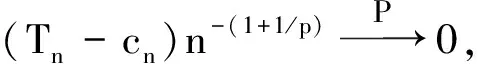
又因为两两PQD序列的对称化序列仍是两两PQD序列，故只需对对称化序列证明定理成立即可.

首先，考虑满足条件(A)的情形：

不失一般性,不妨设{Xi,i≥1}为分布对称的同分布两两PQD序列,且设bk=0,k≥1;首先证明:对∀ε>0,有

(1)

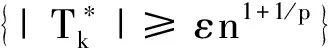
(2)

(3)

由式(3),{Xi,i≥1}的同分布性可知

(4)

对∀β>0,由式(3)可知,存在N0>0,当k>N0时,有

(k+1)P(|X1|>k1/p)<β/8.

(5)

由Markov不等式,引理2,{Xi,i≥1}的同分布性可得

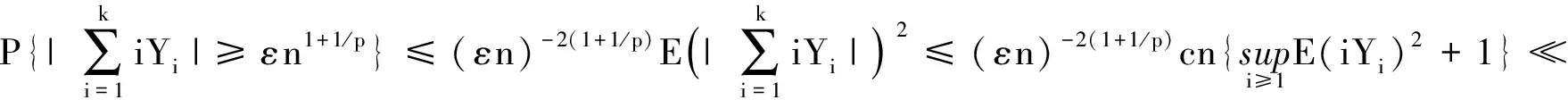
n1-2/p{E|Y1|2+1}≤nP{|X1|>n1/p}+n1-2/pE|X1|2I(|X1|≤n1/p)+n1-2/p

(6)

:=I21+I22+I23.

对于I21=nP{|X1|>n1/p},对于充分大的n,利用式(3)可得

I21<β/4.

(7)

对于I23=n1-2/p,由0

I23<β/4.

(8)

对于充分大的n,利用式(5)、(8)可得

(9)

(10)

其次，考虑满足条件(B)的情形：

(11)

由Markov不等式,引理2,引理4可得

nP{|X|>n1/p}+n1-2/pE|X|2I(|X|≤n1/p)+n1-2/p:=I21+I22+I23.

定理1得证.

[1]Resnick S I. Limit laws for record values[J].Stochastic Processes and their Applications,1973,1(1):67-82.

[2]Arnold B C, Villasenor J A. The asymptotic distributions of sums of records[J].Kluwer Academic Publishers,1998,1(3):351-363.

[3]江涛,林日其.I.I.D.随机变量部分和之和的极限定理[J].淮南工业学院学报,2002,22(2):73-78.

[4]江涛,苏淳,唐启鹤.I.I.D.随机变量部分和之随机和的极限定理[J].中国科技大学学报,2001,31(4):394-399.

[5]宇世航.同分布NA序列部分和之和的弱大数定律[J].哈尔滨师范大学学报：自然科学版,2004,20(4):39-42.

[6]宇世航.同分布NA序列部分和之和的强大数定律[J].山东大学学报：理学版,2008,43(4):62-66.

[7]兰冲锋,吴群英,叶大相.同分布两两NQD序列部分和之和的强大数定律[J].桂林理工大学学报,2010,30(4):640-643．

[8]俞周晓,王文胜.不同分布两两NQD列部分和之和的强大数定律[J].杭州师范大学学报：自然科学版,2012,11(5):436-442.

[9]俞周晓,王文胜.PA序列部分和之和的弱大数定律[J].杭州师范大学学报：自然科学版,2012,11(2):181-184.

[10]查婷婷.同分布PA序列部分和之和的弱大数定律[J].安徽建筑工业学院学报：自然科学版,2009,17(4):94-96.

[11]Lehmann E L. Some concepts of dependence[J].The Annals of Mathematical Statistics,1966,37(5):1137-1153.

[12]刘庆.两两PQD序列的大数定律[J].浙江大学学报：理学版,2011,38(2):140-143.

[13]吴群英.混合序列的概率极限理论[M].北京:科学出版社,2006.