基于Kurtosis-IHS的遥感影像融合

，，，

(北京师范大学信息科学与技术学院，北京 100875)

0 引 言

随着计算机技术、航空航天技术以及遥感技术的飞速发展，遥感影像向着高光谱、高分辨率、多时相(多源)方向发展，它们以不同的空间尺度、不同的时间周期、不同的光谱范围以及不同的扫描方式和极化方式，多方面地反映地物目标的各种特性，构成同一区域的多源数据(王爱玲等，2006)。然而，由于技术条件和工作原理的不同，任何来自单一传感器的信息都只能反映目标的某一个或几个方面的特征，而不能反映出全部特征，存在信息量不足的问题。与单源信息相比，多源数据存在互补性和冗余性，必须针对性地消除冗余，以减少数据处理量，同时，必须对多源数据进行融合处理，以充分发挥各传感器数据的优势，提取更丰富、更可靠、更有用的信息。影像融合已经在自动目标识别、遥感、医学图像处理等领域有着广泛的应用(Ashraf et al, 2012； Sapkal et al, 2012; Zhang et al, 2012)。

多光谱遥感图像不同波段的融合，由于所融合的波段的不同或者波段数量的差异，信息量会出现不同程度的缺失或过量，会导致融合图像欠饱和或过饱和的现象(Kotwal et al, 2013)。多光谱成像传感器充分利用地物在不同光谱区的反射特征可获得多个光谱波段的遥感图像，但其成像分辨率较低，清晰度差。而全色成像传感器可获得高空间分辨率的全色波段遥感图像，但其光谱分辨率较低。如何综合利用多光谱遥感图像与全色波段遥感图像各自的信息优势，有效地对不同波段的信息融合，获得具有高空间分辨率和高光谱分辨率的融合图像是当前遥感影像数据处理领域中的研究热点(Pohl et al, 1998)。

目前常用的多光谱影像与全色影像融合方法包括：IHS变换(IHS)(Carper et al, 1990)、Brovey变换(Pohl et al, 1998)、主成分变换(PCA)(pohl et al, 1998)、离散小波变换(DWT)(Li et al, 1995)、曲波变换(Curvelet)(张强等，2007; Choi et al, 2005)、非负下采样变换(NSCT)(杨粤涛等，2011)以及独立成分分析方法(ICA)(Yu et al, 2012)等。其中IHS融合方法因其简单、快速的优点而得到广泛应用。IHS方法可以有效地提高融合影像的空间分辨率，同时由于IHS方法使用全色图像替换分量，未能均衡地使用全色图像信息以及多光谱图像信息，容易造成所引入的全色图像信息过量以及多光谱图像信息不足的问题，在视觉上的表现就是所获得的融合图像会有不同程度的光谱畸变，并且会引入全色图像所包含的噪声，在很大程度上降低了融合质量(Tu et al, 2001; Wang et al, 2005)。

峭度(Kurtosis)是用来描述某变量所有取值分布形态陡缓程度的统计量，因其在统计意义上是一个随机变量的非高斯性度量而被广泛用于特征提取(余先川等，2001；Sachdeva et al, 2013)。现实中的噪声往往呈现正态分布即高斯分布，乔建苹(2011)证实从统计学角度分析得到的峭度图像具有高斯不变性，峭度图像不易受到噪声的影响，并提出在低信噪比的环境下使用峭度图像来对影像进行特征提取。

为此，提出了一种基于Kurtosis-IHS遥感影像融合方法：首先分析了传统IHS方法光谱失真的本质原因，使用光谱图像融合系数逼近的方法以减少光谱失真；同时为克服传统的IHS方法易引入噪声的问题，提出使用峭度的方法来解决该问题。这种融合方法克服了传统的IHS方法光谱失真过大以及易引入噪声的问题。

1 Kurtosis-IHS遥感影像融合

1.1 传统IHS遥感影像融合方法的缺点

传统的IHS遥感影像融合方法首先将多光谱图像从原始空间变换到IHS空间，以获得强度(Intensity，即I分量)、色度(Hue，即H分量)、饱和度(Saturation，即S分量)3个分量；然后将高空间分辨率的全色图像进行线性拉伸，使得拉伸后图像的均值和方差与 IHS空间中的I分量一致，以达到直方图匹配；最后，将拉伸后的影像作为新的强度分量，与H分量和S分量一起利用 IHS逆变换回原始空间。

对于波段数为N的多光谱影像，I分量的计算公式为：

(1)

式(1)中Mi表示第i个波段的多光谱图像。

直方图匹配公式为：

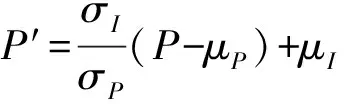
(2)

式(2)中,σP和σI、μP和μI分别表示全色图像以及I分量的方差及均值大小。

因此,融合后各个波段融合图像Fi可以用公式表示为:

Fi=Mi+(P′-I)

(3)

由式(3)可以知道,当公式中的第二项(P′-I)值越小时,融合后各波段图像Fi则更加逼近相应的多光谱图像Mi;反之则光谱失真越大。因此,可以推出造成光谱扭曲的本质原因是全色图像P分量与I分量差异过大,直接进行分量替换会引入过量全色图像信息,造成全色图像信息冗余以及多光谱图像信息不足。

另一方面，传统的IHS融合方法使用全色图像P分量对I分量进行替换，能够有效地提高融合图像的空间分辨率，但是没有考虑到全色影像包含噪声干扰时对融合结果所造成的影响。当使用带噪声的全色图像对I分量进行替换，则会将噪声等干扰加入到融合影像之中，因此会对融合质量产生较大的影响。

1.2 峭度及峭度图像

峭度是随机变量的四阶累积量，用来描述某变量所有取值分布形态陡缓程度的统计量，是对随机变量的非高斯性度量。通常利用峭度进行信息提取，一般情况下峭度值越大，所含有的目标信息就越多，噪声干扰越小。

对于一个零均值的随机变量s，其峭度定义为：

kurt(s)=E{s4}-3{E{s2}}2

(4)

其中E{·}表示变量的数学期望。

对于一幅影像g,其相对应的峭度图像kurtg的计算方法如下(乔建萍，2011):首先计算图像g中某一像素g(n1,n2)的局部峭度值,对于峭度局部窗口大小为(2k+1)×(2l+1),像素g(n1,n2)对应的峭度值kurtg(n1,n2)的计算公式如式(5)所示;对于图像的边缘点,采用循环边界法对图像进行周期延拓,并按照公式(5)计算相应的峭度值;最后对整个图像进行遍历,得到图像g对应的峭度图像kurtg。

(5)

实验中,峭度局部窗口取3×3像素大小。

1.3 基于Kurtosis-IHS的遥感影像融合

由公式(3)可知，若P分量逼近I分量，即(P′-I)值越小，则融合后的F图像越逼近多光谱图像，即当

(6)

成立，则光谱扭曲最小，光谱保真度越高。因此，公式(6)转变为求解多光谱图像融合系数αi的最优逼近解。

根据公式(6)中的逼近公式以及约束条件，构造无约束的目标函数，通过最小化目标函数来估计多光谱图像融合系数α1,α2,…，αN的解，最小化目标函数如式(7)所示：

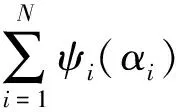
(7)

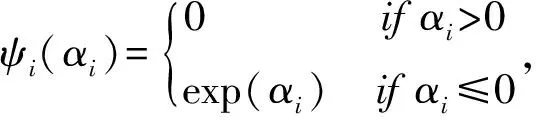
ψi(αi)=(αi≤0)·exp(αi)

(8)

使用梯度下降法求解目标函数，得到多光谱各波段融合系数α1,α2,…αN的迭代解，其迭代公式如式(9)所示：

(9)

其中,τ为迭代步长。

另一方面，公式(3)的第二项表示的是细节信息即空间信息的增加。考虑到噪声的影响，在公式的第二项上增加了一个系数，即当噪声越大，系数越小，取值范围为0～1。则得到基于Kurtosis-IHS 的融合公式：

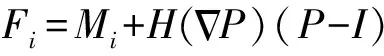
(10)

1.4 基于Kurtosis-IHS影像融合步骤

基于Kurtosis-IHS的影像融合方法其计算过程分为三部分：使用梯度下降法根据迭代公式进行迭代计算多光谱各波段图像系数αi；由全色图像获取峭度图像，并计算得到相应的归一化映射图像。根据融合公式获得各波段融合图像。融合过程如下。

基于Kurtosis-IHS影像融合方法:

输入:全色图像P,以及多光谱各波段图像M1,M2,…,MN

输出:融合后的各波段图像F1,F2,…,FN

步骤：

(1) 计算多光谱各波段图像系数α1,α2,…,αN。

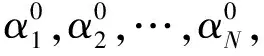
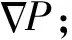
(3) 根据Kurtosis-IHS融合公式得到融合图像。

2 实验结果及评价

为了验证本算法的有效性，实验选取了2组遥感影像进行融合：第1组(图1 a—b)所采用的数据源是中巴地球资源一号卫星(CBERS)影像和Landsat ETM+影像，实验区位于广东省珠海市斗门区，其中多光谱图像显示是由B3、B2、B1 3个波段合成的假彩色图像；第2组实验数据(图1 a—b)来自德国TerraSAR-X卫星于2008年获取的珠三角地区的空间分辨率为1 m的雷达影像以及SPOT 5号卫星拍摄的相应地区的分辨率为10 m的多光谱影像，其中多光谱影像显示是由B3、B2、B1 3个波段合成。2组实验数据均为已配准好的遥感影像，影像大小为512×512像素。

2.1 融合结果及评价

为了更加客观地对比试验方法，将本研究所提出的方法分别与IHS、PCA、DWT、NSCT方法对2组数据进行融合对比实验，融合结果如图1 c—g以及图2 c—g所示。

首先，采用目视解译的方法对几种方法的融合结果进行定性评价。从图1和图2可以看到，2组图像中这5种方法均将高分辨率影像的空间信息以及多光谱影像的光谱信息有效地进行了结合，融合影像在分辨性以及清晰性上得到了提高。但是，基于IHS、PCA、DWT、NSCT几种融合方法光谱均有不同程度的扭曲，而本研究所提出的算法光谱保持较好。本研究融合方法所得到的融合图像整体视觉效果更加接近原始的多光谱图像，图1 b—f中的山体区域(黄色框圈示)颜色扭曲较大，而图1g中的山体区域颜色保持得比较好；仔细对比图2中的居民区域(黄色框圈示)，可以看到IHS以及PCA方法在该融合区域出现颜色过饱和的现象，而DWT以及NSCT方法在该区域则表现出多光谱信息不足；在图2的水体区域(红色框圈示)，同样地可以看到本研究算法融合结果光谱失真较小。

图1 第一组遥感影像融合实验

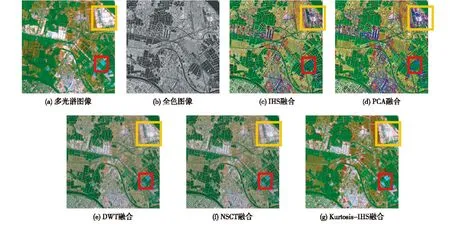
图2 第二组遥感影像融合实验

为更加有效地对遥感影像融合结果进行评价，本研究使用5项质量评价指标来客观评价光谱失真程度，即相关系数(CC)、相对整体维数综合误差(ERGAS)、相对平均光谱误差(RASE)、均方根误差(RMSE)、光谱信息散度(SID)(余先川等，2012; Chang, 1999; Choi et al, 2005)。这5组评价指标数值越小，表明光谱保持越好，即光谱失真越少，融合效果越好。

表1及表2分别对应这2组遥感影像不同融合方法下的融合结果各质量评价指标值。对比表1中的各质量评价指标，本研究算法的CC、ERGAS、RASE、RMSE这4项指标均达到最小，即光谱保持最好，SID指标质量处于第二；将本研究算法与IHS方法相比，5项质量评价指标均好于IHS方法，CC、ERGAS、RASE、RMSE及SID分别较IHS方法提高了89.15%、1.61%、1.94%、1.94%、8.49%。同时，从表2中可以看到，本研究算法各项评价指标均达到了最小，即光谱失真最小，融合效果最好，与IHS方法相比，CC、ERGAS、RASE、RMSE以及SID分别提高了41.80%、57.09%、57.11%、57.11%、49.74%。表1及表2的质量评价指标表明，基于Kurtosis-IHS的方法克服了光谱严重失真的问题，光谱扭曲小。

表1 第一组遥感影像融合结果质量评价

表2 第二组遥感影像融合结果质量评价

2.2 抗噪效果评价

为了验证本研究所提出的算法在抑制噪声方面的有效性，对图1及图2的2组遥感数据分别加入不同功率的噪声，并使用峰值信噪比(PSNR)来对含噪环境下的融合结果进行质量评价。其中，PSNR值越大，表明抗噪性能越好。对2组全色影像分别添加零均值、方差大小分别为0.001、0.002、0.005的噪声，并使用IHS、PCA、DWT、NSCT以及本研究算法对含噪数据进行融合实验。

其中，图3 a—b、图3 c—d所示分别为2组遥感影像添加方差为0.005大小的噪声时IHS方法以及本研究方法的融合结果。从2组融合图像上看，传统的IHS融合图像噪声明显，而本研究融合方法融合图像在保持较好的融合效果时噪声得到了有效抑制。

表3、表4分别为2组遥感影像不同噪声功率下融合的PSNR值。从表3及表4可以看到，本研究算法各组不同噪声的融合图像PSNR值均达到最大，说明抗噪效果均达到最好。其中第一组遥感影像噪声方差分别为0.001、0.002、0.005时本研究算法相对于IHS融合方法PSNR值分别提高了1.02%、0.97%、0.78%，而对于第二组影像PSNR值则分别提高了64.18%、64.13%、64.15%，有效说明了所提出的算法在抑制噪声方面有较好的效果。

图3 噪声方差为0.005时2组影像IHS融合以及Kurtosis-IHS融合结果

表3 第一组遥感影像零均值不同方差噪声功率下融合的PSNR值

表4 第二组遥感影像零均值不同方差噪声功率下融合的PSNR值

3 结 论

IHS融合方法因其计算公式简单并且计算快速的优点而被广泛使用；同时峭度因其能度量随机变量的非高斯性度量而大量被用于特征提取。

研究针对传统的IHS方法由于全色图像信息量过大而造成光谱失真及所引入噪声的问题，使用了光谱图像融合系数逼近的方法，并提出使用基于Kurtosis-IHS的遥感影像融合方法。实验选取了2组多光谱图像与全色图像遥感影像数据进行对比实验，分别进行了不加噪声的实验以及加入不同功率大小噪声的融合实验。其中，不加噪声的融合实验结果表明，笔者所提出的算法较传统的IHS、PCA、DWT以及NSCT方法光谱扭曲小。同时，相对于传统的IHS方法，在CC、ERGAS、RASE、RMSE以及SID这5组质量评价上，第一组实验数据融合结果分别提高了89.15%、1.61%、1.94%、1.94%、8.49%，而第二组实验数据融合结果则在这5组评价指标上分别提高了41.80%、57.09%、57.11%、57.11%、49.74%。

含噪环境下的融合实验表明，笔者所提出的方法抗噪效果明显，与传统的IHS方法进行比较，加入不同方差大小分别为0.001、0.002、0.005的噪声时，在评价指标PSNR值上，第一组实验数据融合结果分别提高了1.02%、0.97%、0.78%，而第二组实验数据实验结果其PSNR值则分别提高了64.18%、64.13%、64.15%。实验结果充分表明了本研究所提出的Kurtosis-IHS方法优于传统的IHS融合方法，在保持较高空间分辨率的同时，克服了传统IHS融合方法光谱扭曲度大以及易引入噪声的问题。

乔建苹.2011. 基于峭度图像的超分辨率重建算法[J].计算机工程, 37(24)：200-203.

王爱玲, 李京, 刘素红, 等. 2006. 多源遥感影像数据的尺度整合方法[J]. 遥感信息，(5)：40-42.

杨粤涛, 朱明, 贺柏根, 等. 2011. 采用改进投影梯度非负矩阵分解和非采样Contourlet变换的图像融合方法[J]. 光学精密工程, 19(5)：1143-1150.

余先川, 胡丹. 2011. 盲源分离理论及应用[M]. 北京：科学出版社.

余先川, 裴文静. 2012. 针对不同融合算法的质量评价指标性能评估[J]. 红外与激光工程, 41(12)：3416-3422.

张强, 郭宝龙. 2007. 应用第二代Curvelet变换的遥感图像融合[J]. 光学精密工程，15(7)：1130-1136.

ASHRAF S, BRABYN L, HICKS B J. 2012. Image data fusion for the remote sensing of freshwater environments [J]. Applied Geography, 32(2)：619-628.

CARPER W, LILLESAND T, KIEFER R. 1990. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data [J]. Photogrammetric Engineering and Remote Sensing, 56(4)：459-467.

CHANG CHEINI. 1999. Spectral information divergence for hyperspectral image analysis[C]// IGARSS′99 Proceedings. Hamburg, Geman: IEEE, 1：509-511.

CHOI M, KIM R Y, NAM M R, et al. 2005. Fusion of multispectral and panchromatic satellite images using the curvelet transform [J]. Geoscience and Remote Sensing Letters, IEEE, 2(2)：136-140.

KOTWAL K, CHAUDHURI S. 2013. A novel approach to quantitative evaluation of hyperspectral image fusion techniques [J]. Information Fusion, 14(1)：5-18.

LI HUI, MANJUNATH B S, MITRA S K. 1995. Multisensor image fusion using the wavelet transform [J]. Graphical Models and Image Processing, 57(3)：235-245.

POHL C, VAN GENDEREN J L. 1998. Review article multisensor image fusion in remote sensing：concepts, methods and applications [J]. International Journal of Remote Sensing, 19(5)：823-854.

SAPKAL R J, KULKARNI S M. 2012. Image Fusion based on Wavelet Transform for Medical Application [J]. Image, 2(5)：624-627.

SACHDEVA J, KUMAR V, GUPTA I, et al. 2013. Segmentation, feature extraction and multiclass brain tumor classification [J]. Journal of Digital Imaging, 26(6):1141-1150.

TU TEMING, SU SHUNCHI, SHYU HSUENCHYUN, et al. 2001. A new look at IHS-like image fusion methods [J]. Information Fusion, 2(3)：177-186.

WANG ZHIJUN, ZIOU D, ARMENAKIS C, et al. 2005. A comparative analysis of image fusion methods [J]. IEEE Transactions on Geoscience and Remote Sensing, 43(6)：1391-1402.

YU XIANCHUAN, CAO HENZHI. 2012. Remote sensing image fusion based on integer wavelet transformation and ordered nonnegative independent component analysis [J]. GIS-cience & Remote Sensing, 49(3)：364-377.

ZHANG HAICHAO, ZHANG FANGFANG, SUN SHIBAO, et al. 2012. An Algorithm of Infrared and Visible Light Images Fusion Based on Infrared Object Extraction [M]//QIAN ZHIHONG, CAO LEI, SU WEILIAN, et al. Recent Advances in Computer Science and Information Engineering. Berlin, Gemany: Springer-Verlag Berlin and Heideberg GmbH & Co K, 2:159-165.