典型低矮双坡屋盖平均风压的数值模拟

， ，，

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

历次风灾调查表明[1]：我国东南沿海地区因台风而倒塌的低矮房屋超半数以上.双坡屋面建筑遭受台风侵害时，局部高负压导致的屋面破坏屡见不鲜[2].赵雅丽、黄鹏等[3]在B类和C类场地类别下对典型的低矮双坡建筑模型进行了风洞试验.认为30°坡角的迎风屋面表现为正压，背风面均为负压.风向角的影响也较大，除了局部屋面出现正压外其余部分均为负压区.王辉等[4]采用时均标准k—ε湍流模型对一低层双坡房屋的周围风场和表面风压进行了数值模拟.结果表明低层房屋的屋檐、屋脊和山墙顶边等交接部位出现较高的局部负压区.陈水福、吕少林[5]采用k—ε时均模型对屋面坡角和高宽比的影响进行研究，得到不同几何外形的屋面平均风压的分布曲线.迎风面风压绝对值随坡角增大而减小，背风面趋于增大，并推荐坡角为15°～30°；屋面风压与高宽比大小成正比.全涌、顾明等[6]对一系列低矮双坡屋盖进行研究，结论表明屋盖坡角的变化对最不利屋盖升力系数有重要影响：对高宽比相同的低矮建筑，屋面最大升力系数随屋盖坡角增大而减小.孙高勇、姚勇、李明[7]采用标准k—ε时均模型分析沿海地区底层双坡房屋.分析结果认为风向角影响较大，决定总体布局；屋面坡度建议范围为18°～34°；挑檐只有局部影响.笔者基于FLUENT分析软件，结合西尔斯结构实验楼实测数据，采用改进[8-10]的带旋流修正Realizablek—ε湍流模型，使用SIMPLEC分离算法，分析屋面倾角、挑檐长度和风向角等参数对低矮双坡屋面平均风压特性的影响.

1 数值模拟理论基础

低矮房屋的风荷载特性问题属于典型的钝体绕流问题，其数理模型的控制方程为不可压Navier-stokes方程，引入张量指标后方程可表示为

(1)

(2)

(3)

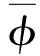
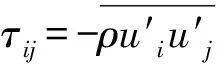
(4)

式中：ui为时均速度；k为湍动能；δij称“kronecker delta”求和约定.

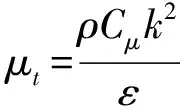
2 计算模型

西尔斯结构实验楼(SSB模型)是著名的低矮房屋实测模型，长宽高均为h=6 m，国内外学者对该模型做了大量的风洞试验和实测试验，获得了详细的实验数据[13].基于SSB模型的实测数据(图1)讨论典型低矮房屋(图2)的风压特性.

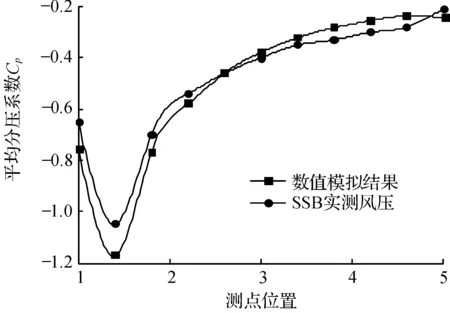
图1 SSB数值模拟结果与实测对比

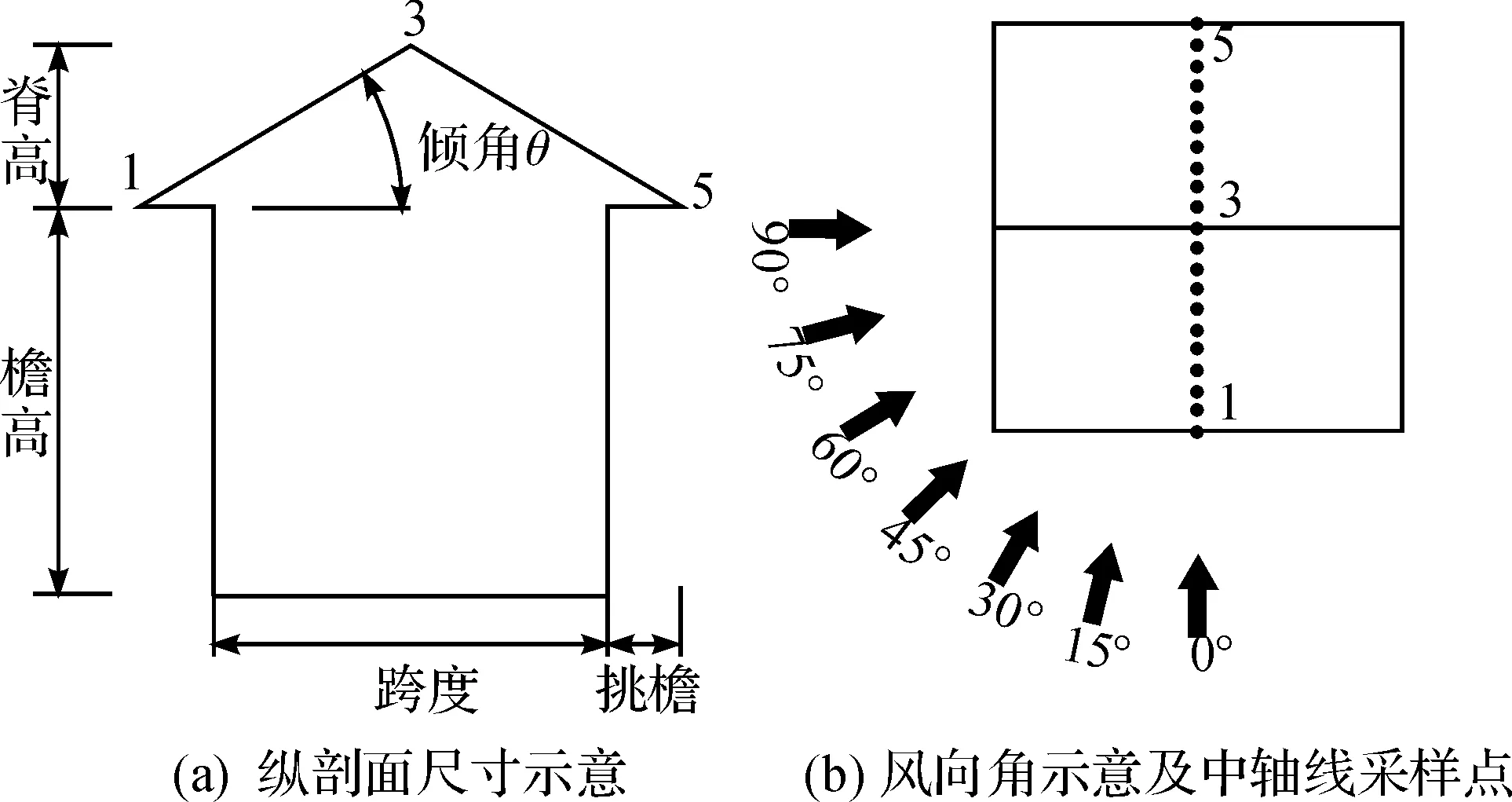
图2 尺寸示意、风向角及中轴线采样点

2.1 几何建模与网格划分

根据SSB模型尺寸建立足尺模型，檐高、跨度、长度均取h=6 m，几何尺寸如图2所示.计算域竖直方向为7h，长度为20h且将模型置于距入口三分之一长度处，流域宽度15h，流域尺寸满足阻塞率小于3%要求[14-15].

对建筑模型周围1.5h范围内的内流域进行适当加密，以满足近壁面流场运动特性.近壁面网格尺寸为0.15 m，内外流域过渡面网格尺寸为0.6 m，入流面最大网格尺寸为2 m，采用Delaunay 三角化法和推进阵面方法[16]划分四面体网格约120万，图3为整体流域与局部网格放大图.

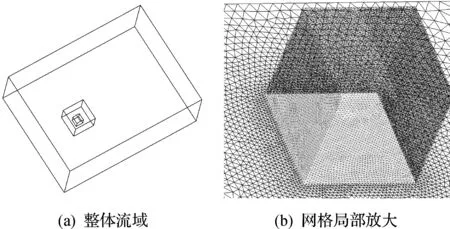
图3 非结构化网格示意图

2.2 边界条件及算法设置

流场速度入口(Velocity-inlet)入口采用自定义程序UDF进行对接；出流面选用压力出口(Pressure-outlet)；流域顶部及两侧采用对称边界(Symmetry)；建筑表面与流域地面为无滑移边界(Wall).配合非平衡壁面函数模拟钝体绕流的分离、再附等一系列复杂运动.根据SSB模型现场实测数据采用指数率模拟大气边界层风速剖面：

V(z)=Vb×(Z/Zb)α

(5)

式中：Vb=6.97 m/s；Zb=1 m；α=0.16.

湍流强度I(z)采用日本规范二类地貌的建议：

(6)

式中ZG=350 m.

计算中进流面据日本规范直接给定湍动能k和湍动耗散率ε与湍流积分尺度Lu的方程：

k(z)=1.5[I(z)×V(z)]2

(7)

(8)

(9)

式中Cμ=0.09.

模拟实验主要是稳态的分析，兼顾计算成本与精度的要求，选用Realizablek—ε湍流模型计算平均风压，采用二阶迎风离散格式，并选择分离式算法SIMPLEC完成对压力和速度的联合求解，迭代至收敛残差准则10-4且监测屋盖表面升力曲线直至稳定.

3 计算结果与分析

采用无量纲参数平均风压系数Cp和升力系数Cl作为屋盖风压特性的参考依据：

(10)

(11)

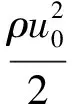
图1表明SSB实测数据与数值模拟结果(沿图2所示测点1-3-5)对比，认为风压分布趋势和精度与实测数据接近，可用于风压预测.

3.1 屋倾角与风向角影响分析

定义屋倾角正切值tanθ为檐脊相对高差与屋盖投影跨度的比值，如以工况WQJ01为正切值为0.1，风向角为0°，挑檐长度为0 m.风向角工况以设置角度0°～90°以每15°为一个工况，屋倾角选用WQJ06，挑檐长度0 m.由图4可知:0°风向角下迎风屋盖负风压总体趋势随倾角增大而减小，背风屋盖负风压趋势当屋盖倾角正切值0～0.3范围内则呈现增大趋势，而当屋盖倾角正切值超过0.5时，背风屋盖的负压变化不大，趋于稳定.其主要原因如图5所示：迎风屋面随着屋倾角的增大分离点与再附点之间的区域逐渐减小直至不产生分离，因而局部负压绝对值呈减小趋势；对于背风屋面，屋脊结构使得原本处于再附点下游的区域再次出现流动分离，增大了屋脊下游区域的局部负压，导致了背风屋盖升力增大；而当屋倾角正切值超过0.3时，背风屋盖上方流场产生回流现象，风压特性由此回流稳定控制，因而升力系数变化不大.

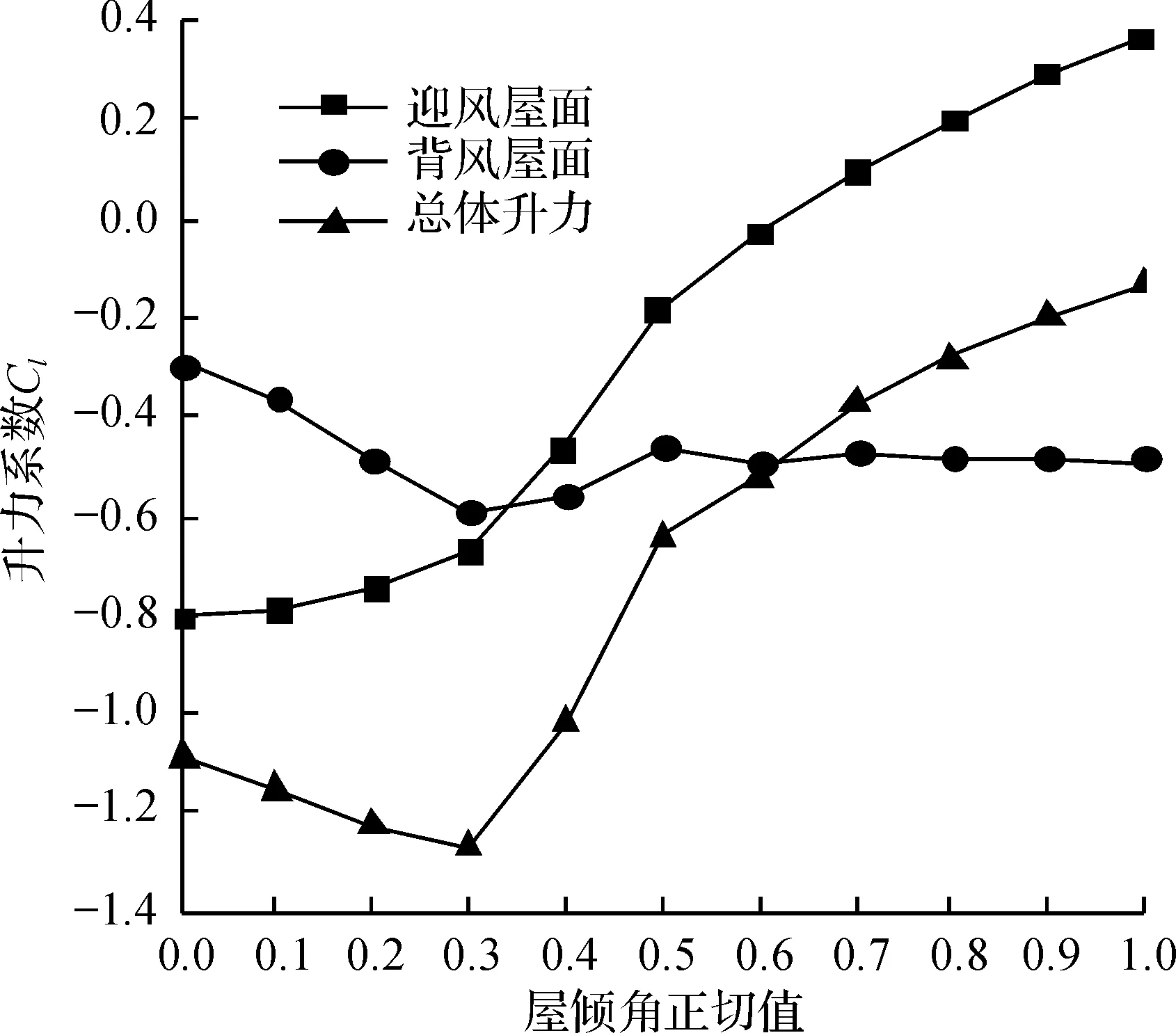
图4 屋盖倾角影响风压特性

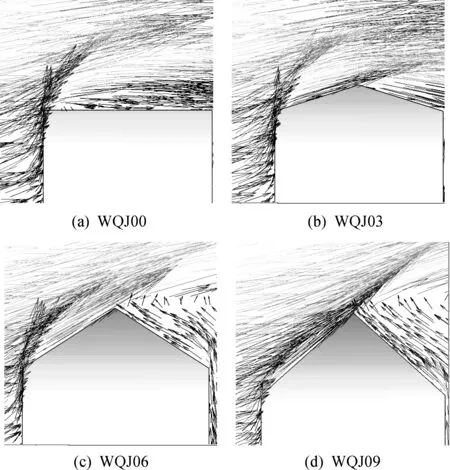
图5 各屋倾角工况下风速矢量图

由图6可知：当风向角在0°～30°度范围内时，迎风屋盖与背风屋盖变化趋势平缓；但是当风向角由30°开始增大时，迎风屋面的升力系数由正值向负值转化，且升力系数系数绝对值的变化梯度也越来越大，而背风屋面的升力系数依旧以负值为主，且在60°时升力系数绝对值达到最大，处于最不利风向角.

产生上述现象的原因可参考图7所示的四种风向角工况的风压系数云图进行解释：当风向角为0°～30°时，迎风面大部分处于0压力区，负压影响区域小，背风面则基本被-0.5所控制；当风向角达到60°时，迎风屋面均以负压为主，风压系数绝对值依旧保持增大趋势，背风面大部分被风压系数为-0.8～-1.0的区域所占据；当风向由60°继续向90°增大时，风压系数分级较多(-0.4～-1.8)，虽然迎风前缘的局部负压达到了-1.8，但低负压范围远超过该高负压区，局部高负压未起到决定作用.

图6 风向影响下屋盖升力系数

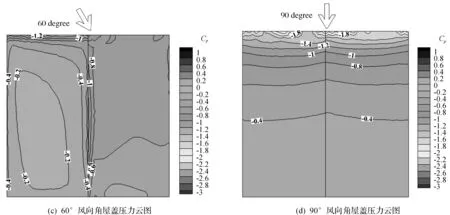
图7 0°，30°，60°，90°风向工况下压力云图

3.2 挑檐长度影响分析

模型采用屋倾角正切值为0.6，风向角0°，以TY05表示挑檐长度与檐高的比值为0.05，挑檐长度为0～1.8 m.

分析图8可得：倾角一定的双坡屋盖，挑檐长度对迎风屋面整体性影响与屋倾角相比作用不明显，但是挑檐可减小屋面前缘的分离作用(图9)，因此选取合适的挑檐长度可改变迎风屋面的负压情况；背风屋面受挑檐长度影响不大，挑檐长度改变60%的情况下升力系数仅改变13%，其主要原因为背风屋面受下游流场的漩涡情况影响程度有限，背风屋面屋檐处对流场分离的加剧作用不明显.

图8 不同挑檐长度升力系数对比

图9 TY00与TY20速度矢量图

4 结 论

结合SSB实测数据，采用FLUENT软件对低矮房屋屋盖平均风压特性进行了数值模拟证明了数值模拟预测建筑屋盖平均风压特性是可行的.在此基础上系统研究了低矮房屋在屋倾角、风向角、挑檐长度对屋盖风压分布的影响情况，得出以下结论：屋盖倾角对屋盖风压分布影响较大，迎风屋面随倾角增大而呈现由负压转至正压的趋势，屋倾角正切值超过0.6(约30°)时以正压为主.背风屋面始终以负压为主，且在倾角正切值为0.3(约18°)时达到最大值，超过0.6(约30°)时负压趋于稳定，变化平缓；风向角影响程度大，应最大程度地保持建筑旋转角度在15°范围内，避免置于60°的工况之下；合适的挑檐长度可减小迎风屋面局部的负压分布范围，从而最大程度地降低负压影响.

参考文献：

[1] 潘赛军.浙江台州工业厂房0414号台风受损的原因剖析与对策探讨[J].钢结构，2005，20(6)：52-57.

[2] 王凌.近35年登陆我国台风的年际变化特征及灾害特点[J].科技导报，2006，24(11)：23-25.

[3] 赵雅丽，黄鹏，全涌，等.典型双坡低矮建筑屋面风压分布特性试验研究[C]//第十三届全国结构风工程学术会议论文集.大连:中国学术期刊电子杂志社，2007.

[4] 王辉，陈水福，唐锦春.低层双坡屋面房屋表面风压的数值模拟[J].浙江大学学报：工学版，2003，37(6)：634-638.

[5] 陈水福，吕少林.低层双坡房屋屋面风荷载的数值研究——坡角和高宽比影响的分析[J].浙江大学学报：工学版，2006，40(10)：1738-1742.

[6] 全涌，顾明，陈斌.外形几何参数对低矮建筑双坡屋盖升力系数极值的影响[J].建筑结构学报，2011，32(4)：33-38.

[7] 孙高勇，姚勇，李明.低层双坡屋面风压标准k-ε模型模拟研究[J].西南科技大学学报，2013，28(1)：25-30.

[8] 李晓鹏，董志勇.表面圆柱形突体流动特性的数值模拟[J].浙江工业大学学报，2011,39(2)：219-223.

[9] 张兆鑫，赵元虎，徐奔驰.基于CFD法的小型风机非扭曲叶片气动性能分析[J].浙江工业大学学报，2013,41(1)：68-72.

[10] 马剑，程国标，毛亚郎.基于CFD技术的群体建筑风环境研究[J].浙江工业大学学报，2007,35(3)：351-354.

[11] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社，2004.

[12] 陶文铨.数值传热学[M].2版.西安：西安交通大学出版社，2001.

[13] HOXEY P， RICHARDS R P L， SHORT J. Wind pressures on a 6m cube[J]. Journal of Wind Engineering and Industrial Aerodynics，2001，89(8)：1553-1564.

[14] 黄本才，汪丛军.结构抗风分析原理及应用[M].2版.上海：同济大学出版社，2008.

[15] 孙少鹏，杨岞生.非结构化网格生成技术的研究[J].空气动力学学报，1996，14(1)：19-25.

[16] DELAUNARY D， LAKEHAL D， PIERRAT D. Numerical approach for wind loads prediction on buildings and structures[J]. Journal of Wind Engineering and Industrial Aerodynics，1995，57：307-321.

[17] 孙瑛，武岳，沈世钊,等.大跨平屋盖表面的特征湍流研究[J].空气动力学学报，2007，25(3)：319-324.