J-Boolean like 环的扩张

秦 蕊

(杭州师范大学理学院，浙江 杭州 310036)

环R为Boolean-like环,如果R是特征为2的交换环并且对所有a,b∈R都有ab(1-a)(1-b)=0.早在1946年Foster就将Boolean环推广为Boolean-like环[1],之后Swaminathan对其进一步完善[2].而在1951年,Samuel Bourne对Jacobson根有了初步说明[3].

文章将Boolean-like环扩展为J-Boolean like环,即设J(R)是环R的Jacobson根,如果对环R中任意元素a,b都有(a-a2)(b-b2)∈J(R),那么R称为J-Boolean like环.之后又研究了J-Boolean like环的性质以及与广义矩阵环、幂级数环和Morita Context环间的关系.

文中所有的环都是有单位元的环(交换环或非交换环),C(R)表示环R的中心,J(R)、U(R)分别表示环R的Jacobson根和单位元.

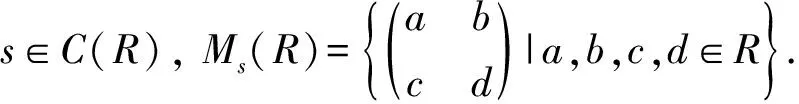
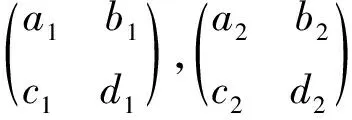
这样,Ms(R)在R上构成一个广义矩阵环[4].

定义2设R是有单位元的环, 若取R中任意元素a,b,都有(a-a2)(b-b2)∈J(R),那么R称为J-Boolean like环.

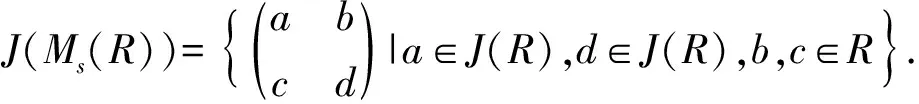
证明见参考文献[5].

定理1在环R中任取s∈J(R)∩C(R), 则R为J-Boolean like环当且仅当Ms(R)为J-Boolean like环.

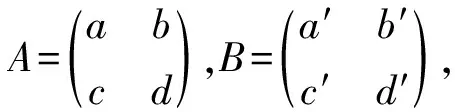
这里

P=(a-a2-sbc)(a′-a′2-sb′c′)+s(b-ab-bd)(c′-c′a′-d′c′)=

(a-a2)(a′-a′2)-(a-a2)sb′c′-sbc(a′-a′2)+sbcsb′c′+s(b-ab-bd)(c′-c′a′-d′c′),

Q=s(c-ca-dc)(b′-a′b′-b′d′)+(d-d2-scb)(d′-d′2-sc′b′)=

s(c-ca-dc)(b′-a′b′-b′d′)+(d-d2)(d′-d′2)-(d-d2)sc′b′-scb(d′-d′2)+scbsc′b′,

由于R是J-Boolean like环, 可得(a-a2)(a′-a′2)∈J(R),(d-d2)(d′-d′2)∈J(R),而s∈J(R)∩C(R),所以P∈J(R),Q∈J(R).根据引理1可以得到(A-A2)(B-B2)∈J(Ms(R)),也就是环Ms(R)是一个J-Boolean like环.

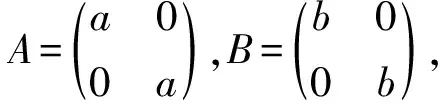
引理2[6]在幂级数环R[[x]]中,J(R[[x]])={f(x)∈R[[x]]|f(0)∈J(R)}.

定理2R是J-Boolean like环当且仅当幂级数环R[[x1,x2,…,xn]]也是J-Boolean like环.

证明(⟹)只需证n=1时的情况.在环S=R[[x]]中任取

f=a0+a1x+a2x2+…+anxn+…,h=b0+b1x+b2x2+…+bnxn+…,

可以得到

进而

(⟸)任取a,b∈R, 显然a,b∈R[[x]],进而有(a-a2)(b-b2)∈J(R),进一步由归纳法可知,R[[x1,x2,…,xn]]是J-Boolean like环.

推论1设环R中,(x)是x生成的主理想整环, 则R是J-Boolean like环当且仅当

是J-Boolean like环.

例1设Z4是一个J-Boolean like环, (x)是x生成的主理想整环, 则M(x)(Z4[[x]])是一个J-Boolean like环.

众所周知, 广义矩阵环是Morita Context环的特殊形式, 以下来讨论Morita Context环的有关内容及若干与J-Boolean like环的联系.

定义3若(R,S,V,W,ψ，φ)包含了两个环R,S,两个双模RVS,SWR,和一对双模同态ψ:V⊗SW→R,φ:W⊗RV→S,满足条件:

1)ψ是R-双模,中间S-线性映射.即有

Rψ(v⊗Sw)=ψ(Rv⊗Sw),ψ(v⊗Sw)R=ψ(v⊗SwR),ψ(vS⊗Sw)=ψ(v⊗Sw).

2)φ是S-双模,中间R-线性映射.即有

Sφ(w⊗Rv)=φ(Sw⊗Rv),φ(w⊗Rv)S=φ(w⊗RvS),φ(wR⊗Rv)=φ(w⊗Rv).

3)ψ(v⊗Sw)v′=vφ(w⊗Rv′),φ(w⊗Rv)w′=wψ(v⊗Sw′).

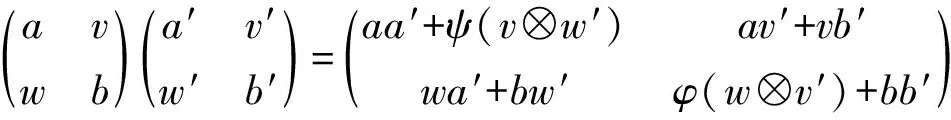
作为一个环, 称为Morita Context环[7].

引理3在Morita Context环T=(R,S,M,N,φ,ψ)中,当φ=ψ=0时,有

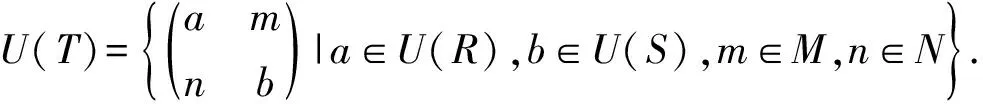
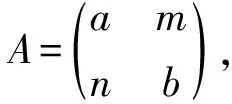
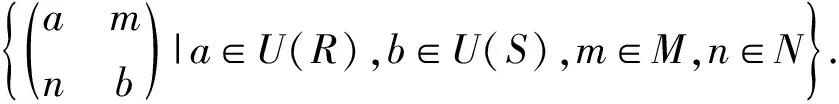
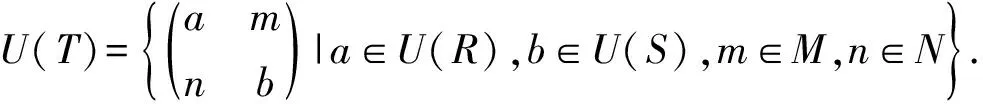
引理4在Morita Context环T=(R,S,M,N,φ,ψ)中, 当φ=ψ=0时, 有

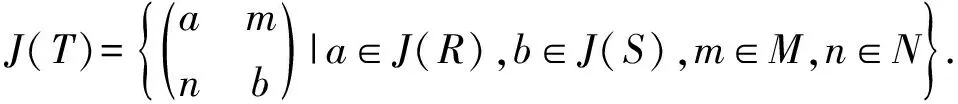
引理5设e是环R中的幂等元, 则有eJ(R)e=J(eRe)[8].

引理6设R是J-Boolean like环,e是环R中的幂等元, 那么eRe也是一个J-Boolean like环.

证明任取eae∈eRe,ebe∈eRe, 从而eae,ebe∈R, 由于R是J-Boolean like环, 所以有(eae-(eae)2)(ebe-(ebe)2)∈J(R),因此(eae-(eae)2)(ebe-(ebe)2)=e(eae-(eae)2)(ebe-(ebe)2)e∈eJ(R)e,由引理5,(eae-(eae)2)(ebe-(ebe)2)∈J(eRe),所以eRe是J-Boolean like环.

定理3在Morita Context环T=(R,S,M,N,φ,ψ)中, 如果φ=ψ=0, 那么R,S都是J-Boolean like环当且仅当T也是J-Boolean like环.

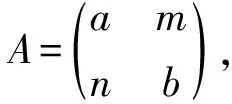
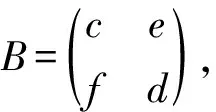
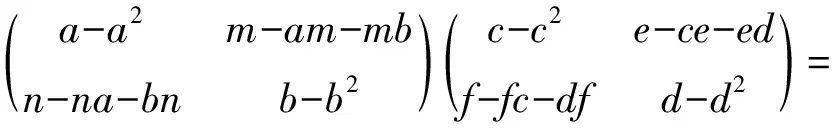
因为R,S是J-Boolean like环, 所以(a-a2)(c-c2)∈J(R),(b-b2)(d-d2)∈J(S).再由引理3知(A-A2)(B-B2)∈J(T),所以T是J-Boolean like环.

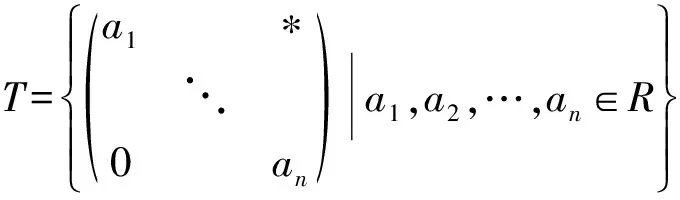
引理7设R是一个J-Boolean like环, 那么R的任意一个同态像都是J-Boolean like环.

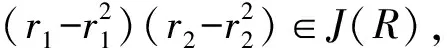
推论3环R是J-Boolean like环当且仅当R[[x]]/(xn)也是一个J-Boolean like环.

证明(⟹)由已知,R是J-Boolean like环,根据定理2有,R[[x]]即是J-Boolean like环,再由引理7得到,R[[x]]/(xn)也是一个J-Boolean like环.

(⟸) 设

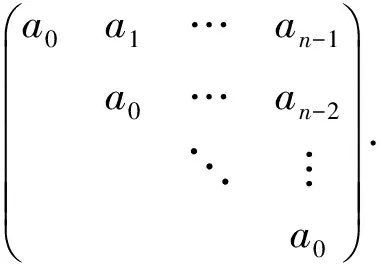
显然,σ是定义良好且保持单位元, 下证σ保持加法, 保持乘法.

任取R[[x]]中元素g(x)=b0+b1x+…bnxn+…,则有f(x)+g(x)=(a0+b0)+(a1+b1)x+…(an+bn)xn+…,进而

所以σ保持加法.f(x)g(x)=c0+c1x+…cnxn+…,这里ck=akb0+ak-1b1+ak-2b2+…+a0bk,k=0,1,2,…,所以

从而σ保持乘法, 进而σ是环同态, 且为满同态.根据环同构定理有R[[x]]/Kerσ≅Tn(R).

下证Kerσ=(xn).

Kerσ={f(x)|σ(f(x))=0}={f(x)=a0+a1x+…+anxn+…|σ(f(x))=0}=

{f(x)=a0+a1x+…+anxn+…|a0=a1=…=an-1=0}=

{f(x)=anxn+an+1xn+1+…}={f(x)=xnF(x)}=(xn).

这里F(x)为关于x的多项式, 所以R[[x]]/(xn)≅Tn(R).由于R[[x]]/(xn)是J-Boolean like环, 所以Tn(R)是J-Boolean like环, 再由推论2知,R是J-Boolean like环.

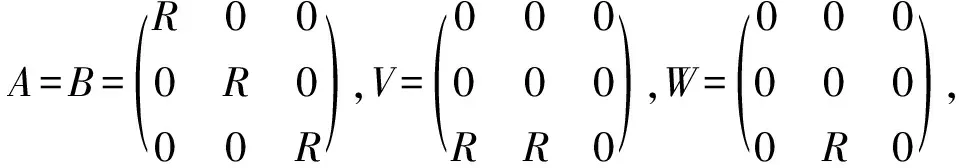
ψ:V⊗BW→A,ψ(V,W)=VW,φ:W⊗AV→B,φ(W,V)=WV,

[1] Foster A L.The theory of Boolean-like rings [J].Transactions of the American Mathematical Society, 1946, 59(1):166-187.

[2] Swaminathan V.On Foster’s Boolean-like rings [J].Math Seminar Note, 1980, 8(2):347-367.

[3] Samuel Bourne.The Jacobson radical of a semiring [J].Proc Natl Acad Sci USA, 1951, 37(3):163-170.

[4] Tang G H, Zhou Y Q.Staong cleanness of generalized matrix rings over a local ring [J].Linear Algebra and Its Applications, 2012, 437:2346-2559.

[5] Krylov P A, Tuganbaev A A.Modules over formal matrix rings [J].Math Sci, 2010,171(2):248-295.

[6] Lam T Y.A first course in noncommutative rings, GTM131 [M].2nd ed.New York:Spring-Verlag, 2001:78.

[7] 卢燕骅.关于Morita Context环的若干研究 [D].杭州：浙江大学, 2007.

[8] Rowen L H.Ring theory:Vol I[M].New York :Academic Press, 1988:183.