基于SD的组团式城市交通生成预测理论方法研究
张 燕,严 凌
(上海理工大学 管理学院,上海 200093)
组团式的城市格局与国内大多数“摊大饼”式的城市格局相比,可以防止城市规模过大所造成的交通堵塞,环境恶化等问题,既有高效率,又可保持良好的自然生态环境的较为理想的城市结构。多中心组团式格局已经逐渐成为国内城市形态的发展趋势[4]。
组团式城市的形成和发展与经济的空间组织密不可分,相关的区域研究开始于19 世纪初杜能提出的农业区位理论,以1826年出版的《农业和过敏经济中孤立国》一书为代表,系统的提出了农业布局的区位理论。杜能所设想的是一个由周围农村的农民提供供应品的孤立城市。随着19世纪近代工业的大发展,从19世纪下半叶起,工业区位理论逐渐成为古典区位理论研究的主流[5]。1885年德国学者龙哈德(W.launhard)发表《过敏经济学说的数学论证》,提出了工业企业布局因素中的“重量三角形”和“价格漏斗模型”。1993年,克里斯塔勒(W.Christaller)《德国南部的中心论》一书中首次发表了这一理论。首先界定了中心地、中心地功能和中心度的概念,提出了不同等级其中心度划分的基本依据[1-4]。
现状交通调查和传统的交通需求预测方法在宏观指导性和现实实用性方面已难以适应复杂的组团式城市交通生成预测的需求,因此预测方法上需要有新的思路和突破。
从最初地理条件的限制,城市由距离比较近的几个团块发展到现在强调主要考虑功能分区的组团式布局。以及传统城市的发展模式在规模扩大中,诸如中心区人口密度大,用地紧张,交通堵塞,居住幸福指数降低的诸多弊端,组团式的发展布局为此提供了启示。组团式城市在发展的过程中以往的预测交通生成方法基于某个因素如城市土地利用性质,或者人口难以较全面的说明影响,对组团式城市交通生成有影响的不光有城市土地利用性质、人口,还有诸如交通设施能力,城市规模,产业规模等。作为交通系统规划的前提,而交通生成又是四阶段法(Trip generation-Trip distribution-Modal split-Traffic assignment)的第一步。本文将城市土地利用性质,城市组团中心数目,人口,经济发展四者纳入组团式城市交通生成预测的系统动力学模型中,为组团式交通生成的预测提供更为严谨,可行的影响因素,力求达到本文所用的方法预模拟预测出的数据误差在10%以内。[5-9]。
1 系统动力学方法
1956年,美国麻省理工学院的福瑞斯特(Jay Forrester W)创立了系统动力学(System Dynamics,以下简称SD。这种方法的基础是反馈控制理论、手段是计算机仿真技术、主要应用于社会经济复杂系统定量研究,经由建立反馈环和设定各个变量之间的方程关系来实现的。1980年,我国引进SD,并在1986年首次召开了全国SD学术交流会,此后关于SD的研究并应用到了诸多领域,并取得了学术与实践上的发展与进步[10-12]。
在城市交通领域,国内基于系统动力学有王云鹏对道路运输量进行预测的研究[13]、许长新等对港口吞吐量预测模型的构建[14]、叶英等人对区域社会经济发展的预测研究[15]、姜洋对城市交通治堵方案提出与优化[16]、张林峰、范炳全等人对交通影响下对城市中心演化做了模型构建于仿真研究[17],交通生成预测不是一个新的话题,可以说被研究烂的课题,但运用系统动力学方法还很少有研究,SD模型是建立在控制论、系统论和信息论基础上研究反馈系统结构、功能和动态行为的一类模型,其突出特点是能够反映复杂系统结构、功能与动态行为之间的相互作用关系,对复杂系统进行动态仿真实验,从而考察复杂系统在不同情景(不同参数或不同策略因素)下的变化行为和趋势,提供决策支持。
但是,将SD应用与交通生成预测的研究还不是很多,SD在预测方面有诸多优势,比如考虑因素较全面,功能与动态行为之间的相互作用关系大部分可以用方程表示出来,前提是处理好他们之间的量纲,函数转换关系,而且还试图涵盖社会经济方面的各个内容,但也比较复杂本文主要针对这方面做研究,力求组团式城市的交通生成预测精确与可行简洁,避免以往模型强调仿真结果、强调参数的设置、强调对定量模拟结果的重视,却缺乏对模型框架的深入阐述,致使模拟过程变得复杂与进行不下去。
2 组团式各中心交通影响范围
各组团中心是组团内部的经济力集中点,对其周围交通小区的影响力的不等,可以借助引力场理论进行模拟,各个组团的可达性可通过牛顿的势能公式来确定。在此,本文将组团布局模式各中心交通吸引范围的问题简化为形式
(1)
式中:Iij为i小区与j小区之间的相互作用量,其中i=1,2,…,m;j=1,2,…,n;Q为i小区的工作岗位规模;Qj为小区的人口数或其它质量指标;dij为i小区与j小区之间的距离km;α,β,γ及K均为常数,这些常数可以通过抽样调查的方法取得。几个交通小区之间联系量的实际数据,经过多元回归得到。在Qi,Qj及dij已知的情况下,可以求出城市内某组团中心i和任一交通小区j的相互作用量,然后通过下面的公式可以求得j与组团中心小区相互联系的相对强度
(2)
Fij也可以看作j小区对于组团中心小区i的吸引范围的隶属度,根据择大的原则,就可以确定每一个小区j分别属于哪一个组团中心小区i的最大吸引范围。在此基础上,就得到各个组团中心的最大吸引范围,该模型可用于多组团模式的城市各中心交通影响范围的界定[18]。
根据现在我国或者外国出现的城市组团式形式,可以概括为3类:多中心组团式布局、边缘组团式布局、混合组团式布局。其城市交通系统结构逻辑图分别如图1所示[19]。
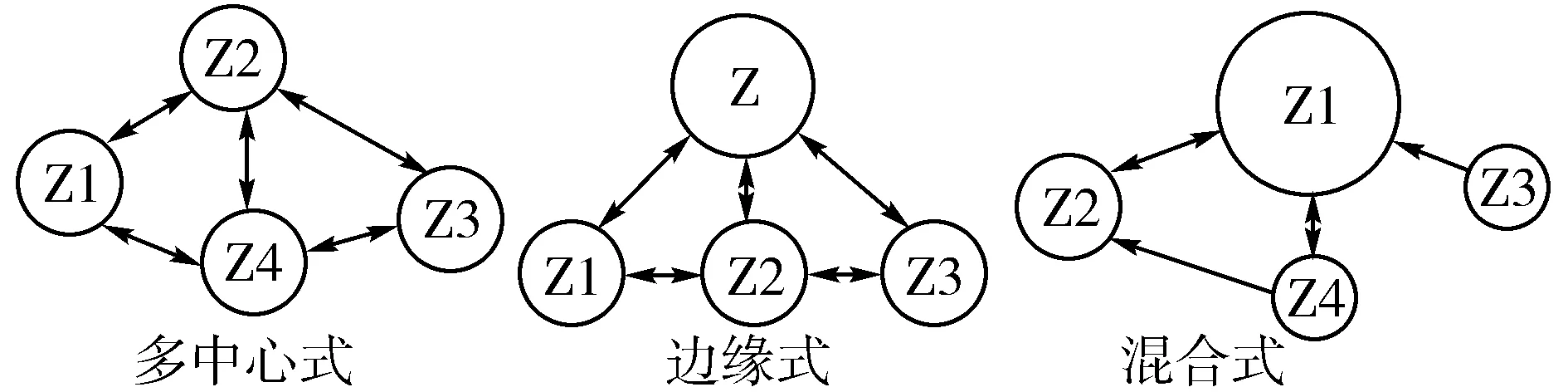
图1 三种形式的组团式布局城市交通系统结构逻辑图
当两个商业中心时,因为城市中心基本上作为商业集聚区,为了便于分析城市中心之间的相互作用,就暂时忽略居民的影响。假设两个城市中心的商业规模分别为y1=y1(t)和y2=y2(t),均是时间t的连续可导函数,且均为密度限制的,可以建立如下的系统动力学模型:
(3)
式中,a1,a2,a3,b1,b2,b3均为正的常数,λ1和λ2为城市中心1和2的交通对商业规模的影响系数。
平衡点1、2、3其实都不是想看到的,也不是现在大多数城市追求的城市发展未来,而平衡点4表示,两个城市中心间商业的竞争处于平衡点上,也就是组团式城市中的多中心布局,这种布局方式更有利于节约资源,符合城市的可持续发展状态。将这种模型应用到多个中心相互作用的特大城市中,将更趋复杂,因此要建立更为细致的模型,由于各个中心交通设施服务能力不同,交通可达性系数不同,而良好的交通系统对商业活动是具有促进作用的。根据上述分析,建立多中心的相互作用SD模型为:
(4)
式中:ai0,ai1x,ai2,bi0,bi1,bi2,cij均为正的常数,λi为城市中心i的交通对商业规模的影响系数,M为城市的总人口。
3 组团式城市预测模型的建立
3.1 建立仿真模型
3.1.1 仿真模型流程图
根据系统动力学解决问题的几个步骤建立组团式城市交通生成预测系统动力学模型流程图如图2所示。
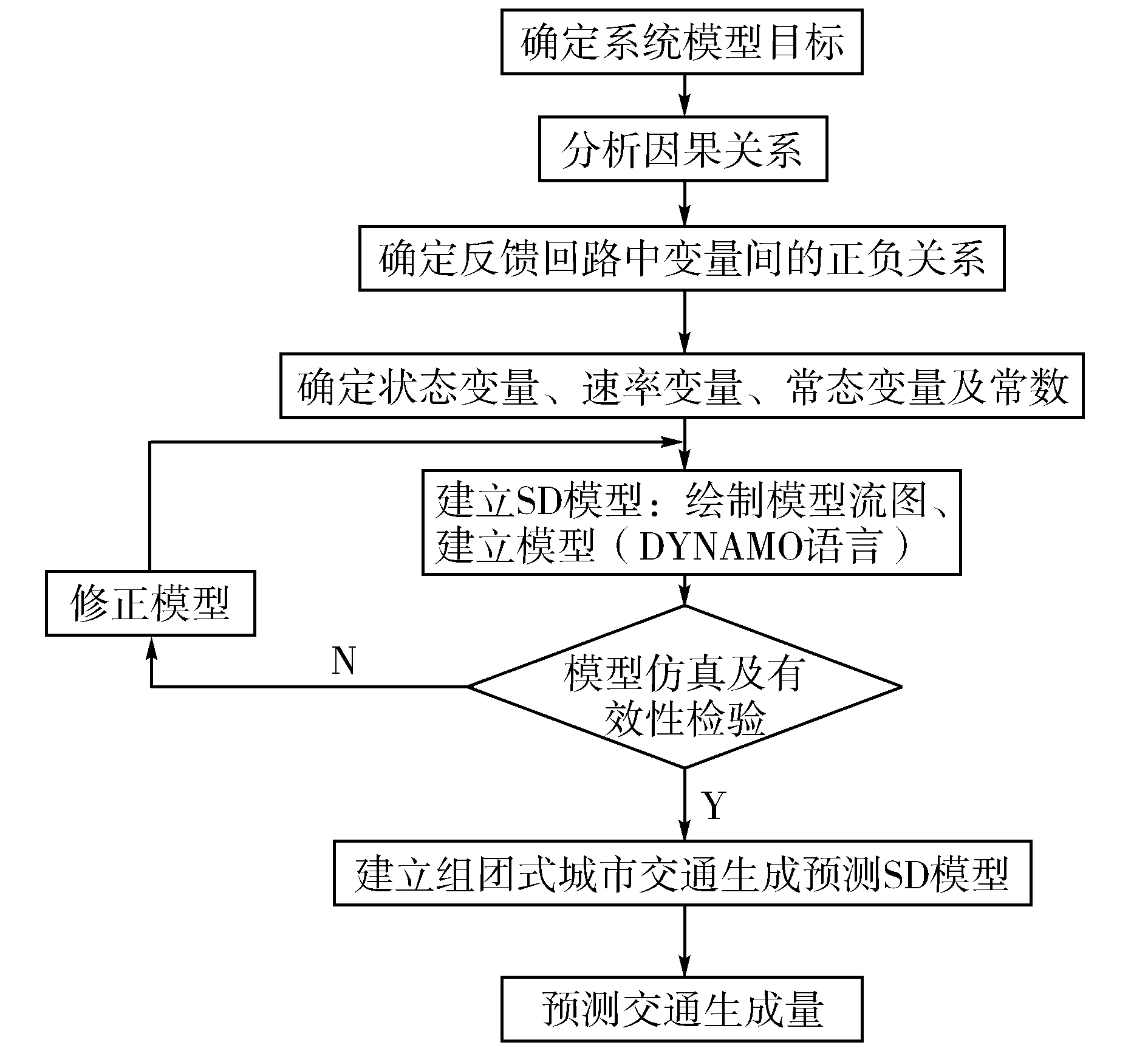
图2 组团式城市交通生成预测建模流程图[14]
3.1.2 交通生成量预测因果关系图
经过系统分析,建立组团式城市交通生成预测系统因果反馈图如图3所示。此图可以比较直观的反应出整个组团式内部要素之间动态的发展机制。
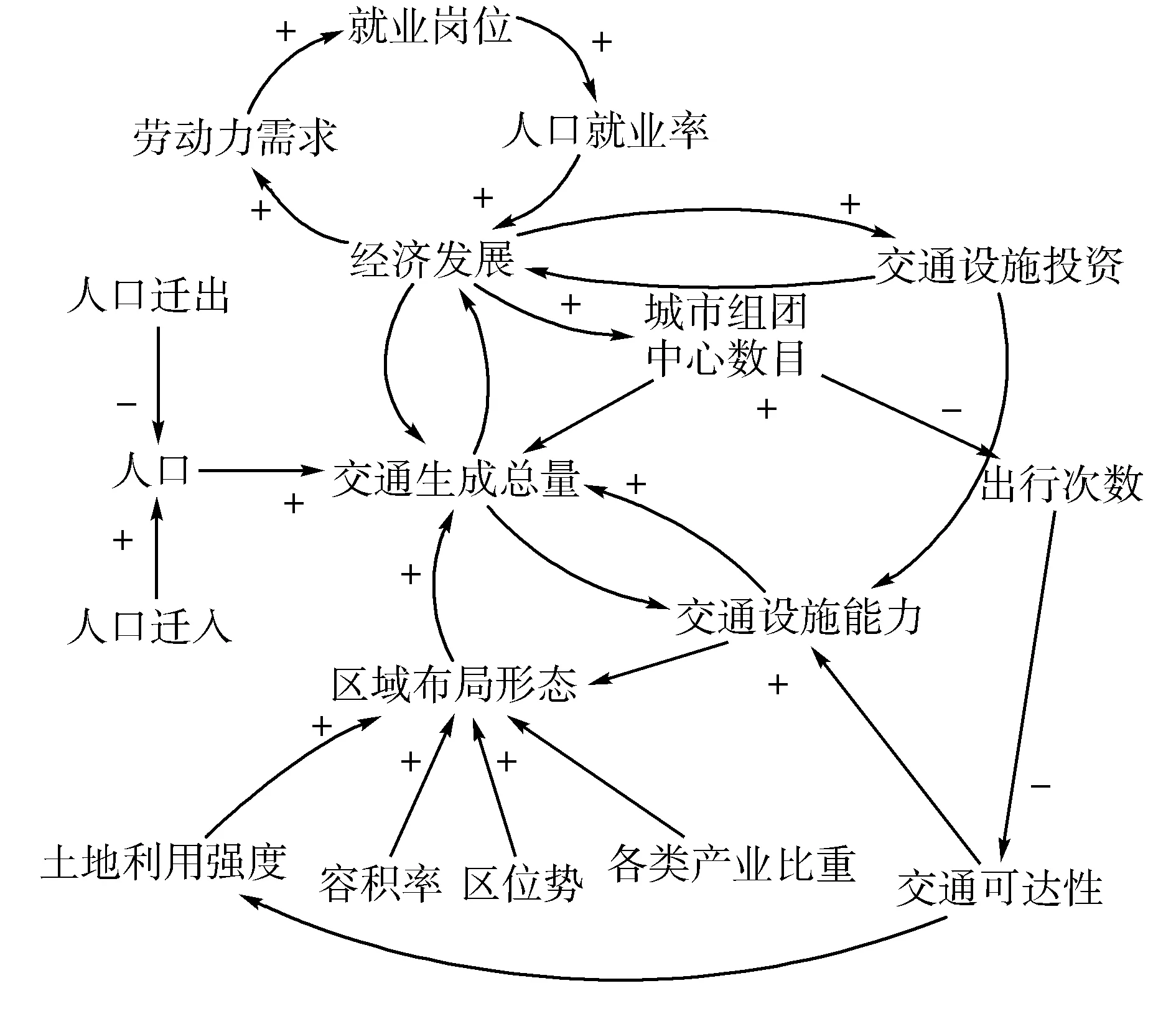
图3 组团式城市交通生成预测因果关系图
因果反馈环能够清楚地表达系统中各要素之间的定性关系,因此,因果反馈环的确定是系统动力学研究中的关键。
反馈环一:经济发展-劳动力需求-人口就业率-经济发展
反馈环二:交通生成总量-经济发展-交通设施投资-交通设施能力-交通生成总量
反馈环三:交通生成总量-经济发展-城市组团中心数目-出行次数-交通可达性-土地利用强度-区域布局形态-交通生成总量
反馈环四:交通生成总量-城市组团中心数目-出行次数-交通可达性-交通设施能力-交通生成总量[20]
3.1.3 指标体系
组团式城市预测模型的指标体系见表1[21]。

表1 预测组团式城市交通生成量仿真模型的指标体系
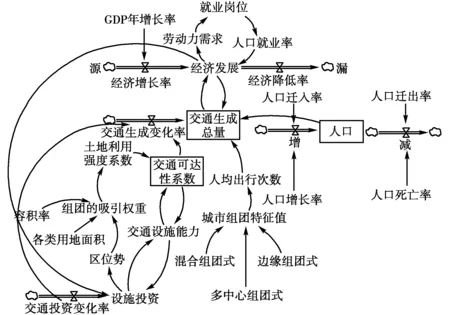
图4 组团式城市交通生成量预测系统动力学模型
3.1.4 模型涉及到的主要方程
SD流图只说明了系统中各变量间的逻辑关系与系统构造,但不能显示他们的定量关系,因此需要建立系统动力学方程,如图4所示。以下是这个模型中主要涉及到的方程(L为状态方程,R为速率方程,A为辅助方程,T为表函数)[22、24]。
L交通生成总量=人口×人均出行次数×(1+交通生成变化率)
L人口总数=INTEG(+人口增加值-人口减少值,初始值)+净移入量
A人均出行次数=人均出行次数JK×cos(城市组团中心数目特征值+1.5)(0,π)
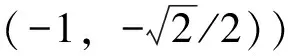
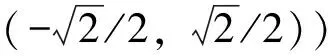
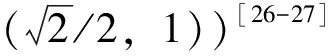
A人均GDP=LGDP/总人数
LGDP=INTEG(+GDP增加值-GDP减少值)
TGDP年增长率表=WIHTLOOPUP(time,数组)
RGDP增加值=GDP年增长率表(time)
R交通生成变化率KL=(交通可达性系数-1)×(1+交通设施投资增长率K)+人口增长率×λ
交通可达性系数=f(土地利用强度系数,组团的吸引权重)
某组团的吸引权重Ki=组团的面积×组团的出行吸引权重×组团的土地利用强度系数/∑(组团的面积×组团的出行吸引权重×团的土地利用强度系数)[23]
第i个组团土地利用强度系数(下标含义如上)。
(5)
式中:Mri是第i个组团居住用地强度系数,SRij是第I个组团第j块居住用地面积km2,VRrij是第i个组团第j块居住用地的容积率。
关于城市组团特征值的确定:田宇对组团式居民人均出行次数表现为反“S”型的变化趋势,即高端平台——快速下降——低端平台三个阶段的研究,本文利用cosx函数来为其赋值。本文不同用地性质的权重取值,见表2。
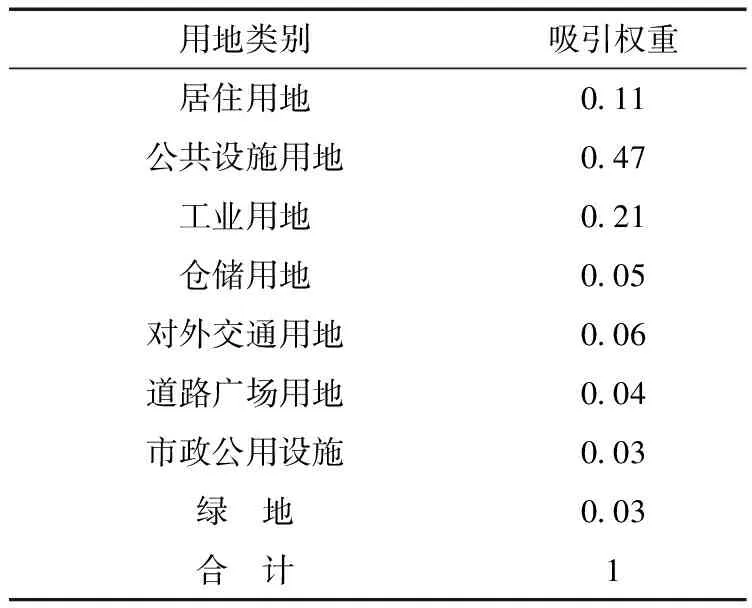
表2 用地性质权重的不同取值
4 模型仿真与结果分析
图5 永嘉县与假设的组团式地理位置分布图
系统动力学模型参数的确定方法有观察法、经验法、估计法、拟合法、试验寻优法等。由于人口增长率、经济发展率、各个产值比重、交通设施投资这些数据比较容易获得,但类似于交通设施服务能力、交通可达性、区位势等数据通过弹性系数法,传统的统计方法进行标定。
模型的仿真结果与一般常用的人均出行次数常用标准进行对比分析如表,从表中可以看出两者误差小于10%,说明SD模型能够较好的预测组团式城市交通生成,模型对系统的模拟是值得信赖的,研究过程中还采用了传统的预测统计方法,系数标定法,建立了各个因素之间的方程关系,用于与SD模型进行对比分析,验证其科学性、可行性。
以弹性系数法、二元线性回归法为例,计算永嘉县交通生成总量,并分析预测值与统计值的误差,分析结果见表3及表4,所用数据为2013年调查所得,从表中可以看出仿真值与统计值误差基本上在10%以内,证明了此次将主要四大因素用到SD模型里的可行性与有效性。
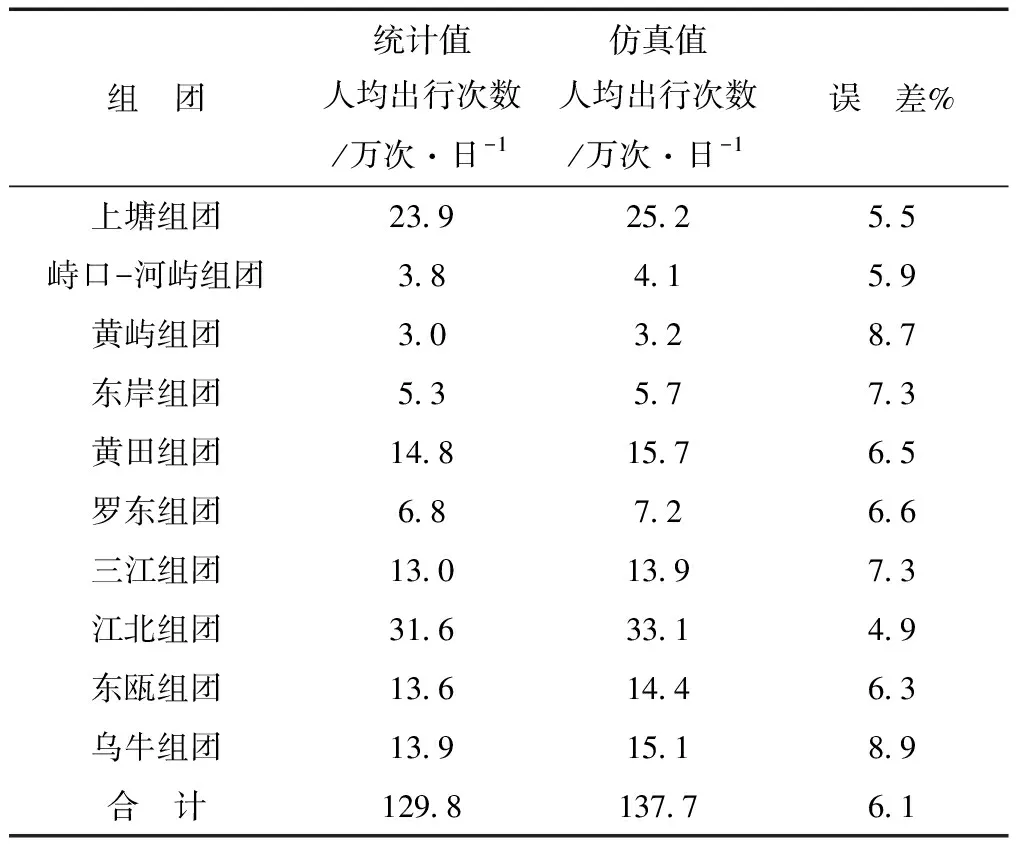
表3 永嘉县交通生成SD模型预测误差分析表
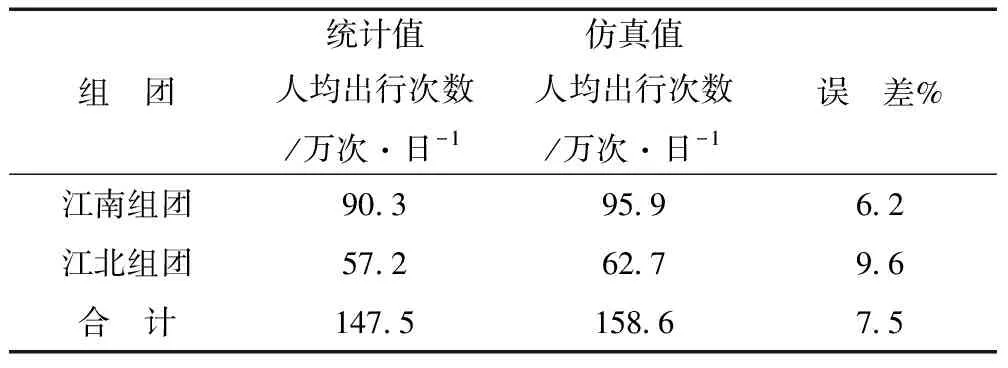
表4 假设的交通生成SD模型预测误差分析表
5 模型的检验与评估
(1)检验模型的合理性与有效性
将前面本文所构建的方程,及SD模型用VENSIM软件运行,并基于此软件的编译检错跟踪功能检验模型的正确性,并观测运行结果证明了模型的合理性,模拟后误差在10%以内,克制拟合程度是良好的。
(2)检验参数灵敏度
在取本文所描述的参数值范围内取不同的参数值,得知这种多次赋值的结果对模型行为的影响很小,在一定的随机干扰情况下,软件也可以实现特定的目标,从而验证了模型的参数灵敏度。
(3)检验方程式极端条件
为了便于了解非线性特性,以及查出模型中的弱点,在变量可能变化的极端条件下对方程式进行检验,特别是针对速率方程,要对其进行严格的检验,通过检验结果发现本文中我们所构建的方程都是可以再研究中应用到的。
6 结束语
本研究将系统动力学方法用于组团式城市的各种影响因素及其内在关系的定性分析中,并建立系统动力学模型对组团式城市交通生成预测进行动态预测和定量分析。与传统方法相比,该模型不仅考虑城市土地利用、人口等常规因素,而且考虑城市组团中心数目及经济等更多的影响因素,能较系统地反映出系统各影响因素间的相互关系。通过对永嘉县和假设的组团式城市系统进行仿真分析,验证了该模型的实用性和有效性。
【参 考 文 献】
[1]刘俊良,臧景红,何延青.系统动力学模型用于城市需水量预测[J].中国给水排水,2005,21(6):31-34
[2]刘秉镰,杨 明.城市物流园区需求预测的系统动力学模型构建[J].城市交通,2009,7(5):21-26.
[3]杨 敏,陈学武,王 炜,等.基于人口和土地利用的城市新区交通生成预测模型[J].东南大学学报,2005,35(5):815-819.
[4]翟长旭.组团式城市交通特性分析及发展策略——以重庆市主城区为例[J].重庆交通大学学报,2012,12(3):9-11.
[5]杨晓立.大城市组团式间交通联系方式选择的研究[D].西安:西安建筑科技大学,2001
[6]李昆达,杨新苗,郭一麟.快速城镇化下组团式城市的大运量公共交通系统建设[J].城市交通,2013(3):31-36.
[7]杨 敏,李文勇,陈学武,等.城市交通生成预测实用分析模型及其应用[J].公路交通科技,2005,22(12):109-112
[8]Beckman M J.Location Theory[M].New York:Random House,1968.
[9]Meyer M D.Transport planning for urban areas:A retrospective look and future prospects[J].Journal of Advanced Transportation,2000,34(1):143-171.
[10]彭震伟.区域研究与区域规划[M].上海:同济大学出版社,1998.
[11]张国伍.交通运输系统动力学[M].成都:西南交通大学出版社,1993.
[12]王其藩.系统动力学[M].北京:清华大学出版社,1994.
[13]王云鹏,杨志发,李世武,等.基于系统动力学的道路运输量预测模型[J].吉林大学学报(工学版),2005,35(4):426-430.
[14]许长新,严以新,张 萍.基于系统动力学的港口吞吐量预测模型[J].水运工程,2006(5):26-28.
[15]叶 英,范炳全.区域社会经济发展的系统动力学模型研究——以上海宝山区为例[J].上海经济研究,2007(5):106-112.
[16]姜 洋.系统动力学视角下中国城市交通拥堵对策思考[J].城市规划,2011,35(11):73-80.
[17]张林峰,范炳全,严广乐,等.交通影响下的城市中心演化系统动力学模型及仿真研究[J].系统工程,2004,22(5):61-65
[18]陈 新,杨 雪,杨 珺,等.城市用地形态与城市交通布局模式研究[J].经济经纬,2005(3):64-66.
[19]田 宇.基于功能布局的组团城市交通出行特征分析[D].重庆:重庆交通大学,2010.
[20]Giuliano G,Small K A.Is the journey to work explained by urban structure?[J].Urban Studies,1993(9):1450-1500.
[21]董艳华.基于系统动力学的城市群交通规划方法研究[J].交通运输系统工程与信息,2011,11(3):8-13.
[22]Kitamura R,Mokhtaria n P L,Laidet L.A micro analysis of land use and travel in five neighborhoods in the San Francisco Bay Area[J].Transportation,1997,24:125-158.
[23]石 飞,江 薇,王 炜,等.基于土地利用形态的交通生成预测理论方法研究[J].土木工程学报,2005,38(3):115-118.
[24]李 江,段 杰.组团式城市外部空间形态分形特征研究[J].经济地理,2004,24(1):61-66.
[25]李 娟,石建军,吴子啸.组团式城市居民出行特征变化趋势分析[J].交通运输工程与信息学报,2008,6(4):70-75
[26]Anas A,Arnott R,Small K A.Urban spatial structure[R].The University of California Transportation Center,1997.
[27]陈瑶瑶,马健霄.城市交通交通环境影响评价指标体系[J].森林工程,2012,28(1):59-62.

