基于细水雾作用的原木楞堆温度场的相关性研究

薛 伟，耿志伟

(东北林业大学 工程技术学院，哈尔滨 150040)

目前，细水雾灭火技术已广泛应用于城市消防，在贮木场消防方面的应用也进入了原木楞堆灭火特性的实验研究阶段。房玉东[1]等研究了受限空间内细水雾灭火过程中温度场的降温速率与喷头距离的三维变化关系，发现温度与喷头距离呈指数负相关；薛伟[2-3]等定点研究了原木楞堆在细水雾灭火过程中的温度场变化，总结了各点的温度变化速率；牛国庆[4]等利用红外影像技术研究了油池在细水雾作用下的温度变化规律，发现受限空间内温度趋于均匀一致。自然环境下贮木场原木楞堆一旦起火，在风的影响下不同点的温度变化很难预测，给贮木场的其他原木楞堆带来了严重威胁[5]。为此，进一步研究楞堆典型位置之间的温度相关性变化规律，利用回归性准确预测整个楞堆温度场的未来变化，对于保障林区贮木场的安全生产具有远大的实际意义。

本论文在自然条件下对原木楞堆进行细水雾灭火实验，以典型位置的温度场为研究对象，逐步分析测点间温度变化的相关性以及线性回归性，通过一个点的温度可以立即精确预测出其他方位的温度，为今后细水雾在贮木场原木楞堆消防的实际应用提供理论指导及实验依据。

1 研究环境

为了接近现实贮木场原木楞堆消防灭火的情形，灭火实验在自然环境下原木楞堆易燃的春季进行。细水雾灭火实验进行10次，最后的实验数据需要利用数理统计取平均值.实验主要器材包括：细水雾灭火系统、原木楞堆、K型热电偶、数据采集系统和数据处理系统等。其中将选用的K型热电耦命名为T1～T7，T1、T2、T3、T4、T5、T6、T7分别布置于楞堆的前部、后部、右侧、左侧、底层、中层和顶层；细水雾灭火系统主要由储水泵、氮气罐、液压阀、气压阀和细水雾喷头组成，喷头采用的是XWT型多喷嘴型两相流细水雾喷头，保护范围为流量系数k=3.5，雾通量为50 L/min，雾化锥角为120° 。引燃物为汽油，实验前将8 L汽油均匀的喷洒在原木楞堆的表面，灭火实验时喷头安装在原木楞堆顶端中部正上方5 m[6-7]处，即O点；原木楞堆选用的是落叶松，具体参数见表1。

表1 试验统计参数

热能通过空气的热传导而四处传播[8-9]，为了得到有效的实验数据必须排除过近距离的热能互相干扰现象，所以热电偶的三维空间的布置必须合理，图1为实验装置示意图。

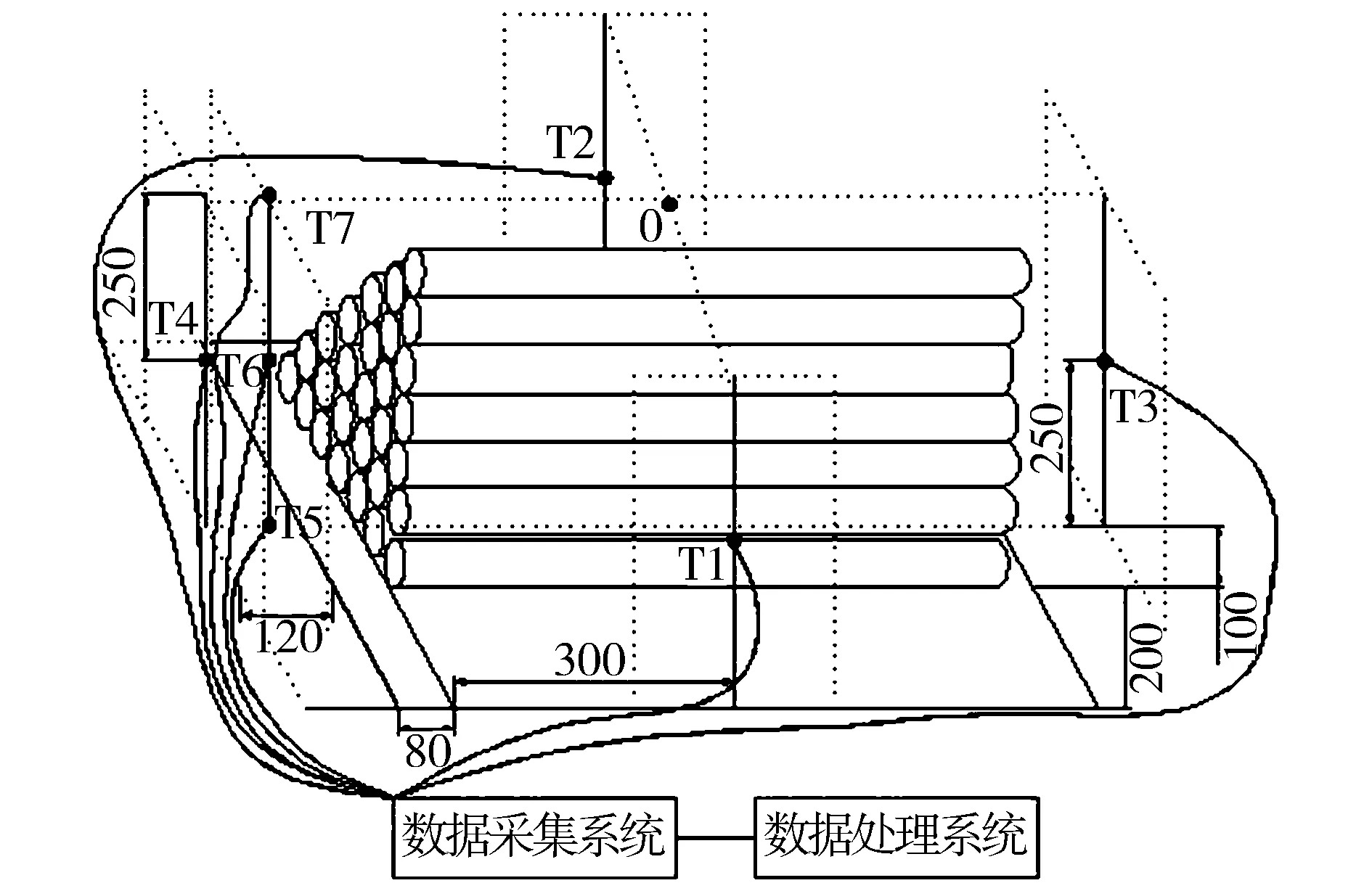
图1 实验装置示意图/cm

2 研究内容及结果分析

2.1 相关性分析

原木楞堆的燃烧过程被分为4个阶段：初始燃烧、蔓延燃烧、稳定燃烧和衰减熄灭[10]。细水雾开始作用于原木楞堆的时间须在原木楞堆处于稳定燃烧的阶段，薛伟教授曾研究楞堆燃烧达到这一阶段需要1 100 s左右，本实验由于受原木数量、长度和湿度等影响，在976 s时已经出现了大量的明火，此时已经达到了稳定燃烧的阶段，所以本实验在原木楞堆稳定燃烧的第1 080 s施加细水雾。实验进行10次，最后利用数理统计取平均值即可[11]。

SPSS是一款集数据处理专业性、数理统计分析灵活性的软件，本论文利用SPSS对本实验得到的数据进行相关性分析、回归性分析。为了方便用SPSS软件处理采集到的T1～T7的数据，在进行数据输入时，用编号A、B、C、D、E、F、G分别代替T1、T2、T3、T4、T5、T6、T7测得的数据。首先将输入的数据做初步的相关性分析，因为这些数据的散点图符合正态分布，所以利用SPSS做Pearson相关性分析，得到原木楞堆7个部位之间的皮尔逊相关系数：RA，B=0.880、RA，D=0.870、RB，D=0.831、RC，E=0.865、RC，F=0.872、RC，G=0.834、RE，F=0.807、RE，G=0.858、RF，G=0.931。当∣R∣≥0.8时两变量高度相关，P值=0.000时，变量又进一步显著线性相关。变量A、B、D之间具有高度线性相关性，同时变量C、E、F、G之间也具有显著线性相关性。所以原木楞堆的前部、后部和左侧之间的温度场存在一个显著的线性回归方程，其右侧、底层、中层和顶层也有一个显著的线性回归方程。为了下一步的多元统计线性回归分析，将变量A、B、D与变量C、E、F、G分别作线性回归分析。

2.2 线性回归分析

对原木楞堆的前部、后部、左侧之间的温度场变化做线性回归分析，利用多元统计分析的数理统计原理，建立线性回归方程的数学模型。

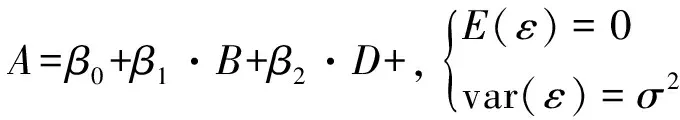
其中β0为回归常数，β1、β2为回归系数，ε为随机误差，表示其他不可观测的随机因素(风向、湿度和光照强度等)的影响造成的误差，ε为一个随机变量。在本实验实际问题研究中为了方便对线性方程的回归方程显著性检验、回归系数检验以及其他假设检验，假设ε 服从正态分布。

本实验得到了251组数据，样本容量大于变量数量这就进一步提高了回归方程的准确性。对于得到的251组数据(Bi，Di；Ai)(i=1，2，…，251)，则线性回归模型可表示为

i,j=1,2,…,251。

利用SPSS软件，做逐步回归分析，具体结果见表2。

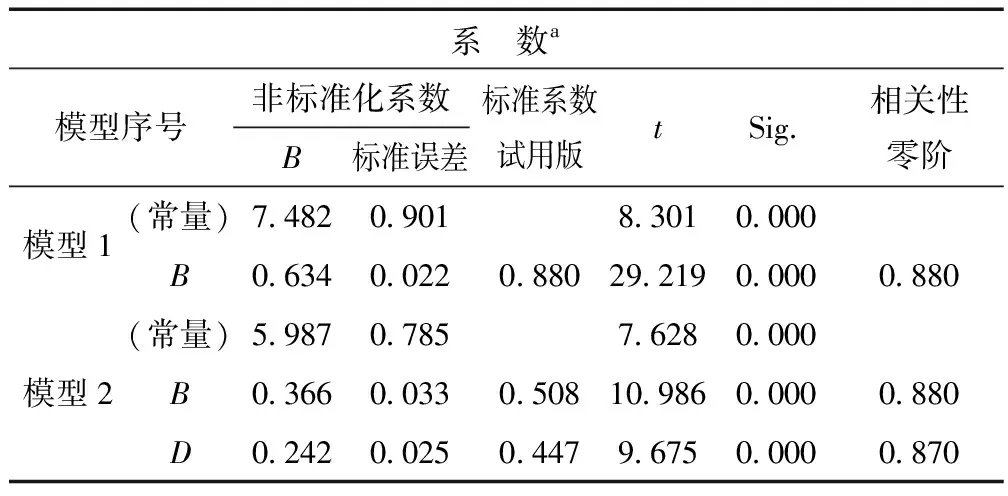
表2 系数相关阵

注：B—方程非标准化系数；t—t检验系数；sig—显著性检验系数

从表2系数相关阵可以看出原木楞堆前部温度场关于其后部、左侧的温度场线性回归方程如下：

未标准化模型2方程：前部温度=5.987+0.366×后部温度+0.242×左侧温度。

标准化模型2方程：前部温度=：0.508×后部温度+0.447×左侧温度。

回归方程的F检验中，F服从自由度为(2，251-2-1)的F分布，临界值F0.05(2，251-2-1)=3.875。软件方差分析中F=632.433>3.875，显著性p=0.000<0.005为高度显著，所以原木楞堆后部温度、左侧温度对前部温度产生了显著的线性影响，回归方程显著；线性回归方程的前提条件是假设ε具有零均值和等方差，服从正态分布且互相独立，为了排除非此情况，有必要对回归方程做随机误差ε的自相关性DW检验 。本实验样本容量n=251，解释变量k=3，查DW检验上下界表得：dl=1.78，du=1.81。软件处理数据得到的DW=1.848，du<1.848<4-du，证明该回归方程随机误差的确服从正态分布且互相独立，方程假设成立。当其他条件不变时，原木楞堆后侧温度增加，其前部的温度会提高；左侧温度升高时也会导致其前部的温度提高。

同理，对原木楞堆的右侧、下层、中层、底层之间的温度场变化做线性回归分析，建立线性回归方程的数学模型。

设因变量C与自变量E、F、G的多元线性回归模型为

利用SPSS对251组数据进行逐步回归分析得到结果见表3。

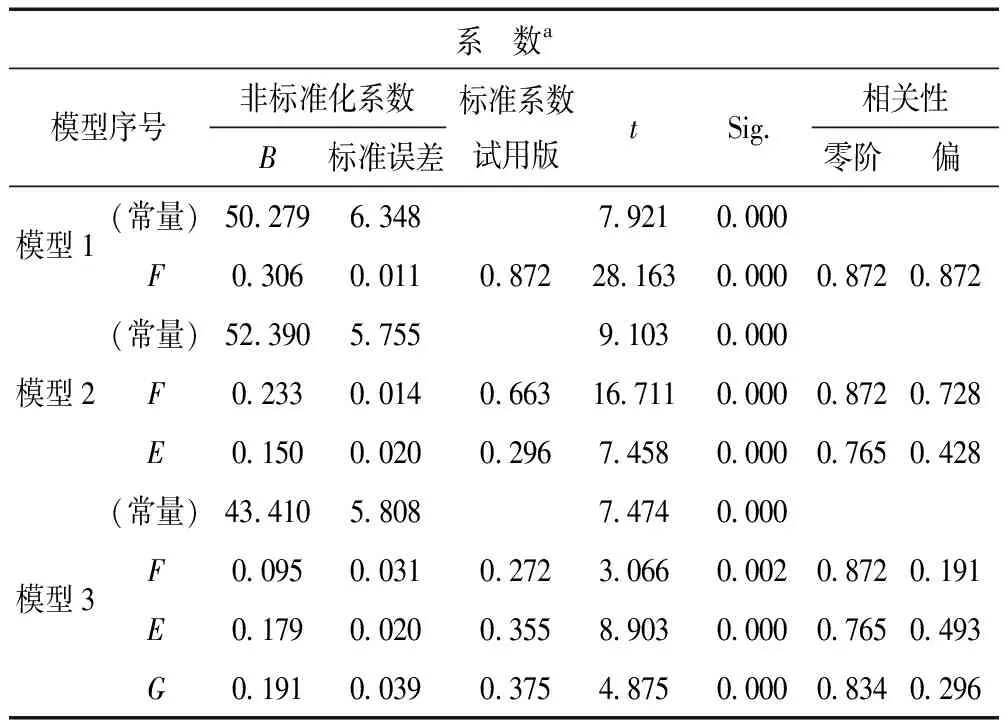
表3 系数相关阵

经过逐步回归，从表3系数相关阵可以看出原木楞堆右侧温度场关于其底层、中层、顶层的温度场线性回归方程如下：

未标准化模型3方程：右侧温度=43.410+0.095×中层温度+0.179×下层温度+0.191×上层温度。

标准化模型3方程：右侧温度=0.272×中层温度+0.355×下层温度+0.375×上层温度。

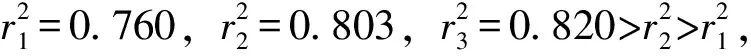
回归方程的F检验中，F服从自由度为(3，251-3-1)的F分布，临界值F0.05(3，251-3-1)=2.6。软件方差分析中F=380.156>2.6，显著性p=0.000<0.005为高度显著，所以原木楞堆顶层温度、中层温度、底层温度对右侧温度产生了显著的线性影响，回归方程显著；同理对回归方程做随机误差ε的自相关性DW检验 。n=251，解释变量k=4，查DW检验表得：а=0.05时，dl=1.77，du=1.82。软件处理数据得到的DW=2.01，du<1.848<4-du，证明该回归方程随机误差的确服从正态分布且互相独立，方程假设成立。当其他条件不变时，原木楞堆顶层温度、中层温度、底层温度的增加，都会直接导致其前部的温度提高。

3 结 论

(1)细水雾作用下的原木楞堆温度场的前部、后部、左侧之间有显著的相关性；原木楞堆温度场的左侧、顶层、中层、底层之间也有较高的相关性。

(2)细水雾作用下原木楞堆温度场的前部与其后部、左侧之间存在两元线性回归方程，并且通过了t、F等相关检验，标准化后方程：前部温度=0.508×后部温度+0.447×左侧温度；原木楞堆温度场的右侧与其顶层、中层、底层之间存在三元线性回归方程，通过检验后的标准化方程为：右侧温度=0.272×中层温度+0.355×下层温度+0.375×上层温度。

【参 考 文 献】

[1]方玉东，苏国锋，林 霖，等.受限空间细水雾作用下烟气温度变化规律研究[J].自然科学进展，2008，18(4)：475-480.

[2]薛 伟，李双玉.细水雾作用下原木楞堆燃烧温度场研究[J].消防科学与技术，2012，3(9)：913-915.

[3]薛 伟，王 储.细水雾作用下原木楞堆燃烧特性的实验研究[J].热科学与技术，2012，11(4)：331-335.

[4]牛国庆，余明高，徐志胜，等.细水雾作用下受限空间油池火焰温度分布实验研究[J].河南理工大学学报，2007，26(1)：6-10.

[5]卞 伟，薛 伟.贮木场楞堆火灾的实验研究[J].森林工程，2006，22(5)：1-4.

[6]谢安桓.闭式高压细水雾喷头的研究[D].杭州：浙江大学，2011.

[7]廖义德.高压细水雾灭火系统关键技术及其灭火性能研究[D].武汉：华中科技大学，2008.

[8]葛晓霞，张学魁.细水雾灭火系统技术研究进展[J].火灾科学，2006，5(2)：74-77.

[9]丛北华，蔡志刚，陈吕义，等.细水雾阻隔火焰热辐射的模拟研究[J].中国安全科学学报，2005，15(12)：69- 73.

[10]张光俊.贮木场楞堆燃烧的数值模拟[D].哈尔滨：东北林业大学，2007.

[11]薛 伟，王 储.细水雾作用下原木椤堆燃烧特性的实验研究[J].热科学与技术，2012，11(4)：331-335.