排队论在某家乐福超市服务台优化设计中的应用
范泽超,吴金卓
(东北林业大学 工程技术学院,哈尔滨 150040)
在超市购物方面,人们已经不仅仅满足于商品的质量和种类,对于超市的服务速度和便捷程度的要求也越来越高。因此,作为一个大型连锁超市,研究如何提高服务质量是非常有必要的。超市收银台作为超市连接顾客的重要纽带,在提高超市服务水平、增加竞争力方面有十分重要的地位。由于顾客的到来时间和接受服务时间是一个随机过程,因此该系统是一个随机服务系统。如果超市开放的收银台数目过少,就会造成系统的拥堵,增加顾客的等待时间,造成客户的不满意,甚至客户流失。如果收银台设置的数量过多,虽然可以提高客户的满意度,但超市投资就会增加并导致资源的浪费。因此,超市决策者需要找到其中的平衡点,既能降低企业的成本,使各项资源得到合理使用,又能提高客户的满意度[1]。本文采用排队论理论来考虑服务台数最优设计的问题,通过应用超市收银排队系统优化模型,并以哈尔滨市某家乐福超市为例,优化其在不同时段开放的服务台数。
1 超市排队模型
在超市服务台系统中,顾客到来的时间和数量属于随机分布,而且不同收银服务台的服务时间也属于随机分布,因此,该系统是一个显著的随机排队服务系统。超市收银排队服务系统可以认为是一个具有多服务台、排队规则为先到先服务的M/M/n/∞排队系统[2]。在该系统中,有n个服务台并列工作,顾客按照参数λ(λ>0)的泊松流到达,单个顾客需要的服务时间独立且服从参数μ(μ>0)的负指数分布。该系统中的顾客源可以认为是无限的,并且每个顾客到达该系统都是随机和独立的[3-4]。
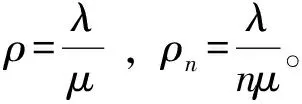
当整个排队系统稳定时,即ρn<1,顾客在系统中的平均等待时间为
(1)
平均等待队长为
(2)
上述方法中计算出的仅仅是该模型的初步参数。实际上,由于不同人在不同情况下对于排队等待时间的容忍度不一样,例如在空闲时间允许排队的时间会长一些,而当时间紧急的时候所能允许的排队时间就会明显缩短。而且,不同的消费人群所允许的排队等待时间和队长也是不一样的。因此,需要获取不同人群的最长等待时间和最长等待队长,在此基础上对该超市排队系统的服务台数量来进行优化,获得各个时段最佳的服务台开放数量,这样既可以提高客户的满意度又能为超市节约成本,增加收益。
设顾客所允许的最长平均等待时间为Tw,所能允许的最长队长为Lw,由此,所能容忍的系统中最长平均等待队长为nLw,由上可得:
(3)
n的最小取值就是服务台数量的最优数,即为:

(4)
由上可得:
(5)
(6)
由此,可以建立相应的超市服务台排队系统的模型[5]。
2 家乐福超市服务台排队系统的模拟及优化
2.1 数据收集
2012年1月到2013年3月,笔者对哈尔滨市某家乐福超市进行数据调查。该超市一共有45个收银台,在工作日和节假日分别进行调查统计,并分15个不同时段进行调查(每5 min为一个单位时段),在每个时段随机抽查其中的400个样本进行统计,整理出观察数据。在非节假日的数据整理见表1、表2和表3。

表1 非节假日顾客到来人数统计频数Ⅰ

表2 非节假日顾客到来人数统计频数Ⅱ
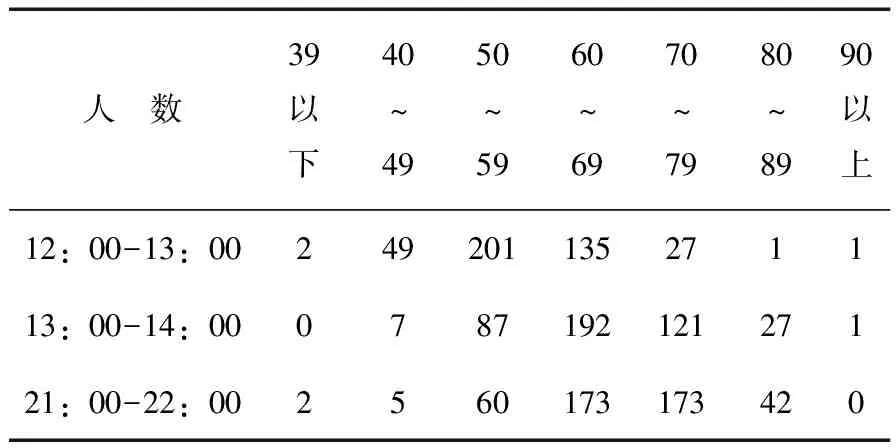
表3 非节假日顾客到来人数统计频数Ⅲ
节假日顾客到来的有关数据整理见表4至表7。

表4 节假日顾客到来人数统计频数Ⅰ

表5 节假日顾客到来人数统计频数Ⅱ

表6 节假日顾客到来人数统计频数Ⅲ
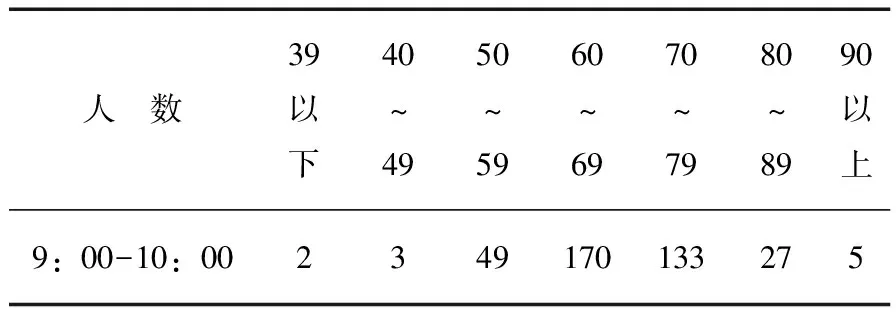
表7 节假日顾客到来人数统计频数Ⅳ
通过对表1至表7中的数据进行统计分析,可以算出顾客的平均到达率,见表8。表9和表10分别为节假日/非节假日各时段顾客的到达率及相应开放的服务台数量。λ1、n1分别表示非节假日顾客到达的均值和相应的各个时段开放的收银服务台数。同样,λ2、n2分别表示节假日顾客到达的均值和相应的各个时段开放的收银服务台数。
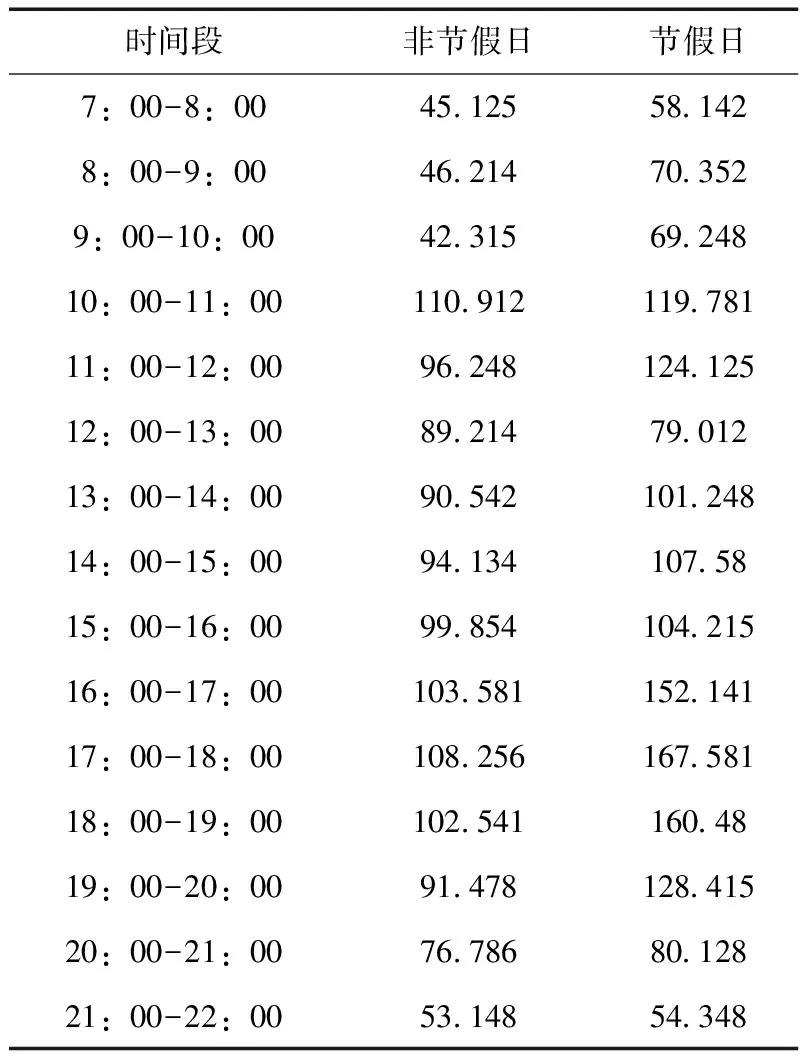
表8 单位时间内顾客的到达率
表9和表10中的数据表明该超市的收银台的开放数目非常不合理。例如,在节假日期间17:00-18:00属于高峰期,然而开放的数目为30,而13:00-14:00为低值期,但是开放的收银台数目同样为30,这就造成了资源的浪费,并且有可能造成高峰期的拥堵,降低服务质量,在其他时段同样存在这样的问题,因此该超市收银台服务系统的设置不够合理,需要对服务台数进行优化。为了研究收银台服务系统中服务员服务顾客的时间的概率分布,在该超市中随机地调查了顾客的服务时间,整理见表11。并且随机调查了一部分消费者,获取其所能容忍的最长的等待时间和等待队长。见表12至表15。
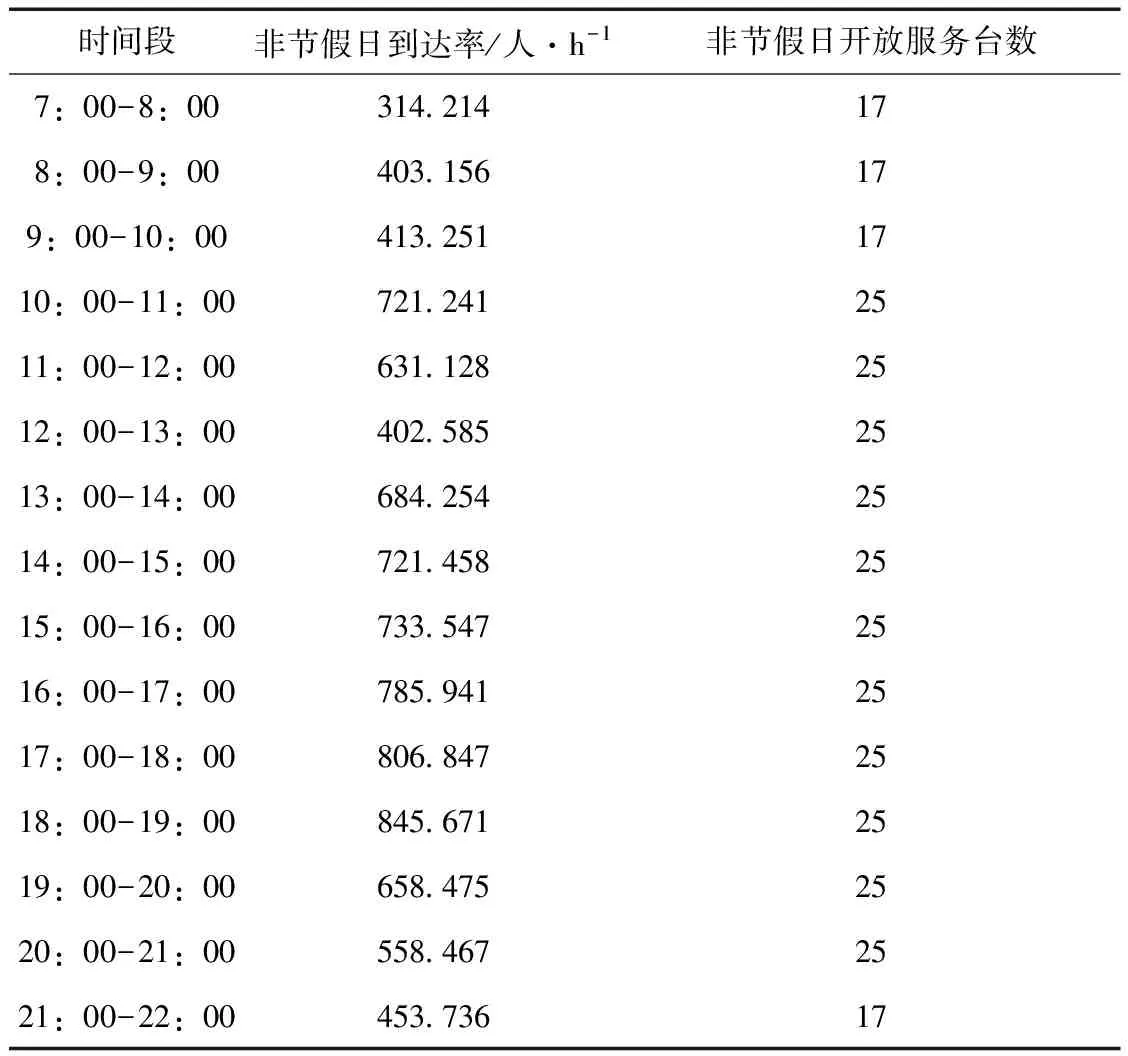
表9 非节假日各时段顾客的到达率及相应开放的服务台数量
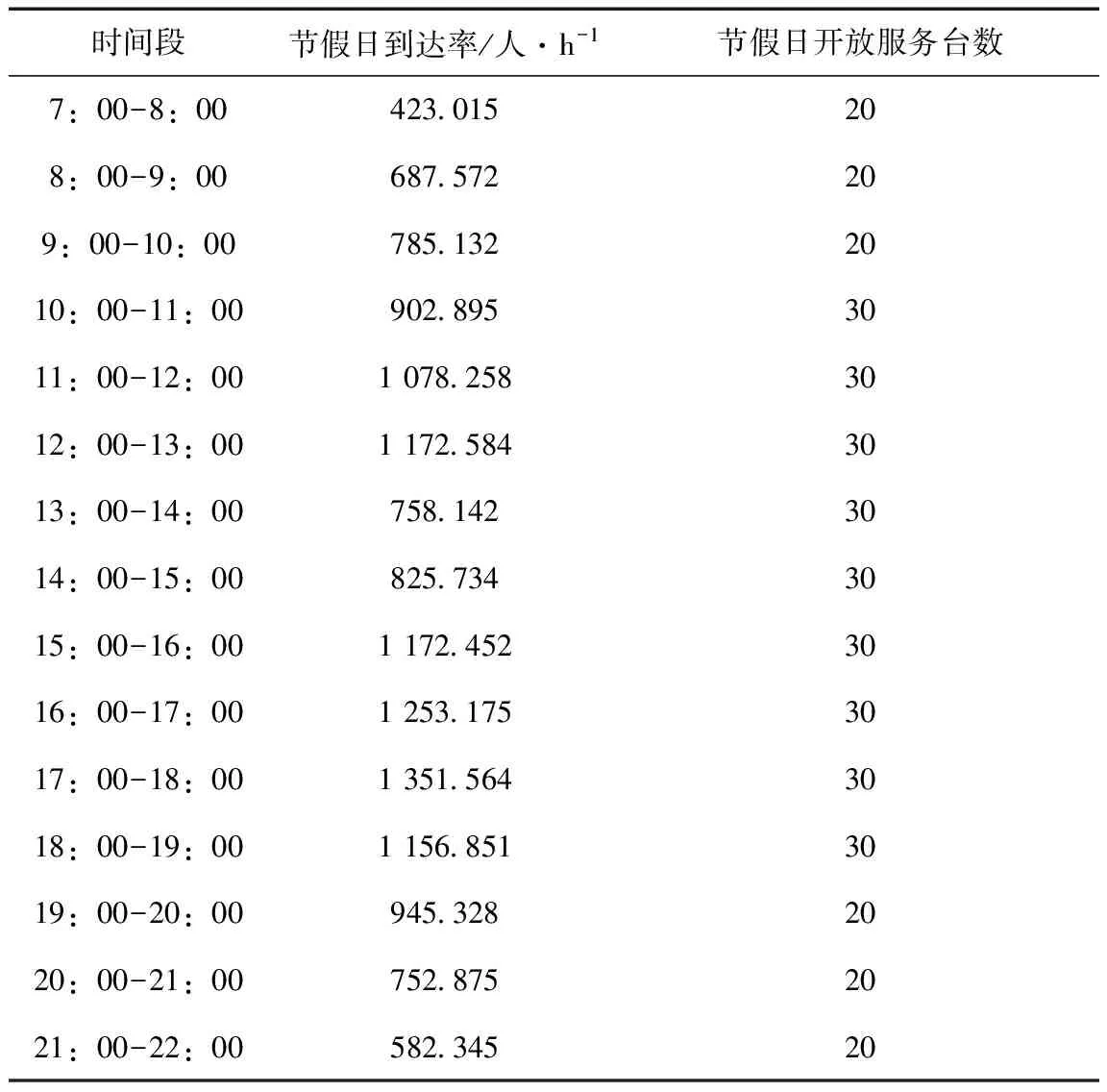
表10 节假日各时段顾客的到达率及相应开放的服务台数量
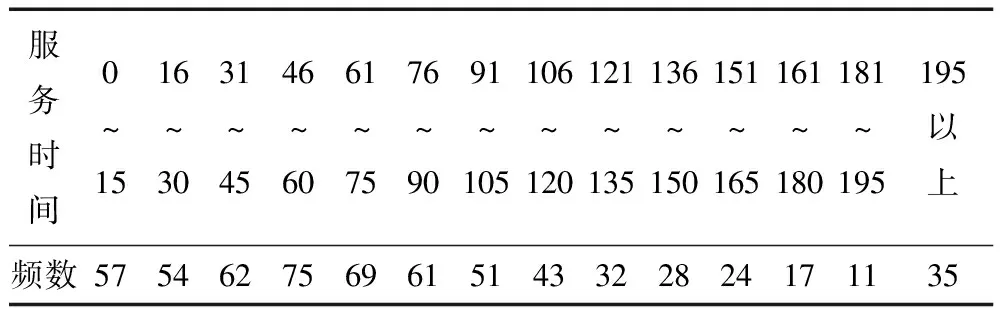
表11 顾客所需的服务时间 s

表12 非节假日所能容忍的最长的等待时间 min

表13 非节假日所能容忍的最长的等待队长

表14 节假日所能容忍的最长的等待时间 min

表15 节假日所能容忍的最长的等待队长 人
根据表12至表15中的数据,可以计算出在非节假日期间顾客所能容忍的最长平均等待时间为6.23 min,最长平均等待队长为7.61人;在节假日期间顾客所能容忍的最长平均等待时间为10.57 min,最长平均等待队长为9.24人。
2.2 顾客到达分布
根据每个时间段的原始数据,分别对其单位时间内即五分钟内到达的顾客数是否服从泊松分布进行检验。本文采用χ2拟合的方法来检验,由于泊松分布中的参数λ是未知的,需要先用极大似然估计法来估计这个参数[6-7]。设总体X服从参数为λ的泊松分布,即
(7)
X1,X2,X3,…Xn是来自总体X的样本,x1,x2,x3,…xn是相对应的样本X1,X2,X3,…Xn中的一个样本值,则样本的极大似然函数为:
(8)
令
可以得到λ的极大似然估计值为
(9)
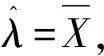
2.3 指标的计算
在2.1中,在非节假日期间顾客所能容忍的最长平均等待时间为6.23 min及最长平均等待队长为7.61人;在节假日期间顾客所能容忍的最长平均等待时间为10.57 min及最长平均等待队长为10.24人。参照表16和表17可以看到,该超市在很多时段所开放的服务台数不合理,存在开放过多和过少的问题,比如在非节假日7:00-8:00,顾客的平均逗留时间为3.08 min,远小于所能容忍的6.23 min,因此在此时就会造成服务台资源的浪费。而在节假日8:00-9:00段,顾客的平均等待时间为16.75 min,平均逗留时间为19.52 min,远远高于顾客所能容忍的最长时间10.57 min,因此,会造成许多不愿等待的顾客的离开,也就造成了顾客的损失。因此,需要对不合理的时段进行优化处理。
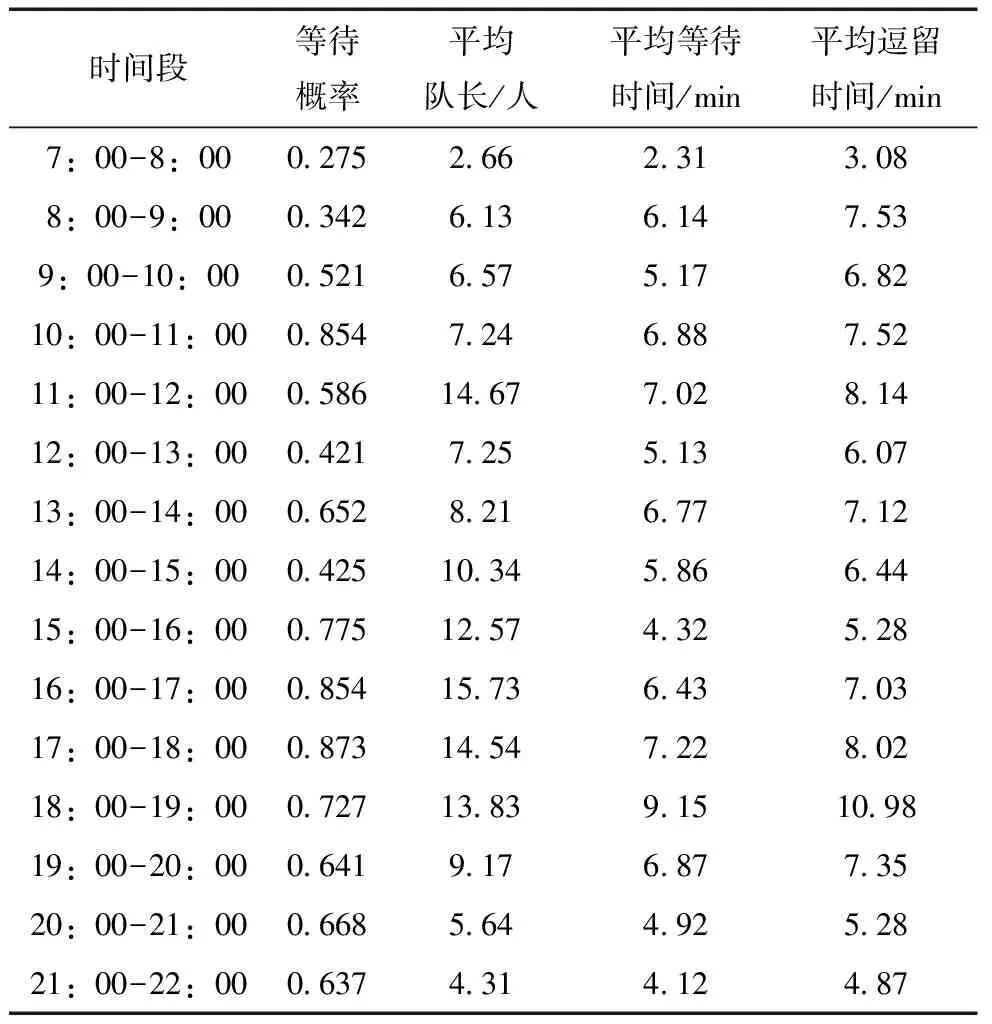
表16 非节假日系统的各项指标
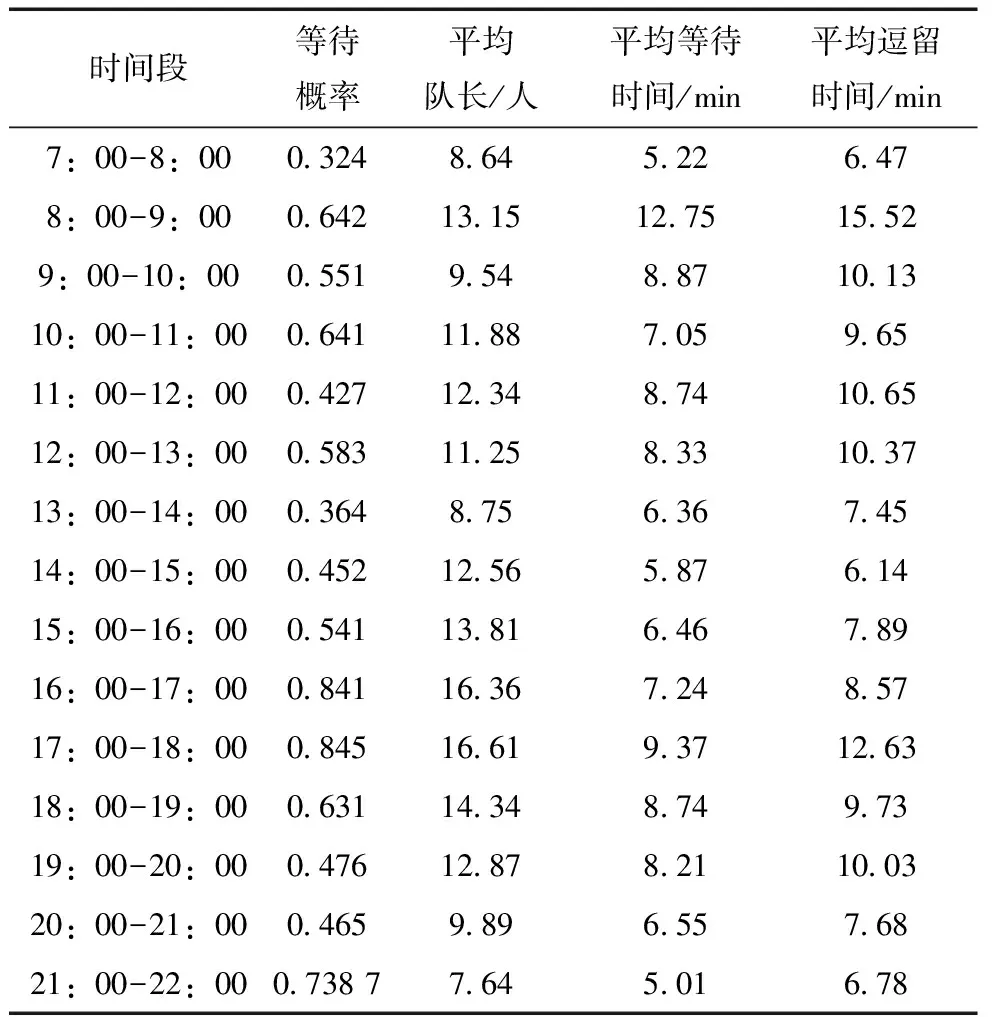
表17 节假日的各项指标
2.4 优化服务台数
本节将对该超市的收银台排队系统进行优化,通过公式


表18 非节假日应开放的服务台数量及相应参数
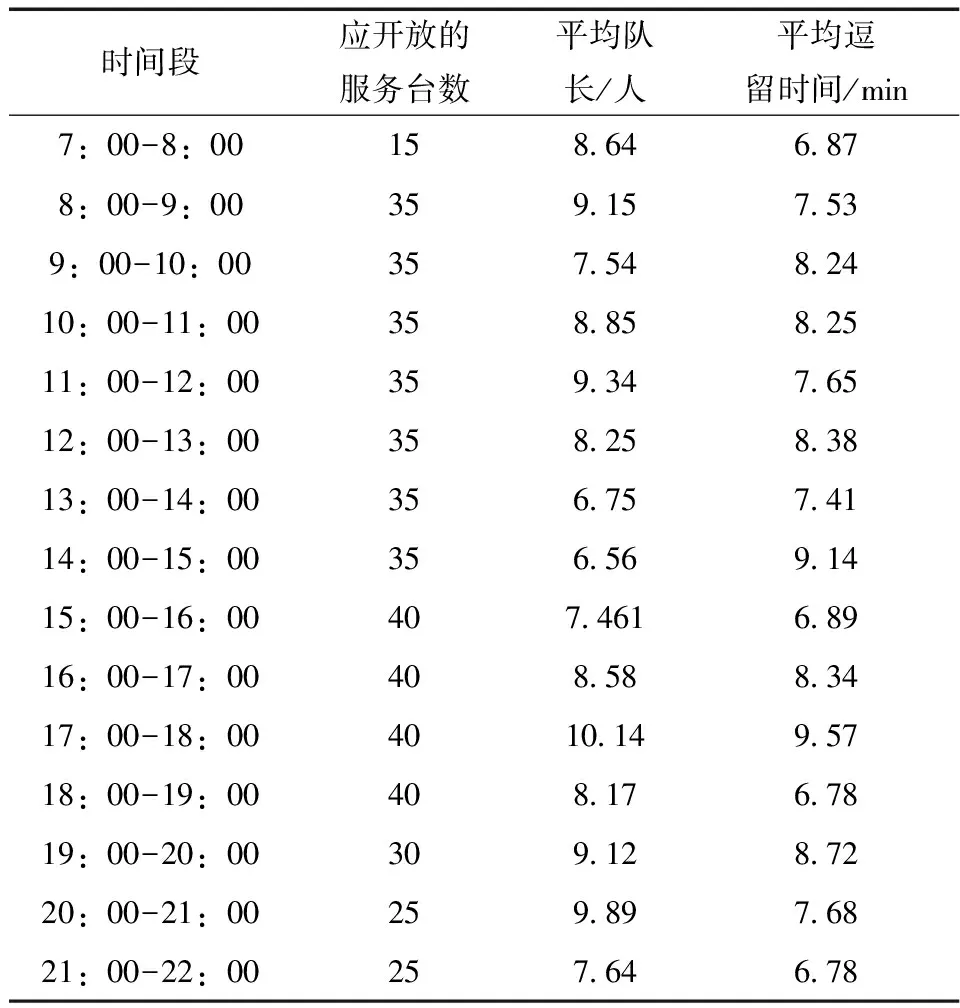
表19 节假日应开放的服务台数量及相应参数
3 结 论
本文以哈尔滨市某家乐福超市为例,运用统计的方法在非节假日和节假日分别对顾客单位时间的到达数量和服务时间进行了统计,并收集顾客所能容忍的最长等待时间和最长等待队长,通过M/M/n/∞模型,算出系统的各项指标。根据计算的数据,指出超市服务台在各时段的开放数目中存在不合理之处,并进行优化,最后给出该超市在非节假日和节假日各个不同时段应该开放的服务台的数目。但是,本文中还有一些不足,期望在以后的工作中能够考虑:
(1)本文中数据的收集还不够精确,因此后续的数据收集在收集方法和收集基数方面应更加精确。
(2)本文中没有考虑到的M/M/n/∞非平衡状态,希望后续能加入非平衡状态的考虑,使结果更加科学准确。
【参 考 文 献】
[1] 米红娟.医院门诊排队网络分析[J].西北师范大学学报(自然科学版),1998,34(2):25-31.
[2] 宋卫斌,苏 秦.虚拟顾客服务系统排队模型[J].管理科学学报,2001,4(3):52-57.
[3] 王丽霞.概率论和随机过程[M].北京:清华大学出版社,2012.
[4] 张雅清.排队论在超市收银服务系统中的应用研究[D].重庆:重庆师范大学,2007.
[5] 彭 杨.物流系统优化与仿真[M].北京:中国物资出版社,2007.
[6] 王 勇,孙 薇,李道华.排队管理系统在银行管理中的应用[J].黑龙江大学自然科学学报,2006,23(2):156-158.
[7] 蔡金凤.基于排队论的大型超市服务台数的最优设计[D].哈尔滨:哈尔滨工业大学,2009.
[8] 郑 欢,古福文.大型超市顾客交费排队系统优化分析[J].管理学报,2005,2(2):171-173.
[9] 冯慧芳.超市收款服务系统的仿真与优化[J].系统工程,2001,19(2):61-65.
[10] 孙 薇.一类排队规则特殊的排队统的分析与应用[D].哈尔滨:哈尔滨工业大学,2005.
[11] 戴维·安德森.数据、模型与决策[M].北京:机械工业出版社,2003.
——国外课堂互动等待时间研究的现状与启示

