木材缺陷的阈值分割算法研究

谢永华，陈庆为

(东北林业大学 机电工程学院，哈尔滨 150040)

木材表面缺陷主要指木材在生长过程中由于客观原因形成的活结、死结和虫眼等变异的组织结构，这些变异的木质结构会影响木材的整体质量和正常性能，通过合理的锯材加工，除去不必要的缺陷组织，不仅可以提高木材利用率，同时也使得木制品的性能得到大大提高。所以，正确地对木材表面缺陷进行识别分类就显得尤为重要。随着模式识别和人工智能的不断发展，运用数字图像处理技术进行木材表面缺陷检测已经成为木材加工行业的一大热门话题，伴随各种图像处理理论的出现，学者们已经提出了千余种木材缺陷检测算法，但是时至今日，在缺陷分割的过程中仍然没有一种通用的分割算法或分割理论，所以，对木材表面缺陷的检测和识别还有很长的路要走[1]。本文从图像阈值分割的角度出发，对多种阈值分割算法的木材图像分割效果进行对比研究。

1 阈值分割算法综述

图像阈值化分割是一种传统的最常用的图像分割方法，它以灰度直方图为处理对象，特别适用于目标和背景占据不同灰度级范围的图像。图像阈值分割就是按照灰度级，选取一个适当阈值对像素集合进行划分，使得到的每个子集形成一个区域，各个区域内部具有一致的属性。而且这样的划分可根据实际情况通过从灰度级出发选取一个或多个阈值来实现。阈值分割以其计算简单、运算效率较高、速度快的优点，被应用于多个领域，成为图像分割中最基本和应用最广泛的分割技术。

常用的阈值分割算法有很多种，大致可以分为两大类：全局阈值分割法和局部阈值分割法。

全局阈值分割方法在图像处理中应用比较多，它在整幅图像内采用固定的阈值分割图像。根据阈值选择方法的不同，可以分为迭代阈值分割法、最大类间方差阈值分割法、最大熵分割法、模糊阈值分割法、共生矩阵分割法、区域生长法等。这些方法都是以图像的灰度直方图为研究对象来确定分割的阈值的。

局部阈值分割法就是将原始图像划分成多个较小的子图像，对每个子图像选取相应的阈值进行图像分割。在阈值分割后，相邻子图像之间的边界处可能产生灰度级的不连续性，因此需用平滑技术进行排除。局部阈值法常用的方法有灰度差直方图法、微分直方图法。

虽然局部阈值分割法能改善分割效果，但是其在使用过程中有很多局限性，比如子图像大小选择要合适，不能太小，还要尽量保证子图像不要完全落入目标区域或背景区域，否则会带来更多无用的干扰信息，另外，其分割速度慢，无法适应实时性要求。本文着重对几种全局阈值分割算法进行研究。

2 几种常用的全局阈值分割算法研究

经典的阈值分割算法是以图像的灰度直方图为研究对象的，尤其适用于具有双峰直方图的图像，双峰直方图如图1所示，对于这样的图像，分割阈值可以选择直方图的两个波峰间的波谷所对应的灰度值作为分割的阈值。

图1 原图、直方图及阈值T分别为35、70、105的分割图象

但是，简单的选取波谷所对应的灰度值作为阈值进行图像分割很多时候并不能得到正确的分割效果，以波谷的灰度值为阈值，有时也并不能将目标和背景图像分开，而且，通常情况下的灰度图像也不一定都具有典型的双峰直方图。基于此，学者们采用不同的方法对阈值选择进行研究，形成了不同的阈值分割算法。

2.1 迭代阈值分割算法

迭代阈值图像分割算法假设图像中出现了两种主要的灰度区域，那么就可以通过反复迭代选取一个最优阈值，将图像分为两部分[2]。具体算法描述如下：

(1)为全局阈值选择一个初始估计值T(图像的平均灰度)。

(2)用T分割图像。产生两组像素：G1由灰度值大于T的像素组成，G2由小于等于T像素组成。

(3)计算G1和G2像素的平均灰度值m1和m2。

(4)计算一个新的阈值：T1=(m1+m2)/ 2。

(5)计算连续两次的阈值差：△T=|T-T1|，T=T1。

(6)重复步骤(2)到(4)，直到连续迭代后的T1值和T值间的差△T为零或小于某个精度要求的数值。

2.2 一维最大类间方差阈值分割算法

最大类间方差阈值分割算法又叫大津法，简称OTSU，是由日本学者大津于1979年提出的，是一种自适应的阈值确定方法[3]。大津算法的几个常用公式如下：

假设T为目标与背景的分割阈值，目标所包含的像素点数为N0，占图像比例为w0，平均灰度为u0；背景所包含的像素点数为N1点数占图像比例为w1，平均灰度为u1，图像的大小为M×N，则有：

w0=N0/(M×N)。

(1)

w1=N1/(M×N)。

(2)

N0+N1=M×N。

(3)

w0+w1=1。

(4)

图像的总平均灰度为：

u=w0×u0+w1×u1。

(5)

某一分割阈值T所对应的目标和背景的类间方差公式表示为：

g=w0×(u0-u)2+w1×(u1-u)2。

(6)

T值取从最小灰度值直到最大灰度值的不同值时，图像的类间方差值也不尽相同，求得使公式(6)最大类间方差最大的T的取值，就是最大类间方差阈值分割算法的最佳阈值。因为方差是灰度分布均匀性的一种度量，方差值越大，说明构成图像的两部分差别越大，当部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小，因此使类间方差最大的分割意味着错分概率最小[4]。

2.3 一维最大熵阈值分割算法

熵的概念是1850年由德国物理学家鲁道夫·克劳修斯首次提出的，它用来表示能量在空间中分布的均匀程度，能量分布得越均匀，熵就越大。在数字图像处理和模式识别领域应用广泛，用以表征信息量的大小。

假设p0，p1，p2，p3，…，pm-1分别为图象灰度值为0，1，2，3，…，m-1的像素点出现的概率，则某一灰度i的信息熵Hi为：

Hi=pi×lnpi,i=0,1,2,…,m-1。

(7)

。

(8)

假设n0，n1，n2，n3，…，nm-1分别为灰度值为0，1，2，3，…，m-1的像素点出现的次数，则某一灰度值出现的概率Pi为：

Pi=ni/(M×N),i=0,1,2,…,m-1。

(9)

(10)

其中，M为灰度图象的行数；N为灰度图像的列数；m为图像的灰度级数。

用一维最大熵阈值分割图象，就是选取一个阈值，把图象分成目标和背景两部分，使得一维灰度统计的信息含量最大，信息含量用熵来表征。假设灰度直方图中，灰度低于阈值T的为目标区域，高于阈值T的为背景区域，则各概率在本区域的分布分别为：

目标区域：

。

(11)

Pi=pi/po,i=0,1,2,…,T。

(12)

背景区域：

。

(13)

Pi=pi/pb,i=T+1,T+2,…,m-1。

(14)

则对于数字图像而言，目标和背景区域的熵分别为：

(15)

(16)

所以整幅图像的熵为：H=H0+Hb。

(17)

一维最大熵阈值分割算法就是对于图象求取灰度阈值T，使得H可以取得最大值[5-6]。

3 阈值分割算法的具体实现流程

图2给出了运用阈值分割算法进行木材表面缺陷分割的详细流程。首先利用仪器设备获得木材表面缺陷彩色图像，将彩色图像转化为灰度级为255的灰度图像，然后使用中值滤波算法进行平滑处理，经阈值分割算法处理获得最优分割阈值，使用该阈值对平滑后的灰度图像进行分割得到二值图像，然后经一系列后续处理最终分割出缺陷所在。

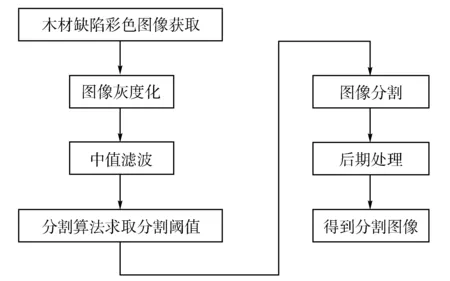
图2 木材缺陷分割算法流程图

4 实验及测试结果

首先收集和获取一些木材缺陷样本彩色图像，所有算法均在Matlab 2013a软件环境下编程实现，首先对彩色图像灰度化处理，然后运用5×5的阈值窗口进行中值滤波，得到的图像经过阈值分割算法获得最佳分割阈值以及分割后的区域图像。

对3种木板材表面缺陷进行了实验测试，这三种缺陷分别是虫眼、死结和活结。具体分割效果如图3所示，最后的二值图像即为分割图像，其中黑色部分为缺陷所在的具体位置。

通过对几种木板材表面缺陷图像的大量实验研究，得出3种算法对于缺陷区域和背景区域具有较强对比度的图像具有非常好的分割效果，比如虫眼一般都呈现一块黑色的暗斑，死结的周围一般也会有一圈暗色区域，对于这两种木板材表面缺陷，3种算法能够准确的分割出来。而对于活结来说，活结部位的灰度值与正常部位灰度值相近，只是纹理的走向稍有不同，此种情况下，最大熵阈值分割算法的分割效果变差，只能够分割出活结部位的裂纹，而迭代阈值分割算法分割效果稍好，不过分割出的活结多呈现环形嵌套的纹理区域，最大方差阈值分割效果最好。从图3中也可看出，最大熵阈值分割对图像的灰度明暗对比度较敏感，而最大方差阈值分割能较好的反映图像的区域特征，迭代阈值分割则介于两者之间。另外，如果木板材表面纹理较浅，该算法能够很好的将其分割。如果活结部位与正常部位灰度差异不大，而且木板材又含有较深的表面纹理，那么该算法就会错误地将木板材的暗纹分割为缺陷区域。

图3 三种分割算法对三种木材缺陷的分割效果对比

5 算法改进

虽然，最大方差阈值分割算法是3种阈值分割算法中性能最好的一个，但是不难看出其分割效果并不是很理想，由于目标和背景区域的对比度的变化，该算法虽然能准确的定位出目标区域，但很多时候不能完全准确的将目标和背景分离，基于此，需要对分割算法进行进一步改进。改进算法的流程如图4所示。

跟据流程图我们很清晰的看出，算法的改进之处在于首先通过最大方差阈值分割算法寻找到最初的最优阈值，然后根据此阈值对图像的灰度级进行压缩，然后再次拉伸灰度级，目的在于增强目标和背景区域的对比度，从而为最大方差阈值分割算法的二次寻优和图象分割作铺垫。

假设中值滤波后原图像的灰度级为255，第一次最大方差阈值分割算法得到的最优阈值为T，则图像灰度级的压缩公式定义如下：

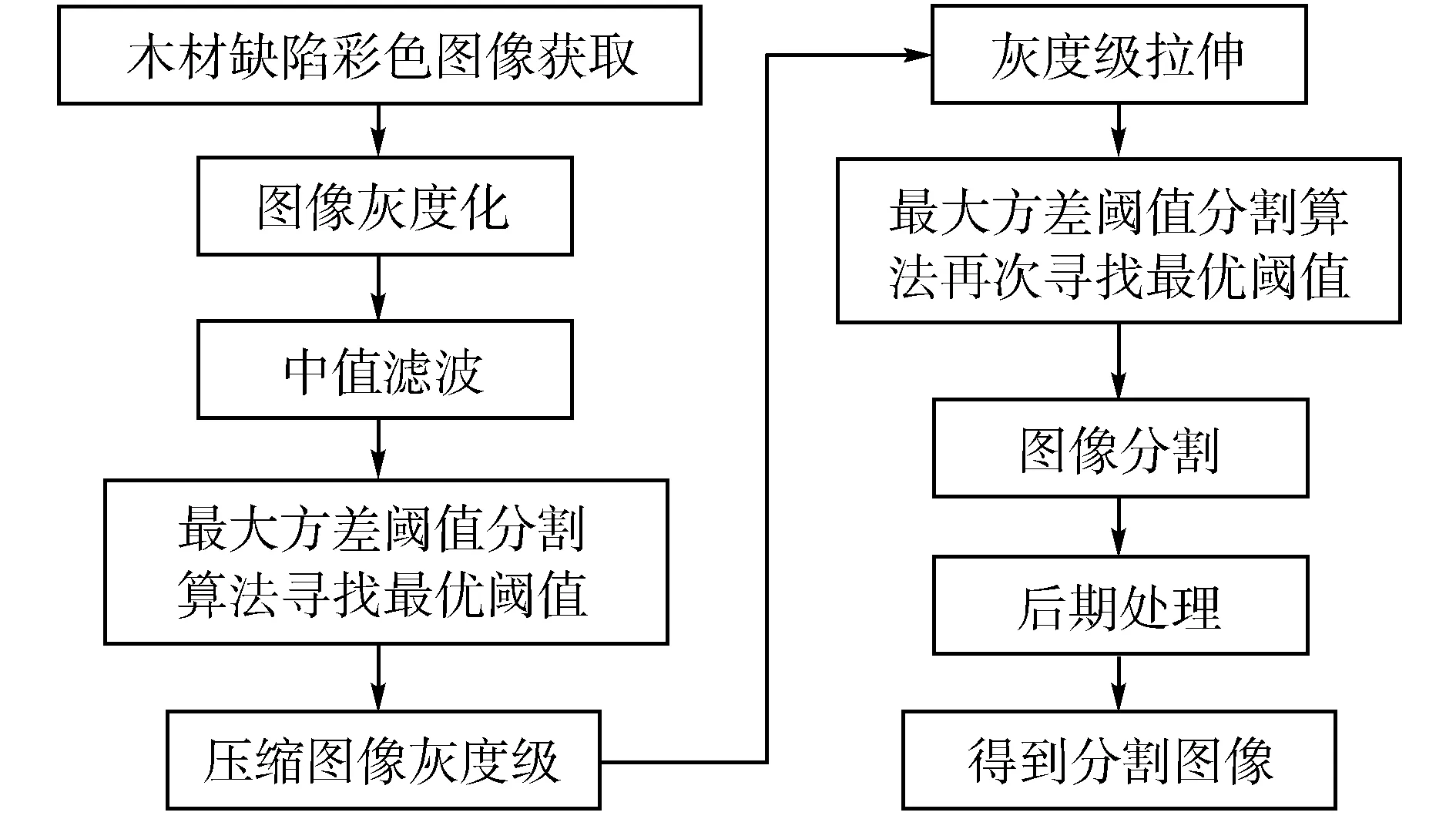
图4 改进的木材缺陷分割算法流程图

(18)

Xmax=[T*1.5]。

(19)

Xmin=[T/2]。

(20)

其中，Xmax是图像灰度级压缩后的最大灰度值；Xmin是图像灰度级压缩后的最小灰度值；G(i，j)代表原图像中位于第i行、第j列的像素点的灰度值，[]表示取整。显然，灰度级压缩后的图像的某些灰度值会消失。

为了增强目标和背景区域的对比度，还要对灰度级压缩后的图像进行灰度级拉伸。此处选用线性拉伸方法，即原图像的灰度级和拉伸后的图像灰度级呈线性关系。设原图像灰度级用变量X表示，相应的拉伸后的图像灰度级用变量Y表示，则：

(21)

由此可得，灰度级拉伸后的图像的灰度级为：

(22)

其中，Ymax为灰度级拉伸变换之后期望的图像的灰度最大值，Ymin为灰度级拉伸变换之后期望的图像的最小灰度值。

令：

则：

Y=aX+b。

(23)

显然，这是一条以a为变换斜率，以b为基数得线性变换函数，当a>1时，图像的灰度级得到拉伸。运用公式23可以对图像灰度级进行合理调整。

灰度级拉伸之后，图像中目标和背景区域的对比度得到大大增强，再次运用最大方差阈值分割算法对图像进行分割，然后对分割图像进一步处理，主要是去除小块区域，填充分割图像的孔洞，则可得到木材缺陷的分割图像。选取虫眼、活节和死节三种典型的木材缺陷对算法进行实验，其具体分割效果对比如图5所示：

6 结 论

通过几种木材缺陷的阈值分割算法的比较，得出最大方差阈值分割算法分割效果较好，但是在某些情况下也有一定的局限性，尤其对于目标和背景区域对比度不明显时，其分割效果的准确性大大降低。为解决这一问题，通过对原始图像灰度级的压缩和拉伸，使得图像的目标和背景区域的对比度得到增强，进而使得最大方差阈值分割算法的分割效果得到很大改善。但是，这些都只是基于图像灰度直方图基础上的，是一维阈值分割算法的应用研究。

图5 改进算法对3种木材缺陷的分割效果对比

【参 考 文 献】

[1] 马大国，马 岩，姜新波，等.基于LS-SVM的木材表面缺陷网格化检测[J].林业科技开发，2012，26(6)：73-76.

[2] 汪丹平，唐 勇.基于直方图的迭代式自动阈值分割技术研究[J].软件导刊，2011，10(8)：32-33.

[3] 吴东洋，叶 宁，徐 波，等.基于Otsu算法的木材缺陷图像分割[J].计算机与数字工程，2012，40(10)：116-118.

[4] 吕行军，韩宪忠，王克俭，等.基于最大方差阈值法的火车票图像二值化处理[J].计算机应用与软件，2012，29(7)：249-253.

[5] 王克奇，马晓明，白雪冰.基于分形理论和数学形态学的木材表面缺陷识别的图像处理[J].森林工程，2013，29(2)：48-52.

[6] 李 瑱，夏良正，顾宗悫.一种新的二维最大熵图像阈值分割算法[J].南京航空航天大学学报，1994(26)：151-157.