基于ANSYS的圆锯片模态分析和振动分析

张绍群，焦广泽

(东北林业大学 机电工程学院，哈尔滨 150040)

圆锯片的振动是指锯片上某一点在他的平衡位置偏移一定的距离或者扭转一定角度的往复运动。由于锯齿与木材的碰撞，锯轴、圆锯片质量不平衡等原因，圆锯片的振动是不可避免的。圆锯片对这些因素的响应决定了锯片的振动模态。激振力有周期变化的，也可能是随机的[1]。剧烈振动直接影响了锯切质量和锯片寿命，也严重影响生产安全和生产效率，同时锯片剧烈振动产生的噪声也严重影响现场工作人员的身心健康[2]。绝大多数情况下圆锯片的振动都是由多个单一振动模态复合而成，且各个模态都有相应的表现，因此圆锯片呈现较为复杂的震动形式，不会表现出特定的模态，不能确定其固有频率和振型。然而只有处于共振时，圆锯片才表现为单一振动模态。并且，每个单独的振动模态都有其相应的固有频率和确定节圆数节径数的振型。

木工圆锯机是一种危险有害机械，圆锯片的工作状态是一个高速旋转的危险状态，因此在设计锯机和锯片时，必须了解锯片的固有频率特性。对锯片振动进行控制，提高圆锯的固有频率，提高切削稳定性，可以节省大量的加工资源。在所有提高圆锯片动态稳定[3]

本文采用ANSYS12.0有限元软件作为主要分析手段，有针对性地进行了硬质合金圆锯片的模态分析，为圆锯机及圆锯片的设计避免出现共振、疲劳及其他受迫振动提供技术依据，并为圆锯片的模态检测提供一种实用的方法。

1 有限元振动分析模型

锯片的振动主要由沿半径方向的径向震动、沿转轴方向的横向震动以及环绕径向的扭转震动复合而成，其中轴向振动最为关键，集中了锯片振动的主要能量[2]且横向振动的功率主要集中在低频范围内(<2 kHz)[4]。因此应当着重研究分析锯片的低阶振动频率和振型。锯片的前后倾角会激发锯片的横向振动。有拨料齿的锯片也可能会激起并增加锯片的横向振动[5]，因此本文重点分析计算锯片的低频横向振动。

圆锯片是一个形状复杂的薄板状的结构，实际分析可忽略锯齿复杂的几何形状，将圆锯片看作是一个中间固定、外沿自由的等厚薄壁圆盘，如图1所示。D为锯片的半径，d为锯片夹盘的半径，h为锯片厚度。

图1 圆锯片的振动模型

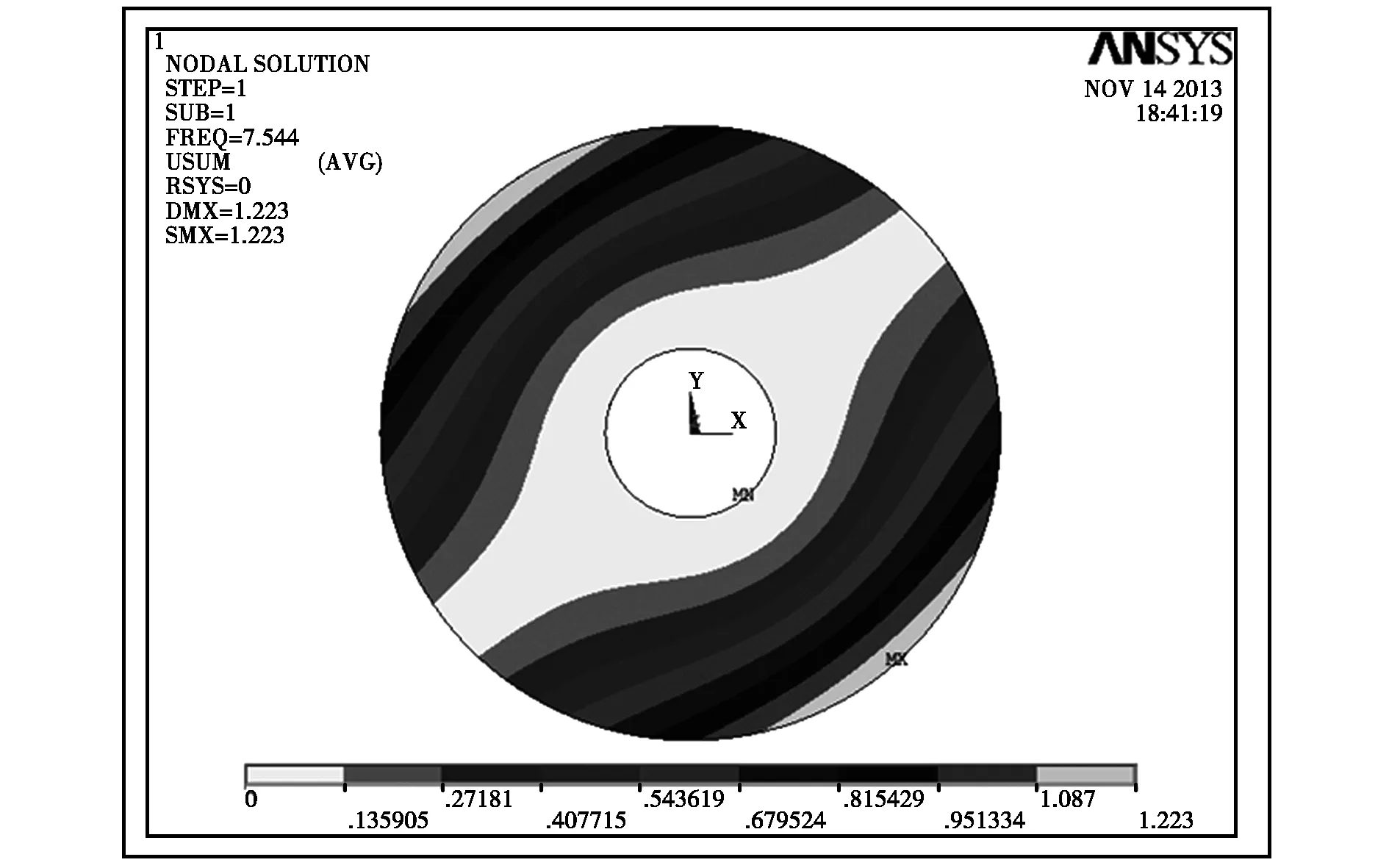
图2 圆锯片的位移矢量和图

实际生产中，锯片由夹盘夹紧固定在锯机的转轴上，锯片与转轴的联结为固定约束。由于夹盘质量较大，厚度较大，具有较好的刚度，不会产生变形，最终将圆锯片的有限元振动分析模型简化成中间固支约束，外边自由的圆环板模型。

2 圆锯片主要参数

本文中所用圆锯片直径D为405 m，中心孔距齿尖的距离为202.5 mm，齿高为10mm，在计算时以200 mm为计算半径，齿高与锯片直径相比很小，因此锯齿可忽略不计[6]，其外形尺寸参数及材料参数见表1。

表1 圆锯片的外形尺寸参数和材料参数

3 模态分析

根据图1给出的硬质合金圆锯片的振动模型，在ANSYS12.0(APDL)软件中，采用She1163壳单元，建立硬质合金圆锯片有限元物理模型，得到1 830个节点，1 749个单元。

进入Read Results，选择第一个模态，查看对应的Displacement vector sum位移矢量和图(如图2所示)，由图中给出固有频率为7.544频率，位移矢量和1.223，振型为m=0，n=1。其他各个模态的固有频率，位移矢量和及振型由表2列出。

表2 圆锯片的模态、频率、位移矢量和

根据表2得到的数据可以得到的固有频率和位移矢量和的关系，可得到位移矢量和随固有频率的变化图。如图3和图4所示。

图3 圆锯片的位移矢量和与固有频率的关系

图4 圆锯片的位移矢量和与节径数的关系

4 进行振动试验，检验震动的固有频率

利用DH5922动态信号测试分析系统和DH1031扫频信号发生器，DH103压电式加速度传感器，进行谐响应分析，在DH1031扫频信号发生器的控制面板设置需要的信号参数：信号类型：线性扫频；起始频率：0 Hz；截止频率：150 Hz；扫速：1 Hz/s，电压2 600 mv。如图5所示。

图5 实验装置简图

图6 圆锯片未共振时的加速度

4.1 未共振时的图像及分析

进入实验时，激振器的频率从1～7变化时，加速度曲线如图6所示。

由图6可知，到圆锯片的固有频率未和激振频率耦合时，圆锯片的振动表现为多种震动状态，其中任意一种震动都未单独表选出来。利用积分/微分选项，如图7所示，对加速度进行2次积分，得到位移图如图8所示。

由图8可以看到，由于没有出现共振，此时的位移矢量和(振幅)变化幅度较小。

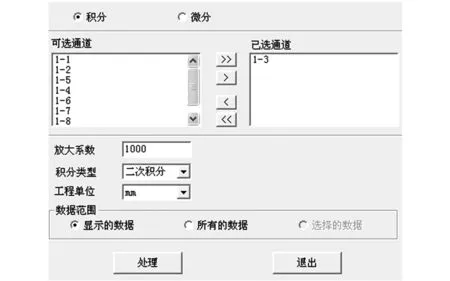
图7 加速度积分成位移的设置

图8 圆锯片未共振时的位移

4.2 7Hz共振时的图像及分析

进入第一个模态时，激振力的作用是在不破坏r=1阶振型的情况下，克服r=1阶阻尼来维持结构系统的r=1阶纯模态振动[6]。此时，圆锯振动的加速度随着国有频率和激振频率的耦合而突然变大，此时，激振频率为7Hz，与ANSYS软件得到的结果相似。由图9和图10可知，此时圆锯片处于共振状态，但激振频率较低，共振并未得到大幅加强。

图9 圆锯片第一次耦合时的加速度

图10 圆锯片第一次耦合是的位移图

4.3 71HZ共振时的图像及分析

当激振频率为71Hz时，圆锯片加速度的变化幅度较大，此时的加速度最大值达到549.3m/s，并伴有明显的噪声，可以明显的判定此时处于共振状态。如图11所示。

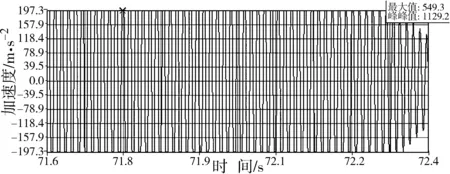
图11 激振频率为71Hz时圆锯片的加速度

图12 激振频率为71Hz时圆锯片的及位移

通过积分后的位移图可知，此时的位移(振幅)和初始时刻的位移相比变化较大。如图12所示。

4.4 152HZ共振时的图像及分析

当激振频率为152Hz时，圆锯片加速度的变化幅度较大，此时的加速度最大值达到964.4 m/s，并伴有明显的噪声，位移变化较大，可以明显的判定此时处于共振状态。如图13和图14所示。

4.5 软件分析与实验结果的比较

ANSYS计算得出的固有频率，和DH5922动态信号测试分析系统得出的固有频率的比较。如图15所示。

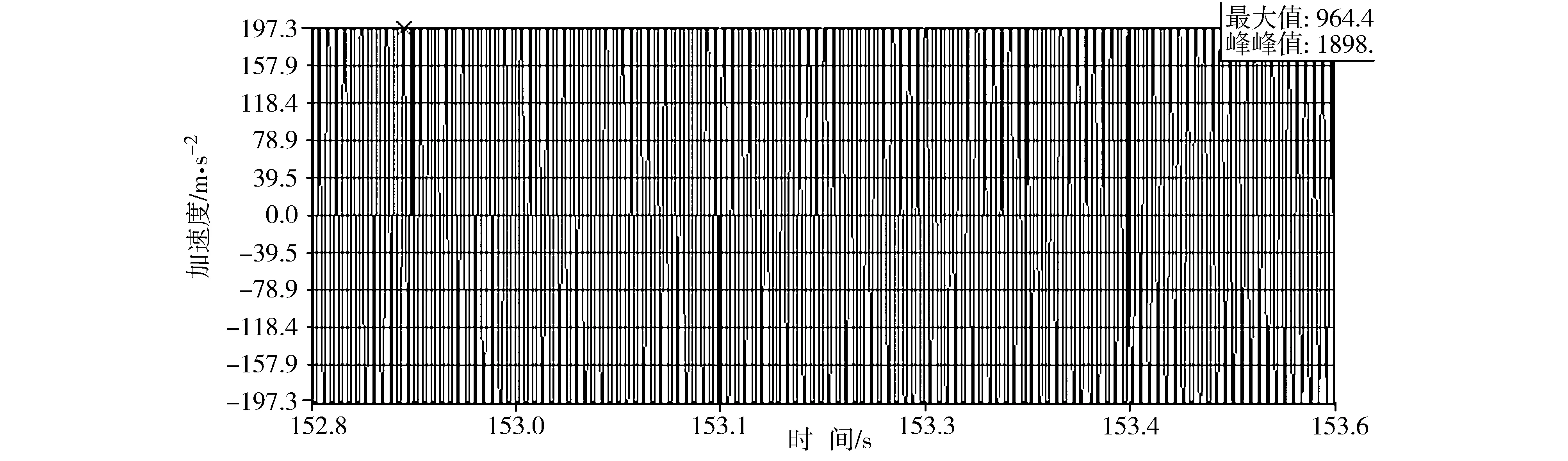
图13 激振频率为152Hz时圆锯片的加速度

图14 激振频率为152Hz时圆锯片的位移

图15 ANSYS分析结果和实验对比图

由图可知，ANSYS软件计算得出的结果较为密集，而通过DH5922动态信号测试分析系统得出的结果较为稀疏，但两者的大致趋势一致。

5 结 论

(1)利用ANSYS软件可以快速得到相应的模态，确定相应的振型、振幅和固有频率。

(2)圆锯片的固有频率在同一节圆时，节径数增加，固有频率也随之增加，位移也随之增加，既振幅随节径数的增加而增加。

(3)圆锯片处于共振(纯模态)时，其边缘处的位移矢量和与模态有关，即和节圆数和节径数有关，当节圆数m=0时，圆锯边缘处的位移矢量和随节径数增加而增加，且呈线性增加。当节圆数m=1时，圆锯边缘处的移矢量和随节径数增加而减小，也呈线性减小。当节径数n=0时，不论节圆数m=0或节圆数m=1，其位移矢量和大小相等。

(4)通过利用DH5922动态信号测试分析系统，可以确定相应的固有频率，其固有频率与ANSYS软件得到的结果接近。通过利用DH5922动态信号测试分析系统可以测出对圆锯片危害最大的频率，如40、71和150 Hz。大约为2倍递增的规律。

【参 考 文 献】

[1] 李 黎，习宝田，杨永福.圆锯片振动、动态稳定性及其控制技术的研究——圆锯片的振动分析和动态稳定性[J].木工机床，2002(2)：5-10.

[2] 姜阳春，王 正.基于ANSYS的木工圆锯片有限元模态分析[J].木工机床，2005(4)：9-12.

[3] 张东梅，尚春民，乔彦峰.圆锯片振动频率的控制方法[J].噪声与振动控制，2005(4)：52-54.

[4] 邹家祥.圆锯片的动态特性[J].北京科技大学学报，1994，16(S1)：94-97.

[5] 杨红义，潘 静，杨红梅.基于ANSYS圆锯片动态性能研究[J].林业机械与木工设备，2010，38(4)：24-26.

[6] 臧 勇，李同进.圆锯片的有限元模态分析[J].重型机械，2002(1)：49-52.