基于几何模型系统动态结构图的梅森增益公式用法研究
韩俊青
(德州职业技术学院 电气系,山东 德州 253034)
0 引言
研究控制系统就必须建立系统的数学模型,经典控制理论中常用的数学模型有时域模型—微分方程,复域模型—传递函数[1],频域模型—频率特性[2].但最常用的数学模型是传递函数,频率特性只是传递函数的特殊形式.如何利用动态结构图求系统传递函数来定量分析系统的动静态性能是分析问题的关键[3].但在实际应用过程中如何能全面深刻的理解这一公式的含义,并能灵活地运用它,还不够完善,本文基于几何模型系统动态结构图,通过分析其特点即回路是否相关联研究这一问题.
1 梅森公式求解系统传递函数
求传递函数可利用动态结构图的等效变换,即分支点和比较点的前移和后移等,太费时费力,梅森公式与以上方法比较有它的先进性,它可不用繁琐的变换一步可求得系统传递函数[4],梅森公式如下:
(1)
式中各项含义如下:Δ为特征式,Δ=1-∑li+∑lilj-∑liljlz+…
其中∑li为各回路传递函数之和,即指回路前向通道与反馈通道传递函数的乘积;∑lilj为两两互不接触回路传递函数的乘积之和;∑liljlz为所有三个互不接触回路传递函数的乘积之和;pk为第k条前向通道的传递函数,n为系统中前向通道的条数;Δk为特征式对第k条前向通道的余子式,它既可以通过从Δ中除去与第k条前向通道接触的所有回路传递函数项得到.理论上梅森公式可以说是神通广大,但实际应用中用起来,稍一疏忽,容易将前向通道数、反馈回路数及余子式判断错.
2 梅森公式在相关联系统中的简化
区分系统是否“相关联”,若为“相关联多回路系统”,此时梅森公式可直接简化为:
其他情况直接应用梅森增益公式(1),“相关联”即所有的回路和前向通道必须共用一个“环节”或“一段信号线”,如图1、图2共用一个环节的相关多回路系统.

图1 共用一个环节的只有一条前向通道的相关多回路系统
以上系统有一条前向通道,三个回路,它们共用了一环节G3(s)比较明显,所以为相关多回路系统直接用公式(2)求得
(3)
各回路之前若为负反馈为“+”若为正反馈为“-”.
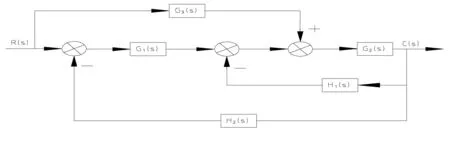
图2 共用一个环节两条前向通道的相关多回路系统
以上系统有两条前向通道,两个回路,它们共用了一环节G2(s),所以为相关联系统,直接应用公式(2)求得
P1=G1(s)G2(s))
(4)
P2=G3(s)G2(s)
(5)
(6)
见图3、图4共用一段信号线的相关多回路系统

图3 共用一段信号线的相关多回路系统
图3中第一个分支点之前和第三个比较点之后的一段为相关联多回路系统,也可以直接应用公式(2)求解
P1=G1(s)G2(s)G3(s)
(7)
P2=G1(s)G4(s)
(8)
(9)
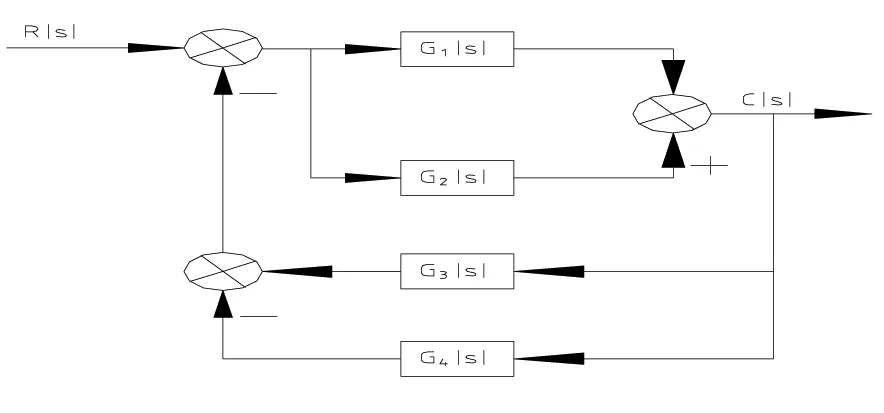
图4 共用一段信号线不规则的相关多回路系统
图4中两条前向通道和四个个反馈环节即回路共用了最后一个比较点和最后一个分支点之间的一段信号线,因此系统为相关联多回路系统,也可以应用公式(2)求解
P1=G1(s))
(10)
P2=G2(s)
(11)
(12)
但若把图3中G2(s)环节前的分支点移到它前面比较点的前方即G1(s)环节后方,见图5.此时此系统的两条前向通道和各个反馈回路既没有共用的环节,也没有共用的信号线,因此此系统就不相关联了,只能利用梅森公式(1)求解.
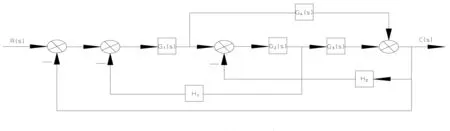
图5 非相关联多回路系统
∑li=G1(s)G2(s)H1(s)+G2(s)G3(s)H2(s)+G1(s)G2(s)G3(s)+G1(s)G4(s)
(13)
∑lilj=0,∑liljlz=0
(14)
Δ=1+G1(s)G2(s)H1(s)+G2(s)G3(s)H2(s)+G1(s)G2(s)G3(s)+G1(s)G4(s)
(15)
P1=G1(s)G2(s)G3(s),Δ1=1
(16)
P2=G1(s)G4(s),Δ2=1+G2(s)G3(s)H2(s)
(17)
(18)
再如图6看似各回路相关联,仔细观察分析各回路及前向通道既没有共用的环节也没有共用的信号线,为非相关联多回路系统,只能用梅森公式(1)求解.
∑li=G1(s)G2(s)+G1(s)H(s)+G3(s)H(s)
(19)
∑lilj=0,∑liljlz=0
(20)
Δ=1+G1(s)G2(s)+G1(s)H(s)+G3(s)H(s)
(21)
P1=G1(s)G2(s),Δ1=1+G3(s)H(s)
(22)
(23)
3 结论
本文就系统的相关联性进行分析,根据图中具体情况应用梅森公式(1)(2)分析求解,可以得到应用梅森公式(2)进行求解具有很多优点.
[1]孙振川.基于s函数的异步电动机在两相静止坐标系下的仿真建模[J].枣庄学院学报,2012,29(5):82-84.
[2]韩俊青.基于系统开环频率特性曲线的奈奎斯特判据用法研究[J].枣庄学院学报,2014,31(2):44-46.
[3]黄坚.自动控制原理及应用[M].北京:高等教育出版社,2005.
[4]熊新民.自动控制原理与系统[M].北京:电子工业出版社,2003.

