高斯测度的再生核Hilbert空间与Sobolev空间的关系

胡修炎

(枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

经典框架下单位球面，区间[-1,1]和单纯形上函数逼近已经发展的较为全面[1-3]，如何将经典框架下的逼近结果应用到平均框架下就成为一个很重要的问题.Jackob Creutzig在2002年的文章[4-6]中得到了经典的与平均Kolmogorov宽度之间的关系，给平均框架下的逼近研究带来了很大的方便.由于这个关系式中需要用到再生核Hilbert空间，所以，在研究Sobolev空间在平均框架下的逼近时，就需要先建立起具有高斯测度的Sobolev空间与其再生核Hilbert空间的关系，才能利用经典的Kolmogorov宽度的结果.研究平均框架下函数逼近的文章都用到了高斯测度的再生核Hilbert空间与的Sobolev空间的关系，但是文章中都没有给出这种关系式的理论证明.本文就将给出单位球体上具有高斯测度的加权Sobolev空间及该测度的再生核Hilbert空间的关系式的证明方法，并且由于再生核Hilbert空间的光滑指标与权函数、维数无关，所以该证明可以推广到单位球面，区间[-1,1]，单纯形上具有高斯测度的加权及非加权的Sobolev空间中，具有普遍意义.

1 预备知识

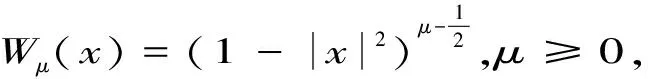
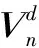
(1.1)

其中

(1.2)

表示L2,μ中的内积.

对于给定的r>0，定义分布意义下f的r阶导数为

(1.3)

于是，Bd上的加权Sobolev空间定义为

(1.4)

其中的内积为

[f,g]r=[f(r),g(r)]，

(1.5)

λl=(l(l+2μ+d-1))-s/2，(s>d)，

(1.6)

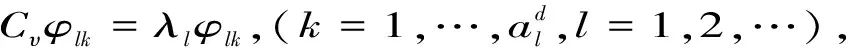
(1.7)

2 主要结果及证明

记X是可分的Banach空间，X*表示X上的所有连续线性泛函，γ是X上的中心高斯测度，则诱导测度γ°f-1是R上的高斯测度.用LP(X,dγ)表示X上的γ可测泛函，其有限拟范数为

(2.1)

则X*可以嵌入LP(X,dγ).那么测度γ的再生核Hilbert空间(又称为Cameron-Martin空间)定义为

(2.2)

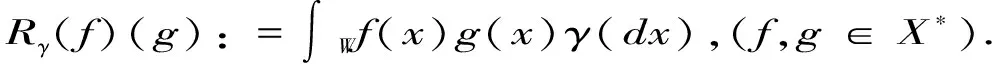
(2.3)

我们先来证明一个重要的引理.

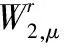
(2.4)

证明简记I=n(n+d+2μ-1)，根据(1.6)-(1.8)及(1.3)有

所以根据柯西不等式以及(2.2)有

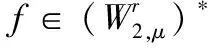
得(2.4).引理证毕.

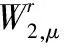
(2.6)

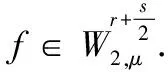
(2.7)

即f∈H(υ).综合(2.6)(2.7)得(2.5)式.定理证毕.

3 结论

再生核Hilbert空间的光滑指标与权函数、维数无关，由此该证明方法同样适用于球面，单纯形上的非加权的和加权的Sobolev空间，所以具有普遍意义.

[1]Brown G, Dai F, Sun Y S. Kolmogorov width of classes of smooth fuctions on the sphere Sd-1[J]. J Complexity, 2002,18:1001-1023.

[2]Brown G, Dai F. Approximation of smooth functions on compact two-point homogeneous spaces [J]. J Funct Anal, 2005,220:401-423.

[3]Dai F. Kolmogorov and linear widths of weighted Besov classes[J]. J Math Anal Appl, 2006,315: 711-724.

[4]Wang H P, Huang H W. Widths of weighted Sobolev classes on the ball[J]. J Approx Theory, 2008,154(2):126-139.

[5]Huang H W, Wang K Y. On the widths of Sobolev's classes[J]. J Complexity, 2011,27(2): 201-220.

[6]张艳伟. 具有高斯测度的Sobolev空间上的算子逼近[J].枣庄学院学报,2009,(5):73-77.