一类加权的Jackson型不等式与Marcinkiewicz-Zygmund型不等式

翟学博

(枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

经典的Jackson型不等式和Marcinkiewicz-Zygmund(下面简称M-Z)型不等式广泛的应用于函数逼近理论和调和分析中.近几年来，这类不等式在加权和不加权的情形下都有了一些结果.2005年，徐源证明了单位球面、单位球体和单纯形上的加权Jackson型不等式.2006年，戴峰得到了单位球面、单位球体上的M-Z不等式.而对于区间[-1,1]上加权Sobolev空间中的Jackson型不等式和M-Z型不等式都没有给出明确的证明，本文就对此做了研究，并给出了证明过程.

1 预备知识及主要结果

考虑[-1,1]上的权函数wα,β(x):=(1-x)α(1+x)β,α,β>-1/2，用Lp,α,β(1≤p<∞)表示具有有限范数

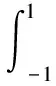
的可测函数构成的空间，当p=∞时，用连续函数空间C[-1,1]代替L∞,α,β.对于f∈Lp(wα,β)，令

En(f)p,α,β:=inf{‖f-P‖p,α,β:P∈Πn}

(1.1)

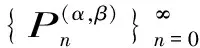
(1.2)

hn(α,β)～n-1只依赖于α,β.于是对于任意的f∈L2,α,β，都有

(1.3)

接下来给出加权Sobolev空间的定义.

对于给定的r>0，定义分布意义下f的r阶分数次导算子为

(1.4)

于是，[-1,1]上的加权Sobolev空间定义为

(1.5)

我们的主要结果叙述如下：

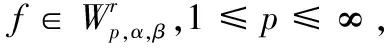
En(f)p,α,β≼n-r‖(-Dα,β)r/2f‖p,α,β.

(1.6)

此不等式为Jackson型不等式，下面的不等式即是M-Z型不等式.

定理2 对于1≤p≤∞，f∈Πn，我们有

(1.7)

2 主要结果的证明

首先介绍一些定义和记号.记

(2.1)

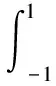
(2.2)

则[2]对于g∈Πn，有Vn(g)=g，对于任意的f∈Lp,α,β，(1≤p≤∞)，有Vn(f)∈Π2n，且有

‖Vn(f)‖p,α,β≼‖f‖p,α,β，‖f-Vn(f)‖p,α,β≼En(f)p,α,β.

(2.3)

其中En(f)p,α,β的定义由(1.1)给出.

我们先来证明Jackson型不等式.

定理1的证明 由(C,n)的Cesàro平均的定义[3]以及(1.2)(1.3)有

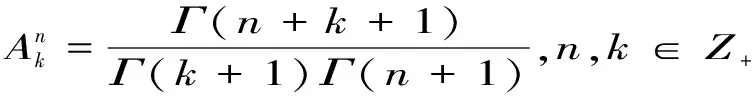
取[4]μk=(k(k+α+β+1))-r/2，τk=(μk)-1，令

(2.4)

使用Abel变换n+1次，得

(2.5)

由于Δn+1μk≼k-n-1-r，根据[5]中论断1.1和(2.4)(2.5)可得

≼n-r‖(-Dα,β)r/2f‖p,α,β.

(1.6)得证.定理1证毕.

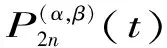
引理[1]对于n≥1，求积公式

对于4n-1次多项式精确成立.

定理2的证明 在[6]中的命题1中令p=1得

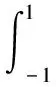
再由(2.2)(2.3)得

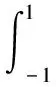
(2.6)

其中在第二个不等式中应用了Hölder不等式.

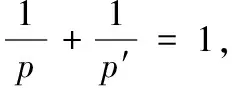
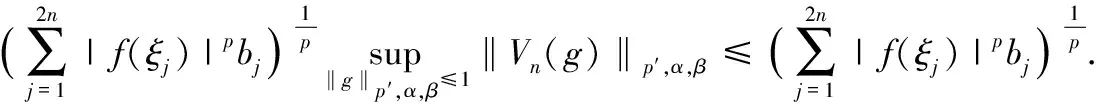
(2.7)

综合(2.6)(2.7)得(1.7)式成立.定理2证毕.

[1]Szego G. Orthogonal Polynomials[M]. Amer Math Soc Colloq, 1975,23(4).

[2]Kyriazis G, Petrushev P, Xu Y. Jacobi decomposition of weighted Triebel-Lizorkin and Besov spaces[J]. Studia Math, 2008,186: 161-202.

[3]Dunkl C F, Xu Y. Orthogonal polynomials of several variables[M]. Cambridge Univ Press, 2001.

[4]Kamzolov A I. Approximation of smooth functions on the sphere Snby the Fourier method[J]. Mathematical Notes, 1982,31:428-432.

[5]Dai F, Ditzian Z. Cesàro Summability and Marchaud inequality[J]. Constr Approx, 2007,25:73-88.

[6]Petrushev P, Xu Y. Localized polynomial frames on the interval with Jacobi weights[J]. J Four Anal Appl, 2005,11:557-575.