基于学习和全变分最小化的超分辨图像复原

李丽荣

(天津大学理学院数学系，天津300072)

图像的分辨率表征了图像详细信息的丰富程度.提高图像的分辨率是图像处理领域以及计算机视觉领域研究的重要课题.图像超分辨率复原(super resolution image reconstruction，SISR)就是提高图像分辨率的方法之一.超分辨率图像复原突破了传统的依靠硬件设备性能的提高来得到高分辨率图像的限制，依靠软件技术获取所需的高分辨率图像，降低了成像成本，具有更广阔的发展空间和研究价值.

基于学习的超分辨率图像复原方法是近年来研究的热点，这是一种利用机器学习训练给定的图像集，并寻找测试图像与预先建立的训练集之间的先验关系来得到高分辨率的图像的方法.基于学习的超分辨率复原方法在先验知识较少、高频信息缺失较多的情况下能够获得分辨率较高的图像，因此在超分辨率图像复原时具有很大的优势.Freeman等[1]提出的基于示例学习的 Markov模型，利用Markov网络对高低分辨率的空间关系进行建模;Chang等[2]提出的基于邻域嵌入的学习方法，提出高低分辨率图像具有相同局部几何结构的流形.这些方法都得到较好的复原效果，但要求训练样本和测试样本数目多，对噪声敏感.为了得到更好的超分辨率复原图像，Yang等[3]利用机器学习和压缩感知的理论提出了基于稀疏表示(Sparse coding super－resolution，SCSR)的图像超分辨率复原方法.

Rudin等[4]在 1992年提出了全变分(Total Variation，TV)模型用于图像去噪，取得了较好地效果.这种方法建立在泛函分析和微分几何的数学模型基础上，保留了图像的边缘信息.随着超分辨率图像复原的发展，TV最小化逐渐被引入到图像复原中，文献[5]采用全变分离散表示模型复原超分辨率图像.

本文将全变分最小化(TV)正则项引入到基于学习的图像复原模型中，并采用交替迭代法求解.另外与文献[3]的超完备字典训练方法不同，本文应用K－SVD方法训练字典.最后结合非局部均值法和迭代反投影法对得到的复原图像进一步处理，提高图像的分辨率.

1 基于稀疏表示的超分辨率复原模型

对于一幅低分辨率图像Y，如果用表示其对应的高分辨率图像，则超分辨率图像复原的观测模型为:

其中:S表示下采样矩阵，H表示点扩散函数或衍射极限引起的模糊矩阵，ν表示噪声.

根据基于示例的思想，把图像分成大小相同的图像块，称为一个patch，在不考虑模糊矩阵和噪声的情况下，高分辨率图像块x∈Rn与相应的低分辨率图像块y∈Rm之间的关系可以表示为:

超分辨率图像复原即在已知低分辨率图像块y的情况下恢复高分辨率图像块x，这是一个欠定问题，不能直接求解.文献[3]通过学习的方法求解该问题，利用图像库中的图片联合训练高分辨率字典Dh和低分辨率字典Dl，对于低分辨率图像块y，若可以通过低分辨率字典Dl稀疏表示为α，则相应的高分辨率块x可以通过高分辨率字典以及α得到.而求图像块y的稀疏表示α可以表示为以下问题:

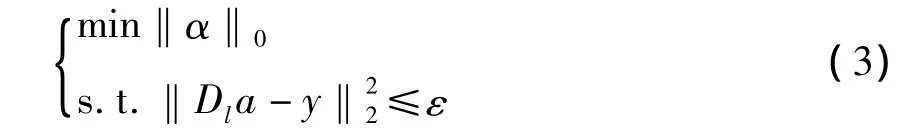
在α充分稀疏的情况下，问题(3)可以松弛为以下问题求解:

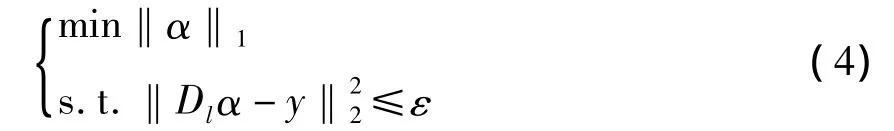
根据拉格朗日乘子法，上式可以表示为:

假设公式(5)的最优解为α*，则高分辨率图像块x可以通过x=Dhα*重建得到.

2 TV正则化模型

2.1 全变分的概念

n ×n 图像块 x，xi，j，表示位于第 i行第 j列的像素值，则x的全变分则表示为:

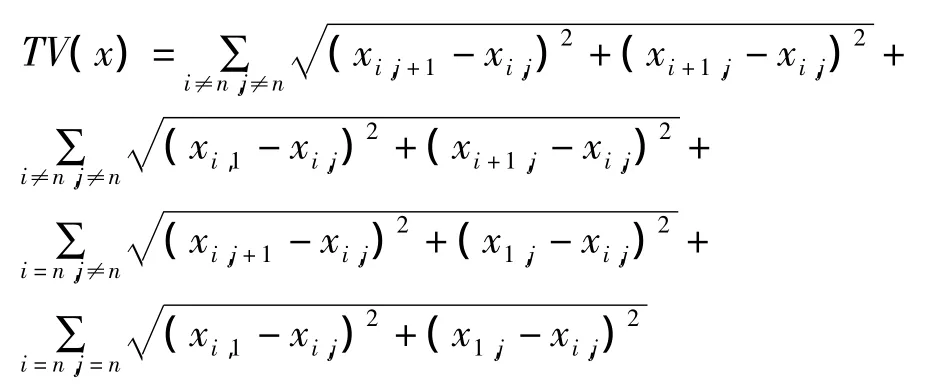
2.2 超分辨率图像复原TV模型

由于图像像素之间很强的相关性，图像的梯度在大部分区域是接近于零的，因此图像的梯度空间也是稀疏的.TV最小化适用于图像的重构，可以更好的保留图像边缘，考虑把全变分正则项加入到SCSR方法中，并把向量化，得到基于学习的全变分超分辨率复原模型:

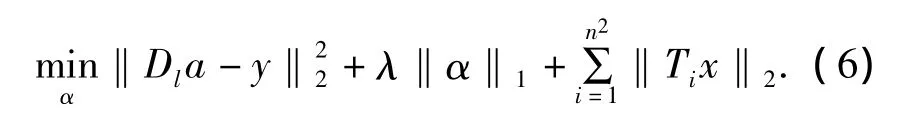
引入辅助变量 w=[w1;…;wN]，N=n2，wi∈R2，使得wi=Tix，为了保证这个公式成立，我们加入惩罚项，从而有以下模型:

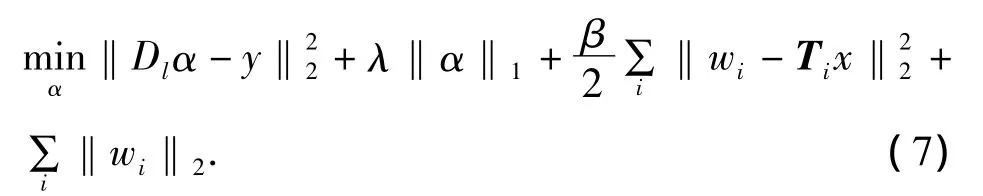
对于上述模型采用交替迭代法[6]求解，把问题(7)简化为以下两个便于求解的子问题:

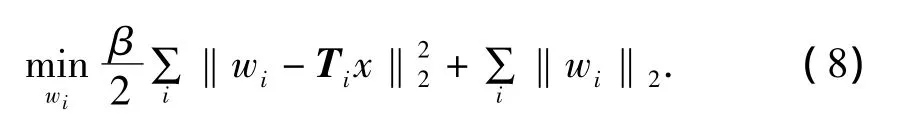
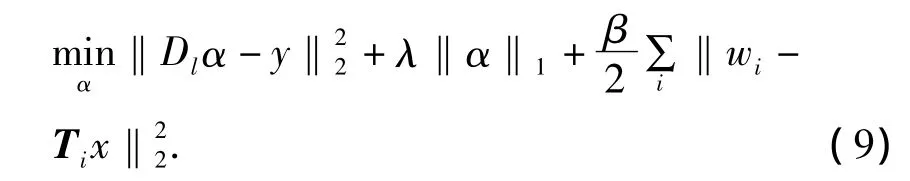
令 ωj=(w1(j);…;wN(j))，j=1，2，由 T(1)，T(2)的定义，式(9)中

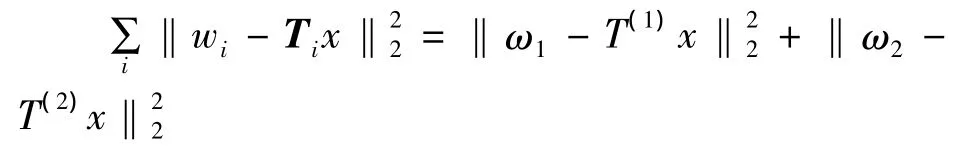
因此，子问题(9)可以写为:

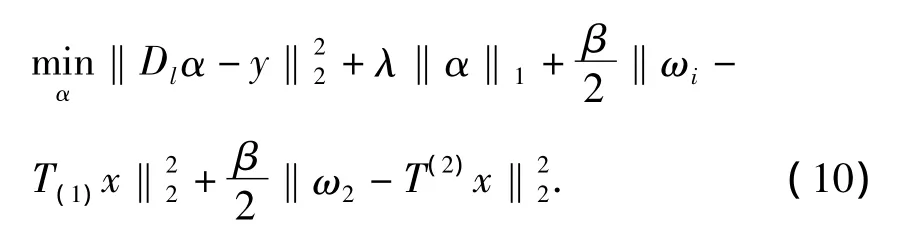
式(10)可以表示为:

可以简化为最优化问题:

则原始目标函数可以简化为下述两个子问题，然后采用交替迭代法求解:

首先求解式(9)，在这个子问题中，wi是自变量，该问题有封闭公式解，即:

并且设定0·(0/0)=0.对于问题(12)，这是一个优化问题，可以直接采用梯度下降法求解.

关于迭代终止条件的设定，本文采用常用的方法，即当迭代次数满足预先设定的值或者复原图像之间的残差满足设定的阈值δ的时候迭代终止.

为了得到复原效果较好的图像，通过上述方法复原图像后，本文利用非局部均值算法[7]和迭代反投影算法[3]对得到的高分辨率图像进一步处理.

2.3 算法流程

通过上面的分析，本文整个算法流程总结如下:

输入:低分辨率图像Y，图像放大倍数af;

步骤1:选取高分辨率图像块和低分辨率图像块，应用K－SVD方法联合训练字典，得到高分辨率字典Dh和低分辨率字典Dl;

步骤2:通过插值得到初始高分辨率图像块x(0);

步骤3:重复以下迭代，直到满足终止条件

1)根据公式(8)求解得到wi;

2)固定wi，根据公式(12)解优化问题求得α;

3)令 x=Dhα，β =2β，返回 3.1.

步骤4:复原超分辨率图像X0，用非局部均值法和梯度下降法对X0进行后处理.输出:高分辨率图像X*.

3 仿真结果及分析

本文的仿真实验在Matlab R2013b版本上运行，电脑配置为Windows7/64bit系统，4G内存.本算法使用与文献[3]相同的训练图像集采用KSVD方法[8]训练字典，算法中图像放大倍数af为2，测试低分辨率图像大小为128×128，所以复原的高分辨率图像大小为256×256，复原过程中采用的图像块大小为5×5.

为了证明本文算法的有效性，将其与插值算法和SCSR算法的实验结果进行对比，以峰值信噪比(PSNR)来评价复原效果，由图1可以看出，本文算法在视觉效果上比另外两种算法更好，且PSNR值有所提高.

4 结语

本文采用K－SVD方法训练字典，提出在基于字典学习的超分辨率图像复原模型中引入全变分正则项，通过变量替换把复原模型转化为等价的优化问题并求解.本文算法在峰值信噪比和视觉效果上比SCSR算法都有所提高.由于采用交替迭代法求解，需要在迭代过程中不断增加惩罚参数β的取值，容易造成迭代过程的数值不稳定性，如何克服这个缺点是进一步研究的内容.

图1 本文算法与其他算法复原效果比较

[1]FREEMAN W T，JONES T R，PASZTOR E C.Example based super－ resolution[J].IEEE Computer Graphics and Applications，2002，22(2)，56 －65.

[2]CHANG H，YEUNG D Y，XIONG Y.Super－ resolution through neighbor embedding[C]//IEEE Computer Society Conference on ComputerVision and Pattern Recognition.Washington.DC，USA，2004:275－282.

[3]YANG J C，WRIGHT J，HUANG T，et al.Image super－ resolution via sparse representation[J].IEEE Transaction on Image Processing，2010，19(11):2861－2873.

[4]RUDIN L，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms[J].Physica D，1992(60):259－268.

[5]YANG J，ZHANG Y，YIN W.A Fast TVL1－L2 Minimization Algorithm for gorithm for signal reconstruction from partial Fourier data[J].IEEE Journal of Special Topics Signal Process，2008，4(2):288－297.

[6]WANG Y，YANG J，YIN W，et al.A new alternating minimization algorithm for total variation image reconstruction[J].SIAM Journal on Imaging Sciences，2008，1(3):248－272.

[7]BUADES A，COLL B，MOREL J M.A non－local algorithm for image denoising[C]//Proc.IEEE COMSOC Conf.Computer Vis.Pattern Recognit.2005:60 －65.

[8]AHARON M，ELAD M，BRUCKSTEIN K S.An algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Trans.On Signal Processing.2006，54(11):4311 － 4322.