基于Copula的债务抵押债券定价

王 珺，梁冯珍

(天津大学理学院，天津300072)

债务抵押债券(CDO)是近年发展最迅速最具创新力的金融产品之一，是资产证券化技术应用于信用风险管理上的金融衍生产品.当资产的违约之间存在相关性时，单个资产发生违约可能导致其他资产同时发生违约，从而造成投资人巨大损失.因此，CDO定价中的关键在于如何准确地评估相关资产违约概率以及衡量彼此之间的违约相关性.

在CDO定价模型中，最常用的方法是基于单因子Copula方法.CDO的市场标准定价方法为Li[1]中提出的单因子 Gaussian Copula 模型.由于Gaussian Copula无法描述尾部相关性，从而在CDO定价过程中产生相关性微笑(correlation smile)现象.为了消除这种现象，学者们提出了很多新的方法，其中包括 t-Copula[2]，double t-Copula[3]，Clayton Copula[4]and normal inverse Gaussian Copula[5].Frey，McNeil and Nyfeler[6]首次将 Copula 应用于行业模型中.Hofert and Scherer[7]应用嵌套Archimedean Copula来描述相关资产之间的违约相关结构.更多的细节可以参考文献[8-9].

本文运用时点结构选择改变时点.由于Copula函数的选择对CDO定价存在决定性的影响，应用AIC准则确定最合适的Copula函数来描述债务人之间的违约相关结构.在此基础上应用Monte Carlo算法模拟出各相关资产的违约时间，通过CDO定价模型为各系列进行定价.

1 债务抵押债券

1.1 债务抵押债券结构

债务抵押债券是将资产池中的资产按照风险和收益特征分类后，由一个特殊目的机构(SPV)发行的不同级别风险和收益的证券.我们称这样的结构为分债(tranche)，投资者可以根据其风险偏好来进行投资.文献[10]对CDO产品进行了更详细的介绍.

在CDO交易中，当相关资产的损失超过设定的值或损失达到债务池(collateral pool)的某一水平时，CDO的支付发生.每一分债由临界点(attachment points)和分离点(detachment points)构成.临界点定义了资产池中特定分债开始经历损失之前的整个损失水平，分离点定义了资产池中特定分债经历了完全本金损失的整个损失水平，其中分债的规模由分离点和临界点之差决定，它定义了特定分债的最大损失程度.表1给出了一个CDO的结构，其中股权分债(equity or residual tranche)位于分债机制的最底层，其分离点是10%即基础资产的第一个10%的信用损失被股权分债吸收.当信用损失达到12%时，由夹层分债(mezzanine tranche)吸收剩下的2%损失.类似地，当信用损失在20%和35%之间时损失由高级分债(senior tranche)吸收.而资产组合损失超过35%的部分将全部由超高级分债(supper supper senior tranche)承担.

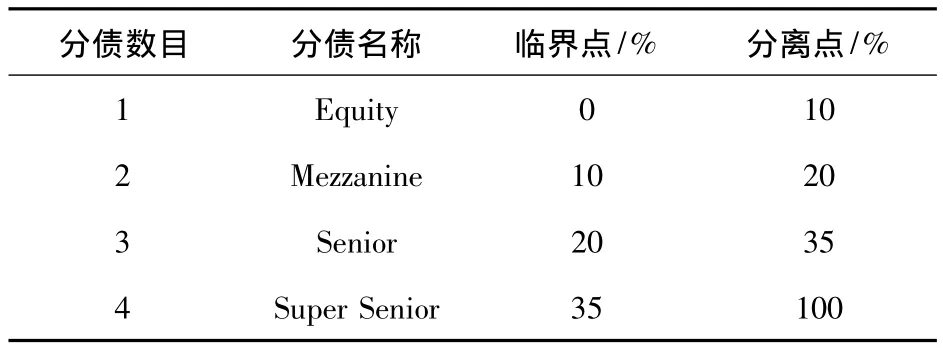
表1 CDO分债结构

1.2 CDO 的计算

考虑[t0，T]内分债个数为J相关资产为d的CDO，在t时刻资产池的累积损失为

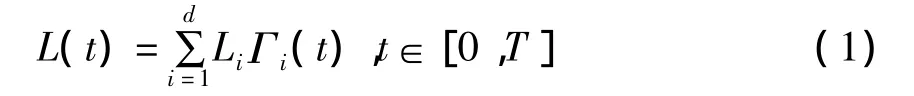
其中:Li=(1-Ri)Vi为资产i的违约损失，Vi为其名义总值，1-Ri为违约损失指标，Ri称为回收率，Γi(t)=1(τi≤t)，i=1，…，d，为违约指示函数即当违约变量 τi≤t时，资产 i在时刻 t，t∈[t0，T]发生违约.

考虑CDO的一个分债，其临界点和分离点分别为A和B，其中定义 M(t)为给定分债的累积损失，则

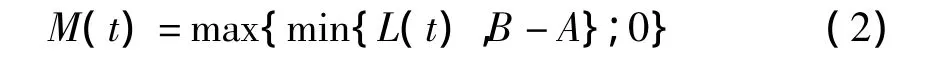
在CDO交易中，一方(保护买方)持有的一些资产可能会由于发生某种信用事件(credit event)遭受损失.为了寻求保护转移信用风险，该交易者向愿意承担风险信用保护的另一方(保护卖方)在合同规定的期限内定期支付一笔固定的费用.保护卖方在接受费用的同时，承诺在合同的期限内，当相应的信用事件发生时，向保护买方赔付一定的金额.此时，我们称保护买方支付金额的现值为保险支付(PL)，称违约发生时保护卖方赔付金额的现值为违约支付(DL).此时，违约支付(DL)可以写成

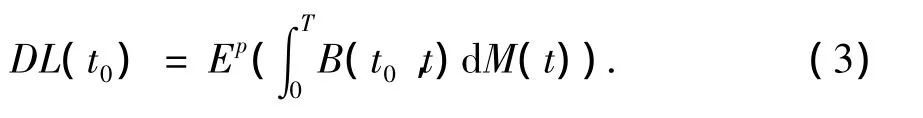
在CDO交易中，交易双方提前约定支付时间，通常为半年一次，直到M(t)=B-A或者合约到期.因为违约随时可能发生，此处我们假设违约发生在两个违约日期之间，则保险支付(PL)表示为

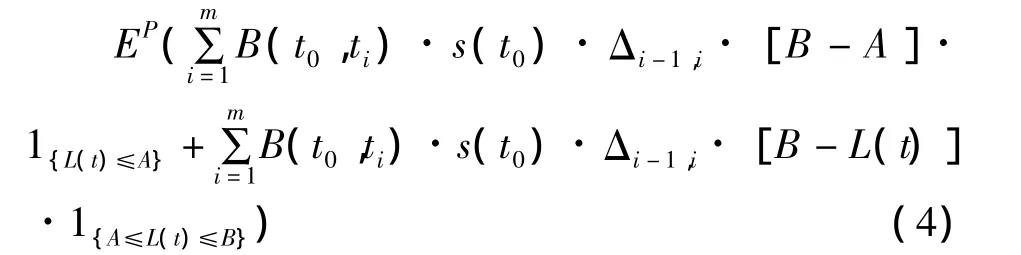
其中:B-A为给定分债所承担的最大损失，m为总支付日期，ti为违约支付日期，Δi-1，i为连续违约支付日的间隔(通常为半年)，B(t0，t)为折现因子，s(t0)为给定分债的定价.假设保险支付是即时的，则保险支付可以写成

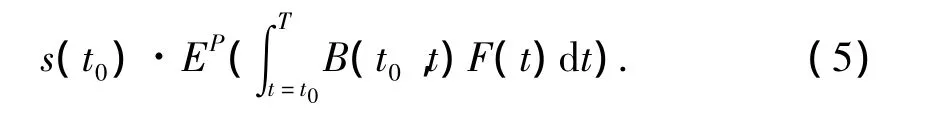
其中:F(t)=min{max{B-L(t)，0}，B-A}.

在无套利情况下，违约支付和保险支付金额相等即

那么，可以求得CDO的公平利差(fair spread)为:

2 CDO定价模型

在CDO定价中最流行的是因子Copula模型.但是选择何种Copula函数来描述违约相关结构是CDO定价的核心.本文应用AIC准则选择最合适的Copula，同时应用时点改变模型来描述违约相关结构的动态性.

2.1 Copula模型

本节给出几种常见Copula的定义以及AIC准则的计算方法.更多详细内容请见参考文献[9]和[11].

定义1 [多元Gaussian Copula(MGC)]

令R为diag(R)=(1，1，…1)T的对称正则矩阵，ΦR为协方差阵为R的标准多元正态分布函数.我们定义MGC为

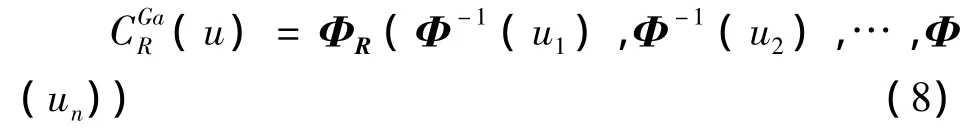
其中Φ-1为标准正态分布函数的逆函数.

定义2[多元Student t copula(MTC)]

令R 为diag(R)=(1，1，…，1)T的对称正则矩阵，tR，υ为自由度为 υ，协方差为 R的标准多元Student t分布函数.我们定义MTC为

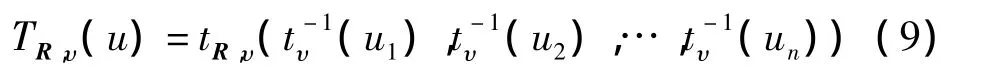
定义 3[多元 Archimedean copula]

令 Archimedean生成元 ψ:[0，∞]→[0，1]，在[0，inf{t:ψ(t)=0}]上严格递减且满足 ψ(∞):=，我们定义这样的函数集为若对任意 t∈[0，∞)，ψ(t)＞0，这样的 ψ∈Ψ 称为严格生成元，则Archimedean CopulaC表示为:

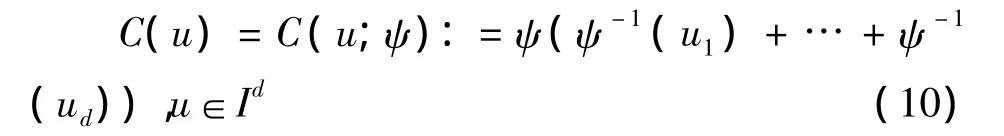
其中 ψ∈Ψ 且满足 ψ-1:[0，1]→[0，∞]，ψ-1(0):=inf{t:ψ(t)=0}.

定义 4[多元 hierarchical Archimedean copula(HAC)]

当Archimedean copula中的变量被Archimedean copula代替时，我们称这样的C为嵌套Archimedean copula.当d=2即为式(10)，当 d≥3时嵌套Archimedean copula形式为:

这样的称为全嵌套Archimedean copula，否则称为偏嵌套Archimedean copula.

从定义4中可以看出，Archimedean copula是嵌套Archimedean copula的特例.由于嵌套Archimedean copula结构中存在分层结构，我们也称嵌套Archimedean copula为分层Archimedean copula(HAC).

定义 5[Akaike’s信息准则(AIC)]

Akaike’s信息准则的定义如下:

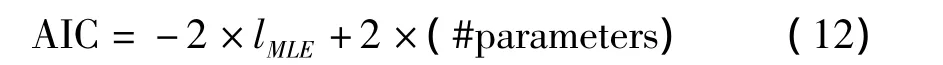
其中lMLE为所估计模型的对数似然函数值，#parameters为所求统计模型的参数个数.

在应用AIC标准来选择统计模型时，我们选择AIC值最小的备选模型.因此应用AIC标准选择模型，不仅考虑到拟合优度的问题，同时还考虑了参数数目问题.

2.2 时点改变模型

由于市场条件是随着时间而改变的，此时违约时间的相关性同样随着时间而改变.经过检验，各金融资产的日对数收益回报显示出异方差性.为了描述资产日对数收益回报的性质，我们提出ARCH模型即

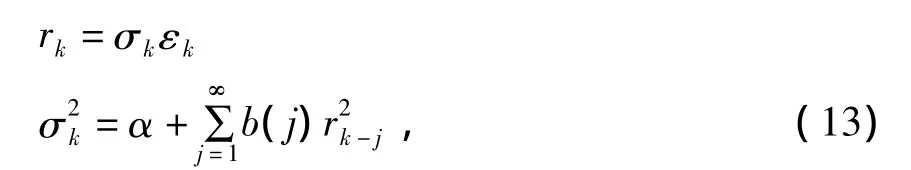
其中:εk为 i.i.d.均值为零，方差为 1 的随机变量，α和b(j)为非负常数.下一步应用改变时点结构估计改变时点k*.应用CUSUM方法对改变时点k*进行估计，记为，此时的估计值为

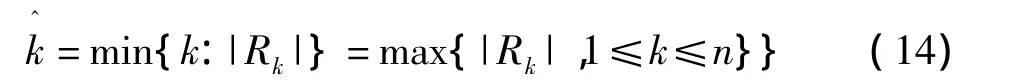
其中:Rk

多元时点改变模型可以参考文献[12-13].当我们确定改变时点k*之后，整个观测期被分为若干阶段，下面求不同的阶段违约时间的相关结构.

2.3 违约，联合违约和Copula函数

设资产i的违约时间 τi，i=1，…，d的分布函数为Fi，则在时间[0，t]发生违约概率为 pi(t)=P{τi≤t}=Fi(t).假定违约实现的过程为Poisson过程，其强度函数为λi(t)，则资产i的无条件违约概率为

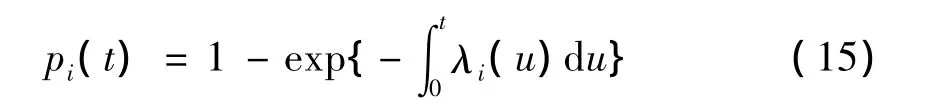
此时，对应的生存概率为

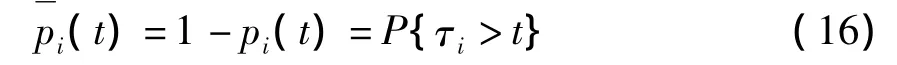
更多的细节问题可以参考 Schönbucher[14].在本文中，假设Poisson过程的强度为常数，则从式(17)中即可计算出资产i的违约时间为τi=-lnUi/λi.

CDO定价模型的核心之处在于如何描述各资产违约时间的相关性.应用变量为触发变量U1，…，Ud的 Copula函数，违约时间 τ1，…，τd的联合分布函数可用U1，…，Ud的联合分布函数表示为

因此，应用 AIC准则，我们从 MCG，MCT，Gumbel，Clayton，Frank，hierarchical Gumbel and hierarchical Clayton Copula中确定最适合数据的Copula.当Copula类型确定之后，即可运用Monte Carlo模拟方法计算出CDO的公平差价.

3 CDO定价模拟

从万科，保利，中国银行，中国工商银行，平安和人民财产保险六个公司三个行业中构建一个模拟的CDO产品，并应用Copula函数对其进行定价.这六支股票数据包含从2007年3月1号到2011年12月30号共1 113组，来源于 http://www.ccerdata.com.假设每个资产的本金为 100，000，000美元，CDO的到期日为一年，市场无风险利率为3%，Possion过程的强度为0.125.

首先从式(15)中估计出单个违约变量τ1，i=1，…，6的分布函数.

然后从式(14)中确定改变时点，此时求出的改变时点为2007年9月25日，2008年8月24日即整个观测期被分为三个阶段.在每个阶段内，应用AIC准则选择最适合的Copula函数来拟合样本数据.经过检验发现，Archimedean Copula族中的Gumbel，Clayton和Frank Copula均不是最适合的.由于不同行业的相关性和同一行业的相关性均不相同，在第一阶段已证明出嵌套Gumbel Copula是最适合的，此时的嵌套Gumbel Copula形式为:

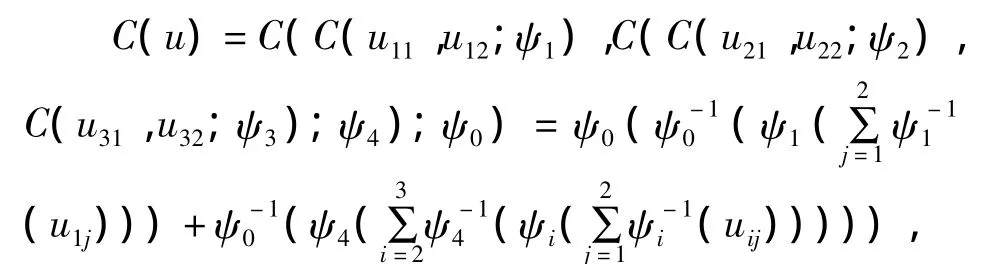
其中 ψi，i=0，1，2，3，4 为 Gumbel Copula 生成元.其中ψ1描述了万科和保利的相关结构，ψ2描述了中国银行和工商银行的相关结构，ψ3描述了平安和人民财产保险之间的相关结构，ψ4描述了银行业和保险行业之间的相关结构，ψ0描述了房地产、银行和保险三个行业之间的相关结构.在第二阶段我们已证明Gaussian Copula是最适合的，此时求出的P-值为0.1454，且检验出对于我们备选的多个Copula所有P-值均小于0.05.在第三阶段求出的最适合的Copula为自由度为5的Student t Copula.当确定出每一阶段最适合的Copula函数之后，应用最大似然估计方法(ML)估计对应模型中的参数.表2给出相应的参数估计值，其中第二阶段和第三阶段的参数值代表这六个公司的线性相关系数.

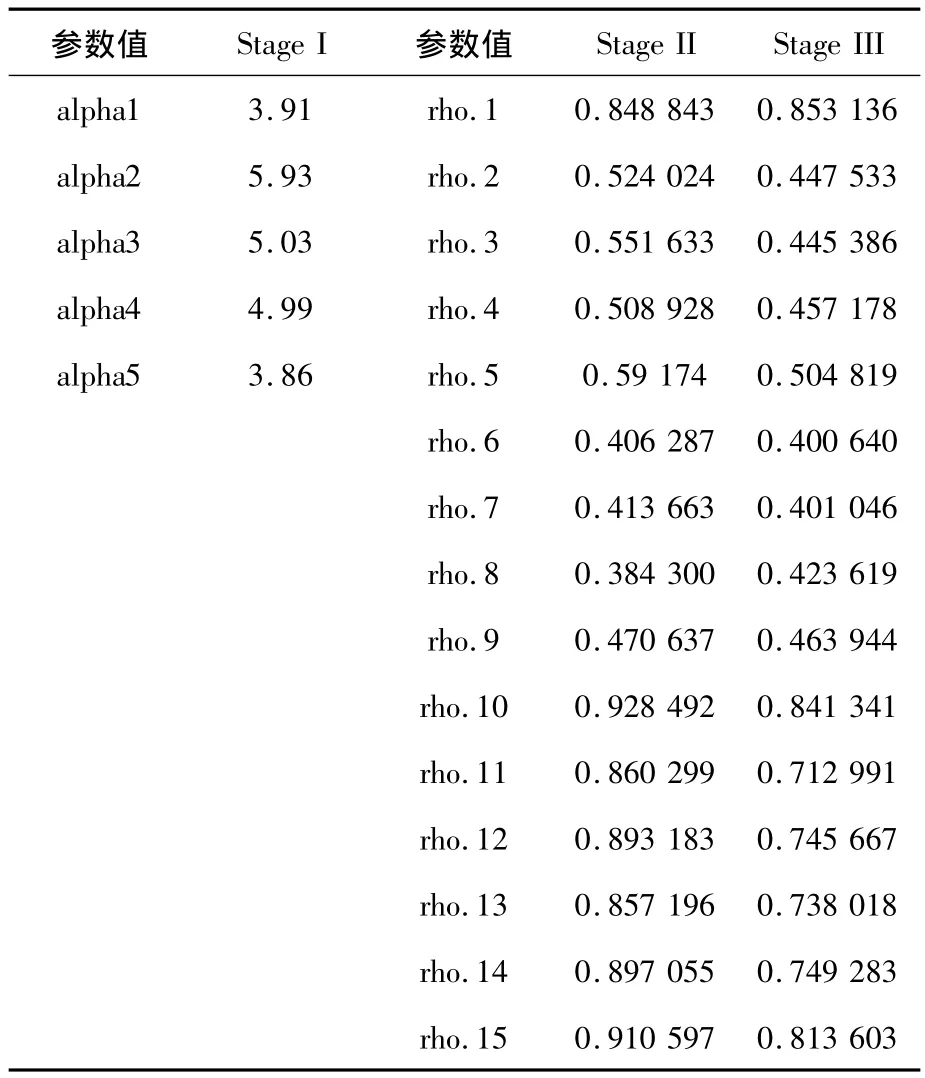
表2 参数估计

从表2中可以看到，银行和保险行业间的相关性很强，而房地产行业的相关性相对弱一些.应用Monte Carlo模拟产生10 000个服从所求Copula函数的触发变量 U1，…，U6即(U1，…，U6)～ C.应用模拟产生的数据，我们从式(3)和式(5)中分别计算出违约支付(DL)和保险支付(PL).当计算出保险支付和违约支付后，即可从式(7)中计算出CDO的定价s(t0).公式中的期望值通过对10 000组模拟数据求平均值来求解，在表3中给出求解出的CDO在各个阶段的定价和期望损失.

从表3中看出，CDO在三个阶段的定价和期望损失是不同的，尤其在资产分债和夹层分债的定价区别更是明显.和第一阶段相比，第二阶段和第三阶段在各阶段的定价区别不大.在现实中，债务池的名义总值很大，公平利差的一点点改变都会产生很大的区别和损失.从这点来看，在不同阶段内相关结构不同，从而求出的公平利差也不同.所以当我们确定了改变时点之后选择何种Copula函数来描述违约相关结构，对CDO的定价至关重要.

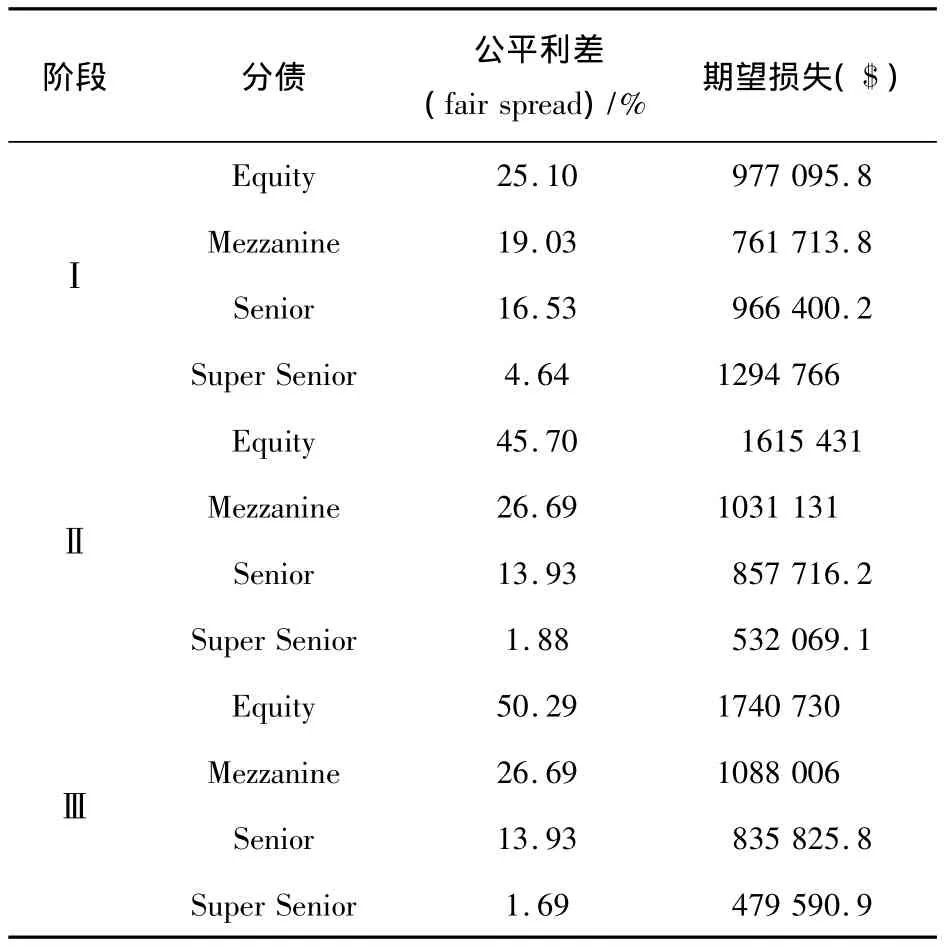
表3 期望损失和公平利差

4 结语

CDO是较为复杂的金融产品，应用Copula函数对其定价的核心在于如何选择最合适的Copula函数.在本文中应用改变时点结构在一定程度上描述资产违约动态相关性.且选择AIC准则确定Copula函数不仅考虑到拟合优度，同时考虑了参数个数对模型的影响.但是限于市场数据和计算效率，数值计算部分仅是一种简化情况，对市场上的CDO产品定价有待进一步分析.

[1]LI D X.On default correlation:a copula function approach[J].The Journal of Fixed Income，2000，9(4):43-54.

[2]SCHLOEGL L，O’KANE D.A note on the large homogeneous portfolio approximation with the student t copula[J].Finance and Stochastics，2005，9(4):577-584.

[3]HULL J，WHITE A.Valuation of a CDO and an nth to default CDS without Monte Carlo simulation[J].Journal of Derivatives，2004，12(2):8-23.

[4]FRIEND A，ROGGE E.Correlation at First Sight[J].Economic Notes，2005，34(2):155-183.

[5]KALEMANOVA A，SCHMID B，WERNER R.The normal inverse Gaussian distribution for synthetic CDO pricing[J].Journal of Derivatives，2007，14(3):80-93.

[6]FREY R，MCNEIL A，NYFELER M.Copulas and credit models[J].Risk，2001，14(10):111-114.

[7]HOFERT M，SCHERER M.CDO pricing with nested Archimedean copulas[J].Quantitative Finance，2011，5(11):775-787.

[8]OKHRIN O，OKHRIN Y，SCHMID W.On the structure and estimation of hierarchical Archimedean copulas[J].Journal of E-conometrics，2013，173(2):189-204.

[9]HOFERT M.Sampling nested archimedean copulas with applications to CDO Pricing[M].Germany:Suedwestdeutscher Verlag für Hochschulschriften，2010.

[10]BLUHM C，OVERBECK L.Structured credit portfolio analysis，baskets and CDOs[M].USA:Chapman and Hall/CRC，2006.

[11]NELSEN R B.An introduction to copulas[M].New York:Springer-Verlag，1999.

[12]CSÖRGÖ M，HORVATH L.Limit theorems in change-point analysis[M].New York:Wiley，1997.

[13]KOKOSZKA P，LEIPUS R.Change-point estimation in ARCH models[J].Bernoulli，2000，6(3):513-539.

[14]SCHÖNBUCHER P.Credit derivatives pricing models:model，pricing and implementation[M].USA:John Wiley＆ Sons，2003.