一种新型PBG-CPW传输线

李晓明,郭文刚

(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

0 引 言

近年来,共面波导得到了日益广泛的关注[1-3]。光子带隙(PBG)[4-5]则因禁带特性为学者所重视并引入微波电路。传统CPW设计参数只有导带宽度地间隙,而PBG可加工在介质中,为设计带来更高灵活性。作者在文献[6]中提到一种部分介质共面波导(PS CPW)传输线,并对其各项特性进行讨论。PBG-CPW可看作由多段CPW和PS CPW首尾相连而成,在一定条件下可等效为均匀传输线。

1 CPW和PBG结构

CPW是1969年由Wen[1]提出的一种微波平面传输线,以易于串并联、低损耗、低色散、集成度高等优点得到广泛研究,已应用于各种微波集成电路。1987年Yablonovitch和John分别独立提出光子晶体概念[4-5]。光子晶体是指一种介质在另一种介质中周期排列组成的晶体结构,能产生PBG。在PBG材料中,带隙内的电磁波被完全禁止传播,此特性具有极大理论价值和应用前景。近年来,PBG被引入微波领域,迅速成为研究热点[7-8],应用于各种微波平面传输线,如微带[9-10]、CPW[9-11]等。PBG往往加工于微带或CPW的金属地平面[9-10],直接在介质上设计PBG结构的研究则很少[11]。

2 新型的PBG-CPW结构

新型PBG-CPW,如图1所示,其中(a)为俯视图,(b)和(c)则是不同位置截面图,分别对应CPW和PS CPW[4]两种传输线。在传统CPW两槽介质中周期打尺寸为p1×p2的矩形孔,即可形成PBG-CPW。

PBG-CPW可用于设计的尺寸包括CPW的尺寸wc、ws,PBG单元的尺寸p1、p2和重复周期S.wg为地的实际宽度,一般取较大值,通常不作为设计参数。PBG-CPW比CPW多三个设计参数,比PS CPW多两个设计参数,其设计灵活性的提高不言而喻。

3 PBG-CPW的特性分析

如前所述,PBG-CPW为非均匀传输线,包含PBG结构,可预见具有禁带特性,因此无法用传统均匀传输线的分析方式进行研究。然而这种结构的重复周期S通常较小,所对应的禁带频率往往远高于使用频段,故可考虑在一定条件下对这种传输线的模型进行简化。

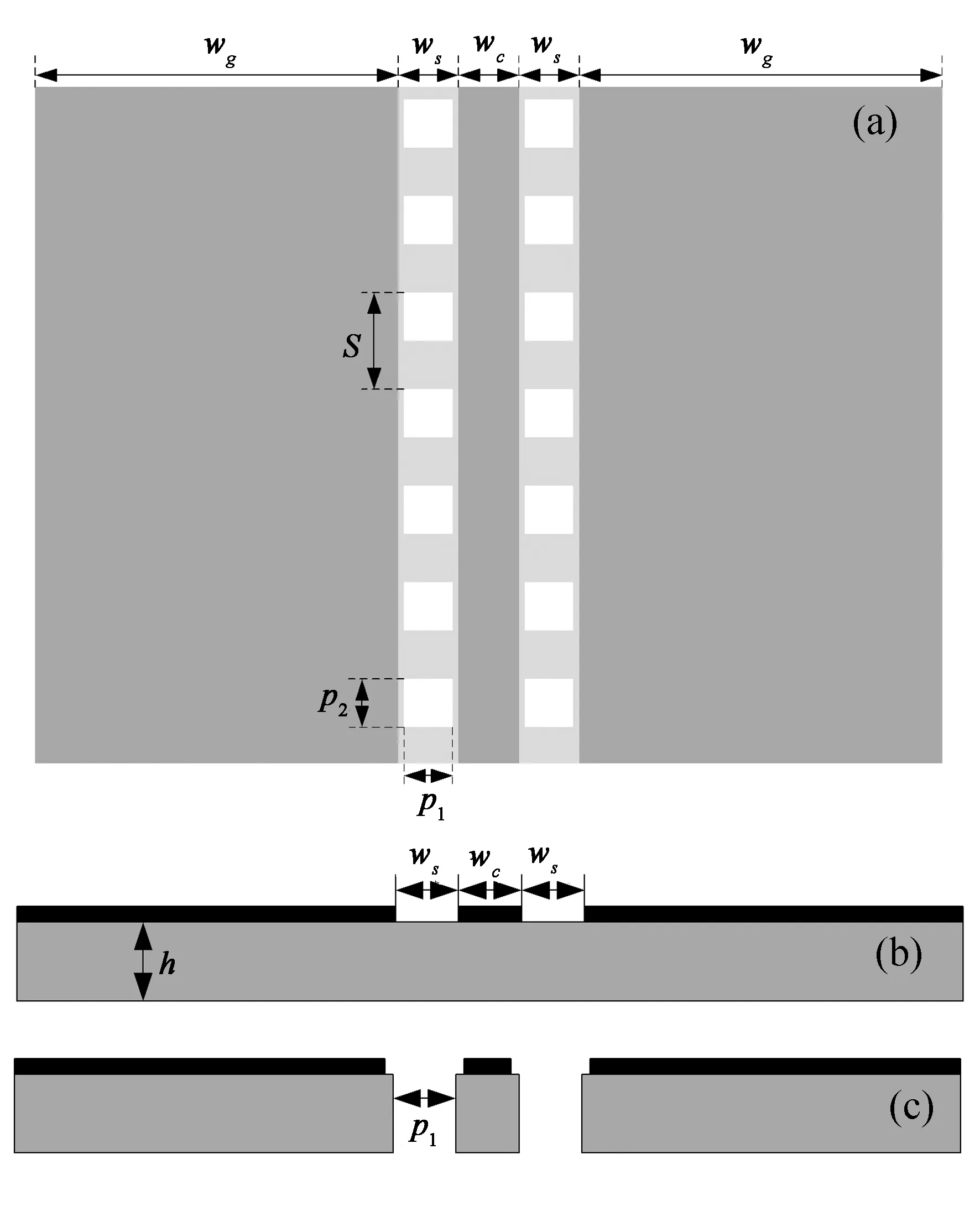
图1 所提出的PBG-CPW示意图 (a)平面图; (b)CPW截面图;(c)PS CPW截面图

3.1 PBG-CPW相速和有效介电常数分析

如果只考虑传输线中电磁波的相位传播速度而暂不考虑反射,且电磁波在CPW中的相速为υp1,而在截面如图1(c)的PS CPW中为υp2,那么可定义PBG-CPW传输线中的平均相速为

υpa=s/(p2/υp2+(s-p2)/υp1).

(1)

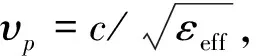
(2)

若给定参数CPW的有效介电常数为εeff1,则由文献[4]知,PS CPW的有效介电常数εeff2只与p1有关,可定义εeff2=m2(p1)εeff1,其中关于p1的函数m(p1)可简写为m,其表达式为m=(εeff2/εeff2)1/2,令n=p2/S,则式(2)可改写为vpa=vp1/(1-n(1-m)).易知,m的取值范围为(1/εeff1,)],n的范围是[0,1],传统CPW可看作m=1或n=0时的特例。相应地,整个传输线的有效介电常数可写为

εeffa=[1-n(1-m)]2εeff1.

(3)

3.2 PBG-CPW的阻抗分析

组成PBG-CPW的两种传输线CPW、PS CPW特性阻抗不同[4],分界面上必然存在复杂的反射。传输线有效介电常数和特性阻抗的计算公式分别如(4)、(5)所示。其中,C为单位长度上的分布电容,C(εr=1)对应于将介质用空气填充的单位长度电容。

εeff=C(εr)/C(εr=1).

(4)

(5)

对图1(b)与(c)所示截面而言,改用空气填充后,其单位电容,即C(εr=1)完全相同,因而这两种截面的特性阻抗应如式(6)所示关系

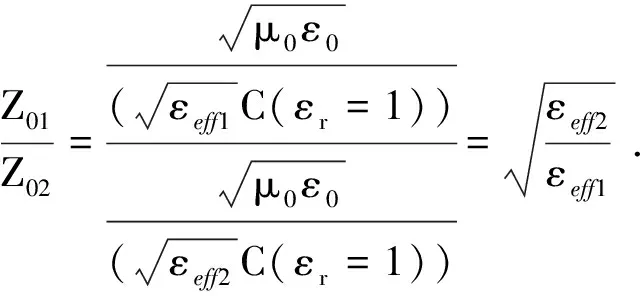
(6)

代入前文引入的m,有Z02=Z01/m.可见PS CPW的特性阻抗只与m有关,如欲控制CPW及PS CPW分界面上的反射,则应合理选择m的大小;而由前文知,相速υpa与m和填充系数n都有关,控制更为灵活。如果结构的重复长度S足够小,则可定义传输线的平均阻抗Z0a如式(7),此定义的合理性将于后文讨论。

(7)

3.3 PBG-CPW的频率特性分析

PBG-CPW的其等效电路如图2所示,两种传输线除特性阻抗不同外,相应的相位常数也不相同,分别为β1和β2.若标准传输线的传输矩阵为T0,CPW和PS CPW短截线的传输矩阵分别为T1和T2,则所提出传输线的整体传输矩阵可写作T=(T1T2)R,其中指数R为单元结构的重复次数,由此可进一步求得该传输线的散射参量。现取介电常数εr=9.6,介质厚度h=0.8 mm,CPW的参数为wc=0.3 mm,ws=0.2 mm,此时由保角变换求得εeff=5.17,Z0=57.64;取p1=0.1 mm,相应PS CPW的有效介电常数εeff2=2.89,m=0.748 4[6].取传输线长度L=4 mm,n=0.5,针对S=0.2 mm、0.4 mm、1.0 mm和2.0 mm的情况分别使用MATLAB进行传输矩阵和散射矩阵的计算,对应的重复次数R为20、10、4、2.频率扫描范围选为0.01～20 GHz,结果如图3所示。

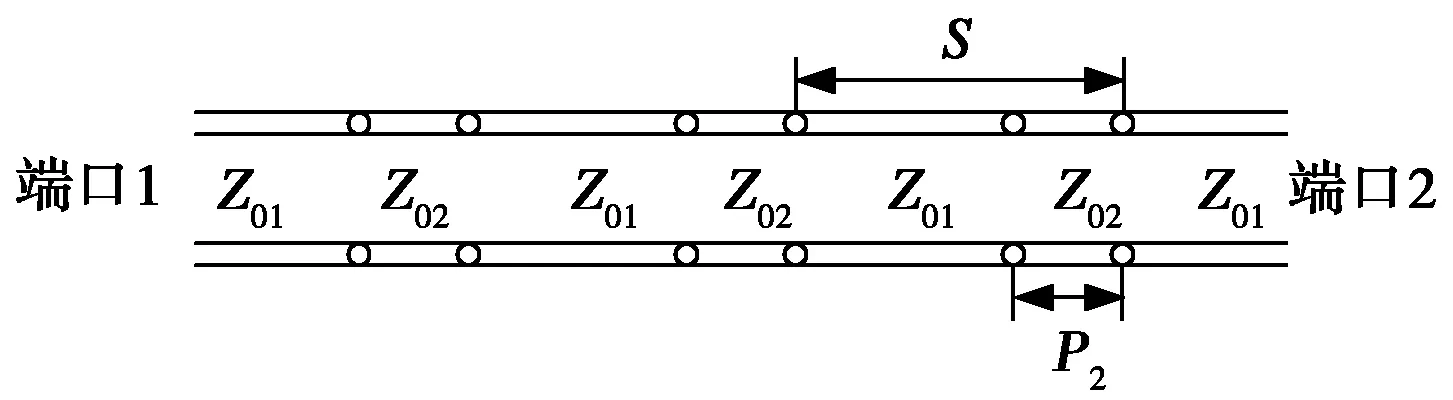
图2 PBG-CPW的等效电路模型

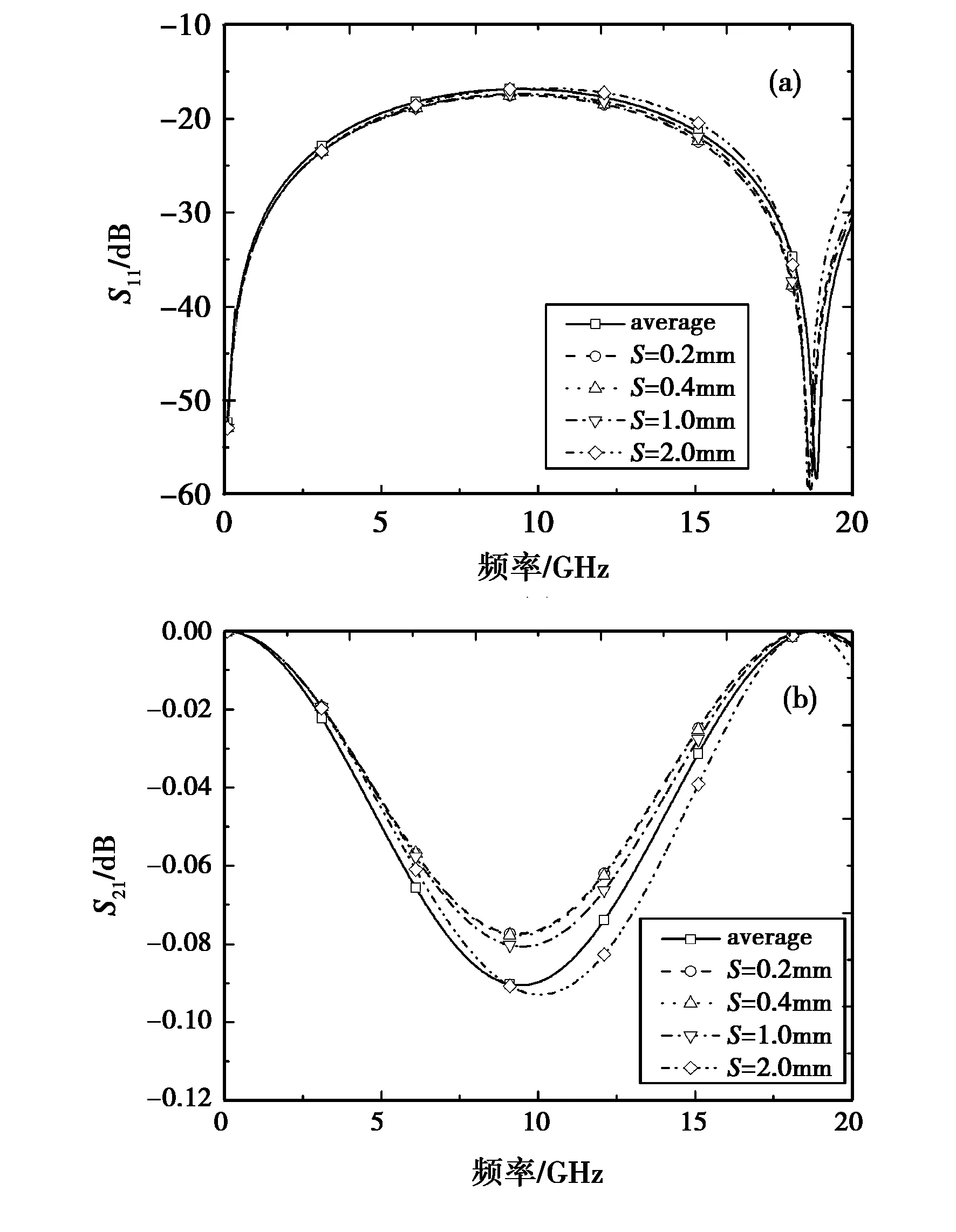
图3 PBG-CPW的频率特性曲线(a)回波损耗;(b)插入损耗

图3中,average对应的曲线为采用式(2)、(3)、(7)式定义的平均参数求得的等效成均匀传输线的计算结果,其中,εeffa=3.95,Z0a=65.96 Ω.可看出对重复周期S=0.2-2 mm的范围,给定m和n,传输特性S21几乎不受S影响,且基本与平均参量结果一致。扩大扫频范围后,S21参数呈周期变化,但频率高于某一值,S21突然恶化,周期单元陷于谐振,呈明显禁带特性,如图4所示。

由图4知,给定m、n,S变大,谐振频率降低,与S成反比。为验证前述假设,采用三维仿真软件HFSS(v12)进行计算,求得群时延特性如图5所示。可看出,在20 GHz范围内,PBG-CPW具有和CPW及PS CPW一样平坦的群时延特性,因而之前定义的有效参数是可信的。

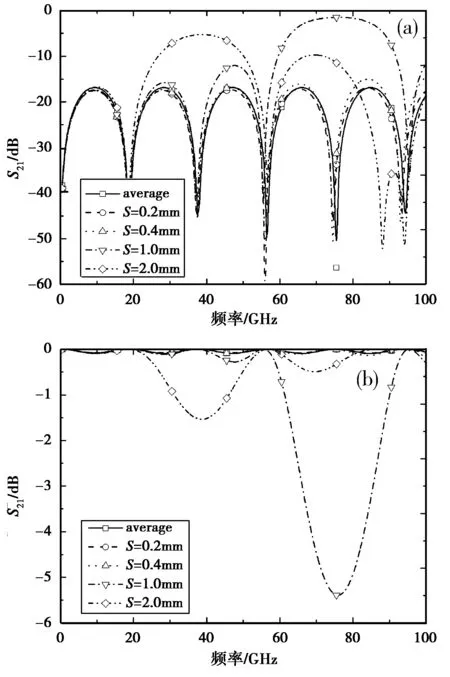
图4 PBG-CPW的宽频S21特性(a)回波损耗;(b)插入损耗

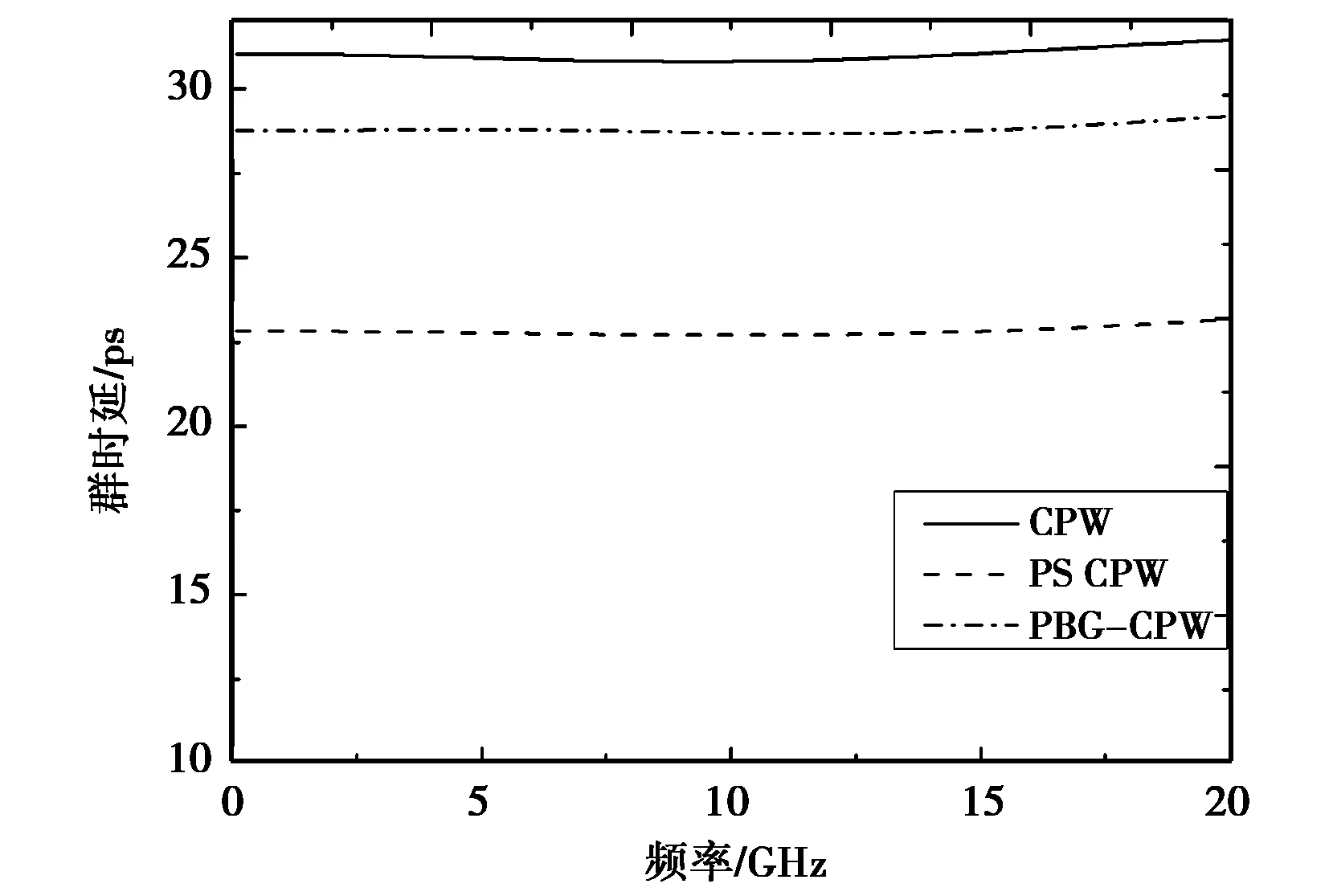
图5 PBG-CPW的群时延特性

4 非对称PBG-CPW结构的分析

弯曲结构是一种常见不连续结构,对电路特性的影响不可忽视,为抑制该结构激发的奇模,可采用空气桥[12]、拐角斜切[13]、速度补偿[14]、相位补偿[15-16]等方式。文献[14]提出了孔缝阵列速度补偿结构,为解决CPW两侧电磁波均衡问题提供了新思路,所提出的部分结构如图6所示,该结构可看作单侧PBG-CPW,即PBG-CPW和CPW的混合结构。该文选用正方形栅格,即p2=p1.在该结构中,两槽的电磁波传输速度不同,因而可在一定程度上补偿弯曲结构中固有的路程差Δl.文献[14]中,孔缝阵列结构的总长度A(原文中以S表示)是由数值方法取得的,求解过程较为费时也较为复杂,采用本文所提出的模型,可有效简化这一过程。

电磁波在上图左右两侧缝隙中的传播速度分别为υpa和υp1,给定结构尺寸时,此值可由前述讨论求得。在文献[14]所讨论的弯角结构中,左侧的传播速度较快,但波程较右侧远。为使两侧信号达到均衡,显然应满足以下条件

(8)

做简单整理可得

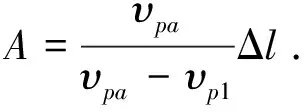
(9)

此即孔缝阵列长度A的表达式,文献[14]针对两组尺寸的孔缝阵列弯角进行了研究,其中前一组为纯仿真验证,而后一组则进行了加工测试。为方便起见,分别称此两种情况为“仿真”和“实物”。本文针对这两组尺寸进行计算。由CPW的计算公式及式(4)知:εeff1S=4.986 8,εeffaS=2.198 8,εeff1M=4.684 6,εeffaM=3.504 6;另于文献[14]中,ΔlS=0.7 mm,ΔlM=4.9 mm.在以上各式的下标中,S代表仿真参数,M对应于实物参数;l代表无PBG栅格一侧,a则代表有PBG栅格一侧。易求得,对仿真数据而言,AS=1.4 mm;对实际测量值,AM=31.4 mm.所求得的结果和文献[14]得到的结果有较好一致性。

5 结束语

所提出的新型PBG-CPW传输线具有较传统CPW更高的设计灵活性及明显的PBG禁带特性。在较低频率之下,其传输特性等同于一段均匀传输线,可通过本文提出的等效相速、等效介电常数及等效阻抗对其进行分析和设计,具有较大的发展空间。所提出的分析方式还可用来分析孔缝阵列速度补偿弯曲结构,较数值仿真计算而言,方便快捷,具有较高的应用价值。

[1]WEN C P.Coplanar waveguide:A surface strip transmission line suitable for nonreciprocal gyro-magnetic device applications [J].IEEE Trans on MTT,1969,17(12):1087-1090.

[2]陈 鹏,房少军.时域有限差分法计算分析非对称共面波导色散特性[J].电子学报,2006(9):1610-1612.

[3]陈 鹏,李晓明,房少军,等.一种超宽带非对称共面波导-槽线转接器的研究[J].电波科学学报，2010,25(3):559-563.

[4]YABLONOVITCH E.Inhabited spontaneous in solid-state physics and electronics[J].Physical Review Letters,1987,58(20):2059-2062.

[5]STRONG J S.Localization of photons in certain disordered dielectric super lattices[J].Physical Review Letters,1987,58(23):2486-2489.

[6]李晓明,房少军,裴 慧,等.一种新型部分介质共面波导[J].大连海事大学学报,2011,37(2):110-112.

[7]PARK J L,KIM C S,KIM J,etal.Modeling of a photonic bandgap and its application for the low-pass filter design[C]//Proc.APMC’99,1999:331-334.

[8]ADISIC V,QIAN Y,COCCIOLI R,etal.Novel 2-D photonic bandgap structure for microstrip lines[J].IEEE Microwave Guided Wave Lett.,1998,8(2):69-71.

[9]KRETLY L C,MARANGONI L C,SILVA A T A.Photonic band gap metallic 2D matrix applied to microstrip CPW lines to operate at Ka band[C]//Microwave and Optoelectronics Conference,2001:435-438.

[10]KRETLV L C,TAVORA A S.A PBG-Photonic Band Gap-static phase-shifter for steerable antenna array[C]//Microwave and Optoelectronics Conference,2003:211-214.

[11]TONG Mingsze,LU Yilong,ZHANG Y P,etal.Spectral analysis of defective photonic band-Gap (PBG)structures on coplanar waveguide (CPW)[C]//34th European Microwave Conference,2004:261-264.

[12]DIB,N I,KATEHI P B,PONCHAK G E.Analysis of shielded CPW discontinuities with air-bridge[C]//IEEE MTT-S Int.Microwave Symp.Dig.,Boston,July 1991:469-472.

[13]WATSON P M,GUPT K C.EM-ANN modelling and optimal chamfering of 90° CPW bends withair-bridges[C]//IEEE MTT-s Int.Microwave symp.Dig.,Denver,CO,June 1997:1603-1606.

[14]张 卉,王均宏.奇模抑制孔缝阵列速度补偿型弯曲共面波导[J].电波科学学报,2009,24(2):228-232.

[15]李晓明,房少军,付世强.一种非对称共面波导相位补偿弯曲结构[J].电波科学学报,2011,26(1):84-89.

[16]LI Xiaoming,FANG Shaojun,PEI Hui,etal.Novel CPW-ACPW phase compensated structure in CPW bend[C//ISAPE 2010,Guangzhou,2010:1-3.