一种新的导航接收机抑制窄带干扰算法
任 超,胡 刚,温景阳,郑永翔,于亚静
(北京北斗星通导航技术股份有限公司,北京 100094)
0 引 言
在通信、雷达等领域的信号处理过程中,通常有用信号在传输和接收过程中会受到外界噪声或本机干扰的污染。通过滤波器抑制噪声或干扰并保留信号能量,是一种干扰对消的过程。这样的滤波器,可以是固定的,也可以是自适应的,而自适应干扰对消器以其自身调节参数的能力以及对信号和干扰的先验知识要求较少的优势得到了广泛应用,有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器[1-2]是时域窄带干扰抑制的主要方法。
FIR滤波器在扩频通信系统窄带干扰抑制中显示出不足。这是因为:为了保留有用信号,总是希望得到一个足够尖锐的带阻滤波器,它的中心频率和要抑制的干扰信号频率一致。为了获得满意的尖锐截止特性,FIR滤波器通常需要的阶数相当高,从而导致计算量很大。对于相同的陷波带宽,实现相似的陷波性能,自适应IIR陷波器和相应的FIR相比,需要相当少的滤波系数。因此,IIR滤波器变得极具吸引力。IIR陷波器是指在单位圆上它的幅频响应在一个特定的值时变为零,我们把这个频率称为陷波频率,并且它的幅度响应在单位圆上的其它点几乎是连续不变的。利用二阶IIR滤波器就可以得到具有尖锐截止特性滤波效果。
1 格型IIR陷波器
Cho等人提出的格型陷波器结构[3-4]框图如图1所示。

图1 格型IIR陷波器结构框图
格型陷波器结构框图上方的格型滤波器H1(z)的输入为x(n),输出为s0(n);而下方的格型滤波器H2(z)的输入为s0(n),输出为s2(n).
由结构框图容易写出格型滤波器H1(z)和H2(z)的输入、输出方程,分别为
s0(n)+a0(1+a1)s0(n-1)+a1s0(n-2)=x(n),
(1a)
s0(n)+k0(1+k1)s0(n-1)+k1s0(n-2)=s2(n),
(1b)
或写成Z变换形式
[1+a0(1+a1)z-1+a1z-2]S0(z)=X(z),
(2a)
[1+k0(1+k1)z-1+k1z-2]S0(z)=S2(x).
(2b)
因此,两个格型滤波器的传递函数分别定义为
(3a)
(3b)
由此得整个格型滤波器的传递函数为
(4)
可见,格型陷波器结构框图上方的格型滤波器H1(z)贡献为整个格型滤波器的极点部分,相当于AR模型;而下方的格型滤波器H2(z)则贡献为整个格型滤波器的零点部分,它是一个格型FIR滤波器。因此,整个格型滤波器具有无限多个冲激响应,为IIR格型滤波器。
由于式(4)必须满足陷波器的条件式
(5)
故有
a0(1+a1)=αk0(1+k1),
(6)
a1=α2k1,
(7)
以上两式给出
(8)
上面的式子说明,权系数a0和a1由权系数k0和k1确定。由于α接近于1,因此,有以下近似关系式:
a1=α2k1≈αk1,
(9)
a0(1+a1)=αk0(1+k1)
≈k0(1+αk1)≈k0(1+a1),
(10)
即a1≈α,α0≈k0.这表明,只需要推导k0和k1的自适应更新公式即可。
这样,整个格型滤波器的传递函数为
(11)
由于H1(z)是一极点模型,为保证这一滤波器的稳定性,H1(z)的极点必须位于单位圆内,即权系数的模|a0|和|a1|都必须小于1.因此,H2(z)的权系数的模型|k0|和|k1|也必须小于1.
权系数k0和k1,可以运用格型FIR滤波器的自适应算法进行自适应调节[5-7]:
(12)
Cm(n)=λCm(n-1)+(1-λ)sm(n)rm(n-1),
(13)
Dm(n)=λDm(n-1)+(1-λ)×
(14)
式中,m=0,1,遗忘因子0<λ<1,而sm(n)和rm(n)分别是格型陷波器结构框图下方的格型滤波器第m级的前向和后向残差。
2 改进格型陷波器设计
可以简化格型陷波器权系数的求解算法,将格型陷波器的零点限制在单位圆上意味着固定k1为1.因此,只需采用自适应算法估计k0的值,即
(15)
C0(n)=λC0(n-1)+(1-λ)s0(n)r0(n-1),
(16)
(17)
为使对k0的估计更加准确,采用如下的处理方法:
(18)
k0(n)=γk0(n-1)+(1-γ)k0(n),
(19)
式中,0<γ<1是平滑因子。
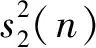
s2(n)=r1(n-1)+s1(n),
(20)
r2(n)=s1(n)+r1(n-1).
(21)
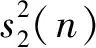
s1(n)=s0(n)+k0(n)r0(n-1),
(22)
r1(n)=k0(n)s0(n)+r0(n-1).
(23)
综合上式解得
s2(n)=k0(n-1)s0(n-1)+k0(n)r0(n-
1)+r0(n-2)+s0(n).
(24)
假定自适应估计值k0(n-1)近似等于k0(n),则代价函数可以表示为
(25)
式中
A(n)=s0(n-1)+r0(n-1),
(26)
B(n)=r0(n-2)+s0(n),
(27)
可得到下列递推式
(28)
C(n)=λC(n-1)+A(n)B(n),
(29)
D(n)=λD(n-1)+A2(n),
(30)
式中,0≤λ≤1.
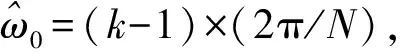
3 性能仿真
通过计算机仿真说明改进格型IIR陷波器的性能。仿真实验如下:输入有用信号s(t)=PNcos(2πfct),它是20 MHz带宽扩频信号,中心频率fc为15.48 MHz,输入窄带干扰信号是频率fj为10 MHz的正弦波,j(t)=Acos(2πfjt),产生的热噪声是接收带宽内高斯白噪声,采样频率fs为62 MHz.输入SIR为-60 dB,输入SNR为-32.0 dB.
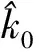
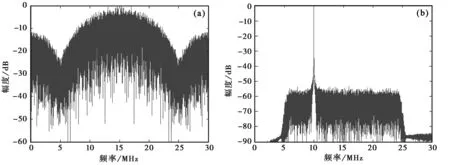
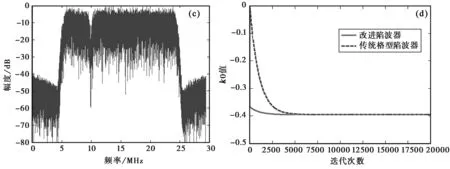
图2 改进格型IIR陷波器窄带干扰抑制结果(a)输入有用信号频谱(b)接收信号频谱;(c)改进格型陷波输出信号频谱;(d)权系数k0收敛曲线
4 结束语
实际通信中电磁环境相当复杂,存在模式繁多和统计特征时变的人为干扰,尤其是高功率密度的窄带干扰已经成为破坏通信系统最主要的因素之一。干扰会导致接收机捕获时间延长、虚警概率增加,严重的会造成接收机失锁而无法工作。针对窄带干扰抑制问题,对二次格型IIR陷波器进行理论推导,并在此基础上提出了改进格型IIR陷波器设计,通过频点估计初始化陷波器参数值,有效提高了二次格型IIR陷波器的收敛速度,最后,计算机仿真两种算法权系数的收敛曲线,验证了改进算法的收敛效果。
[1]西 蒙,赫 金.自适应滤波器原理[M].4版.北京:电子工业出版社,2003.
[2]GRAY A H,MARKEL J D.A normalized digital filter structure[J].IEEE Trans on Acoustics,Speech and Signal Processing,1975,23(3):268-277.
[3]CHO N I,CHOI C H,LEE S U.Adaptive line enhancement by using an IIR lattice notch filter[J].IEEE Trans on Acoustics,Speech and Signal Processing.1989,37(4):585-589.
[4]Makhoul J,COSSELL M.Adaptive lattice analysis of speech[J].IEEE Trans on Acoust,Speech,Signal Processing,1981(29):654-659.
[5]RAO D V R,KUNG S Y.Adaptive notch filtering for the retrieval of sinusoids in noise[J].IEEE Trans on Acoustics,Speech and Signal Processing,1984,32(4):791-802.
[6]CHICHARO J,NG T.Gradient-based adaptive IIR notch filtering for frequency estimation[J].IEEE Trans on Acoust,Signal Processing,1990,38(5):769-777.
[7]TAN Xiaobo,ZHANG Hang.A novel adaptive IIR notch filter for frequency estimation and tracking[C]∥IEEE International Conference on Computer Science and Information Technology,2010:259-263.

