BPSK和BOC(14,2)信号的抗干扰性能分析

郑瑞锋,陈向东

(1.华东师范大学,上海200062; 2.61175部队,江苏 南京210049)

0 引 言

随着卫星导航系统的发展,新的卫星信号体制逐步采用BOC调制方式实现,例如GPS L5频点使用MBOC调制,GALILEO E1频点使用MBOC调制,E5频点使用AltBOC调制。我国北斗卫星导航系统一期区域系统已经建设完成,对北斗系统的推广和应用有着重要的意义。根据未来北斗系统频点规划,北斗B1频点将和GPSL1频点共用;但是目前GPS L1的用户最低接收功率为-158.5 dBW,而北斗系统BOC(14,2)的用户最低接收功率为-161 dBW,两者相差2.5 dB,是否会带来北斗信号和GPS信号之间的相互干扰呢?本文针对BOC(14,2)调制信号受到GPS L1信号的干扰性能进行了分析,能够为北斗全球系统的信号体制设计提供一些参考。

1 BOC信号和BPSK-R(1)信号的仿真分析对比

根据2010年9月中美第五次频率协调会谈上双方达成的会议纪要的要求,北斗系统B1频点信号将采用的中心频点为1 575.42 MHz,具备公开播发和授权使用两种形式。其中公开信号的调制方式为MBOC(6,1,1/11),码速率为1.023 MHz,电文速率为50/100 bps;而授权信号的调制方式为BOC(14,2),码速率为2.046 MHz,电文速率为50/100 bps.本文针对BOC(14,2)信号和BPSK-R(1)信号体制进行分析。

1.1 BOC(14,2)信号仿真

根据BOC信号的模型与特性,BOC信号建模时可以视为BPSK信号与一个副载波相乘。其中BPSK信号的时域表达式为[1]

(1)

根据BOC(14,2)信号的定义,B1频点的副载波频率为14×1.023 MHz=14.322 MHz,B1频点的码速率为2×1.023 MHz=2.046 MHz.因此B1频点的方波半周期数k的表达式为[1]

(2)

式中:Tc为码周期;Ts为副载波的半周期,因此k=14.B1频点的基带信号时域表达式可表示为

gB1=gBPSK(t)sgn(cos(πt/Ts)).

(3)

在分析导航信号的过程中,需要计算导航信号的自相关函数和功率谱密度。其中计算自相关函数为

(4)

利用matlab进行基带信号仿真,计算其自相关函数,可得B1频点的自相关函数如图1所示.

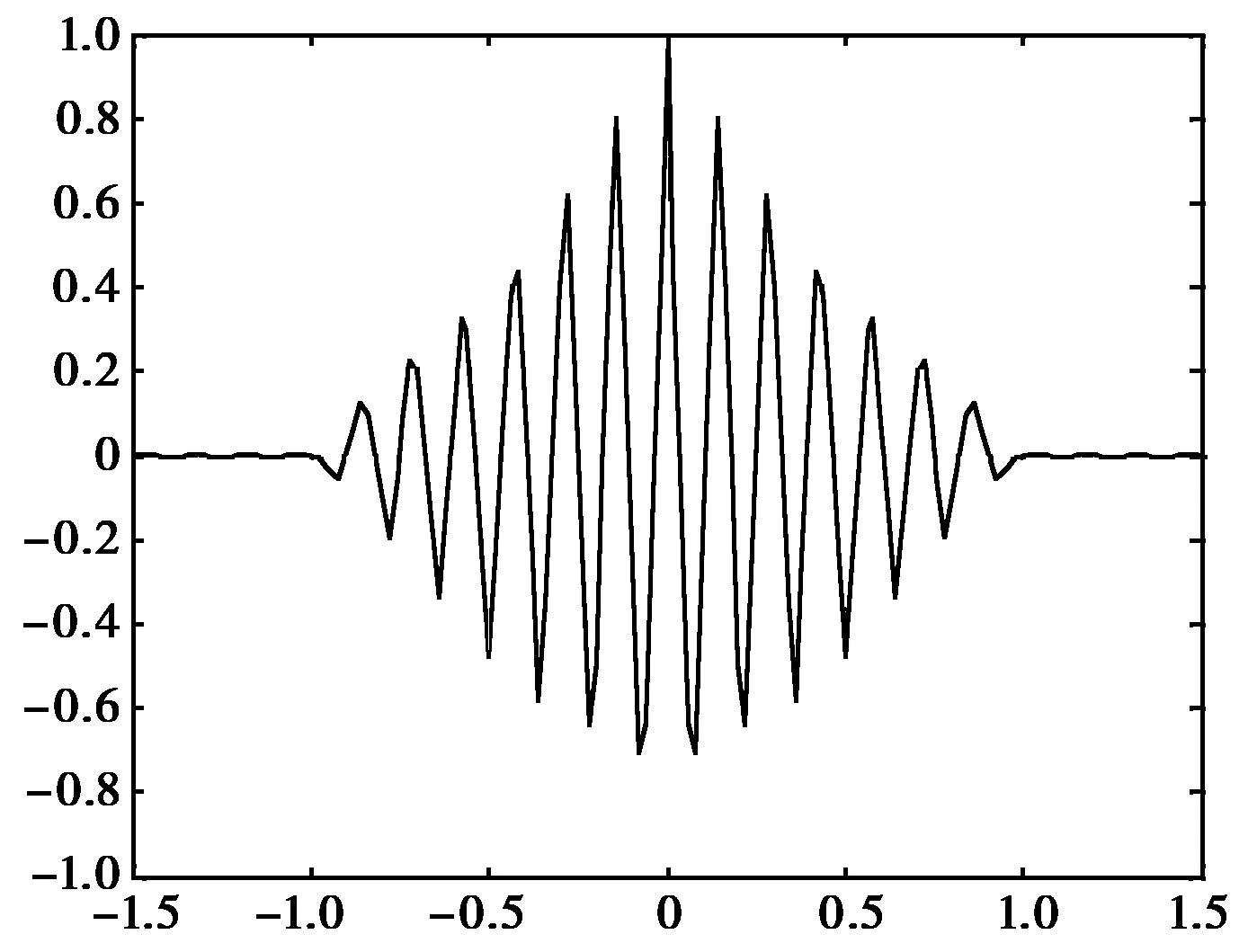
图1 BOC(14,2)自相关函数

由图1可见,BOC(14,2)信号自相关函数正峰和负峰之和具有27个,两峰之间的距离是Ts,主瓣宽度为2/14个码片,因为主峰宽度比较窄,所以可以提高信号的跟踪精度。

B1频点的功率谱密度[3]为

(5)

根据式(5),可以对B1频点的信号进行仿真,得出BOC(14,2)的基带频谱曲线如图2所示.

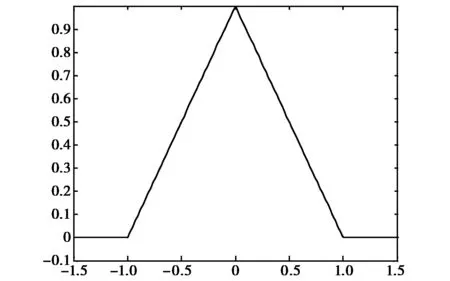
图2 BOC(14,2)归一化信号功率谱曲线

1.2 BPSK-R(1)信号仿真

对GPS L1频点的BPSK-R(1)信号进行基带仿真,可得L1频点的自相关函数如图3所示。

图3 BPSK-R(1)自相关函数

L1频点的功率谱密度为

SBPSK-R(f)=Tcsinc2(πfTc).

(6)

根据式(6),可以对L1频点的信号进行仿真,得出BPSK-R(1)的基带频谱曲线如图4所示。

图4 BPSK-R(1)归一化功率谱曲线

1.3 两种信号参数对比

根据以上对两种信号的自相关函数和功率谱函数对比,可以得出BOC(14,2)信号具有以下优点:

1)BOC(14,2)信号的自相关函数比BPSK-R(1)更加尖锐,可以提高抗干扰性能;

2)BOC(14,2)信号的功率谱包含两个边带,可以分别利用两个边带的信号进行捕获跟踪;

3)BOC(14,2)信号的频谱主峰宽度比BPSK-R(1)信号窄。

2 干扰参数计算和分析

为分析GPS L1频点BPSK-R(1)信号和北斗B1频点BOC(14,2)信号的相互干扰,需要从抗干扰品质因数Q值、干扰容限J值、载波跟踪门限J/S值和干扰距离[1-5]进行对比分析。

2.1 抗干扰品质因数Q值分析

抗干扰品质因数Q值反映了导航信号的抗干扰效果,Q值越大,抗干扰效果越好。对应于不同的干扰信号类型,Q值的取值不同[1]。根据文献[1],抗干扰品质因数Q值简化计算公式为

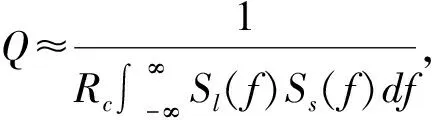
(7)

式中:Rc为码速率;Sl为干扰信号的功率谱密度;Ss(f)为导航信号的功率谱密度。

本文的分析内容主要考虑L1信号和B1信号之间的相互干扰,因此在计算B1频点的抗干扰品质因数Q时将L1频点信号作为干扰信号,B1频点信号作为接收机收到的有用信号;在计算L1频点的抗干扰品质因数Q时将B1频点信号作为干扰信号,L1频点信号作为接收机收到的有用信号。

因为B1频点和L1频点的中心频率相同,所以计算Q值时可以分别对两个信号之间的有效带宽进行计算。计算B1频点的Q值时可以设置为双边带的带宽(40 MHz)和单边带带宽(20 MHz),计算L1频点的Q值时设置带宽为5 MHz.用matlab软件仿真出的归一化功率谱密度,再通过积分函数trapz进行仿真计算,可以得出两种信号相互干扰时的抗干扰品质因数Q值表,可见B1信号在两种边带计算条件下的Q值都远大于L1信号。

表1 抗干扰品质因数Q值计算表

2.2 J/S值对比分析

干扰信号的影响是降低接收机的载噪比(C/N0),进而影响到接收机的信号捕获、跟踪和数据解调。J/S值是天线输入端干扰和有用信号功率之比,反映了系统的抗干扰能力[4]。J/S值的计算如式(8)所示。

(8)

式中:Gsv代表卫星的天线增益;Gj为干扰方向的天线增益;Q为抗干扰品质因数;Rc为码速率,Cs/N0为接收机输入信号载噪比; (Cs/N0)eff为跟踪门限,代表接收机正常工作时的最小等效载噪比。

对应北斗 B1频点信号,一般情况下可设接收机系统的参数[2]为

Gsv=1.5 dB;Gj=-3 dB;Rc=2.046 MHz;Q=4.56; (Cs/N0)=42 dB-Hz; (Cs/N0)eff=28 dB-Hz;可得:J/S=46.0 dB.

对应GPS L1频点信号,一般情况下可设接收机系统的参数为

Gsv=1.5 dB;Gj=-3 dB;Rc=1.023 MHz;Q=1.5; (Cs/N0)=42 dB-Hz; (Cs/N0)eff=28 dB-Hz;可得:J/S=38.2 dB.

为研究两种信号在跟踪门限(Cs/N0)eff变化及输入信号载噪比(Cs/N0)变化条件下J/S的变化,仿真J/S变化曲线如图5和图6所示。

图5 J/S值随跟踪门限变化曲线

图6 J/S值随输入信号载噪比变化曲线

2.3 干扰容限J值计算分析

因为存在多个信号功率电平,干扰容限J(可容忍的干扰)是考察抗干扰性能更加直观的指标。干扰容限等于J/S值加上最小接收功率电平Sr.

北斗B1频点的最小接收功率电平Sr(B1)是-161 dBW,GPS的L1频点的最小接收功率电平Sr(L1)是-158.5 dBW.通过下表可以看出常规条件下两种信号的干扰容限J值。

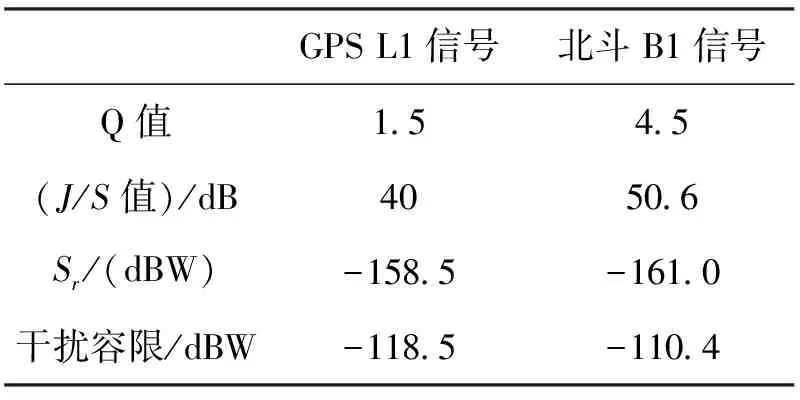
表2 干扰容限J值比较表

为了进一步分析在跟踪门限和输入载噪比变化条件下干扰门限值的变化规律,仿真如下曲线:图7是干扰容限随跟踪门限变化的曲线图,图8是干扰容限随输入载噪比变化的曲线图。

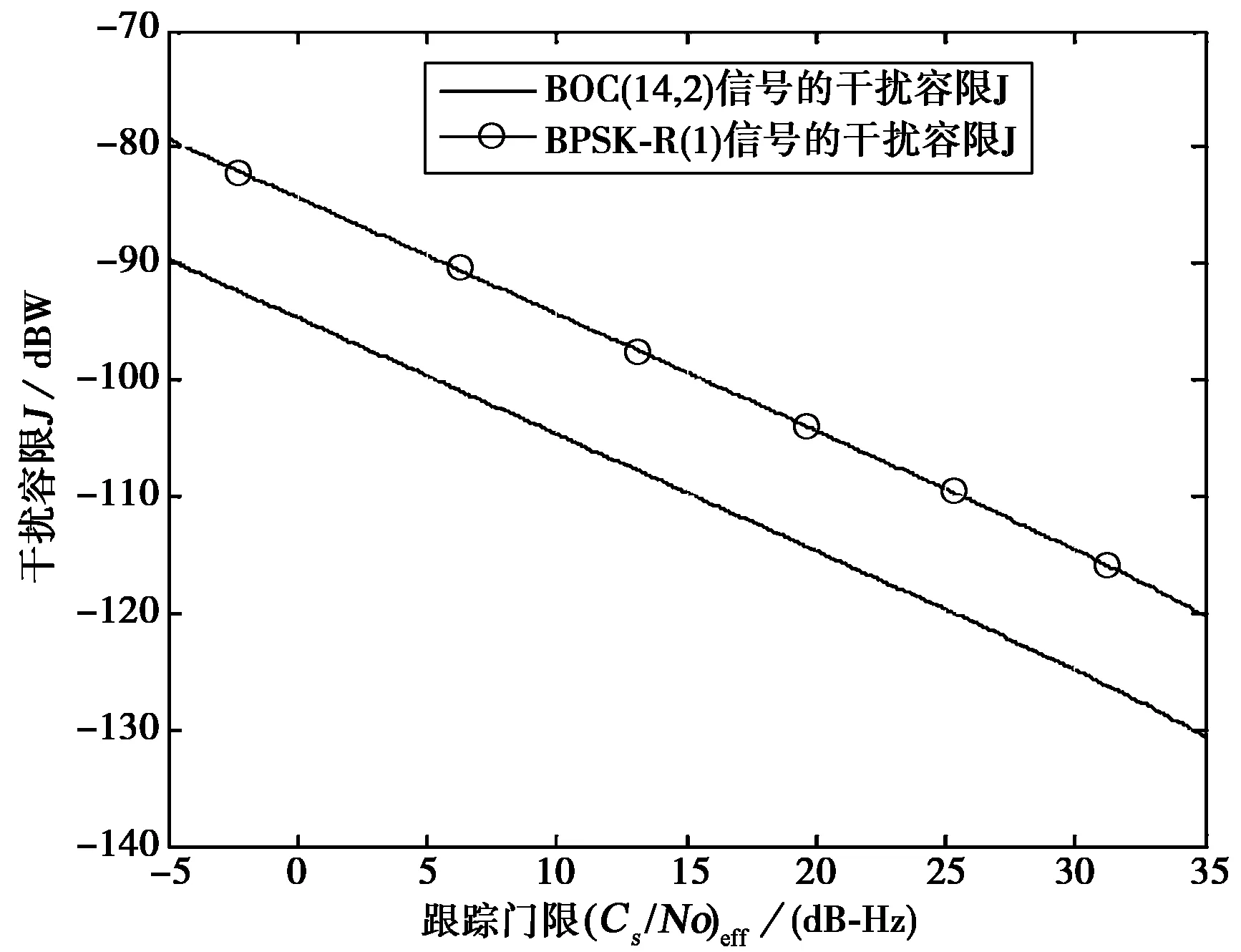
图7 干扰容限随跟踪门限变化曲线

图8 干扰容限随输入信号载噪比变化曲线

2.4 RF干扰距离计算及对比分析

在考察接收机与干扰源之间的距离[4]关系时,经常考察的指标是干扰源的等效各向同性辐射功率(EIRP)。

因为EIRP、干扰容限和干扰距离之间的关系可以由式(9)至式(12)[1]计算:

(EIRP)dB=(J)dB-(Gj)dB+

(Lp)dB+(Lf)dB,

(9)

(EIRP)dB=10×log((EIRP)W),

(10)

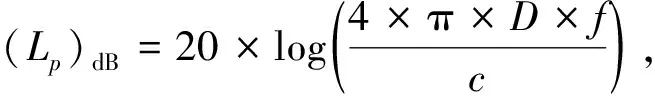
(11)

(12)

其中:(J)dB为干扰容限; (Gj)dB为接收机天线增益; (Lp)dB 为自由空间传播损耗; (Lf)dB为接收机前端滤波器引起的干扰功率损耗,考虑到通用接收机前端没有进行特殊抗干扰处理,设(Lf)dB=0.根据2.3节表2的计算结果,设置北斗B1频点的J=-110.4 dBW,设置GPS L1频点的J=-118.5 dBW,根据式(12)可以得出两种信号的干扰源功率和干扰距离之间的相互关系曲线如图6所示。由曲线的对比可以看出,相同的干扰功率下,北斗B1频点接收机可以容忍的干扰距离更短,说明北斗B1频点的抗干扰性能优于GPS L1频点。

3 结束语

本文通过抗干扰品质因数Q值、J/S值、J值和干扰距离的分析可见,BOC(14,2)信号相比于BPSK-R(1)信号的抗干扰能力更强,具有更优的干扰距离。通过本文的相关分析数据可以给未来北斗系统的应用提供一些有益的参考。

[1]艾利奥·D·卡普兰，克利斯朵夫·郝加蒂.GPS原理与应用[M].寇艳红 译.电子工业出版社,2007.

[2]王 璐,刘崇华,何善宝.导航BOC信号的抗干扰性能分析[J].中国空间科学技术学报,2009(4):69-76.

[3]杨 力,薄煜明,田明浩.BOC调制信号的抗干扰性能研究[J].计算机科学,2008,35(4);33-35,59.

[4]刘凯燕,李存志,王 超.GPS接收机宽带噪声干扰性能分析与仿真[J].河南科学,2006,24 (1):69-73.

[5]刘禹圻,胡修林,冉一航,等.卫星导航信号抗单频干扰性能研究[J].电子学报,2011,20(6):1410-1416.