卫星导航信号波形畸变引起的码跟踪偏差

徐 赟，刘建成，桑怀胜

(北京卫星导航中心，北京 100094)

0 引 言

自从GPS SV19号卫星被发现信号异常以来，卫星导航信号质量问题受到越来越多地重视，而卫星导航信号异常对导航接收机的影响是一项重要的研究内容[1-4]。针对卫星载荷可能出现的故障现象，许多文献提出了各种不同的故障模型，而 2OS模型是国际民航组织认可的卫星导航信号畸变模型[5]。该模型把数字电路故障、模拟电路故障和混合电路故障引起的畸变波形分别称为TMA、TMB和TMC，由超前/滞后参数、震荡频率和衰减因子等3个可变参数来定义[6]。2OS模型被广泛应用于导航信号质量监测及标志为可用卫星的模型参数估计[5-7]。

由于卫星导航信号异常导致接收机相关函数异常，从而改变DLL的鉴别函数特性，最终导致码跟踪产生偏差。监测接收机的伪距测量在卫星导航系统中用于导航卫星的定轨和星地时间同步，伪距测量决定卫星导航系统的服务精度，因此为确定信号异常对导航卫星定轨和星地时间同步的影响需要定量分析卫星导航信号异常引起的伪码测距的变化。

文献[8]分析了载波泄露和频谱非对称性异常对码跟踪误差的影响。文献[9]通过对卫星载荷模拟单元部分的建模，研究了宽带卫星导航信号经模拟单元处理后的码跟踪偏差。文献[10]研究了正弦幅度波动、正弦相位波动、带限和杂散发射等线性信号畸变及非恒包络调制(THP)对伽利略码跟踪精度的影响。文献[11]和[12]研究了基于2OS模型在BOC调制情况下的码跟踪偏差，数值分析了多个固定2OS模型参数码跟踪偏差随相关器间隔变化情况。但上述文献没有分析故障模型参数空间范围内引起的码跟踪偏差。由于现实情况下监测接收机的相关器间隔不能随意改变，因此需要研究相关器间隔固定时故障模型参数空间范围内的波形畸变引起的码跟踪偏差。通过数值分析更直观显示故障模型参数空间范围内的所有可能波形畸变引起的码跟踪偏差，并进一步给出最大超前偏差和最大滞后偏差。

1 卫星导航畸变波形

TMA畸变波形用伪随机码码片的下降沿超前或滞后来实现数字电路故障的建模[5]。该模型只有一个可变参数Δ，即超前/滞后参数，表示伪随机码码元的下降沿超前或滞后多少。参数空间范围是-0.12≤Δ≤0.12.

TMB畸变波形用衰减二阶响应作为对模拟电路故障的建模，即[5]

式中:fd为震荡频率；σ为衰减因子；参数空间范围是7.3≤fd≤13 MHz，0.8≤σ≤8.8 Mn/s.

TMC畸变波形是TMA模型和TMB模型的综合，以实现对混合故障的建模。该模型包括三个可变参数Δ 、fd和σ，参数空间范围同TMA模型和TMB模型。

2 2OS畸变波形的DLL鉴别器特性

典型的GNSS接收机对距离的测量是通过DLL对接收信号的伪码跟踪来实现的。忽略导航数据信息的GNSS接收机信号模型为

sR(t)=A·p(t-τ0)sin(2πf0t+φ0)+n(t).

(2)

式中:A为接收信号幅度;p(t-τ0)为导航卫星下播的伪码波形;τ0为传播时延;φ0为相位;f0为频率;n(t)为接收机噪声。

射频估计误差忽略不计，经混频和滤波后，接收信号可表示为

sR(t)=A·p(t-τ0)sinφ0+n(t).

(3)

当相关器间隔为Td时，在DLL环路中本地产生即时、超前Td和Td滞后三个相位的扩频码。三路本地信号与接收信号相关处理后，即时、超前和滞后三个通道的I、Q支路输出分别为

(4a)

(4b)

(4c)

(4d)

(4e)

(4f)

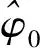
考虑导航接收机常用的三种类型的DLL鉴别器，分别为相干鉴别器、功率模式的非相干鉴别器和点积模式的非相干鉴别器。假设相位估计误差可忽略，则相干鉴别器输出为

(5)

功率模式和点积模式的非相干鉴别器输出分别为

Dm=IE2+QE2-IL2-QL2

(6a)

Dm=(IE-IL)IP+(QE-QL)QP

(6b)

导航接收机的DLL尽可能地跟踪鉴别器曲线的零交叉点，使输入的码跟踪误差最小。如果导航接收机接收到正常导航信号，在稳态跟踪时鉴别器输出为零时，码跟踪误差也为零。但是，卫星导航波形畸变使零交叉点偏离了码跟踪误差为零的位置，那么这个偏离量就是导航波形畸变引起的码跟踪偏差的大小，即

(7)

对正常信号和TMA、TMB、TMC三种畸变波形的三种鉴别器特性分别进行数值分析。伪码速率为1.023 Mcps，相关器间隔为0.5个码片。TMA模型参数：Δ=0.1.TMB模型参数：fd=4.5 MHz，σ=1 Mn/s.TMC模型参数：Δ=0.1，fd=4.5 MHz，σ=1 Mn/s.图1示出了上述参数情况下的DLL鉴别器特性。

从图中可以看出，卫星导航畸变波形改变了鉴别器特性，包括：1)改变了鉴别器零交叉点附近的斜率；2)鉴别器输出为零时码跟踪误差不为零，而是有偏离；3)三种鉴别器的偏离量相差很小。

3 码跟踪偏差数值分析

对TMA、TMB、TMC三种畸变波形的码跟踪偏差分别进行数值分析，以研究偏离距离在TMA、TMB、TMC模型参数空间范围内变化情况。由于三种鉴别器的偏离相差不大，因此下面只分析相干鉴别器情况。

3.1 TMA畸变波形引起的码跟踪偏差

数值分析先固定伪码速率为1.023 Mcps，相关器间隔为0.5个码片。图2示出了TMA在威胁参数空间范围内的码跟踪偏差。从图2可以看出，TMA畸变波形引起的码跟踪偏差与超前/滞后参数呈线性关系，而且在威胁参数空间范围内最大码跟踪偏差接近60 ns.当相关器间隔大于0.06个码片时，数值分析结果与相关器间隔为0.5个码片时的结果相同。

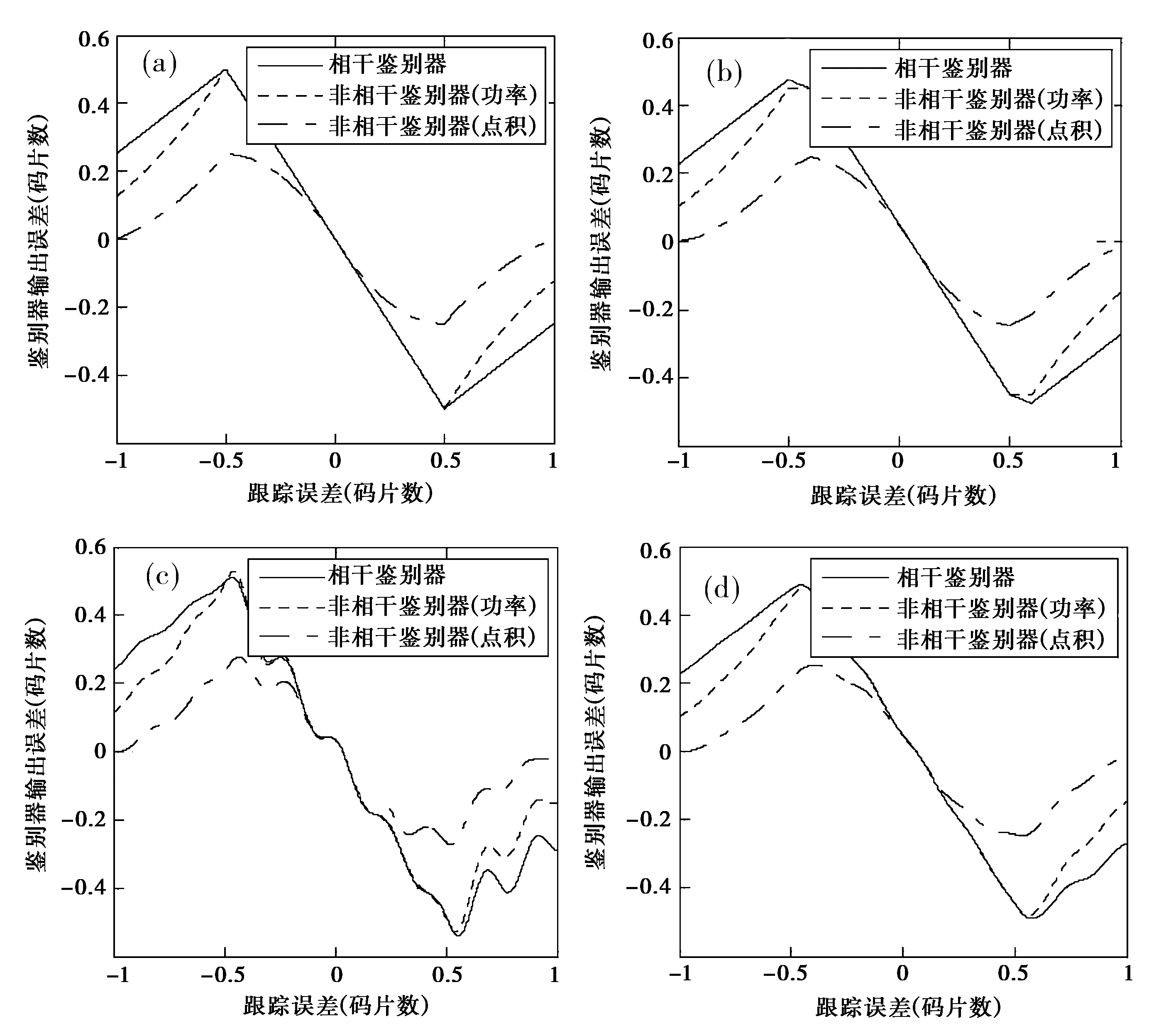
图1 DLL鉴别器特性(a)正常信号;(b)TMA畸变波形;(c)TMB畸变波形;(d)TMC畸变波形

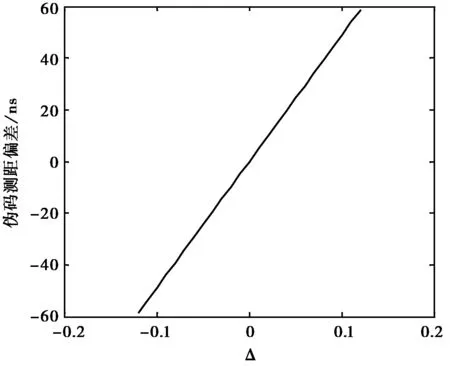
图2 TMA畸变波形引起的码跟踪偏差

3.2 TMB畸变波形引起的码跟踪偏差

数值分析采用震荡频率采样间隔Δfd=0.2 MHz，衰减因子采样间隔Δσ=0.1 Mn/s.固定伪码速率为1.023 Mcps，相关器间隔为0.5个码片，图3示出了TMB在威胁参数空间范围内的码跟踪偏差。从震荡频率参数fd的角度看，码跟踪偏差周期性地出现多个顶峰和谷底。从衰减因子σ的角度看，码跟踪偏差与σ呈反比。

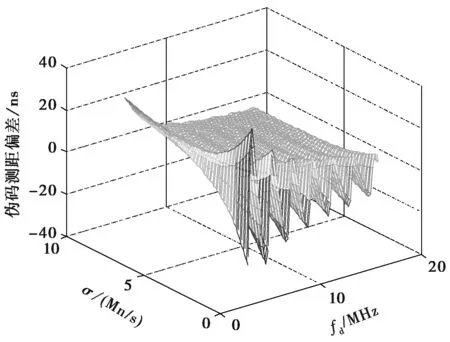
图3 TMB畸变波形引起的码跟踪偏差

在典型的伪码速率和相关器间隔情况下，TMB威胁参数空间范围内码跟踪的最大超前偏差和最大滞后偏差如表1所示。可以看出，TMB在威胁参数空间范围内码跟踪最大超前偏差和最大滞后偏差与伪码速率和相关器间隔有关，典型参数情况下的最大超前偏差达到26.9 ns，最大滞后偏差达到43.0 ns，最大滞后误差出现在相干间隔较小的情况。

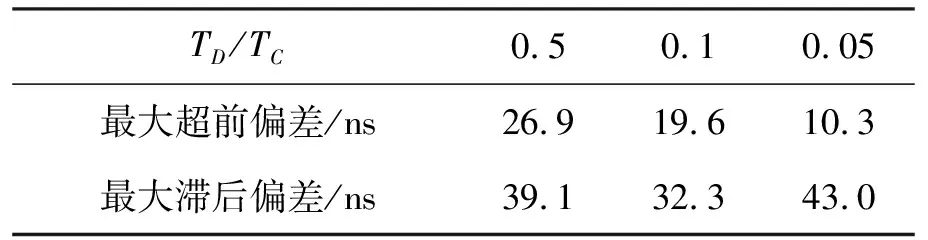
表1 TMB在威胁参数空间范围内码跟踪最大超前偏差和最大滞后偏差(保留小数点后一位)

3.3 TMC畸变波形引起的码跟踪偏差

由于TMC模型是三个可变参数的函数，因此无法给出TMC在威胁参数空间范围内的码跟踪偏差示意图。数值分析采用超前/滞后参数Δ的采样间隔为0.01，震荡频率采样间隔Δfd=0.2 MHz，衰减因子采样间隔Δσ=0.1 Mn/s.表2示出了在典型的伪码速率和相关器间隔情况下，TMC威胁参数空间范围内码跟踪的最大超前偏差和最大滞后偏差。可以看出，TMC在威胁参数空间范围内码跟踪最大超前偏差和最大滞后偏差与伪码速率和相关器间隔有关，最大超前偏差达到88.5 ns，最大滞后偏差达到90.4 ns.

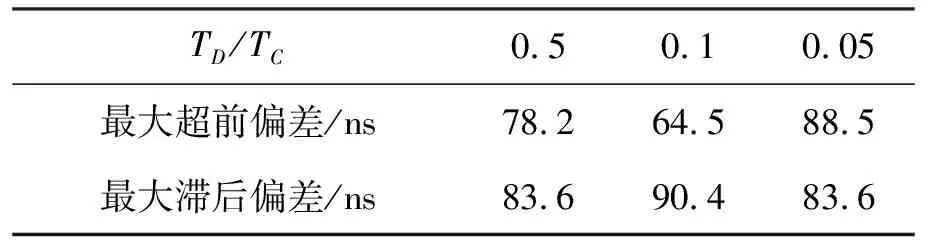
表2 TMC在威胁参数空间范围内码跟踪最大超前偏差和最大滞后偏差(保留小数点后一位)

4 结束语

基于由3个可变参数定义的2OS模型的卫星导航畸变波形，研究了相关器间隔固定时2OS模型参数空间范围内的波形畸变引起的码跟踪偏差。在BPSK调制的GNSS接收机信号模型下，卫星导航波形畸变使相干鉴别器、功率模式和点积模式的非相干鉴别器等三种DLL鉴别器的零交叉点均偏离了码跟踪误差为零的位置，引起码跟踪偏差。对码跟踪偏差的数值分析结果表明：当相关器间隔大于0.06个码片时，TMA畸变波形引起的码跟踪偏差与超前/滞后参数呈线性关系，而且在参数空间范围内最大码跟踪偏差接近60 ns.相关器间隔为0.5、0.1、0.05个码片时，TMB在参数空间范围内码跟踪最大超前偏差达到26.9 ns，最大滞后偏差达到43.0 ns.在同样的条件下，TMC在威胁参数空间范围内码跟踪最大超前偏差达到88.5 ns，最大滞后偏差达到90.4 ns.

[1]卢晓春,周鸿伟.GNSS空间信号质量分析方法研究[J].中国科学：物理学 力学 天文学,2010,40(5):528-533.

[2]王 斌,庞 岩,刘会杰.导航信号有害波形检测技术研究[J].电子与信息学报,2011,33(7):1713-1717.

[3]MACABIAU C,CHATRE E.Impact of evil waveform on GBAS performance[C]//Proceedings of the IEEE PLANS 2000,2000:22-29.

[4]WONG G,PHELTS R E,WALTER T,ENGE P.Bounding errors caused by nominal GNSS signal deformations[C]//Proceedings of the ION GNSS,Manassas,VA:ION GNSS,2011:2657-2664.

[5]MITELMAN A M.Signal quality monitoring for GPS augmentation systems[D].California:Standford University,2004.

[6]PHELTS R E.Multicorrelator techniques for robust mitigation of threats to GPS signal quality[D].California:Standford University,2001.

[7]PHELTS R E,WALTER T,ENGE P.Characterizing nominal analog signal deformation on GNSS signals[C]// Proceedings of the ION GNSS,2009:1343-1350.

[8]HE Chengyan,GUO Ji,LU Xiaochun,WANG Xue,etal.The impact of carrier leakage and spectral asymmetry distortions on the performance of navigation signals[C]//The 3rd China Satellite Navigation Conference,Guangzhou,China:CSNC ,2012:147-160.

[9]CHEN Yibo,KOU Yanhong ,ZHANG Zhengwen.Analog distortion of wideband signal in satellite navigation payload[C]//The 3rd China Satellite Navigation Conference,2012:89-100.

[10]SOELLNER M,KOHL R W,ASTRIUM L,etal.The impact of linear and non-linear signal distortions on Galileo code tracking accuracy[C]//Proceedings of the ION GNSS,2002:1270-1285.

[11]PHELTS R E,AKOS D M.Effects of signal deformations on modernized GNSS signals[J].Journal of Global Positioning Syetems,2006,5(1-2):2-10.

[12]ZHANG Zhengwen,KOU Yanhong,LIU Jiansheng,etal.Analysis of signal distortion impact on code tracking bias for high-order BOC modulation[C]// The 3rd China Satellite Navigation Conference,2012:79-88.