基于遗传算法的桥式网络可靠度和冗余度分配优化
张民悦,李丹丹
(兰州理工大学理学院,甘肃 兰州730050)
0 引言
在实际问题中,有一类既不属于串联又不属于并联的复杂网络系统,即桥式网络系统,如电路桥式网络、通讯桥式网络、交通桥式网络等.在可靠度确定的情况下,提高子系统的冗余数将导致整个系统造价上升,并且由于成本造价、体积、重量等条件的限制,单独依靠提高某个模块的可靠度来提高系统可靠度是困难的,所以通过提高模块的可靠度和增设冗余模块可以保证子系统具有优化配置的可靠度指标.而最优冗余个数和子系统的可靠度有关,因此,模块的可靠度和子系统冗余数应同时优化,以便在限制条件下使整个系统的可靠度最优[1-5].文献[6]中利用MATLAB的BNB20()函数,对串联系统的冗余度和可靠度分配进行整数优化;文献[7]建立了系统可靠性分配优化模型,结合可靠性单元的复杂度、技术成熟度、使用环境等实现广义成本的定量评估,用改进基本遗传算法进行问题的求解;文献[8]中提出了一种改进的遗传算法,并用其求解多目标优化方法;文献[9]建立了系统可靠性分配冗余最优化非线性规划模型,研究了两种不同的解析方法,利用LINGO软件编程进行了验证;文献[10-11]分别研究了定向遗传算法的全局优化和基于矩阵系统的可靠性方法,并将这种方法应用到桥式网络系统中;文献[12]中阐述了遗传算法的一般原理和求解问题的一般过程,讨论了近年来遗传算法在遗传算子、控制参数等方面的改进.
在前面文献的基础上,提出建立子系统可靠度指标和冗余个数一体化并发设计问题,建立带有可选设计的桥式网络系统可靠度和冗余度分配优化模型,最后给出算例,通过遗传算法求解这类非线性连续变量和离散变量混合问题.
1 复杂系统—桥式网络系统模型
在图1所示的桥式网络系统模型中有5个子系统,我们设计带有可选设计和冗余度系统的可靠度,对于每个子系统,设计有多个可选设计αi(i=1,2,3,4,5)来满足可靠性要求,其中αi为第i个子系统可选用的设计,每个子系统我们假定设置mi(i=1,2,3,4,5)个冗余元件并联组成,在造价(Ci),重量(Wi)以及体积(Vi)等条件的限制下,如何对子系统进行可靠度分配以及如何对每个子系统进行冗余数分配是本文中拟解决的主要问题.

图1 桥式网络系统框图
1.1 系统的可靠度 引入概率理论:
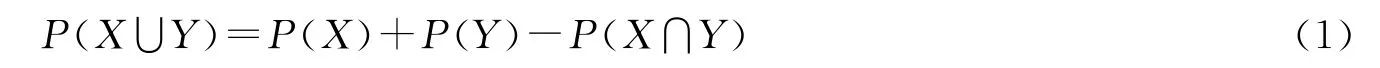
要使系统正常工作,需找出所有从输入端到输出端的可能路径.考虑子系统的组合{1,2},{3,4},{1,5,4}和{3,5,2},只要其中任何一个组合正常工作,则系统就正常工作,这时系统的可靠性为P({1,2}∪{3,4}∪{1,5,4}∪{3,5,2}).设Ri(i=1,2,3,4,5)为第i子系统的可靠度,由概率理论整个系统的可靠度为:
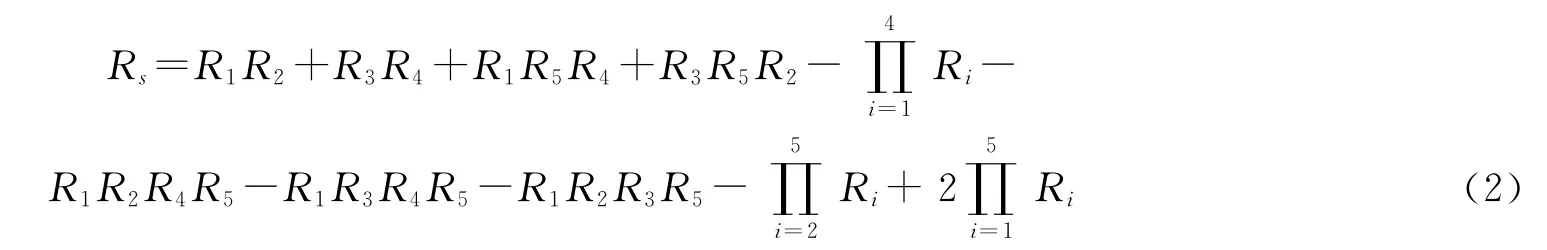
1.2 建立模型 系统由5个子系统构成,对于每个子系统,有多个可选设计来满足可靠性要求,则该模型可以描述为非线性整数规划:

其中
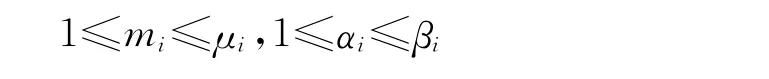
式中,θ为待优化的参数向量;αi(i=1,2,3,4,5)为第i个子系统可选用的设计;mi(i=1,2,3,4,5)为第i个子系统的冗余元件数;μi为第i个子系统的冗余元件上界;βi为第i个子系统可选用设计的上界;R(m,α)为具有冗余元件m和可选设计α的系统可靠度;C(m,α)为系统满足冗余元件m和可选设计α的造价函数;W(m,α)为系统满足冗余元件m和可选设计α的重量函数;V(m,α)为系统满足冗余元件m和可选设计α的体积函数;C*为系统造价的总约束;W*为系统重量的总约束;V*为系统体积的总约束.
每个分系统由冗余元件并联组成,则每个子系统i的可靠度函数为:
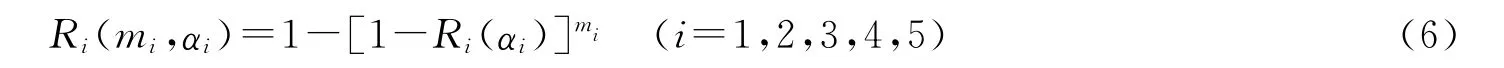
2 优化工具——遗传算法
遗传算法[12-13]是模拟自然界生物进化机制的一种算法,即遵循适者生存、优胜劣汰的法则,也就是寻优过程中将有用的保留,无用的则去除.GA能在许多局部较优中找到全局最优点,是一种全局最优化方法.在科学和生产实践中表现为,在所有可能的解决方法中找出最符合该问题所要求的条件的解决方法,即找到一个最优解.
2.1 遗传算法的可行性分析及运算过程 在可靠性优化方面前人已经做了很多研究,尤其是在冗余元件的最优分配方面.现阶段根据研究可应用于可靠性研究的带有约束条件的数学规划技术的方法主要有动态规划法、直接寻查法等,但是对于大规模的、有多目标函数、非线性的的全局性混合优化问题,被证明有效的算法很少,而且优越性不强.遗传算法作为求解最优化问题的一种智能算法,对目标函数要求低,容易实现、稳定性比较好.而且还具有高度的并行性、随机性以及自适应搜索等技术特点,是一类可用于复杂系统优化问题的鲁棒搜索算法,尤其对于大规模多峰多态函数全局优化问题,在求解速度和质量上远远超过一般方法.
对于上述模型,遗传算法的基本运算过程[14]如下:
1)编码方式.将问题的解用一种码表示,建立数据结构,将遗传算法中的个体与问题的状态空间相对应表示出来,给出优化参数向量θ=[m1,α1,m2,α2…mN,αN]T的解域范围,可选设计α=[α1,α2,α3],冗余数m=[m1,m2,m3,m4,m5]所有分量为整数型.
2)设定种群规模数s=50,交叉概率Pc=0.9,变异概率Pm=0.01,最高进化代数G=200.
3)初始化:采用整数值编码,根据解的可行域随机确定50个个体构成初始群.
4)个体评价:计算群体中各个个体的适应度.适应度函数采用如下线性函数:

其中,Ni为种群大小;P是个体在种群中的位置,该例是最大化目标函数,所以,目标函数值最小的个体P=1,最大的个体P=Ni;sp是选择压力(1≤sp≤2),取sp=1.75.
5)选择运算:把种群中的个体适应度由大到小排序,根据各个个体的适应度确定其繁殖后在交配池中所占比例

6)交叉运算:遗传算法中起核心作用的就是交叉算子.这里采用离散交叉操作方式产生后代,操作为:
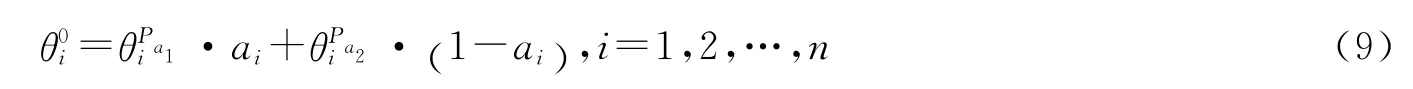
7)变异运算:对种群中的各个个体以变异概率Pm随机改变某一分量的值.
8)终止条件判断:看是否达到最大进化代数,若未达到返回步骤4);若达到,则以进化过程中所得到的具有最大适应度个体所对应的目标函数值作为最优解输出,即全局最优解,终止计算.
2.2 遗传算法的流程图 基本的GA流程图如图2:
3 算例分析及其仿真
这里以一交通网络系统:公路浮箱带式桥结构系统为例,目前我国国内现有浮箱[15]种类很多,如中-60浮箱,东方红浮箱,装配式公路浮箱,TF-82浮箱,松花江浮箱等等,各种浮箱重量,体积,价格不等.系统受造价(Ci),重量(Wi)以及体积(Vi)的限制,C*=5.8万元,W*=40t,V*=225m3.系统的优化设计问题可以描述为:寻求最优的可选设计子系统α1,α2,…,α5,和子系统冗余数m1,m2,…,m5,以使系统在满足总费用,总重量及总体积限制条件下可靠度R最高.
该系统是具有冗余单元和可选设计的桥式网络系统,适用于以下模型:
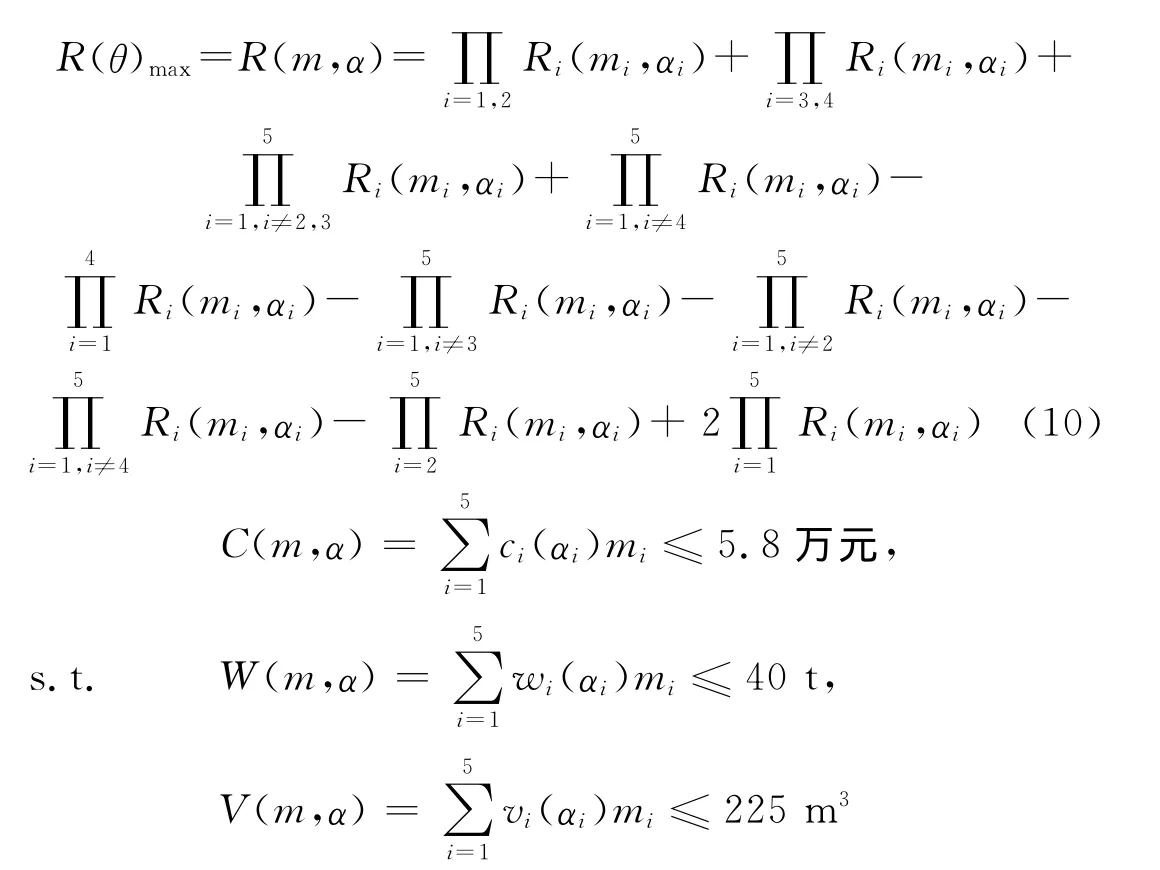

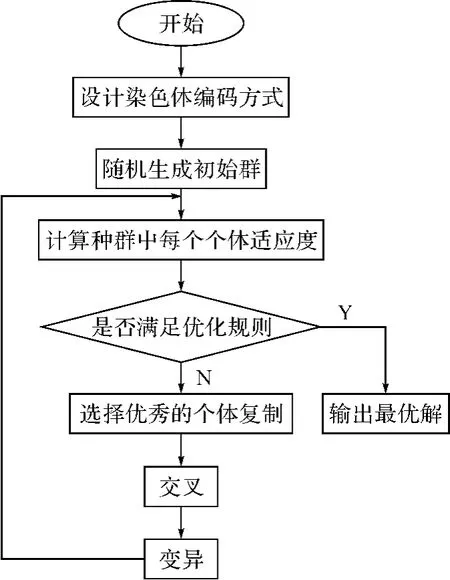
图2 GA流程图
其中μi=2,βi=3,mi(i=1,2,3,4,5)取整数.
上面优化问题实际上是连续变量和离散变量并存的混合非线性规划问题.
系统其余各参数值如表1所示:

表1 冗余元件与可选设计数据表
根据上述步骤编写求解问题的Matlab部分代码如下:
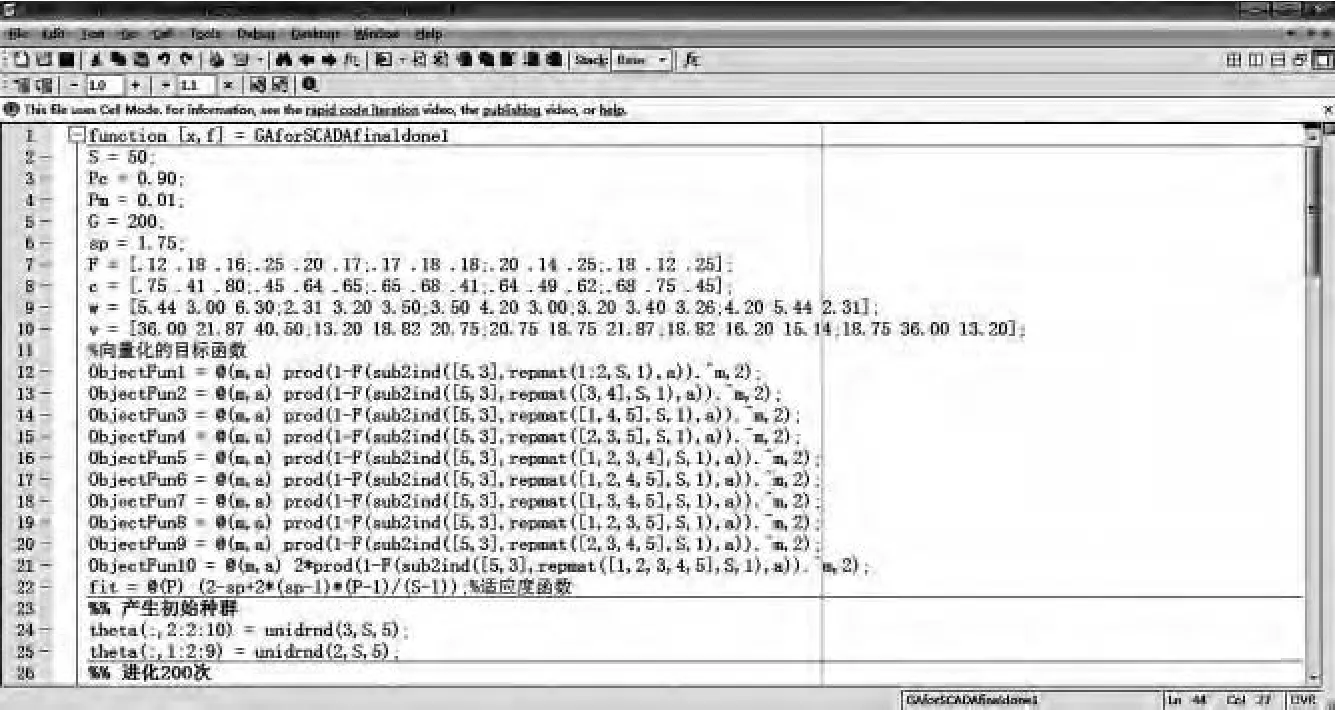
经过运行可以得到进化过程中200代每一代的最优个体和相应的系统适应度函数f.运行结果为:

经过多次运行,发现寻优比较稳定,基本上每次都能得到如下最优解:
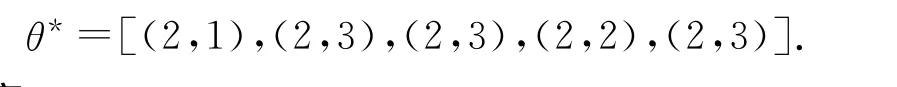
上述解对应表2所列内容.
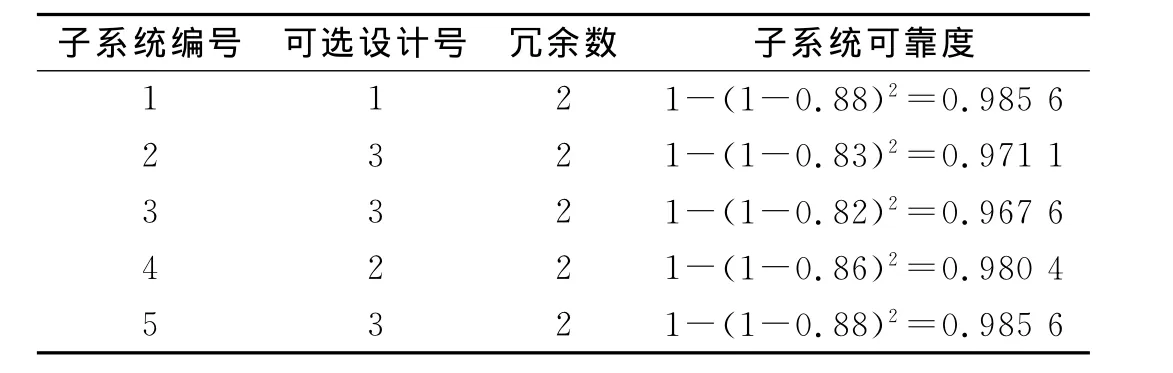
表2 θ*对应的可选设计和冗余度分配表
将各子系统的可靠度代入(3)式,则得到整个系统的可靠度5.5万元≤5.8万元.
经过Matlab运算可得到
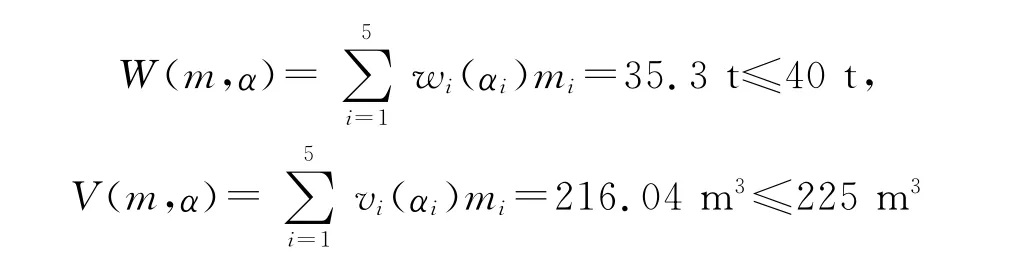
均满足限制条件.
同时,与表2数据一致的遗传算法进程中的迭代次数同系统可靠度之间的变化曲线如图3所示.
由图3可以看出,进化过程中200代,系统可靠度逐渐增大,直到达到最优解R(θ*)=0.998 9时趋于稳定.由于遗传算法的随机性,每次运行曲线不会完全一样,但是绝大多数都会最终达到最优解.

图3 迭代次数同系统可靠度曲线
4 结语
在造价、体积和重量约束条件下,桥式网络系统的可靠性优化问题是一个具有对于大规模的、多峰多态函数、非线性的的全局性混合优化问题.相比较文献[2,5]中的算法,Matlab的BNB20()函数和LINGO软件只能解决一些相对简单的系统优化,而遗传算法提供了一种求解大型复杂系统优化问题的通用框架,它不依赖于问题的具体领域,有很强的鲁棒性.本文中提出建立子系统可靠度指标和冗余个数一体化并发设计问题,建立带有可选设计α的桥式网络系统可靠度和冗余度分配优化模型,此模型更贴近实际生产的网络系统.最后给出算例,通过遗传算法进对系统的可靠度和冗余度进行分配优化,为实际问题中的网络系统提供设计方法,对提高各种网络系统的可靠度、降低成本有重要的意义.
[1]曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006.
[2]蒋仁言.可靠性模型与应用[M].北京:机械工业出版社,1999.
[3]赵东方.数学建模与计算[M].北京:科学出版社,2007.
[4]Way Kuo,Rajendra Prasad V,Frank A,et al.最优可靠性设计:基础与应用[M].郭进利,阎春宁,译.北京:科学出版社,2011.
[5]徐玖平,胡知能.运筹学——数据·模型·决策[M].北京:科学出版社,2006.
[6]段平,胡捷.基于 MATLAB的串联系统可靠性整数优化[J].信息与电子工程,2009,7(5):477-479.
[7]杨帆,郝建春.基于改进遗传算法的系统可靠性分配优化[J].机械设计与制造,2013(2):201-203.
[8]孔德剑.基于改进的遗传算法的多目标优化问题研究[J].计算机仿真,2012,29(2):213-215.
[9]张洪洛,张振友,田凤明.装备系统可靠性分配冗余最优化方法[J].四川兵工学报,2012,31(11):48-49.
[10]Kang Won Hee,Song Junho,Gardoni Paolo.Matrix-based system reliability method and applications to bridge networks[J].Reliability Engineering and System Safety,2008,93(11):1584-1593.
[11]Chuan Hsin-Kuo,Lin Hai-Ching.A directed genetic algorithm for global optimization[J].Applied Mathematics and Computation,2013,219(14):7348-7364.
[12]边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,27(7):2425-2429.
[13]袁宏伟.基于遗传算法的计算机网络可靠度优化计算[J].计算机光盘与应用,2012,23:6-8,32.
[14]吴鹏.MATLAB高效编程技巧与应用:25个案例分析[M].北京:北京航空航天大学出版社,2010.
[15]曹素功,唐世江,肖新强,等.南平樟湖库区大桥钢浮箱设计[EB/OL].中国科技论文在线,2013-02-05.

