TTF-CA有机分子晶体多铁性的数值研究
杨敏,黄忠兵
(湖北大学物理与电子科学学院,湖北 武汉430062)
0 引言
近年来,多铁材料(具有磁性和铁电性共存的单相材料)的研究成为一个热门研究课题[1].许多新型多铁材料已经被发现,相关的实验和理论研究对其晶体结构和多铁性产生的机理作了大量的探讨[2-4].但是常见的多铁材料一般都是过渡金属复合物,具有很强的自旋、晶格、以及电荷自由度之间的相互作用,对澄清相关物理特性造成很大的困难.有机分子晶体材料由于其重量轻、可塑性强、无毒、以及丰富的物性等优点一直受到广泛的关注,而有机多铁材料的探寻正在成为一个新的研究方向.通过电导、介电常数、以及电极化等特性的实验研究,Lunkenheimer等人在有机电荷转移盐(BEDT-TTF)2Cu[N(CN)2]Cl中发现了反铁磁和电荷序诱导的铁电性的共存状态[5].Thomas等人基于密度矩阵重整化群计算预言在融合甘菊蓝(azulene)中存在铁电和铁磁共存的室温多铁性特征[6].Giovannetti等人采用第一性原理和Hartree-Fock平均场理论相结合的方法探讨了TTF-CA分子晶体中的多铁性特征[7].此外,Giovannetti等人还结合第一性原理和量子多体方法研究了TMTTF2-X(tetramethyltetrathiafulvalene)2-X)中的多铁性特征[8].最近,华中科技大学姚凯伦教授领导的研究小组基于派尔斯-自旋模型分析了TTF-BA(tetrathiafulvalene-p-bromanil)有机量子磁体中电极化转变和磁电耦合行为以及各向异性磁相互作用的物理效应[9].虽然人们在有机多铁性领域开展了一些研究工作,但是与过渡金属复合物多铁材料类似,有机分子晶体中自旋、晶格以及电荷自由度之间的相互作用对其磁电耦合具有关键影响,同时给理论研究带来很大的困难,因而结合各种先进的方法进行综合研究可以更准确地理解有机多铁材料的复杂物性.本文中,我们将超越Giovannetti等人采用的平均场近似,利用数值计算方法能严格处理电子关联这一优势深入探讨TTF-CA分子晶体在电子半填充和偏离半填充时的多铁性特征.
TTF-CA是一种电荷转移化学盐类,并由施主(TTF)和受主(CA)分子交替堆排而成,见图1所示.由于它具有典型的中性-离子性转变特性,近几十年来倍受关注.在常压下,TTF-CA在温度约81 K时发生一 级 中 性-离 子 性 相 变[10-12],晶 体 由P121/n1中心对称群的中性态转变为P1n1非中心对称群的离子态[13].晶体对称性的破坏改变了同一平面内TTF和CA分子的位置,并导致沿堆排轴a长短键的形成,从而出现了二聚化的形成.这种二聚化特征在材料的介电响应实验中得到清晰的体现,具体现象是伴随着在一级中性-离子性相变发生了一级铁电相变[14-15].
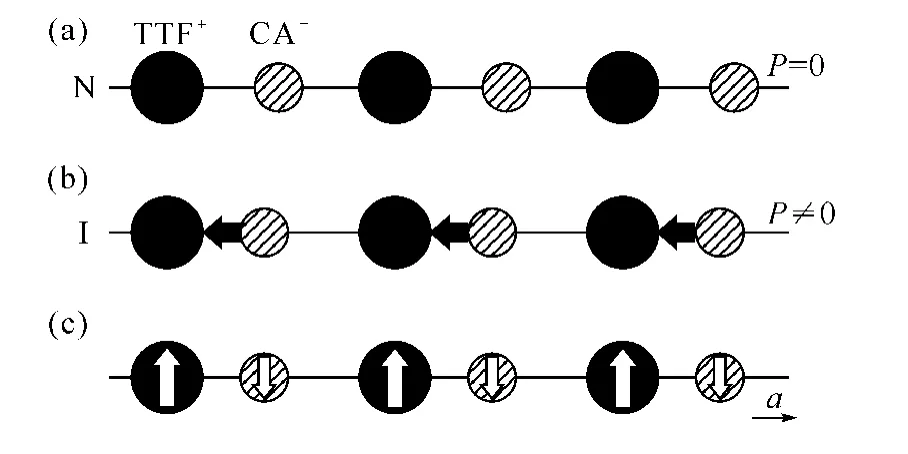
图1 TTF和CA分子沿堆排轴a的分布示意图
1 计算方法
为了理解TTF-CA的晶体结构和铁电相变机理,我们采用一维派尔斯-哈伯德模型描述TTF和CA分子上相互作用的多电子体系[16-19],其哈密顿量为:
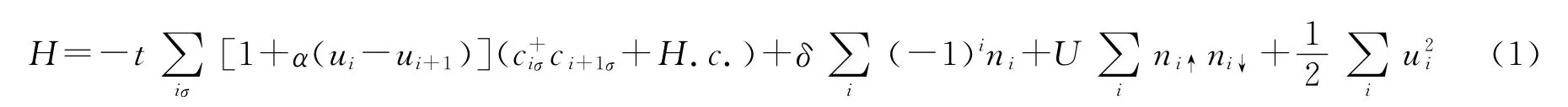
第一项表示近邻格点之间(即TTF和CA之间)的电子跃迁运动,第二项是代表TTF和CA分子不同的离子势能,第三项是上下自旋电子占据同一格点产生的库仑相互作用能量,第四项是格点偏离平衡位置的势能.这里ciσ代表格点i上自旋状态为σ电子的湮灭算符;t代表电子跳跃强度;ui为描述TTF和CA离子偏移平衡位置的形变参数;电声子耦合系数为α,δ代表TTF和CA分子的离子势能强度;U代表在位库仑相互作用强度.
在零温和给定电子数的情况下,哈密顿式(1)中的多电子基态波函数可由数值精确对角化[20]和约束路径量子蒙特卡罗方法[21]严格得到,然后可以计算基态能量和格电电子占据数、磁矩以及格点之间的自旋关联等物理量.形变参数ui通过基态能量作为ui函数的极低值加以确定.当晶格处于未形变状态时,ui=0,而当晶格处于二聚化状态时,ui=(-1)iu0.在数值精确对角化方法中,由于多电子构成的希尔伯特空间随格点数指数增加,该方法主要用以计算10个和14个格点的系统.采用Hartree-Fock近似方法,式(1)改写为以下形式:式(2)中的单电子哈密顿量可以通过自洽方法加以求解,当自洽收敛后得到体系的近似基态波函数(由单个斯莱特行列式表示).

2 计算结果与讨论
通过拟合第一性原理得到的能带结构,可以导出近邻电子跃迁强度t=0.2 e V,δ=0.06 eV[22-23].我们选取参数范围U=0 t~8 t,其包含了从弱电子关联U=0 t~2 t到强电子关联U>4 t(4 t为能带的宽度)的整个区间.电声子耦合系数为α取值为0.0~0.8,包含了从弱电声子相互作用到强电声子相互作用的整个范围.下列图中和表格中的能量E和库仑相互作用U均以t为单位.
我们首先讨论当填充电子数与格点数相同即半填充情况下的计算结果.图2和图3分别描述10个格点的一维链在U=0 t~8 t,α=0.0~0.8这一参数空间内,系统基态的二聚化参数u0和近邻格点间沿z方向的自旋关联函数〈SziSzj〉.图2中随着颜色的变浅,二聚化逐渐增大,其中黑色区间和灰色区间的交界区表示从未形变态到二聚化态之间的相边界;图3中随着颜色的加深,近邻格点间自旋关联增强,即系统反铁磁性增强.从图2可以发现当α取大于0.2的某个值(具体数值依赖于U)时,系统处于二聚化状态,从而可以表现出铁电性.图2中白色曲线是根据式(2)中Hartree-Fock平均场近似得到的相边界.可以明显看出,当U<2 t时,数值精确化给出的结果与平均场给出的结果符合非常好.物理原因是当电子关联较弱时,系统内的量子涨落较小,平均场近似能够较为准确地描述系统的物理特性.但是当U>2 t时,数值计算的相边界显著低于平均场给出的相边界,尤其是当U大于带宽4 t时.该结果不仅修正了平均场的相边界,而且表明对处于强电子关联的有机分子晶体,即使较弱的电声子相互作用也可以导致系统出现铁电特性.从图3可以发现当U较大且系统处于二聚化状态时(U>2 t,α>0.2),近邻格点间自旋关联较强.图2和图3中的结果说明具有较强电子关联和电声子相互作用的分子晶体易于表现出多铁性.
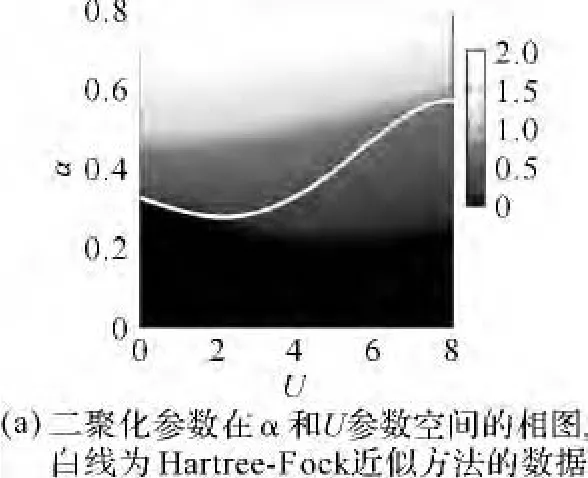
图2 二聚化参数在α和U参数空间的相图,白线为Hartree-Fock近似方法的数据

图3 近邻自旋关联函数〈Szi S zj〉在α和U参数空间的相图
表1给出了数值精确对角化方法得到的10个格点和14个格点系统相边界对比数据,其中αc表示从未形变态到二聚化态转变的电声子耦合系数.当U=0.0 t和1.0 t时,两个系统的相变界符合很好,而当U取更大值时,14个格点系统的相边界略低于10个格点系统的结果.

表1 具有10个格点和14个格点系统相边界的对比数据
为了进一步检验数值精确对角化得到的相边界,我们采用约束路径量子蒙特卡罗方法对具有30个格点和42个格点的系统进行了计算.图4表示U分别为1.0 t、2.0 t和4.0 t时,具有30个格点的系统总能量E随二聚化参数u0的演化曲线,图中不同的符号代表不同的电声子耦合系数α.从图4(a)~(c)中可以发现当U取值为1.0 t、2.0 t和4.0 t时,相边界对应的α分别约为0.30、0.25和0.20.该结果与14个格点系统的结果符合很好,证明随着尺寸的增加,相变边界点趋于稳定存在于某一固定范围之内,因而我们的数值结果定量地反映了一维分子链的物理行为.
当电子数为半填充时,我们发现系统总是处于总自旋为零的反铁磁状态,一个重要的问题是当电子数偏离半填充时,系统能否表现出铁磁与铁电极化共存的多铁状态?图5显示了10个格点和14个格点系统当电子数比半填充分别少2个和4个电子时总能量随二聚化参数u0的演化行为.图中给出了沿z方向总自旋Sz为0和1的计算结果,Ne代表填充电子数.我们发现当电子数比半填充少2个电子时,两个系统均表现出二聚化特征,而且不同Sz的曲线重合在一起,说明系统基态为总自旋S=1的自旋极化(即未饱和铁磁)状态.该结果说明当电子数略低于半填充时,系统具有铁磁与铁电极化共存的多铁性状态.当电子数比半填充少4个电子时,系统总能量随u0单调上升,说明未形变状态为基态,从而不具有铁电性.二聚化产生的条件是费米波矢kF靠近±π/2,而当电子数偏离半填充较大时(例如少4个电子的情况),对应的费米波矢距离±π/2较远,因而难以通过形成二聚化态来降低系统总能量.

图4 具有30个格点的一维链总能量随二聚化参数u0的演化行为
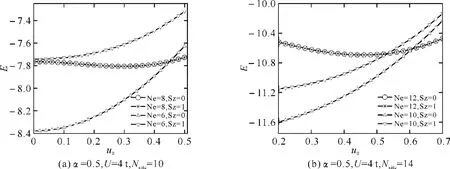
图5 10个格点(a)和14个格点(b)系统当电子数
3 结 论
我们基于一维派尔斯-哈伯德模型,采用数值精确对角化和约束路径量子蒙特卡罗数值方法研究了有机分子晶体TTF-CA的多铁性特征.当电子数处于半填充时,数值模拟结果证实当电声子相互作用超过一定的临界值且在位库仑相互作用U处于中等至强关联区间时,分子晶体内存在反铁磁和铁电极化共存的多铁状态,而且数值结果预言多铁性产生的电声子相互作用强度远低于平均场给出的结果.当电子数略低于半填充时,体系存在铁磁与铁电极化共存的多铁性状态,但是偏离半填充较大时,系统处于未形变的基态,从而难以形成多铁性状态.我们超越平均场的计算结果不仅加深了对TTF-CA多铁性产生的微观机理的理解,而且为寻找铁磁与铁电极化共存有机多铁性材料提供了思路.
[1]Spaldin N A,Fiebig M.The renaissance of magnetoelectric multiferroics[J].Science,2005,309:391-392.
[2]Eerenstein W,Mathur N D,Scott J F.Multiferroic and magnetoelectric materials[J].Nature(London),2006,442:759-766.
[3]Cheong S W,Mostovoy M.Multiferroics:a magnetic twist for ferroelectricity[J].Nature Materials,2007(6):13-20.
[4]Picozzi S,Yamauchi K,Sanyal B,et al.Dual nature of improper ferroelectricity in a magnetoelectric multiferroic[J].Phys Rev Lett,2007,99:227201.
[5]Lunkenheimer P,Müller J,Krohns S,et al.Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism[J].Nature Materials,2012,11:755-758.
[6]Thomas S,Ramasesha S,Hallberg K,et al.Fused azulenes as possible organic multiferroics[J].Phys Rev B,2012,86:180403(R).
[7]Giovannetti G,Kumar S,Stroppa A,et al.Multiferroicity in TTF-CA origanic molecular crystals predicted through ab initio calculations[J].Phys Rev Lett,2009,103:266401.
[8]Giovannetti G,Kumar S,Pouget J P,et al.Unraveling the polar state in TMTTF2-PF6 organic crystals[J].Phys Rev B,2012,85:205146.
[9]Wang S,Li R,Fu H H,et al.A theoretical model for anisotropic multiferroics[J].Appl Phys Lett,2013,103:132911.
[10]Horiuchi S,Tokura Y.Organic ferroelectrics[J].Nature Materials,2008(7):357-366.
[11]Torrance J B,Girlando A,Mayerle J J,et al.Anomalous nature of neutral-to-ionic phase transition in tetrathiafulvalene-chloranil[J].Phys Rev Lett,1981,47:1747.
[12]Lemée-Cailleau M H,Le Cointe M,Cailleau H,et al.Thermodynamics of the neutral-to-ionic transition as condensation and crystallization of charge-transfer excitations[J].Phys Rev Lett,1997,79:1690.
[13]Le Cointe M,Lemée-Cailleau M H,Cailleau H,et al.Symmetry breaking and structural changes at the neutral-toionic transition in tetrathiafulvalene-p-chloranil[J].Phys Rev B,1995,51:3374.
[14]Okamoto H,Mitani T,Tokura Y,et al.Anomalous dielectric response in tetrathiafulvalene-p-chloranil as observed in temperature-and pressure-induced neutral-to-ionic phase transition[J].Phys Rev B,1991,43:8224.
[15]Soos Z G,Bewick S A,Peri A,et al.Dielectric response of modified Hubbard models with neutral-ionic and Peierls transitions[J].J Chem Phys,2004,120:6712-20.
[16]Nagaosa N,Takimoto J.Theory of neutral-ionic transition in organic crystals Monte Carlo simulation of modified Hubbard model[J].J Phys Soc Jpn,1986,55:2735.
[17]Freo Del L,Painelli A,Soos Z G.Giant infrared intensity of the Peierls mode at the neutral-ionic phase transition[J].Phys Rev B,2002,89:027402.
[18]Tsuchiizu M,Furusaki A.Ground-state phase diagram of the one-dimensional half-filled extended Hubbard model[J].Phys Rev B,2004,69:035103.
[19]Painelli A,Girlando A.Zero-temperature phase diagram of mixed-stack charge-transfer crystals[J].Phys Rev B,1988,37:5748.
[20]Lin H Q,Gubernatis J E.Exact diagonalization methods for quantum systems[J].Computers in Physics,1993,7(4):400.
[21]Zhang S W,Carlson J,Gubernatis J E.Constrained path Monte Carlo method for fermion ground states[J].Phys Rev B,1997,55:7464.
[22]Katan C,Koenig C,Blöchl P E.Ab-initio calculations of one-dimensional band structures of mixed-stack molecular crystals[J].Solid State Commun,1997,102:589-594.
[23]Oison V,Katan C,Rabiller P,et al.Neutral-ionic phase transition:a thorough ab initio study of TTF-CA[J].Phys Rev B,2003,67:035120.

